太赫兹在高速率通信、高分辨率雷达和成像等方面的应用和发展，迫切需要性能稳定的大功率太赫兹辐射源。微电真空折叠波导行波管是太赫兹低端高功率太赫兹辐射源的优选器件，其功率、带宽和散热等综合性能优于同类器件，结构紧凑、性能稳定，而且基于现有的加工工艺，具有可实现性，可用于0.1~1 THz频段高功率太赫兹辐射的产生。尤其把先进的微加工技术和真空电子技术有效结合起来，能够大大促进器件的发展，使器件的工作频率更高、体积更小、重量更轻和成本更低^[1-3]。目前，对太赫兹折叠波导行波管的研究工作仍然具有很多关键技术需要攻关，加工工艺、测试手段、理论的实验验证等仍在不断进步，工作性能不断提升，工作频率从低波段向更高波段推进。慢波结构(即高频结构)是整个行波管的核心部件，它通过束-波互作用机理，把电子注的能量转化为电磁场的能量，对行波管的工作频率、带宽、输出功率、增益和效率等参数起着决定性的作用^[4-7]。人们也在不断探索新的慢波结构构型，寻求更佳的输出性能或更好的可实现性^[8-10]。本文提出一种大功率、高增益、紧凑型折叠波导慢波结构，该慢波结构采用变参数分段化设计，持续保持束-波“同步”共振，增加束-波互作用长度，进一步将俘获电子的能量转化为太赫兹波，从而提升束-波能量转化效率以及器件输出功率。

1.   分段变参数折叠波导慢波结构的构思

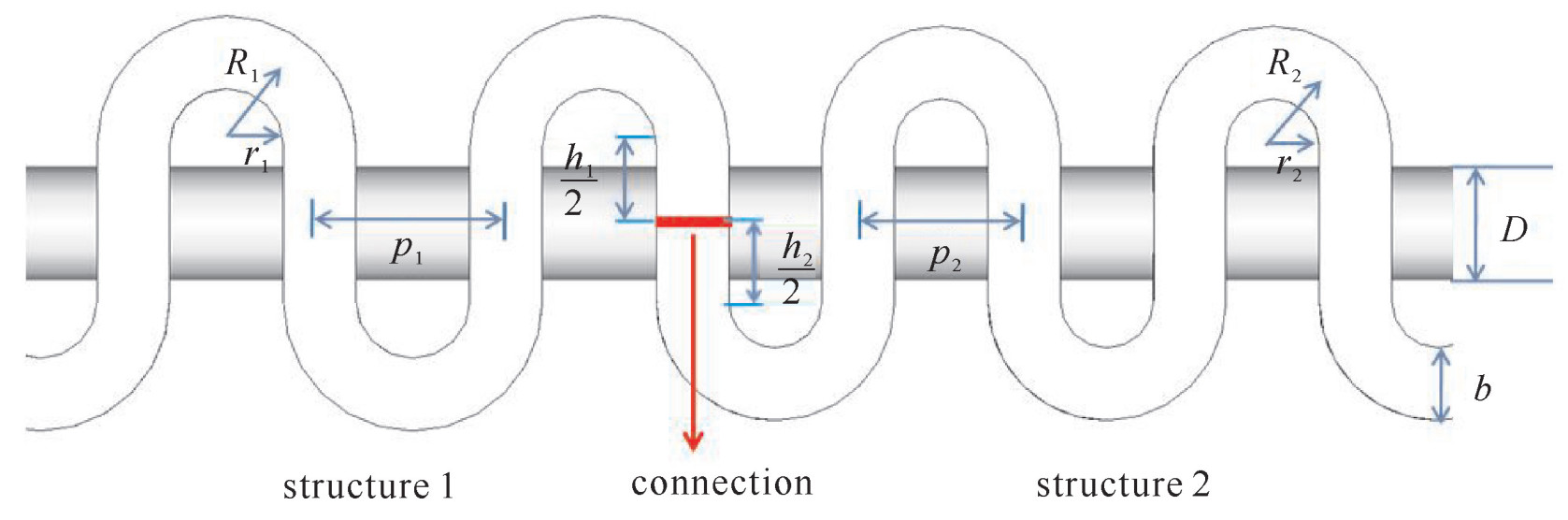
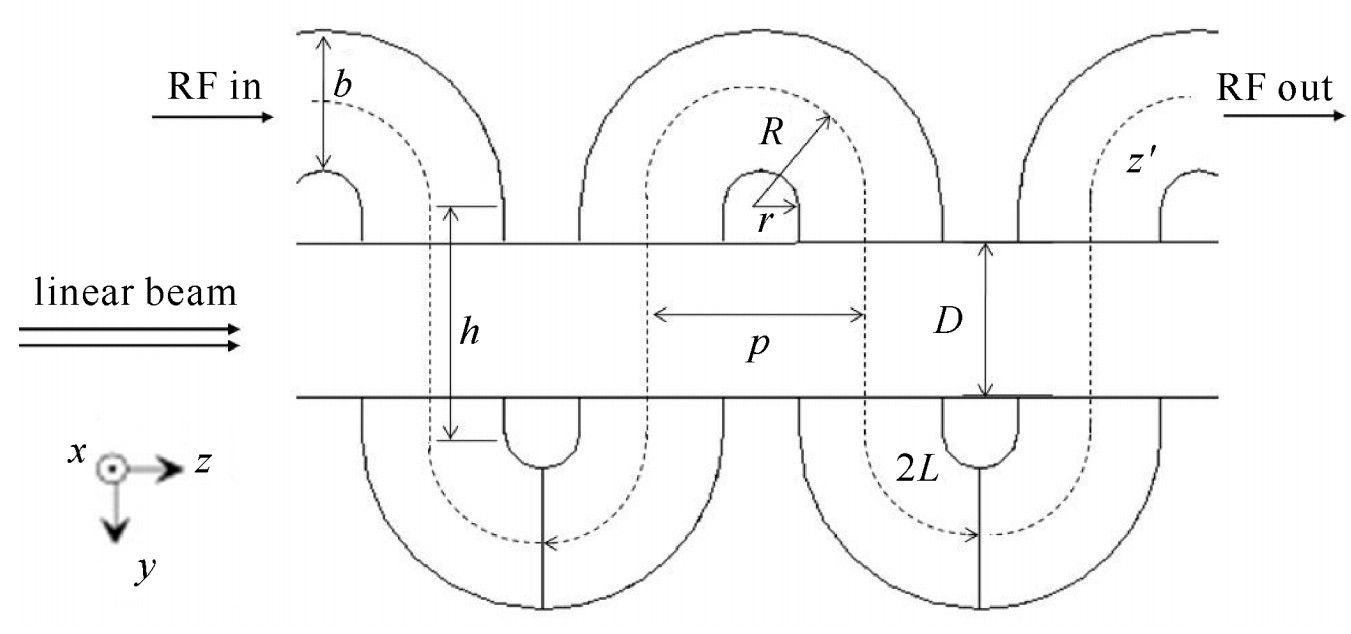
传统均匀型折叠波导慢波结构如图 1所示，a为矩形波导的长边，b为矩形波导的短边，p为慢波结构沿z方向的半周期长度，h为慢波结构的直波导段长度，L为折叠波导的半周期长度，L=h+πp/2。

图  1  折叠波导慢波结构

Figure  1.  Folded waveguide slow wave structure

下载: 全尺寸图片 幻灯片

折叠波导慢波结构的折叠度可表示为

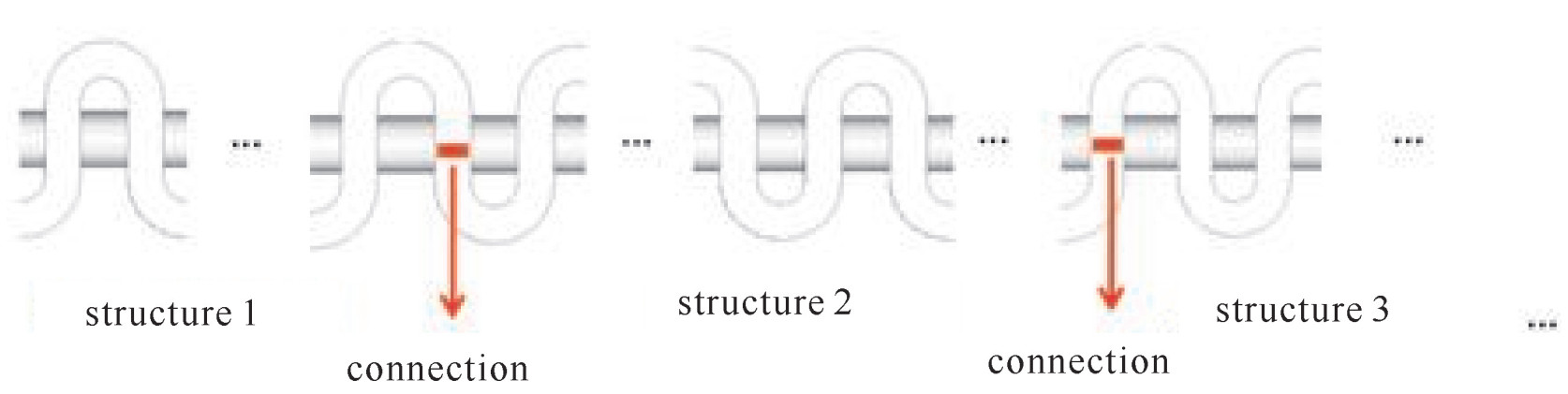
本文提出的分段式折叠波导结构，可以由两个或两个以上的慢波结构相联组成，其折叠度依次增大，即g₁ < g₂ < g₃…，满足$\frac{v_2}{v_1}=\frac{g_1}{g_2}, \frac{v_3}{v_2}=\frac{g_2}{g_3} \cdots$，其中v_i为慢波结构i的入口处被电磁场俘获的电子束团的平均速度。各段慢波结构折叠度可以通过调整几何参数p或h来实现。对于波导宽边a、窄边b、电子束孔径D等物理量，前后各段慢波结构相同。分段式慢波结构前后两段的结合处是在直波导处，取前后两段慢波结构各自一半的直波导无缝连接，如图 2所示。

图  2  多段式折叠波导慢波结构示意图

Figure  2.  Multistage folded waveguide slow wave structure

下载: 全尺寸图片 幻灯片

2.   小信号理论

折叠波导慢波结构的小信号增益方程可表示为

式中：$k_{z n}=\frac{(2 n+1) \pi}{p}+\frac{L}{p} \sqrt{\frac{\omega^2-\omega_c^2}{c^2}}-\delta k=\frac{(2 n+1) \pi}{p}+k_{z 01}^{\circ}-\delta k=k_{z n}^{\circ}-\delta k$，k_zn是慢波结构z方向n次谐波波数，$k_{z 01}^{\circ}=\frac{L}{p} \sqrt{\frac{\omega^2-\omega_c^2}{c^2}}, k_{z n}^{\circ}=\frac{(2 n+1) \pi}{p}+k_{z 01}^{\circ}$，δk是束波互作用引起的增量；$\bar{k}=\frac{k}{k_{\mathrm{c}}}, \bar{\omega}=\frac{\omega}{\omega_{\mathrm{c}}}, c=\frac{\omega_{\mathrm{c}}}{k_{\mathrm{c}}}$，k为波数, ω为角频率, ω_c为截止角频率，k_c为横向角波数；γ₀为相对论因子，$\beta_{z 0}=\frac{v_{z 0}}{c}$，v_z0为电子初速度，c为光速；ε为介电常数；e为电子电量；m₀为电子质量；I_o为电子注电流；$C_{\mathrm{b}}=\frac{1}{A_{\mathrm{b}}} \int_{S_{\mathrm{b}}}\left[\sin \left(\frac{\pi}{a} x\right)\right]^2 \mathrm{~d} S$, A_b为电子注横截面面积, S_b为电子注所在横截面面积；$G_{\mathrm{m}}=\frac{\sin \left(k_{z n} \frac{b}{2}\right)}{k_{z n} \frac{b}{2}}$为间隙因子^[11-13]。

z方向电磁波场的增长量为e^j(δk)z，则功率的线性增长率(即小信号增益)可以表示为

3.   两段式折叠波导慢波结构的设计实现和数值模拟验证

基于小信号理论，进行了0.345 THz两段式折叠波导慢波结构参数的理论设计和数值模拟验证。两段式折叠波导慢波结构的尺寸参数如图 3所示。

图  3  两段式折叠波导慢波结构的尺寸参数示意图

Figure  3.  Size parameters of two stages of folded waveguide slow wave structure

下载: 全尺寸图片 幻灯片

3.1   第一段慢波结构的设计

采用小信号理论和数值模拟，优化选取了首段慢波结构的参数，如表 1所示，其中小信号理论设计的共振电压和数值模拟采用的共振电压略有差别，小信号理论设计的共振电压为17.0 kV，而数值模拟优化得到的共振电压为18.6 kV，存在偏差主要因为电子注导通管的开孔及其大小会引起束-波互作用的共振点偏移，小信号理论计算中未考虑该因素，而在建模和仿真中考虑了该因素。电子枪与首段慢波结构对接，因此电子枪产生的束流参数应与首段慢波结构束-波互作用所需电子注参数相匹配。

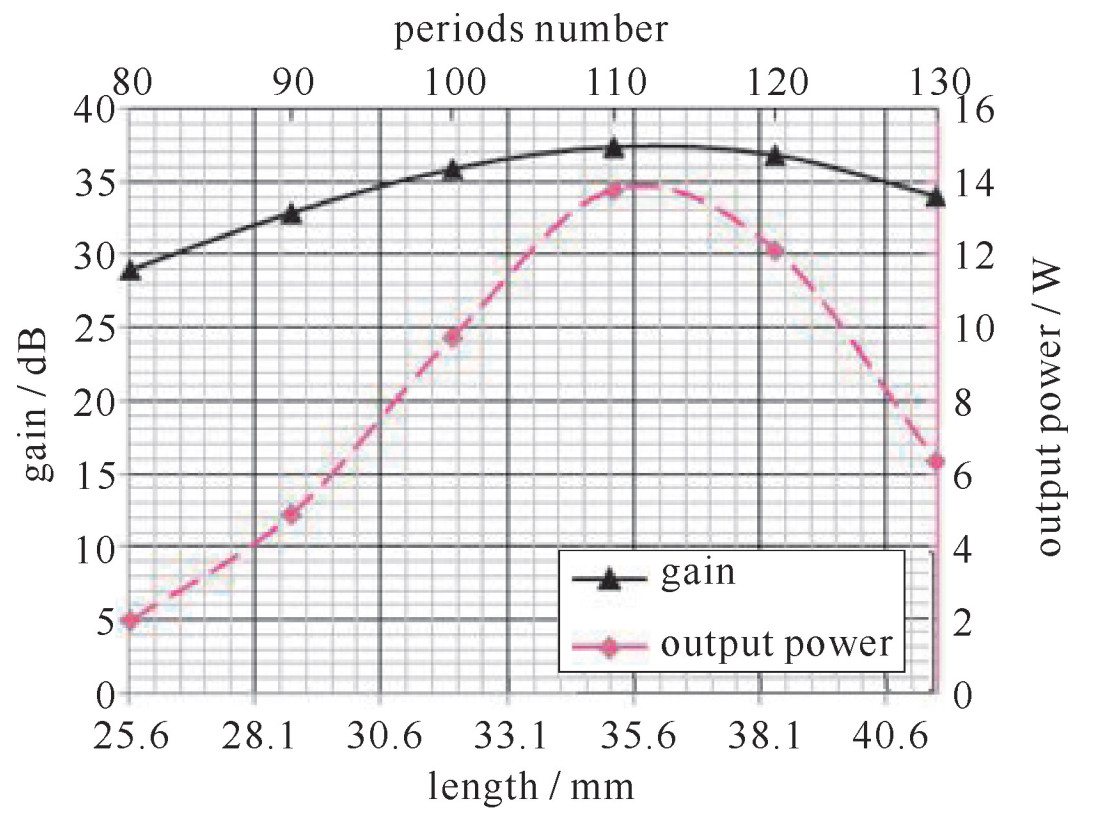
表  1  传统均匀型慢波结构模型参数

Table  1.  Parameters of traditional folded waveguide slow wave structure

a1/mm	b1/mm	p1/mm	h1/mm	D1/mm	beam voltage/kV
0.49	0.085	0.16	0.15	0.10	17.0(18.6)

下载: 导出CSV 

| 显示表格

首段慢波结构的截断长度以及首段输出端被俘获电子束团的平均速度是两段式慢波结构设计的关键，直接决定着第二段慢波结构的参数设计。对首段折叠波导慢波结构工作特性进行了三维PIC数值模拟，得到增益和输出功率随束-波互作用长度或周期数的变化规律，如图 4所示，可以看出，增益随慢波结构长度的增长呈现先增后减的趋势，在束-波互作用长度为110周期(即为35.2mm)时增益达到最大，即为增益饱和点。

图  4  增益和输出功率随束-波互作用长度以及周期数目变化趋势

Figure  4.  Gain and output power vs beam-wave interaction length and SWS periods

下载: 全尺寸图片 幻灯片

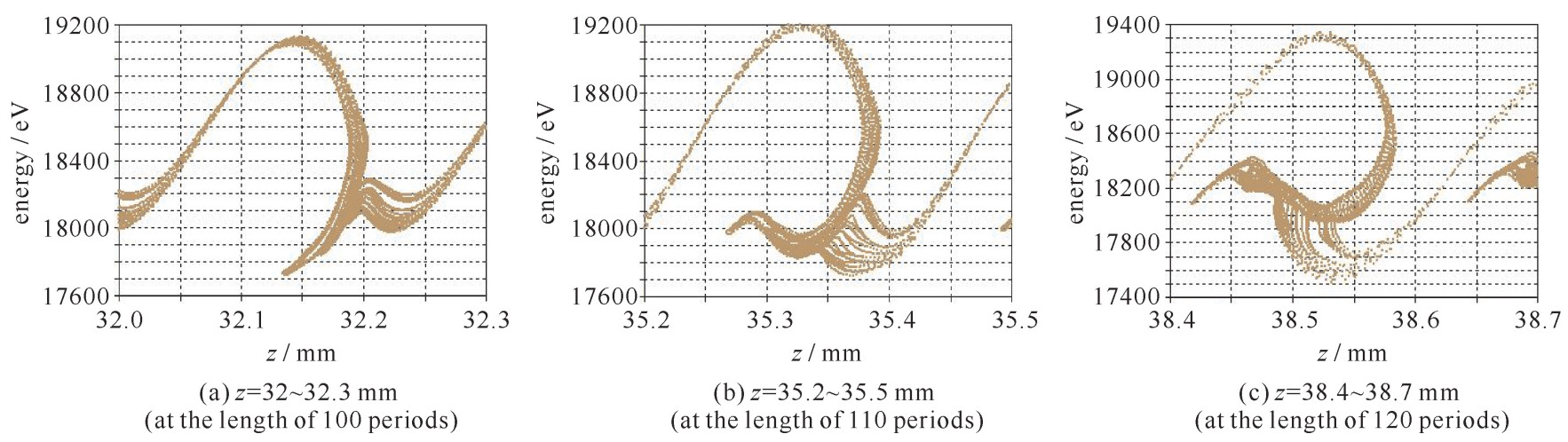
数值模拟得到电子注能量相空间调制图，图 5(a)~(c)展示了电子注在100，110，120个周期处一个波长范围内电子注的调制情况以及能量动态变化，得到结论：(1)初始电子注能量集中在18.6 kV附近，随着束-波互作用的进行，电子出现速度调制和群聚，把能量交付给太赫兹波，自身整体平均能量不断降低，在110个周期处电子整体平均能量达到最低，大部分电子能量分布在17.8~18.1 kV范围内；(2)在120个周期附近，电子平均能量相对于110个周期时增大，大部分电子能量分布在17.9~18.4 kV范围内，此时电子从电磁场中索取能量，导致输出功率相比于110个周期时有所下降。

图  5  不同轴向位置处1 THz波长范围内的电子注调制情况及其能量分布

Figure  5.  Electron beam's modulation and energy distribution in 1 THz wavelength at different axial positions

下载: 全尺寸图片 幻灯片

经上述分析，第一段慢波结构的长度截断点应该选择在增益饱和点之前，通过观察图 4~8，决定第一段慢波结构选取100个周期(即长度为32 mm)比较合适，此时电子大部分电子能量集中在18.0~18.3 kV之间。

图  6  小信号增益曲线

Figure  6.  Small signal gain curves

下载: 全尺寸图片 幻灯片

图  7  输出功率随慢波结构长度的关系

Figure  7.  Output power vs SWS length

下载: 全尺寸图片 幻灯片

图  8  两段式慢波结构不同轴向位置处1 THz波长范围内的电子注调制情况及其能量分布

Figure  8.  Electron beam's modulation and energy distribution in one terahertz wavelengths at different axial positions for two stage slow wave structure

下载: 全尺寸图片 幻灯片

3.2   第二段慢波结构的参数设计和仿真验证

第一段慢波结构输出的电子束能量决定着第二段慢波结构的参数设计。第二段慢波结构的波导宽边a₂、窄边b₂、电子束孔径D₂等物理量和首段相应参数取值相同，本节通过调整几何参数p，把电子束和电磁波调整到“共振”高效换能状态，从而使得束波互作用持续有效进行。

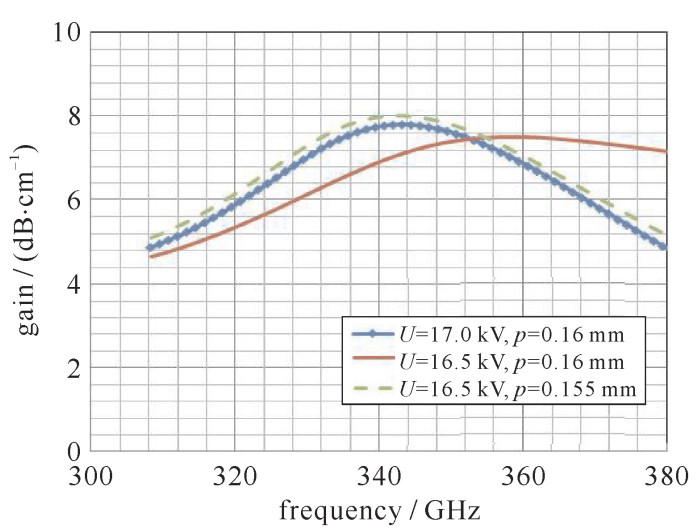
通过理论计算，获得参数p的变化对小信号增益曲线的中心频点的影响规律，实现了参数p的选取。如图 6所示，随着束-波互作用的进行，电子能量降低，假设电子能量从17.0 kV下降到16.5 kV，小信号增益曲线右移，通过调整结构参数p移动小信号增益曲线，从而把中心频点拉回工作频点0.345 THz，并取得较高的增益。

基于小信号理论分析，选取了第二段慢波结构参数p₂，其他结构参数和第一段慢波结构一致，如表 2所示。

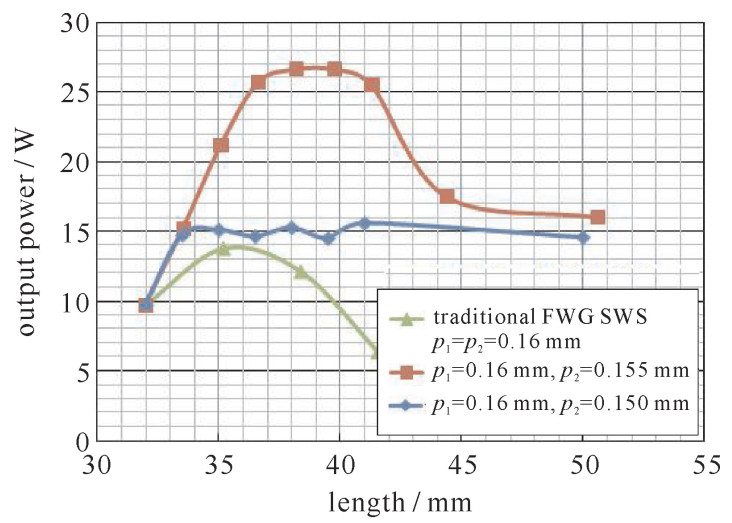
表  2  第二段折叠波导慢波结构参数

Table  2.  Parameters of the second section of folded waveguide slow wave structure

a2/mm	b2/mm	p2/mm	h2/mm	D2/mm
0.49	0.085	0.155(0.15)	0.15	0.10

下载: 导出CSV 

| 显示表格

通过数值模拟，得到p₂为0.155 mm和0.15 mm时，两段式慢波结构的输出功率和增益随慢波结构总长度的变化关系，结果如图 7所示，可以看出：p₂=0.155 mm时慢波结构输出最大功率和饱和增益较好，与传统均匀型慢波结构对比，相同长度下，两段式慢波结构的功率(增益)远大于传统均匀型慢波结构的功率(增益)，在饱和点处，两段式慢波结构的功率为26.6 W，电子效率为9.53%，相对于传统均匀型慢波结构饱和点功率(13.7 W)和电子效率(4.91%)，饱和点功率和电子效率均提高了94%。

图 8展示了第二段慢波结构长度在20，25个周期处一个波长范围内电子注的调制情况以及能量动态变化，可以看出，随着第二段慢波结构中束波互作用的进行，电子注整体平均能量进一步持续拉低，在第二段慢波结构为25个周期处，主要束团的能量分布在16.6~17.2 kV范围内，相对于首段慢波结构100个周期处(18.0~18.3 kV)，主要电子注团的能量下降幅度非常大，因此器件功率或增益得到大幅度提升。

4.   结论

本文提出折叠波导慢波结构采用分段化设计提高器件增益的新构想。结合小信号理论分析和束波互作用的三维PIC数值模拟，给出该新型结构理论设计方法，并进行了设计实现和模拟验证。0.345 THz两段式折叠波导慢波结构验证表明：在相同电功率输入和同等器件尺寸条件下，分段变参数型慢波结构得到的饱和点功率(26.6W)和电子效率(9.53%)，相对于传统均匀型慢波结构饱和点功率(13.7W)和电子效率(4.91%)，都提高了94%，证明了两段式慢波结构的巨大优势，并且可以推广到多段式，只要采用分段变参数结构有效控制被俘获电子束团的能量，就可进一步提高器件的电子效率和功率。