Volume Bragg grating filters and its spectral imaging application
-
摘要: 利用厚体布拉格光栅的波长选择特性对目标光场进行窄带滤波，是实现高光谱成像的一种新途径。基于严格耦合波理论，设计了体布拉格光栅结构，探索了厚体布拉格光栅的制作工艺，搭建系统光路验证了体布拉格光栅的光谱成像能力。研究结果表明：要获得较窄滤波谱宽，需要提高体布拉格光栅的厚度周期比，并严格控制入射光束发散角；刻写光束质量、震动和偏振会极大地影响制作的光栅条纹面质量，需要从优化写入光的光束均匀性、采用防震措施以及调整两刻写光束偏振一致性等方面优化刻写过程，以提高光栅的衍射效率和质量；验证了体布拉格光栅滤波片进行空间二维面阵成像的能力，宽谱光源透射条件下，通过对入射光束进行准直，滤波谱宽5 nm左右，空间分辨率约4 lines/mm；漫反射条件下，使用体布拉格光栅对进行色散补偿，能够实现较为清晰的成像，空间分辨率约4.9 lines/mm。Abstract: It is a new path to achieve hyperspectral imaging of objective area by employing the wavelength selectivity of thick volume Bragg gratings(VBGs). Based on the rigorous coupled wave theory, grating structures were optimally designed, fabricating craft were explored, the imaging system was constructed and the imaging ability of the VBG was verified. The results showed that: to obtain narrow filtered bandpass, we should improve the ratio of grating thickness and period, as well as strictly control the divergence angle of incident beam. For the beam quality of writing laser beams, vibration and polarization will all have large effect on the grating's fringe homogeneity, it is necessary to optimize the writing process by adopting vibration-proof measures, optimizing writing light to uniform beam and tuning polarization directions parallel of both writing light beams to promote grating's diffraction efficiency and quality. The two-dimensional spatial imaging ability of VBG were validated. Under transmission incidence of wide spectral light source, the filtered bandpass was about 5 nm and spatial resolution was about 4 lines/mm; under diffuse reflection incidence, spatial resolution was about 4.9 lines/mm by adopting grating pair to compensate the dispersion.
-
Key words:
- diffraction optics /
- volume Bragg grating /
- coupled wave theory /
- spectral imaging
-
图 1 体布拉格光栅结构和波矢关系示意图
Figure 1. Structure scheme of volume Bragg grating (VBG) and vector relations in it
图 2 (a) 不同厚度周期比时的波长选择性曲线；(b)沿光栅厚度方向不同位置处各级次衍射光相对强度
Figure 2. (a)Wavelength selectivity curves of VBGs under different ratio of grating thickness and period; (b)diffraction efficiency of different diffraction orders along the direction of grating thickness
图 3 不同发散角时滤波谱宽比较
Figure 3. Filter spectral bandwidth under different divergence angles
图 4 实验光路示意图和PQ/PMMA聚合物透过率曲线
Figure 4. Experimental optical path distribution and transmission ratio of PQ/PMMA polymer
图 5 (a) 震动和(b)偏振一致性对衍射效率的影响
Figure 5. Effect of (a) vibration and (b) polarization on the diffraction efficiency
图 6 (a) 光束质量对衍射效率的影响；写入光束优化(b)前(c)后的体光栅的衍射光斑
Figure 6. (a) Effect of writing light beam quality on the diffraction efficiency, diffraction light facula with grating (b) before and (c) after the writing light beam quality optimization
图 8 (a) 透射式分辨率板成像结果；(b)滤波谱宽测量结果
Figure 8. (a) Imaging results of transmission resolution plate and (b) measurement of filtered bandpass
-
[1] Geissler P E, Greenberg R, Hoppa G, et al. Evolution of lineaments on Europa: Clues from Galileo multispectral imaging observa-tions[J]. Icarus, 1998, 135: 107-126. doi: 10.1006/icar.1998.5980 [2] Colarusso P, Kidder L H, Levein I W, et al. Infrared spectroscopic imaging: From planetary to cellular systems[J]. Applied Spectroscopy, 1998, 52: 106-120. doi: 10.1366/0003702981942401 [3] Levenson R M, Mansfield J R. Multispectral imaging in biology and medicine: Slices of life[J]. Cytom A, 2006, 69: 748-758. [4] Zhang L, Small G W. Automated detection of chemical vapors by pattern recognition analysis of passive multispectral infrared remote sensing imaging data[J]. Applied Spectroscopy, 2002, 56: 1082-1093. doi: 10.1366/000370202321274908 [5] Hiraoka Y, Shimi T, Haraguchi T. Multispectral imaging fluorescence microscopy for living cells[J]. Cell Structure and Function, 2002, 27: 367-374. doi: 10.1247/csf.27.367 [6] Shi T, DiMarzio C A. Multispectral method for skin imaging: development and validation[J]. Applied Optics, 2007, 46: 8619-8626. [7] Romier J, Selves J, Gastellu-Etchegorry J. Imaging spectrometer based on an acousto-optic tunable filter[J]. Rev Sci Instrum, 1998, 69: 2859-2867. doi: 10.1063/1.1149025 [8] Shingu H, Homma K, Kurosaki H, et al. Field observation of surface conditions using LCTF spectro-polarimeter[C]// Proc of SPIE. 2003, 5017: 116-127. [9] Blais-Ouellette S, Daigle O, Taylor K. The imaging Bragg tunable filter: a new path to integral field spectroscopy and narrow band imaging[C]//Proc of SPIE. 2006: 62695H. [10] Verhaegen M, Lessard S, Blais-Ouellette S. Narrow band SWIR hyperspectral imaging: a new approach based on volume Bragg grating[C]//Proc of SPIE. 2012: 83740G. [11] Kogelnik H. Coupled wave theory for thick hologram gratings[J]. Bell Syst Tech J, 1969, 48: 2909-2945. doi: 10.1002/j.1538-7305.1969.tb01198.x [12] 段佳著, 赵祥杰, 张大勇. 基于透射式体全息光栅的光学相控阵放大级研究[J]. 光学学报, 2014, 34: 0405002.Duan Jiazhu, Zhao Xiangjie, Zhang Dayong. Design of optical phased arrays amplifier stage based on volume holographic grating. Acta Optica Sinica, 2014, 34: 0405002 [13] Moharam M G, Gaylord T K. Rigorous coupled-wave analysis of planar-grating diffraction[J]. Journal of the Optical Society of America, 1981, 71(7): 811-818. doi: 10.1364/JOSA.71.000811 [14] Moharam M G, Gaylord T K, Magnusson R. Criteria for Bragg regime diffraction by phased gratings[J]. Optics Communication, 1980, 32(1): 14-18. 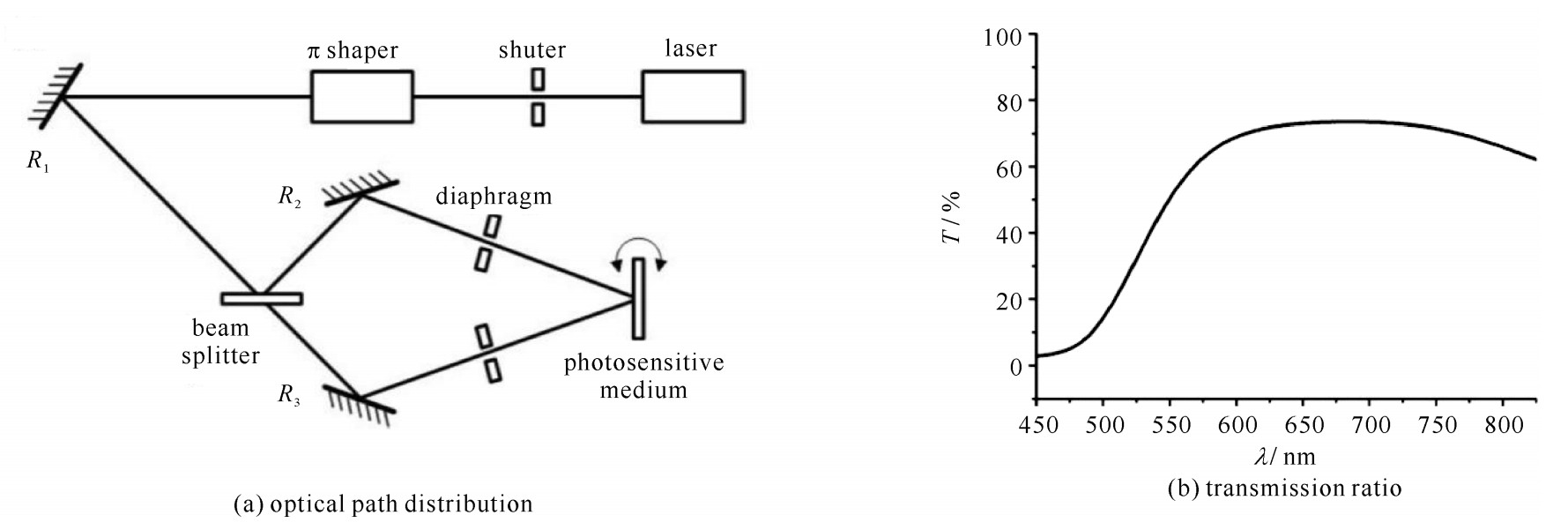[15] Laskin A, Laskin V. π Shaper-refractive beam shaping optics for advanced laser technologies[J]. Journal of Physics: Conference Series, 2011, 276: 012171. -
下载:
点击查看大图
计量
- 文章访问数: 1428
- HTML全文浏览量: 402
- PDF下载量: 206
- 被引次数: 0
