D-T中子源旋转靶活化计算与分析

高晖; 沈姚崧; 袁永刚

doi:10.11884/HPLPB201830.180039

D-T中子源旋转靶活化计算与分析

doi: 10.11884/HPLPB201830.180039

1.
中国工程物理研究院核物理与化学研究所, 四川绵阳 621999
2.
北京应用物理与计算数学研究所, 北京 100088

详细信息

作者简介:
高晖(1972—), 女，副研究员，主要从事辐射防护研究; qianliyan2005@caep.cn

中图分类号: TL64
计量
- 文章访问数: 879
- HTML全文浏览量: 258
- PDF下载量: 130
- 被引次数: 0
出版历程
- 收稿日期: 2018-01-26
- 修回日期: 2018-05-18
- 刊出日期: 2018-09-15

Activation calculation and analysis for rotary target chamber irradiated by D-T neutron

1.
Institute of Nuclear Physics and Chemistry, CAEP, Mianyang 621999, China
2.
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

摘要

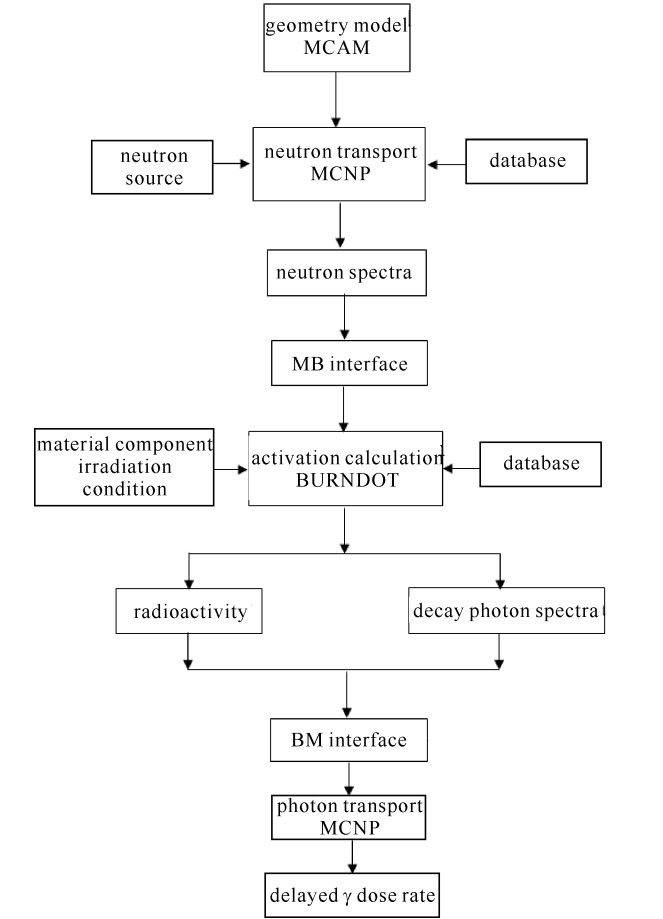
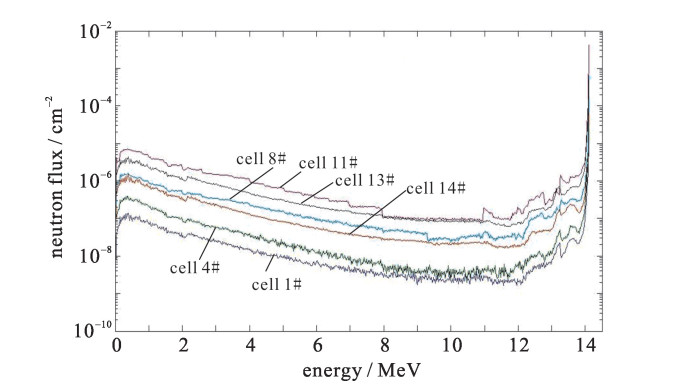
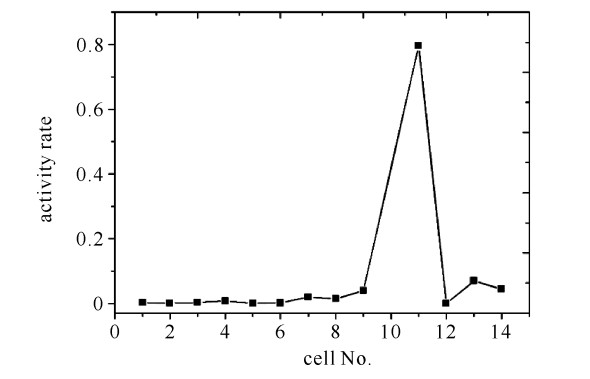
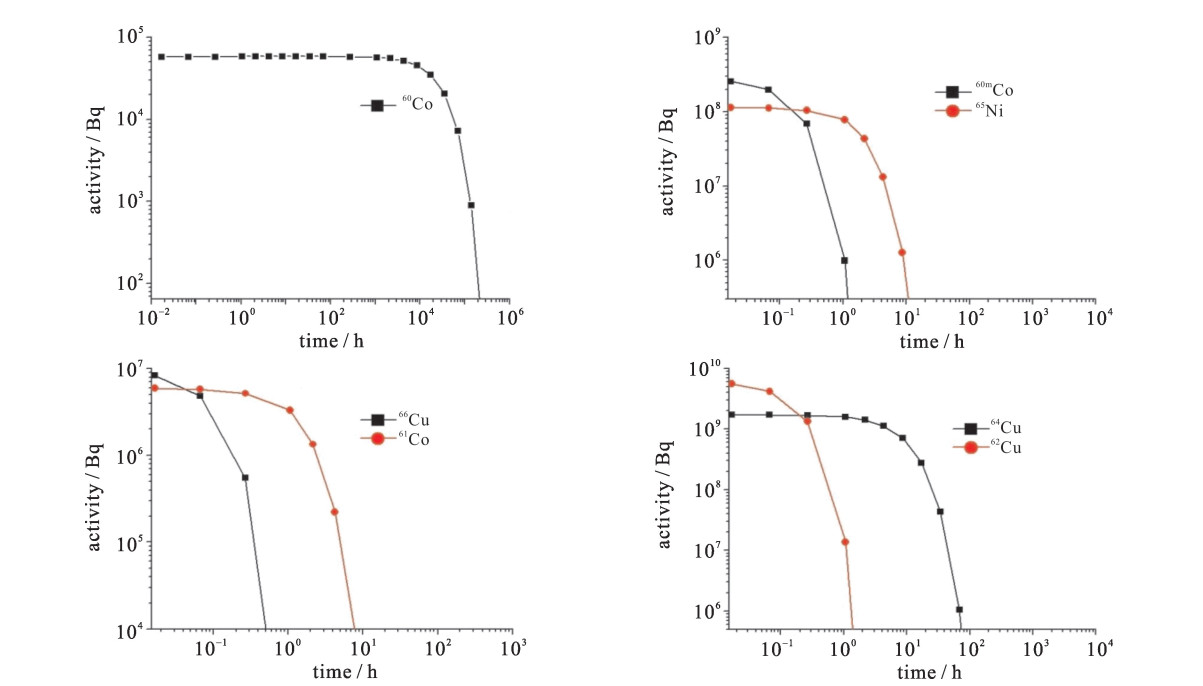
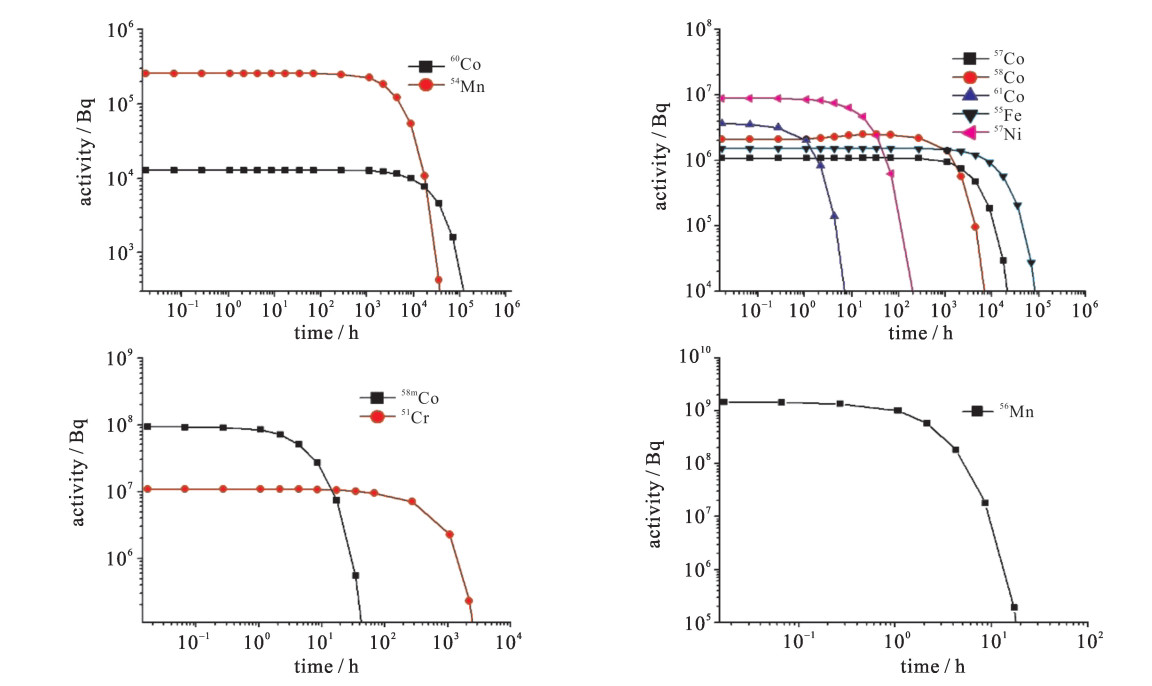
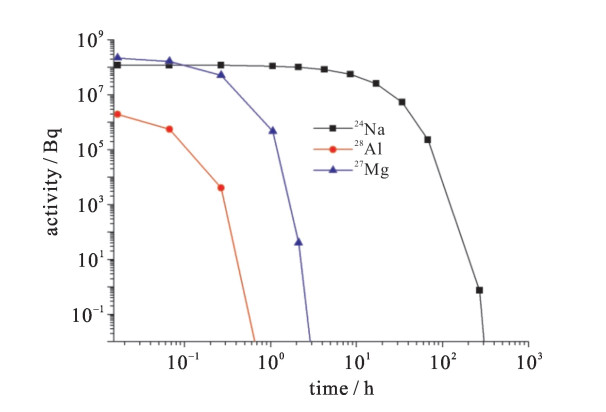
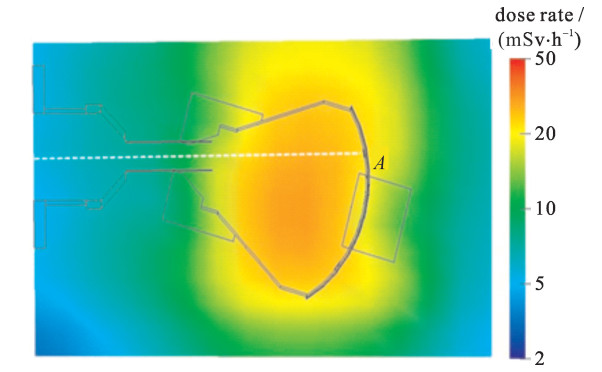
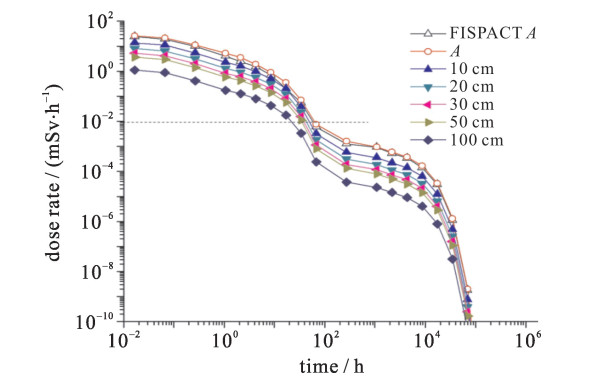
摘要: 为实现14 MeV D-T中子源旋转靶活化特性计算与分析，首次采用一种新的技术途径，将自主研发的活化程序BURNDOT与蒙特卡罗自动建模系统MCAM、蒙特卡罗粒子输运程序MCNP相结合，通过中子输运、材料活化、光子输运模拟计算的耦合，考察了材质、栅元、主要活化核素对靶室活化特性的影响。结果表明，约以辐照后68 h为界，材料铜、316不锈钢先后作为旋转靶室活度的主要贡献者，前者其产生的缓发γ剂量因⁶²Cu, ⁶⁴Cu核素的存在而达到活化剂量最大值，后者因有长半衰期核素⁵⁵Fe, ⁵⁷Co, ⁵⁴Mn等的存在，但其产生的剂量率值低于安全限值10 μSv/h。采用新方法的计算结果与采用欧洲活化程序FISPACT-2007的计算结果符合较好。
- BURNDOT /
- 旋转靶室 /
- 放射性活度 /
- 放射性核素 /
- 剂量率
Abstract: To realize the calculation and analysis for the neutron activation character of the 14 MeV D-T rotary target chamber, a new approach coupling the self-developed activation code BURNDOT with the Monte Carlo particle transport calculation code MCNP and the MCNP Automatic Modeling (MCAM) was developed, which integrates the functions of neutron transport, activation of materials and decay gamma transport.The influence of the factors including materials, cells and main activated nuclides on activation character of rotary target chamber at different time after the irradiation was analyzed in detail.The results show that the time about 68 hafter neutron radiation acts as a boundary, before it the copper material is the major contributor for activity instead of the 316 stainless steel after it.For the former, the delayedγdose rate up to maximum is due to 62 Cu and 64 Cu, and for the latter, the delayedγdose rate is influenced by the long life-time nuclides such as 55 Fe, 57 Co and 54 Mn and it is under the level of 10μSv/h.In addition, the results were compared with the data of the European activation code FISPACT-2007.
- BURNDOT /
- rotary target chamber /
- radioactivity /
- radioactive nuclide /
- dose rate

HTML全文

图 1 旋转靶室几何模型剖视图

Figure 1. Sectional view of geometrical modeling of rotary target chamber

下载: 全尺寸图片幻灯片

图 2 活化计算流程图

Figure 2. Flowchart of activation calculation

下载: 全尺寸图片幻灯片

图 3 中子能谱

Figure 3. Neutron spectra of cells

下载: 全尺寸图片幻灯片

图 4 不同栅元中子注量分布

Figure 4. Distribution of neutron flux of cells

下载: 全尺寸图片幻灯片

图 5 不同材料活度随时间变化曲线

Figure 5. Curves of activity generated from different materials vs time

下载: 全尺寸图片幻灯片

图 6 停止辐照初时(T=0)不同栅元活度贡献

Figure 6. Proportion of activity of cells at the first time after neutron radiation

下载: 全尺寸图片幻灯片

图 7 铜生核素的活度随时间变化曲线

Figure 7. Curves of nuclide activity generated from copper vs time

下载: 全尺寸图片幻灯片

图 8 316不锈钢生核素的活度随时间变化曲线

Figure 8. Curves of nuclide activity generated from 316 stainless steel vs time

下载: 全尺寸图片幻灯片

图 9 铝生核素的活度随时间变化曲线

Figure 9. Curves of nuclide activity generated from aluminum vs time

下载: 全尺寸图片幻灯片

图 10 停止辐照初时(t=0))缓发γ三维剂量场分布

Figure 10. Three dimensional delayed γ dose distribution right after neutron radiation

下载: 全尺寸图片幻灯片

图 11 辐照后缓发γ剂量率随距离变化曲线

Figure 11. Curves of delayed γ dose rate at different distance from point A after neutron radiation over 8 h

下载: 全尺寸图片幻灯片

图 12 A处缓发γ剂量率随栅元变化曲线

Figure 12. Curves of delayed γ dose rate from different cells at A location after neutron radiation

下载: 全尺寸图片幻灯片

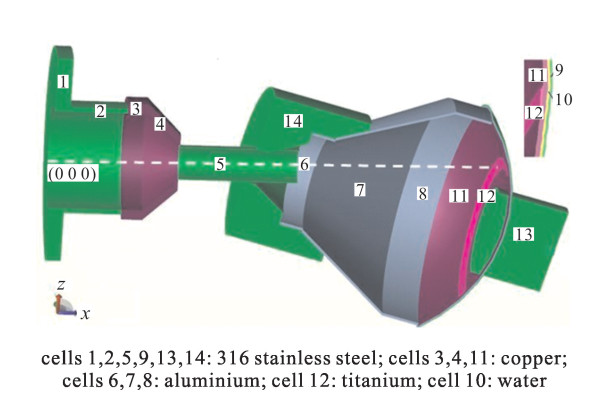
表 1 旋转靶室栅元结构参数

Table 1. Structure parameters of cells consisting the rotary target chamber

cell No.	material	volume/cm³	mass/g	function
1	316 stainless steel	401.730	3 166.20	activation
2	316 stainless steel	90.714	714.94	activation
3	pure copper	69.115	619.27	activation
4	pure copper	90.085	807.16	activation
5	316 stainless steel	11.819	93.15	activation
6	pure aluminum	18.148	49.00	activation
7	pure aluminum	147.800	399.06	activation
8	pure aluminum	64.280	173.56	activation
9	316 stainless steel	48.119	379.24	activation
10	water	16.840	16.84	cooling
11	pure copper	89.892	805.43	activation
12	pure titanium	0.204	0.92	activation
13	316 stainless steel	382.910	3 017.80	activation
14	316 stainless steel	1 146.400	9 035.20	activation

下载: 导出CSV

参考文献(10)

[1]	李德平, 潘自强. 辐射防护手册[M]. 北京: 原子能出版社, 1987. Li Deping, Pan Ziqiang. Radiation protection manual. Beijing: Atomic Energy Press, 1987
[2]	Shypailo R J. Stability evaluation and correction of a pulsed neutron generator prompt gamma activation analysis system[J]. J Radioanal Nucl Chem, 2016, 307: 1781-1786. doi: 10.1007/s10967-015-4440-7
[3]	Vuolo M, Bonifetto R, Dulla S, et al. Evaluation of the neutron activation of JET in-vessel components following DT irradiation[J]. Fusion Engineering and Design, 2014, 89: 2071-2075. doi: 10.1016/j.fusengdes.2014.02.050
[4]	Forrest R A. FISPACT-2007: User manual[R]. UKAEA FUS 534, 2007.
[5]	Croff A G. User's manual for Origen2 computer code[R]. ORNL/TM-7175, 1980.
[6]	Liu Xiaoping, Luo Yuetong, Tong Lili, et al. Development and application of MCNP auto-modeling tool: Mcam 3.0[J]. Fusion Engineering and Design, 2005, 75/79: 1275-1279. doi: 10.1016/j.fusengdes.2005.06.236
[7]	Briesmeister J F. MCNP―A general Monte Carlo N-particle transport code[R]. LA-370-M, 2000.
[8]	Rodenas J. Application of the Monte Carlo method to estimate doses due to neutron activation of different materials in a nuclear reactor[J]. Radiation Physics and Chemistry, 2017, 140: 442-446. doi: 10.1016/j.radphyschem.2017.02.015
[9]	Rodenas J, Gallardo S, Weirich F, et al. Application of dosimetry measurements to analyze the neutron activation of a stainless steel sample in a training nuclear reactor[J]. Radiat Phys Chem, 2014, 104: 368-371. doi: 10.1016/j.radphyschem.2014.05.013
[10]	Rodenas J, Abarca A, Gallardo S. Analysis of dose rates received around the storage pool for irradiated control rods in a BWR nuclear power plant[J]. Applied Radiation and Isotopes, 2011, 69: 1104-1107. doi: 10.1016/j.apradiso.2010.10.019