谐振腔侧边1×5介质柱调谐光子晶体滤波器

吴立恒; 王明红

doi:10.11884/HPLPB201931.180227

谐振腔侧边1×5介质柱调谐光子晶体滤波器

doi: 10.11884/HPLPB201931.180227

吴立恒,
王明红^,

聊城大学物理科学与信息工程学院, 山东聊城 252059

基金项目:

国家自然科学基金项目 11375081

详细信息

作者简介:
吴立恒(1980-)，男，硕士研究生，主要从事电磁场理论与技术、物理教学理论研究；wulihenglctu@163.com

通讯作者:
王明红(1967-)，男，教授，主要从事高功率微波与器件研究；wangminghong@lcu.edu.cn

中图分类号: TN248.1
计量
- 文章访问数: 1118
- HTML全文浏览量: 269
- PDF下载量: 81
- 被引次数: 0
出版历程
- 收稿日期: 2018-08-06
- 修回日期: 2018-12-10
- 刊出日期: 2019-01-15

Photonic crystal filter with 1×5 dielectric rod tuning beside a resonant cavity

Wu Liheng,
Wang Minghong^,

School of Physics Science & Information Engineering, Liaocheng University, Liaocheng 252059, China

摘要

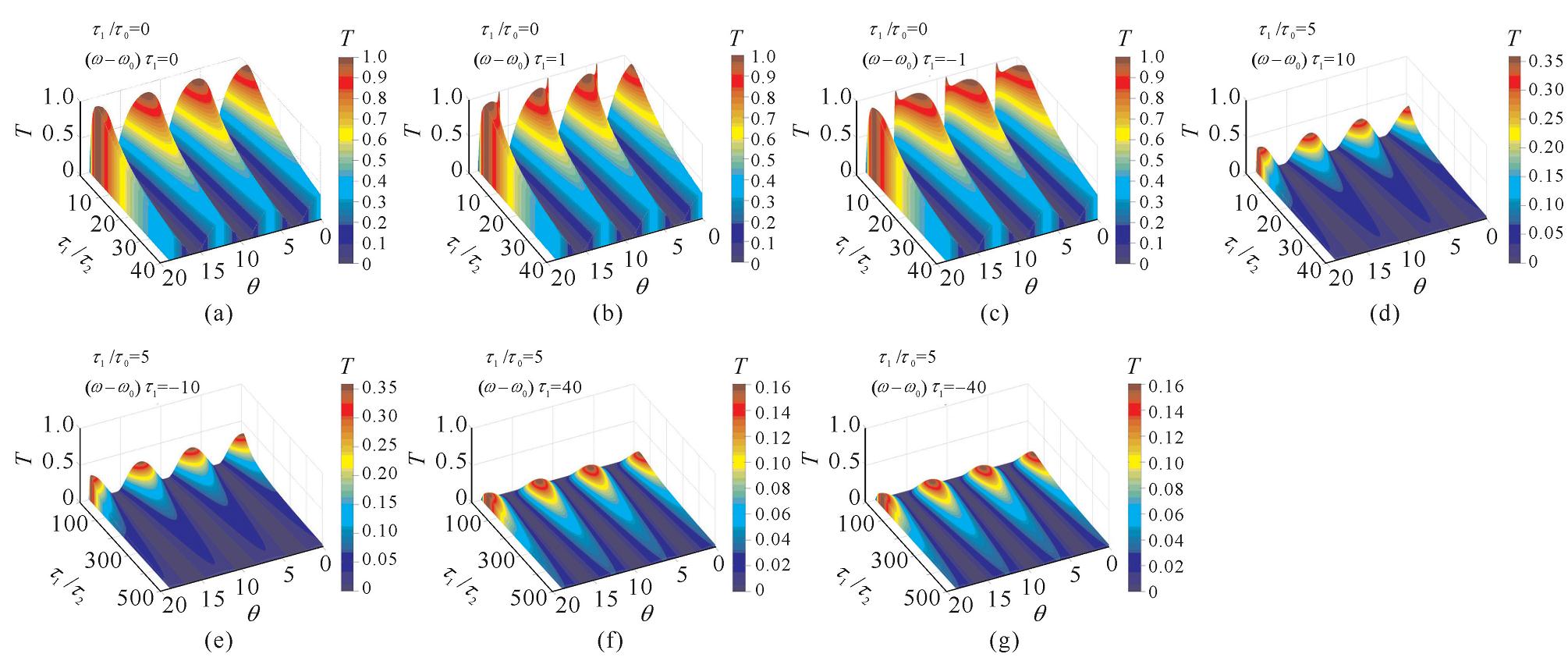
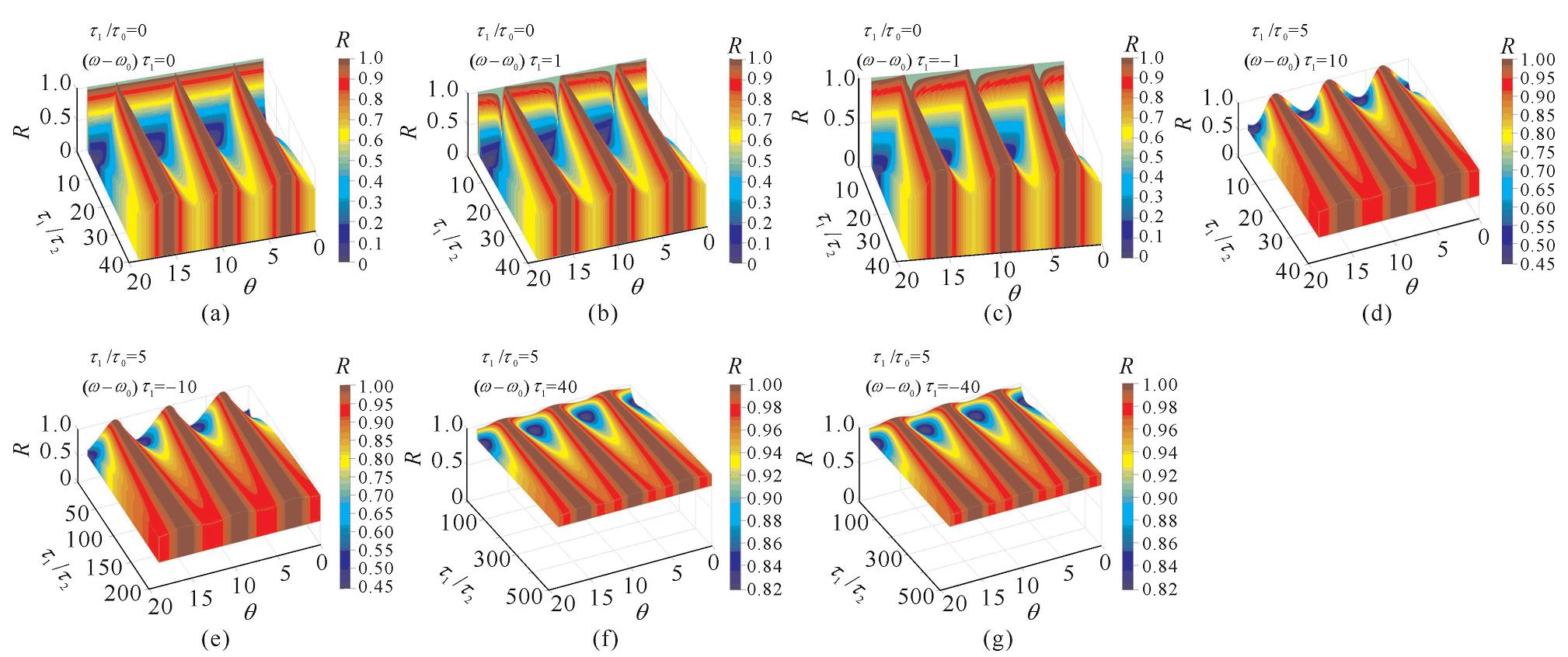
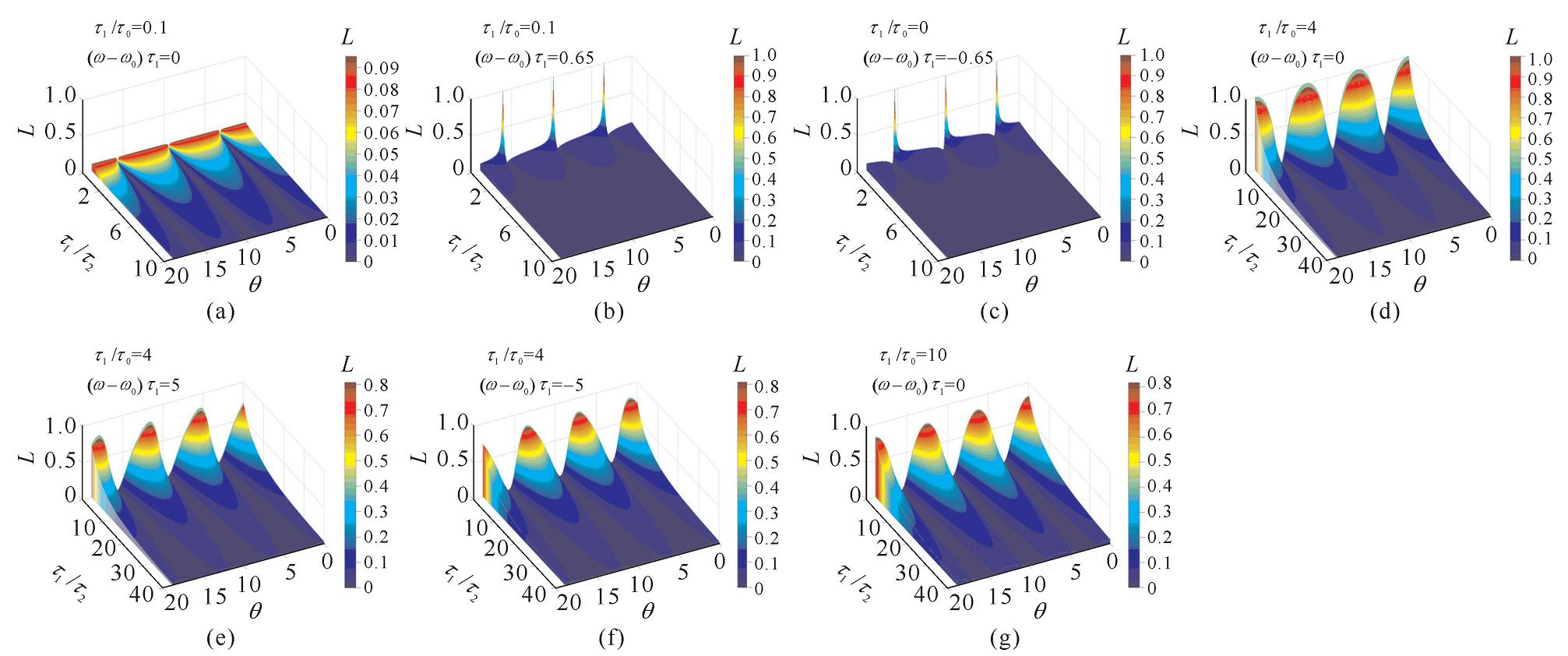
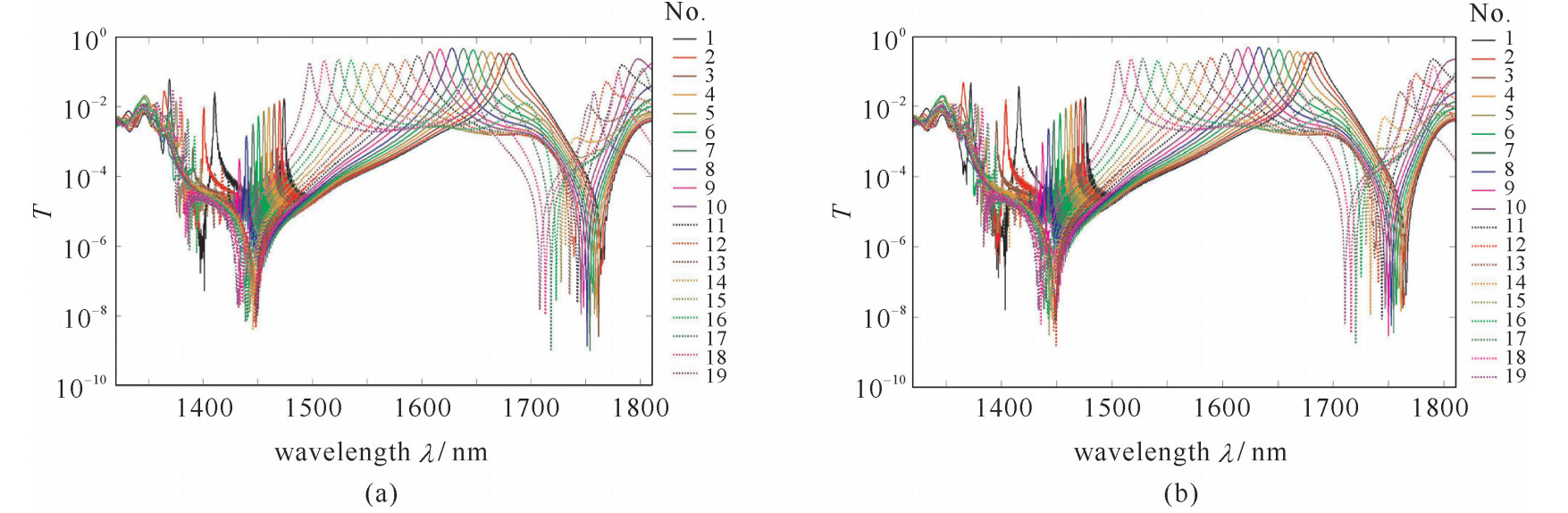
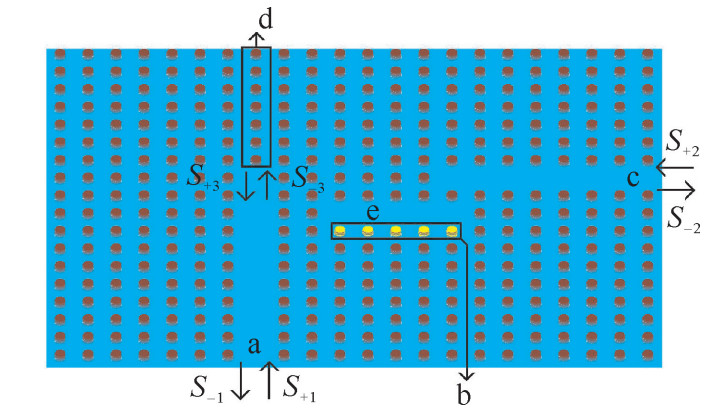
摘要: 在正方格二维光子晶体结构中设计了基于可调谐谐振腔的带通滤波器，通过改变1×5谐振腔侧边调谐介质柱位置调节谐振腔与波导系统工作时传输的波段，用CMT理论分析了输入端耦合衰减率及输入端失谐因子对滤波器的影响。借助FDTD方法得到了滤波器波长传输谱，结果表明：当滤波器结构工作于1320~1810 nm波长段时，输出端38个通帯的-3 dB带宽Δλ范围为4.18~11.15 nm，通带峰值波长可调宽度为186.56 nm。该微型滤波器适于光电通信粗波分解复用WDDM系统设计和光集成设计等方面。
- 介质柱调谐 /
- 波分解复用 /
- 输入端失谐因子 /
- 时域有限差分 /
- 耦合模理论 /
- 光子晶体滤波器
Abstract: Pass-band filter based on a tunable cavity is designed in 2-dimentional square-lattice photonic crystal structure. Operational transmission bands of the waveguide and cavity system are adjusted by changing positions of tuning dielectric rods beside the 1×5 resonant cavity. The effects of input port coupling decay ratio and input port detuning factors on the filter are analyzed by using CMT(Coupled-Mode Theory). Wavelength transmission spectra of the filter are calculated with the help of FDTD (finite difference time domain) method. The results show that -3 dB band width Δλ of output 38 pass-bands ranges from 4.18 nm to 11.15 nm when the filter operates over 1320-1810 nm wavelength band. Pass-band peak wavelength tuning width of the proposed structure is 186.56 nm. The micro filter is suitable for optical telecommunication course Wavelength Division Demultiplexing(WDDM) system design and optical integration design etc.
- dielectric rod tuning /
- Wavelength Division Demultiplexing(WDDM) /
- input port detuning factor /
- finite difference time domain(FDTD) /
- Coupled-Mode Theory(CMT) /
- photonic crystal filter

HTML全文

图 1 谐振腔侧边1×5介质柱调谐光子晶体滤波器

Figure 1. Photonic crystal filter with 1×5 dielectric rod tuning beside a resonant cavity

(a-Input port; b-Tuning rods below cavity c-Output port; d-Reflector; e-Cavity)

下载: 全尺寸图片幻灯片

图 2 调节参数τ₁/τ₀比值和输入端失谐因子(ω-ω₀)τ₁数值，输出信道正规化传输率T随θ和τ₁/τ₂比值的变化

Figure 2. Output channel normalized transmission T as a function of the ratio τ₁/τ₂ and θ at varying values of the ratio τ₁/τ₀ and input port detuning factor (ω-ω₀)τ₁

下载: 全尺寸图片幻灯片

图 3 调节参数τ₁/τ₀比值和输出端失谐谐因子(ω-ω₀)τ₁数值，输入端正规化反射率R随θ和τ₁/τ₂比值的变化

Figure 3. Input port normalized reflection R as a function of the ratio τ₁/τ₂ and θ at varying values of the ratio τ₁/τ₀ and input port detuning factor (ω-ω₀)τ₁

下载: 全尺寸图片幻灯片

图 4 调节参数τ₁/τ₀比值和输入端失谐谐因子(ω-ω₀)τ₁数值，谐振腔正规化损耗L随θ和τ₁/τ₂比值的变化

Figure 4. Cavity normalized loss L as a function of the ratio τ₁/τ₂ and θ at varying values of the ratio τ₁/τ₀ and input port detuning factor (ω-ω₀)τ₁

下载: 全尺寸图片幻灯片

图 5 改变谐振腔侧边1×5调谐柱位置得到光子晶体滤波器正规化功率传输谱

Figure 5. Normalized power transmission spectra of the photonic crystal filter with varying positions of 1×5 tuning dielectric rods beside the resonant cavity

下载: 全尺寸图片幻灯片

表 1 改变调谐介质柱位置时光子晶体滤波器具有的光学特性

Table 1. Optical properties of the photonic crystal filter with varying positions of the tuning dielectric rods

	No.	d/nm	λ/nm	T/dB	Δλ/nm		No.	d/nm	λ/nm	T/dB	Δλ/nm
Fig. 5(a)	1	266.8	1 684.01	-4.68	11.04	Fig. 5(b)	1	278.4	1 683.02	-4.71	11.15
	2	290.0	1 679.70	-4.74	10.85		2	301.6	1 678.16	-4.73	10.79
	3	313.2	1 674.67	-4.70	10.41		3	324.8	1 670.80	-4.64	9.71
	4	336.4	1 667.73	-4.55	9.69		4	348.0	1 663.13	-4.41	9.23
	5	359.6	1 660.08	-4.28	9.03		5	371.2	1 655.54	-4.08	8.70
	6	382.8	1 651.01	-3.86	8.45		6	394.4	1 646.88	-3.68	8.29
	7	406.0	1 641.65	-3.45	8.18		7	417.6	1 637.94	-3.33	8.14
	8	429.2	1 632.78	-3.21	8.18		8	440.8	1 627.64	-3.18	8.21
	9	452.4	1 622.90	-3.72	8.31		9	464.0	1 616.74	-3.53	8.53
	10	475.6	1 613.14	-3.78	9.77		10	487.2	1 607.42	-4.28	8.95
	11	498.8	1 601.73	-4.89	9.30		11	510.4	1 596.44	-5.50	9.65
	12	522.0	1 589.78	-6.25	10.14		12	533.6	1 584.92	-6.71	10.30
	13	545.2	1 578.70	-7.25	10.40		13	556.8	1 572.19	-7.62	10.41
	14	568.4	1 566.07	-7.79	10.07		14	580.0	1 558.66	-7.79	9.45
	15	591.6	1 553.98	-7.67	8.90		15	603.2	1 547.67	-7.41	8.10
	16	614.8	1 541.09	-7.08	7.32		16	626.4	1 535.21	-6.80	6.71
	17	638.0	1 528.05	-6.58	6.06		17	649.6	1 523.59	-6.47	5.64
	18	661.2	1 517.21	-6.52	5.02		18	672.8	1 510.88	-6.68	4.76
	19	684.4	1 505.23	-6.93	4.48		19	696.0	1 497.45	-7.38	4.18
Note: d represents the distance between rod center and the nearest dielectric cylinder

下载: 导出CSV

参考文献(19)

[1]	John S. Strong localization of photons in certain disordered dielectric superlattices[J]. Physical Review Letters, 1987, 58(23): 2486-2489. doi: 10.1103/PhysRevLett.58.2486
[2]	Mohammad A, Alireza T. Design and simulation of an optical channel drop filter based on two dimensional photonic crystal single ring race track resonator[J]. International Journal of Natural and Engineering Sciences, 2013, 7(1): 14-18.
[3]	Tavousi A, Mansouri-Birjandi M A, Saffari M, et al. Add-drop and channel-drop optical filters based on photonic crystal ring resonators[J]. International Journal of Communications and Information Technology, 2012, 1(2): 19-24.
[4]	Alipour-Banaei H, Mehdizadeh F, Hassangholizadeh-Kashtiban M, et al. A new proposal for PCRR-based channel drop filter using elliptical rings[J]. Physica E, 2014, 56(2): 211-215.
[5]	Qiao F, Zhang C, Wan J, et al. Photonic quantum-well structures multiple channeled filtering phenomena[J]. Applied Physics, 2000, 77(23): 3698-3700.
[6]	Alipour-Banaei H, Mehdizadeh F. Significant role of photonic crystal resonant cavities in WDM and DWDM communication tunable filters[J]. Optik, 2013, 124(17): 2639-2644. doi: 10.1016/j.ijleo.2012.07.029
[7]	Dideban A, Habibiyan H, Ghafoorifard H. Photonic crystal channel drop filter based on ring-shaped defects for DWDM systems[J]. Physica E: Low-dimensional Systems and Nanostructures, 2017, 87: 77-83. doi: 10.1016/j.physe.2016.11.022
[8]	Balaji V R, Murugan M, Robinson S. DWDM demultiplexer using inverted-p photonic crystal structure[J]. International Journal of Applied Engineering Research, 2015, 10(6): 0973-4562.
[9]	Hsueh W J, Wun S J, Lin Z J, et al. Features of the perfect transmission in Thue-Morse dielectric multilayers[J]. Journal of Optical Society of America B, 2011, 28(11): 2584-2591. doi: 10.1364/JOSAB.28.002584
[10]	Yusoff M H, Abu Hassan H, Hashim M R, et al. Hybrid photonic crystal 1.31/1.55 μm wavelength division multiplexer based on coupled line defect channels[J]. Optics Communication, 2011, 284(5): 1223-1227. doi: 10.1016/j.optcom.2010.11.018
[11]	Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Comput Phys, 1994, 114(2): 185-200. doi: 10.1006/jcph.1994.1159
[12]	Goldberg M. Stability criteria for finite difference approximations to parabolic systems[J]. Applied Numerical Mathematics, 2000, 33(1/4): 509-515.
[13]	Zhu Z, Brown T G. Full-vectorial finite-difference analysis of microstructured optical fibers[J]. Opt Express, 2002, 10(17): 853-864. doi: 10.1364/OE.10.000853
[14]	Ghaffari A, Monifi F, Djavid M, et al. Photonic crystal bends and power splitters based on ring resonators[J]. Optics Communications, 2008, 281(23): 5929-5934. doi: 10.1016/j.optcom.2008.09.015
[15]	Ghaffari A, Monifi F, Djavid M, et al. Analysis of photonic crystal power splitters with different configurations[J]. Journal of Applied Sciences, 2008, 8(8): 1416-1425. doi: 10.3923/jas.2008.1416.1425
[16]	Moloudian G, Sabbaghi-Nadooshan R, Hassangholizadeh-Kashtiban M. Design of all-optical tunable filter based on two-dimensional photonic crystals for WDM (wavedivision multiplexing) applications[J]. Journal of the Chinese Institute of Engineers, 2016, 39(8): 1-6.
[17]	Ahmad H, Reduan S A, Zulkifli A Z, et al. Tunable passively Q-switched thulium-fluoride fiber laser in the S+/S band (1450.0 to 1512.0 nm) region using a single-walled carbon-nanotube-based saturable absorber[J]. Applied Optics, 2017, 56(13): 3841-3847. doi: 10.1364/AO.56.003841
[18]	Gao F, Luo S, Ji H M, et al. Flat-topped ultrabroad stimulated emission from chirped InAs/InP quantum dot laser with spectral width of 92 nm[J]. Applied Physics Letters, 2016, 108(20): 883-795.
[19]	Xu H, Shi Y. Ultra-broadband 16-channel mode division (de)multiplexer utilizing densely packed bent waveguide arrays[J]. Optics Letters, 2016, 41(20): 4815-4818. doi: 10.1364/OL.41.004815