二维磁驱动数值模拟程序MDSC2的验证与确认

阚明先; 段书超; 张朝辉; 肖波; 王刚华; 王贵林; 冯春生; 彭洁

doi:10.11884/HPLPB201931.180300

二维磁驱动数值模拟程序MDSC2的验证与确认

doi: 10.11884/HPLPB201931.180300

1.
中国工程物理研究院流体物理研究所, 四川绵阳 621999
2.
湘潭大学数学与计算科学学院, 湖南湘潭 411105

基金项目:

国家自然科学基金项目 11405167

国家自然科学基金项目 11571293

详细信息

作者简介:
阚明先(1971—)，男，副研究员，研究方向为磁流体力学数值模拟；kanmx@caep.cn

中图分类号: O361.3
计量
- 文章访问数: 1186
- HTML全文浏览量: 291
- PDF下载量: 118
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-01
- 修回日期: 2019-03-01
- 刊出日期: 2019-07-15

Verification and validation of two dimensional magnetically driven simulation code MDSC2

1.
Institute of Fluid Physics, CAEP, P. O. Box 919-105, Mianyang 621999, China
2.
School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, China

摘要

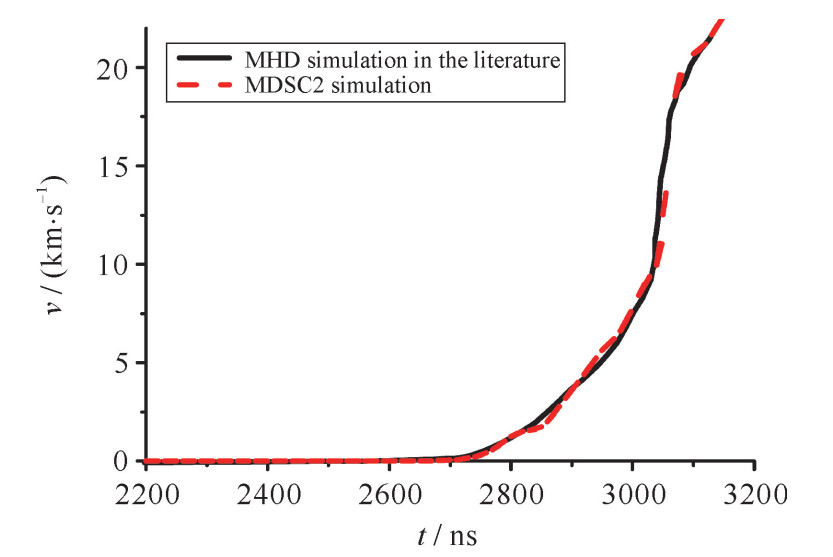
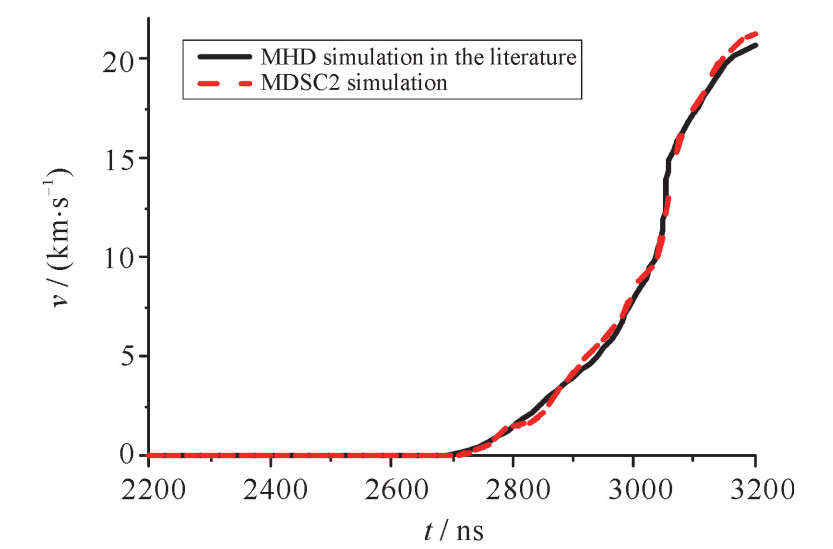
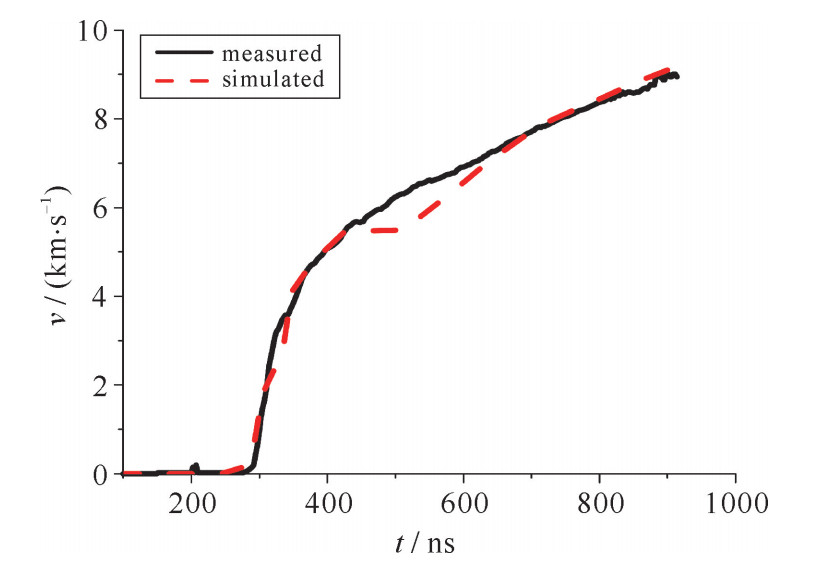
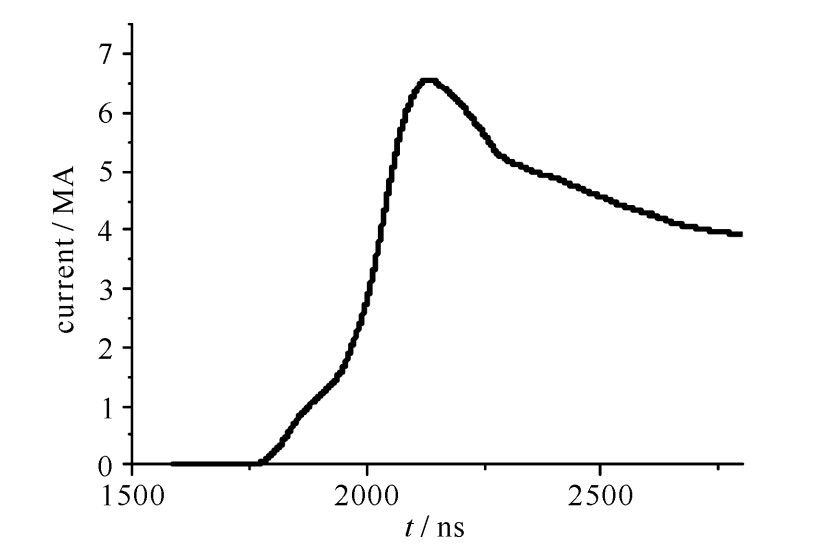
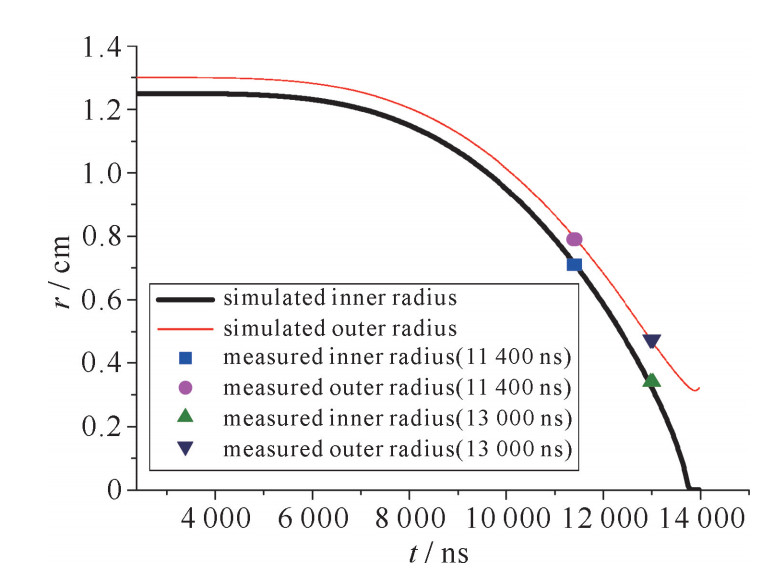
摘要: 为了对磁驱动实验提供高置信度的数值模拟，需要开展磁流体力学程序的验证与确认。采用人为解比较法、网格收敛性研究和与成熟程序比较等方法，对二维磁驱动数值模拟程序MDSC2进行了程序验证。数值模拟表明：MDSC2程序正确地表示了磁流体力学模型，其中热扩散、磁扩散的离散格式具有二阶收敛精度。采用与磁驱动实验相比较的方法，进行了MDSC2程序的确认。对聚龙一号装置上的PTS-061发次磁驱动单侧飞片发射和PTS-122发次磁驱动双侧飞片发射实验进行了模拟，模拟的飞片自由面速度与实验测量的飞片自由面速度相一致；对FP-1装置上的固体套筒实验进行了模拟，模拟的套筒内外半径与实验测量结果相一致。MDSC2程序能正确模拟磁驱动单侧飞片发射、磁驱动双侧飞片发射和磁驱动固体套筒等磁驱动实验。
- 二维磁驱动数值模拟程序 /
- 验证 /
- 确认 /
- 数值模拟
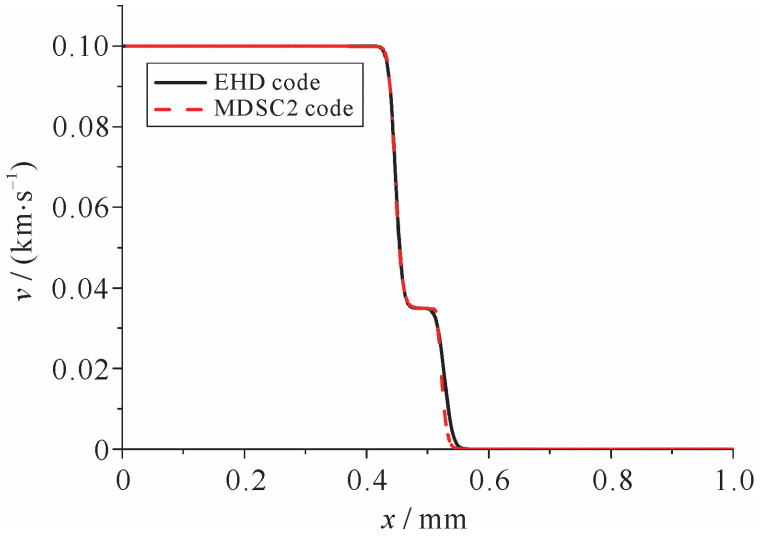
Abstract: Magneto-hydrodynamic (MHD) code has been widely used in the field of high current pulse technology, astrophysics and so on. Especially in recent years, with the rapid development of high pulse technology and magnetically driven experiments such as Z-pinch, magnetically driven flyer plate and magnetically driven quasi-isentropic/shock compression, experimental researchers and designers pay more and more attention to the correctness and reliability of MHD code. The verification and validation of the two dimensional magnetically driven simulation code MDSC2 is an important means to evaluate its correctness and reliability. In this paper, the MDSC2 code is verified by ways of comparison with artificial solutions, mesh convergence analysis and comparison with mature codes, and it is also validated by experiments, using magnetically driven one-sided flyer plate, magnetically driven two-sided flyer plates and magnetically driven solid liner. The numerical simulation shows that, the MDSC2 code not only correctly represents the MHD equations, but also can correctly simulate the magnetically driven experiments.
- two dimensional magnetically driven simulation code /
- verification /
- validation /
- numerical simulation

HTML全文

图 1 热扩散模型求解域Ω的示意图

Figure 1. Domain of thermal diffusion module

下载: 全尺寸图片幻灯片

图 2 求解域Ω在xy平面上的投影图

Figure 2. Cross section of 3D domain Ω on xy plane

下载: 全尺寸图片幻灯片

图 3 初始猜测磁场为驱动源模拟的飞片自由面速度

Figure 3. Simulated velocity histories (initially guessed B field as driving source)

下载: 全尺寸图片幻灯片

图 4 优化磁场为驱动源模拟的飞片自由面速度

Figure 4. Simulated velocity histories (optimized B field as driving source)

下载: 全尺寸图片幻灯片

图 5 EHD程序和MDSC2程序模拟的80 ns时的速度分布图

Figure 5. Velocity distribution of flyer plate(EHD vs MDSC2)

下载: 全尺寸图片幻灯片

图 6 PTS-061发次实验的电流加载历史

Figure 6. Measured current history of shot PTS-061

下载: 全尺寸图片幻灯片

图 7 模拟的PTS-061发次实验的速度历史

Figure 7. Simulated and measured velocity histories of shot PTS-061

下载: 全尺寸图片幻灯片

图 8 PTS-122发次实验的电流加载历史

Figure 8. Measured current history of shot PTS-122

下载: 全尺寸图片幻灯片

图 9 模拟的PTS-122发次实验的速度历史

Figure 9. Simulated and measured velocity histories of shot PTS-122

下载: 全尺寸图片幻灯片

图 10 磁驱动铝套筒实验测量电流

Figure 10. Measured current history on FP-1

下载: 全尺寸图片幻灯片

图 11 模拟的铝套筒平均内外半径历史

Figure 11. Histories of inner and outer radius of liner

下载: 全尺寸图片幻灯片

表 1 MDSC2程序中热扩散离散格式的逼近性

Table 1. Approximation of the discrete scheme of thermal diffusion equation in MDSC2 code

α/(°)	32×32 grid		64×64 grid		128×128 grid		256×256 grid
α/(°)	error	rate	error	rate	error	rate	error	rate
0	6.40×10^-4	-	1.60×10^-5	4.0	4.00×10^-6	4.0	1.00×10^-6	4.0
30	3.89×10^-4	-	9.94×10^-5	3.9	2.52×10^-5	3.9	6.35×10^-6	4.0
60	1.70×10^-3	-	4.45×10^-4	3.8	1.14×10^-4	3.9	2.87×10^-5	4.0
80	1.80×10^-2	-	4.71×10^-3	3.8	1.20×10^-3	3.8	3.04×10^-4	4.0

下载: 导出CSV

表 2 MDSC2程序中磁扩散方程离散格式的逼近性

Table 2. Approximation of the discrete scheme of magnetic diffusion equation in MDSC2 code

α/(°)	32×32 grid		64×64 grid		128×128 grid		256×256 grid
α/(°)	error	rate	error	rate	error	rate	error	rate
0	1.90×10^-4	-	4.74×10^-5	4.0	1.19×10^-5	4.0	2.97×10^-6	4.0
30	2.60×10^-4	-	6.61×10^-5	3.9	1.67×10^-5	4.0	4.20×10^-6	4.0
60	4.93×10^-4	-	1.29×10^-4	3.8	3.31×10^-5	3.9	8.39×10^-6	3.9
80	1.60×10^-3	-	4.36×10^-4	3.7	1.14×10^-4	3.8	2.94×10^-5	3.9

下载: 导出CSV

参考文献(25)

[1]	Matzen M K, Sweeney M A, Adams R G, et al. Pulsed-power-driven high energy density physics and inertial confinement fusion research[J]. Phys Plasmas, 2005, 12: 055503. doi: 10.1063/1.1891746
[2]	Peterson K J, Sinars D B, Yu E P, et al. Electrothermal instability growth in magnetically driven pulsed power liners[J]. Phys Plasmas, 2012, 19: 092701. doi: 10.1063/1.4751868
[3]	Knudson M D, Hanson D L, Bailey J E, et al. Equation of state measurements in liquid deuterium to 70 GPa[J]. Phys Rev Lett, 2001, 87: 225501. doi: 10.1103/PhysRevLett.87.225501
[4]	Lemke R W, Knudson M D, Davis J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator[J]. International Journal of Impact Engineering, 2011, 38(6): 480-485. doi: 10.1016/j.ijimpeng.2010.10.019
[5]	Davis J P, Brown J L, Knudson M D, et al. Analysis of shockless dynamic compression data on solids to multi-megabar pressures: Application to tantalum[J]. J Appl Phys, 2014, 116: 204903. doi: 10.1063/1.4902863
[6]	Frese M H. MACH2: A two-dimensional magneto-hydrodynamic simulation code for complex experimental configurations[R]. AMRC-R-874, 1987.
[7]	Robinson A C, Brunner T A, Carroll S, et al. ALEGRA: An arbitrary Lagrangian-Eulerian multimaterial, multiphysics code[C]//46th AIAA Areospace Sciences Meeting and Exhibit. 2008.
[8]	Chittenden J P, Lebedev S V, Jennings C A, et al. X-ray generation mechanisms in three-dimensional simulations of wire array Z-pinches[J]. Plasma Phys Control Fusion, 2004, 46: B457-B476. doi: 10.1088/0741-3335/46/12B/039
[9]	丁宁, 邬吉明, 杨震华, 等. Z箍缩内爆MRAED程序1维模拟分析[J], 强激光与粒子束, 2008, 20(2): 212-218. Ding Ning, Wu Jiming, Yang Zhenhua, et al. Simulation of Z-pinch implosion using MARED code. High Power Laser and Particle Beams, 20(2): 212-218
[10]	阚明先, 蒋吉昊, 王刚华, 等. 套筒内爆ALE方法二维MHD数值模拟[J]. 四川大学学报, 2007, 44(1): 91-96. https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX200701019.htm Kan Mingxian, Jiang Jihao, Wang Ganghua, et al. ALE simulation 2D MHD for liner. Journal of Sichuan University, 2007, 44(1): 91-96 https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX200701019.htm
[11]	阚明先, 王刚华, 赵海龙, 等. 磁驱动飞片二维磁流体力学数值模拟[J]. 强激光与粒子束, 2013, 25(8): 2137-2141. doi: 10.3788/HPLPB20132508.2137 Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Two dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates. High Power Laser and Particle Beams, 2013, 25(8): 2137-2141 doi: 10.3788/HPLPB20132508.2137
[12]	Ding Ning, Zhang Yang, Xiao Delong, et al. Theoretical and numerical research of wire array Z-pinch and dynamic hohlraum at IAPCM[J]. Matter and Radiation at Extremes, 2016, 1(3): 135-152. doi: 10.1016/j.mre.2016.06.001
[13]	阚明先, 王刚华, 肖波, 等. 二维弹塑性磁流体力学数值模拟[J], 强激光与粒子束, 2018, 30: 065002. doi: 10.11884/HPLPB201830.170306 Kan Mingxian, Wang Ganghua, Xiao Bo, et al. Two dimensional elasto-plastic MHD numerical simulation. High Power Laser and Particle Beams, 2018, 30: 065002 doi: 10.11884/HPLPB201830.170306
[14]	杨龙, 王刚华, 阚明先, 等. 基于MDSC程序的Z箍缩内爆单温和三温模拟分析[J]. 高压物理学报, 2016, 30(1): 64-70. Yang Long, Wang Ganghua, Kan Mingxian, et al. A numerical simulation analysis of mono-temperature and tri-temperature models by MDSC program in Z-pinch implosion. Chinese Journal of High Pressure Physics, 2016, 30(1): 64-70
[15]	Kan Mingxian, Zhang Zhaohui, Yang Long, et al. Simulation of magnetically driven flyer plate experiments with an improved magnetic field boundary formula[J]. High Energy Density Physics, 2018, 26: 38-43. doi: 10.1016/j.hedp.2017.12.002
[16]	阚明先, 张朝辉, 段书超, 等. "聚龙一号"装置上磁驱动铝飞片实验的数值模拟[J], 强激光与粒子束, 2015, 27: 125001. doi: 10.11884/HPLPB201527.125001 Kan Ming-xian, Zhang Zhaohui, Duan Shuchao, et al. Numerical simulation of magnetically driven aluminum flyer plate on PTS accelerator. High Power Laser and Particle Beams, 2015, 27: 125001 doi: 10.11884/HPLPB201527.125001
[17]	阚明先, 段书超, 王刚华, 等. 自由面被烧蚀飞片的数值模拟[J], 强激光与粒子束, 2017, 29: 045003. doi: 10.11884/HPLPB201729.160482 Kan Mingxian, Duan Shuchao, Wang Ganghua, et al. Numerical simulation of magnetically driven flyer plate of ablated free surface. High Power Laser and Particle Beams, 2017, 29: 045003 doi: 10.11884/HPLPB201729.160482
[18]	MacCormack R W. A perspective on a quarter century of CFD research[R]. AIAA -93-3291-CP, 1993.
[19]	杨明, 张冰, 马萍, 等. 仿真系统VV & A发展的五大关键问题[J]. 系统仿真学报, 2003, 15(11): 1506-1508. Yang Ming, Zhang Bing, Ma Ping, et al. Five key issues of the development of simulation systems VV & A. J Sys Simulation, 2003, 15(11): 1506-1508
[20]	王瑞利, 林忠, 袁国兴. 科学计算程序的验证与确认[J]. 北京理工大学学报, 2010, 30(3): 353-360. https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG201003023.htm Wang Ruili, Lin Zhong, Yuan Guoxing. Verification and validation in scientific computing code. Transactions of Beijing Institute of Technology, 2010, 30(3): 353-360 https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG201003023.htm
[21]	王瑞利, 温万治. 复杂工程和模拟的验证与确认[J]. 计算机辅助工程, 2014, 23(4): 61-68. https://www.cnki.com.cn/Article/CJFDTOTAL-JSFZ201404015.htm Wang Ruili, Wen Wanzhi. Verification and Validation of modeling and simulation of complex engineering. Computer Aided Engineering, 2014, 23(4): 61-68 https://www.cnki.com.cn/Article/CJFDTOTAL-JSFZ201404015.htm
[22]	阚明先, 王刚华, 赵海龙, 等. 金属电阻率模型. 爆炸与冲击, 2013, 33(3): 282-286. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201303009.htm Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Electrical resistivity model for metals. Explosion and Shock Waves, 2013, 33(3): 282-286 https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201303009.htm
[23]	Yao Songlin, Pei Xiaoyang, Yu Jidong, et al. A dislocation-based explanation of quasi-elastic release in shock-loaded aluminum[J]. J Appl Phys, 2017, 121: 035101.
[24]	Deng Jianjun, Xie Weiping, Feng Shuping, et al. Initial performance of the primary test stand[J]. IEEE Trans Plas Sci, 2013, 41(10): 2580-2583.
[25]	杨礼兵, 孙承纬, 廖海东, 等. 高能密度物理实验装置FP-1及其应用[J]. 强激光与粒子束, 2002, 14(5): 767-770. http://www.hplpb.com.cn/article/id/1404 Yang Libing, Sun Chengwei, Liao Haidong, et al. High energy density physics facility FP-1 and its applications. High Power Laser and Particle Beams, 2002, 14(5): 767-770 http://www.hplpb.com.cn/article/id/1404