Design of dual-band bandpass filter based on novel quad-mode resonator
-
摘要: 提出了一种新型的基于双枝节加载的T型四模谐振器，并且利用该谐振器设计了一款双模双通带带通滤波器。首先利用奇偶模分析法以及场分布分析法对四模谐振器的频率特性进行分析，谐振器的每一个谐振模式均可以被独立调节。然后对馈线枝节的参数进行了详细的分析，得到馈线对滤波器外部耦合系数的影响，以调整滤波器通带的带通宽度。接着分析滤波器传输零点产生的原因，得到零点变化的规律，从而调整零点位置，提高滤波器的选择性。缺陷地结构(DGS)被蚀刻在滤波器的金属层底面，以引入非谐振节点，提供源与负载的耦合，可以产生额外的传输零点，进一步提高滤波器的选择性，而且不会增大滤波器的体积。对该滤波器进行加工和测试，仿真结果与测试结果基本吻合。Abstract: In this paper, a novel dual-mode dual-band bandpass filter using a quad-mode dual-stub loaded T-type resonator is proposed. The quad-mode resonator is analyzed using odd-/even-mode method. Field distribution of each mode is illustrated, and each mode can be independently controlled. The required extra quality factor (Qe) can be realized by determining the proper feed-lines parameters, and detail analysis is provided to adjust bandwidth of filter passbands. Then the cause of the zero point of the filter transmission is analyzed get the rule of the zero point change is got for adjusting the zero position and improving the selectivity of the filter. defected ground structure (DGS), etched on the bottom metal surface of the filter, working as a non-resonant node (NRN) and proving source-to-load coupling, are utilized to introduce extra transmission zero to improve the passband selectivity without increasing filter volume. The filter was designed and fabricated, and the simulated results are in accordance with the measured results.
-
随着现代无线通信的快速发展，越来越多的通信系统工作在两个频段，例如全球无线通信系统(GSM)，全球定位系统(GPS)，4G通信以及5G通信等。滤波器作为射频/微波系统不可或缺的一部分，相较于对每个通信频段单独设计一个对应的滤波器，双通带滤波器即节省了成本又减小了通信系统的尺寸。目前，对双通带带通滤波器提出了更多的要求：高选择性，低损耗，高带外抑制，可集成化。已经有多种设计双通带带通滤波器的结构被提出，这些设计方法可以总结为以下几种：
(1) 利用适当的输入输出馈线将两个中心频率不同的带通滤波器并联设计为双通带带通滤波器。这种设计方式将不同工作频率的滤波器组合在一起，可以灵活地控制滤波器的中心频率以及带通宽度。例如，文献[1]中将两个四模谐振器共用一个输入输出馈线设计了WLAN和WIMAX频段的双通带带通滤波器，文献[2]将两个E型阶跃阻抗谐振器(SIR) 和开环谐振器设计了一款DBBPF，其中E型谐振器工作在较高的谐振频段，开口环谐振器工作在较低的工作频段。但是这种设计方式会使得滤波器的尺寸明显增大。为了减小滤波器的尺寸，一些学者使用嵌套环形谐振器设计双通带带通滤波器[3-4]，文献[3]中将一个圆环形枝节加载谐振器与另一个开口环形阶跃阻抗谐振器组合设计了一个双通带滤波器，但是该设计中的内圈谐振器需要通过外圈谐振器耦合激励，导致外部耦合系数(Qe)值无法调节；文献[4]中利用共面波导(CPW)对两个环形谐振器分别馈电；文献[5]中为了方便馈电采用多层结构，这两种方式都会增加设计的难度。
(2) 耦合两个双模谐振器构成双通带带通滤波器，这种设计方式被广泛的利用设计双通带带通滤波器。主要采用阶跃阻抗谐振器(SIR)[6-8]，枝节加载谐振器(SLR)[9-11]等。这种设计方式具有较好的设计灵活性，可以独立控制滤波器的中心频率和带宽，而且耦合系数以及Qe可以被调节。但是这种设计方式很难将多个谐振器耦合设计更高阶的滤波器。虽然利用基片基层波导(SIW)[12-14]谐振器的高阶特性也可以设计双通带通带带通滤波器，但是SIW的尺寸更大，而且灵活性较差。
(3) 将四模或者更高模谐振器的谐振模式分为高频和低频两组设计为双通带滤波器。因为四模谐振器的设计灵活性以及小型化特性，使用四模谐振器设计双模双通带带通滤波器是目前被广泛讨论的设计方法[15-17]。枝节加载谐振器[15]，环形谐振器[16]以及耦合线结构被广泛的用于四模谐振器的设计。在文献[15]中，通过引入加载枝节之间的耦合将三模谐振器的奇模谐振模式分为两个谐振模式，形成四模谐振器，所以它的奇模频率不能分别调节。在文献[16]中的四模谐振器通过环形谐振器加载5个开路枝节实现，然而该谐振器设计的双通带滤波器带宽不可调。文献[17]的四模谐振器由一对耦合线枝节和传输线枝节构成，但是该谐振器的结构过于复杂。
在本文中，使用四模谐振器设计了一种新的双通带带通滤波器。该四模谐振器由两个开路枝节加载到T型谐振上构成。采用奇偶模分析法计算谐振器的谐振频率以及采用场分布分析方法分析谐振器的谐振模式，每一个模式都可以被独立控制。为了更好地激励起四个谐振模式，使用双输入输出枝节耦合电路进行馈电。对滤波器的传输零点进行分析，调整零点的位置，提高滤波器的选择性。在滤波器的底端蚀刻DGS，引入非谐振节点，可以提供一个额外的传输零点，进一步提高滤波器的选择性。对该滤波器仿真，加工以及测试，测试结果与仿真结果基本吻合。
1. 谐振器分析
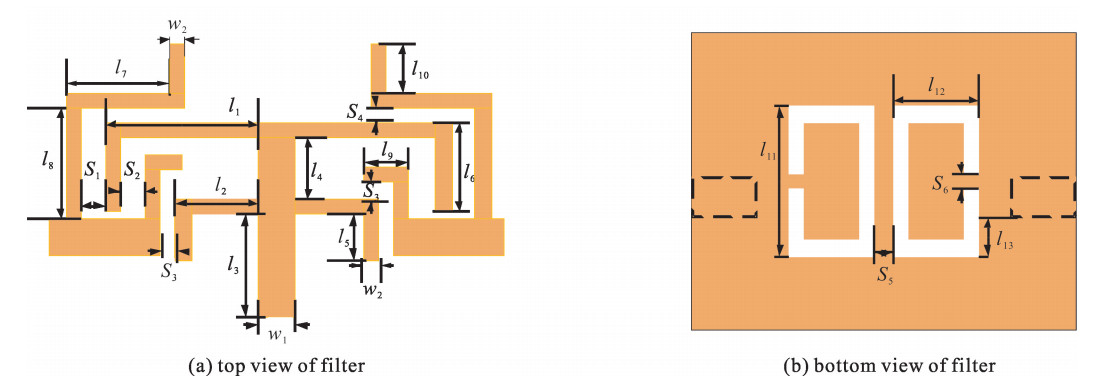
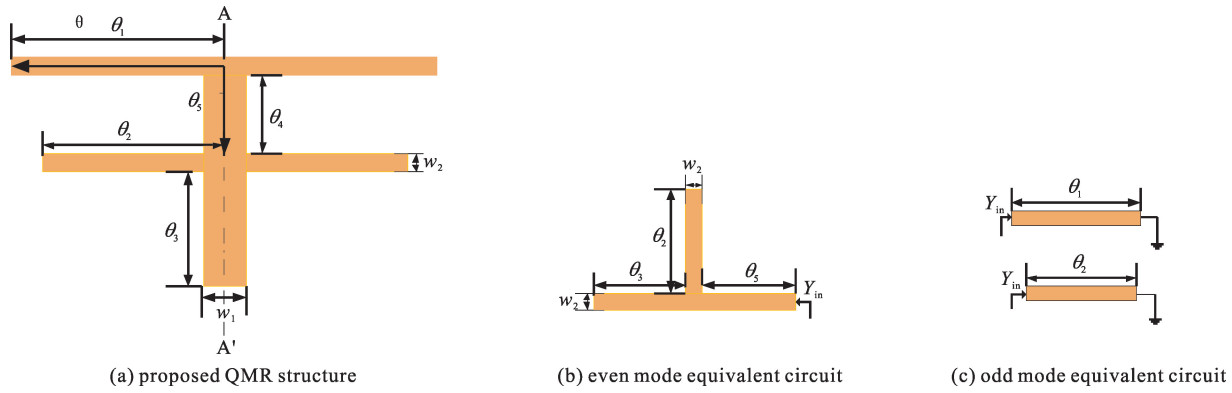
四模谐振器的结构如图 1(a)所示，为了方便分析与计算取w1=2w2。由于谐振器结构关于AA′对称，采用奇偶模分析法分析谐振器的谐振特性。谐振器的偶模等效电路为枝节加载谐振器，如图 1(b)所示，这是一种典型的双模谐振器。奇模谐振电路为两个短路枝节，如图 1(c)所示。
图 1 (a) 四模谐振器的结构, (b)偶模等效电路, (c)奇模等效电路Figure 1. Structure and equivalent circuits of quad-mode resonator (QMR)偶模等效电路的输入阻抗为
Yin,eve=jYtanθ2+tanθ3+tanθ51−tanθ5(tanθ2+tanθ3) (1) 式中：Y表示特性阻抗，θ5=θ1+θ4。
偶模等效电路的谐振条件可以表示为
tanθ2+tanθ3+tanθ5=0 (2) 由公式(2)得到偶模的两个谐振频率为feve1和feve2。奇模的等效电路如图 1(c)所示，两个短路枝节分别为两个1/4波长谐振器，它们的等效电路的谐振条件可以被直接得到
Yin, odd 1=jYtanθ1 (3) Yin, odd 2=jYtanθ2 (4) 从而可以计算得到枝节θ1的谐振频率为fodd1，枝节θ2的谐振频率为fodd2。
四个谐振模式的场分布如图 2所示。谐振模式feve1由枝节θ5与枝节θ3构成的1/2波长谐振器产生，如图 2(a)所示；同样，图 2(b)给出了谐振模式fodd1由枝节θ1构成的1/4波长谐振器产生；如图 2(c)所示，谐振模式feve2由枝节θ2和枝节θ3控制，这两个枝节构成了1/2波长谐振器；在图 2(d)中，枝节θ2构成1/4波长谐振器，它的谐振模式为fodd2。
图 2 (a) feve1的场分布; (b) fodd1的场分布; (c) feve2的场分布; (d) fodd2的场分布Figure 2. Field distribution of four resonating modes从场分布以及谐振器的谐振条件可以得到谐振频率随枝节改变的变化规律。当θ1增加时，fodd1和feve1将会减小；同样，θ2增加，fodd2和feve2也随之减小。当θ3改变，偶模激励的两个模式将会随之改变，feve1和feve2随着θ3的减小而增大，但是奇模频率不发生改变；同样的feve1与θ4成反比，而且θ4改变时不影响其他谐振频率。因此，四模谐振器的每一个谐振频率都可以被独立地控制和调节，具备设计为双通带带通滤波器的条件。
2. 滤波器设计
为了更好地控制滤波器的中心频率，fodd1和feve1被用来构成较低频率的通带，通带的中心频率可以由枝节θ1控制；fodd2和feve2被用来构成较高频率的通带，通带的中心频率可以由枝节θ2控制。滤波器的整体拓扑结构如图 3所示。谐振器产生的四个谐振模式因为正交性不会产生相互耦合，源与负载之间的耦合通过额外引入DGS实现非谐振节点，并且不会增加滤波器的体积。
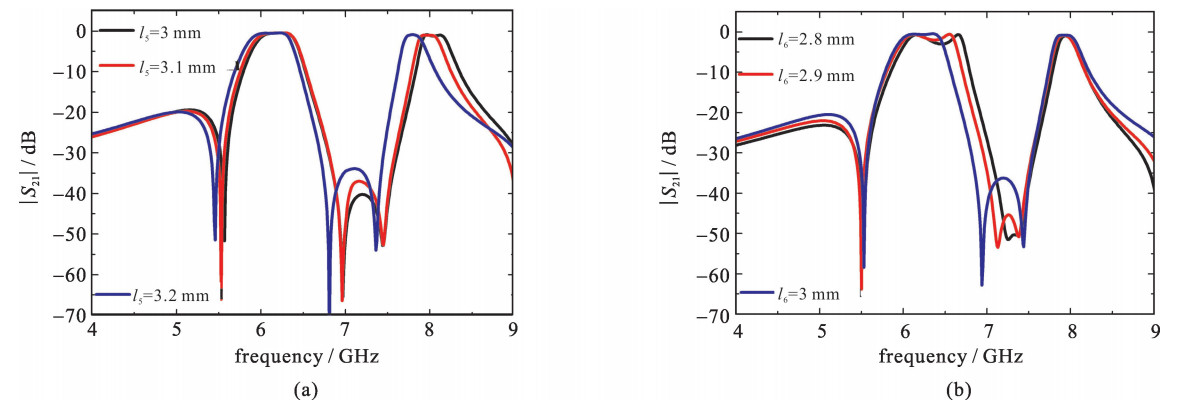
为了更好地激励起四个谐振模式，滤波器设计采用双枝节输入输出馈线，如图 4(a)所示。第一步，设计中心频率。结合上述分析以及图 4(a)可以得到，滤波器低频通带的两个谐振频率分别由l1+l6和l1+l6+l3+l4决定；同理，滤波器高频通带的两个谐振频率分别由l2+l5和l2+l5+l3决定。所以两个通带的中心频率可以被独立地控制，通过调节两个加载枝节的长度。图 5给出了双通带随的枝节l5和l6变化的响应曲线。从图 5(a)中可以得到随着l5的增大，高频通带的中心频率减小，低频通带基本保持不变。同样l6的增加导致低频通带的中心频率向更低频移动，高频通带保持不变。
当滤波器的中心频率被确定之后，下一步通过调整馈线的位置或者尺寸以调整滤波器的Qe，获得需要的带通宽度。
Qe=ω0/Δω3 dB (5) 式中: ω0为通带的中心频率；Δω3 dB为S21相对中心频率变化3 dB的带宽。通过仿真分析，S4和S3对滤波器的Qe影响较大。如图 6(a)所示，高频通带的Qe2与S4成正比，低频通带的Qe1也随着S4的增大而增大，也就意味着，当S4增大时，两个通带的带宽都会减小。Qe1和Qe2随S3的变化如图 6(b)所示，Qe2与S3成正比，但是Qe1并不随着S3的改变而变化，所以，S3只会影响高频通带的带宽，对低频通带的带宽没有影响。
该滤波器存在3个传输零点(TZ1, TZ2, TZ3)，零点位置的变化规律被分析出来，如图 7所示。
图 7 传输零点随参数的变化Figure 7. Variation of the transmission zeros (TZs) with varied parameters图 7(a)给出了TZ1随枝节l1+l6的变化。可以得到，当l1+l6=10.7 mm时，TZ1位于低频通带的右侧；当l1+l6=8.7 mm时，TZ1位于低频通带的左侧。当谐振器的尺寸改变时，滤波器的耦合矩阵发生了改变，从而零点的位置也随之变化。为了方便分析，可以将两个通带单独讨论，双模带通滤波器传输零点的位置计算公式为[18]
Ω=(M11M2s2−M22M2s1)(M2s1−M2s2) (6) 由式(6)可以得到，当Ms12 < Ms22且M11 < 0, M22>0时，传输零点位于通带的上阻带。给出零点位于低频通带左侧的耦合矩阵，如表 1所示。低频通带的耦合矩阵符合M11 < 0, M22>0的结果。
表 1 低频通带的耦合矩阵Table 1. Coupling matrix of low frequency passbandM S 1 2 L S 0 0.022 0.026 0 1 0.022 0.047 0 -0.022 2 0.026 0 -0.045 0.026 L 0 -0.022 0.026 0 当S4增加时，TZ2向低频移动，而其他两个零点并不发生变化，如图 7(b)。两个馈电枝节分别耦合到加载枝节l1+l6和l2+l5形成了两条传输路径。由输入到输出端口，这两条传输路径的相位在TZ2的位置相反，形成传输零点。所以TZ2位于两个通带之间，而且可以通过调节馈线调节TZ2的位置。
图 7(c)给出了TZ3随枝节l3的变化。当l3=6.8 mm时，TZ3位于高频通带的右侧，而当l3=6.5 mm时，传输零点TZ3位于高频通带的左侧。可以得到TZ3与TZ1具有相同的性质。这两个传输零点均是因为构成的枝节加载谐振器在谐振器的尺寸改变时，耦合矩阵发生了改变，零点的位置也随之改变，改变规律同样为公式(6)。给出零点位于高频通带左侧时的耦合矩阵，如表 2所示。由表 2可知，高频通带的耦合矩阵同样符合M11 < 0, M22>0的结果。
表 2 高频通带的耦合矩阵Table 2. Coupling matrix of high frequency passbandM S 3 4 L S 0 0.019 0.036 0 3 0.019 0.051 0 -0.019 4 0.036 0 -0.045 0.036 L 0 -0.019 0.036 0 为了滤波器具有更好的选择性，调节TZ1使它位于低频通带的左侧，然后调整馈线使得TZ2靠近低频通带，再调整TZ3的位置，使它位于高频通带的左侧。结果如图 8中的虚线所示，此时滤波器的上阻带以及带间隔离度都有着良好的抑制。
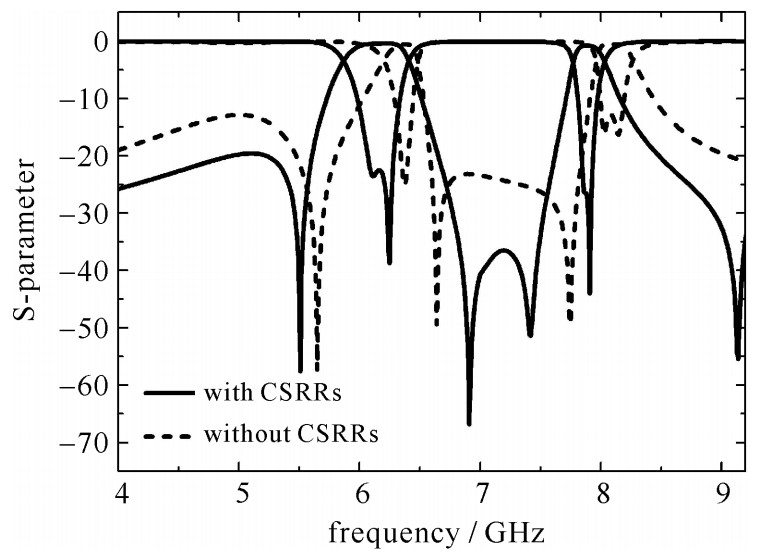
图 8 蚀刻DGS与不蚀刻DGS的对比Figure 8. Comparison of filter response with defected ground structure (DGS) and without DGS但是在下阻带，滤波器的带外抑制做的并不好，选择性较差。为了进一步提高滤波器的选择性，同时不增大滤波器的体积，在滤波器的底端蚀刻DGS，如图 4(b)所示。这样可以在带外引入一个非谐振节点，额外提供一个传输零点。图 8给出了蚀刻DGS与不蚀刻DGS的区别，可以得到在滤波器的下阻带的选择性有了极大的提高，而且滤波器的带间隔离度也有着较大的改善，同时上阻带的抑制也得到了提高。
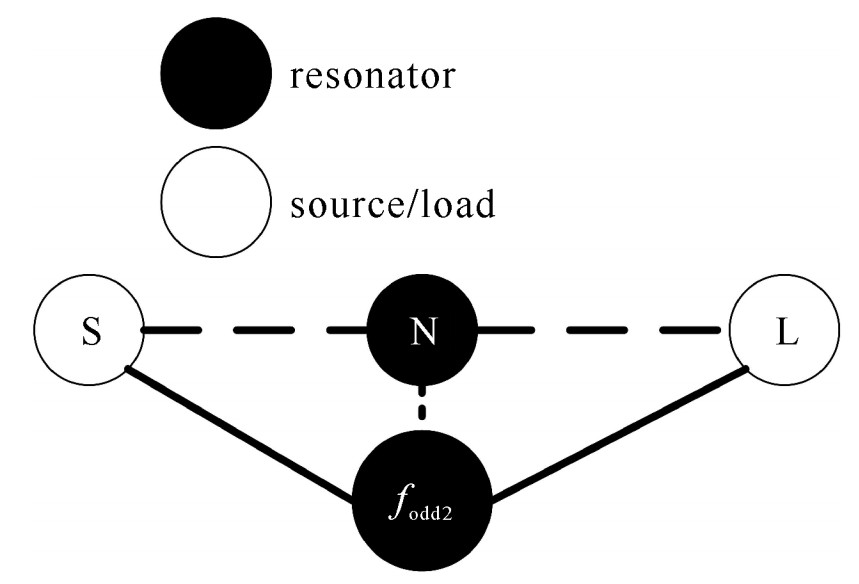
将DGS看做NRN，分别与源、负载以及fodd2模式发生耦合，从而通过耦合系数的分析来确定零点的位置。因为其他谐振模式之间不存在耦合，所以可以将与DGS发生耦合的部分单独提取出来进行分析，如图 9所示。
此时可以计算得到传输零点的表达式为
Ω=−−M33MLNMSN+M3 N(ML3MSN+MLNMS3)−MNNML3MS3ML3MS3+MLNMSN (7) 公式(7)中下标N表示NRN，3表示fodd2。在文献[18]以及之前的分析中可以知道ML3=－MS3，代入到公式(7)中得到
Ω=−−M33MLNMSN+M3 NMS3(MSN−MLN)+MNNM2S3−M2S3+MLNMSN (8) 由公式(8)可知，当MLN=MSN时，零点位置的变化规律与公式(6)相同，此时调节NRN的谐振频率，将DGS的谐振频率由远大于fodd2，逐步调整为DGS的谐振频率小于fodd2，零点的位置将会由fTZ>fNRN>fodd2移动到fTZ < fNRN < fodd2，刚好满足DGS开口相向时的频率变化规律。当MLN=－MSN时，为了简化分析，仅对本文中的情况进行分析。令|MNN|≫|M33|，因为NRN位于通带的上方，所以MNN < 0。而且，源或者负载对于fodd2的耦合明显强于对NRN的耦合，所以|MS3|>|MSN|，代入公式(8)可以得到MNN < Ω < 0，此时传输零点位于fodd2与NRN的中间，刚好满足DGS开口相背时的频率变化。
接下来只要验证两种情况之下MSN与MLN的关系即可以得到蚀刻DGS的零点变化规律。由电磁仿真软件分析底面蚀刻DGS的场分布可以得到，当开口相向时，谐振器的电场是同相的；当开口相背时，谐振器的电场为反向的，所以可以得到结论：当DGS开口相背时，MLN=－MSN；当DGS开口相向时MLN=MSN。
表 3 NRN的耦合矩阵Table 3. Coupling matrix of non-resonant node (NRN)M S 3 N L S 0 0.895 2 1.112 4 0 3 0.895 2 0.187 3 1.211 5 -0.895 2 N 1.112 4 1.211 5 -19.772 -1.112 4 L 0 -0.895 2 -1.112 4 0 根据上述分析采用开口相背的方式蚀刻DGS，从而提高滤波器高频通带的选择性，而且NRN位于远离通带的位置。同样也可以换个设计思路，当采用开口相向的方式设计传输零点，可以将DGS的谐振频率调节至靠近高频通带的位置，在通带上方引入一个传输零点，以提高选择性，而且可以将滤波器高频通带的阶数提高至3阶。但是因为时间原因本文不再设计相关结构。
3. 测试
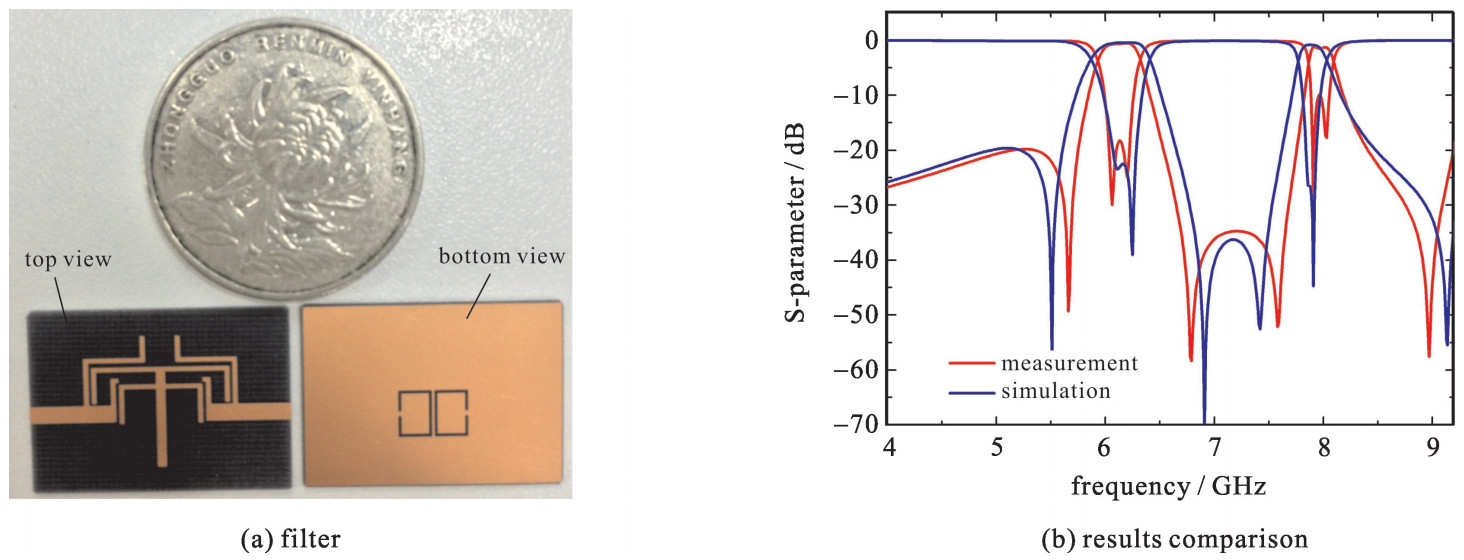
本文中，采用F4b的介质材料，相对介电常数为2.2，基板厚度为0.5 mm。经过仿真可以得到最后滤波器的尺寸为：l1=5.9 mm, l2=3.4 mm, l3=7.2 mm, l4=1.2 mm, l5=3.2 mm, l6=2.9 mm, l7=5.2 mm, l8=4.35 mm, l9=0.7 mm, l10=2 mm, l11=4.3 mm, l12=3.1 mm, l13=0.95 mm, w1=0.8 mm, w2=0.4 mm, S1=0.3 mm, S2=1.35 mm, S3=0.35 mm, S4=0.45 mm, S5=0.2 mm, S6=0.4 mm。整个电路的尺寸为0.43λg×0.38λg，其中λg是低频通带的中心频率的波导波长。图 10(a)给出了滤波器的加工实物，图 10(b)给出了仿真结果与测试结果的对比。仿真与测试结果基本吻合，两个通带的中心频率为6.2 GHz/8.05 GHz，3-dB相对带宽分别为5.6%和2.3%，插入损耗为1.5/2.4 dB。
图 10 (a) 滤波器的实物，(b)测试结果与仿真结果的对比Figure 10. The filter fabricated and comparison between simulated and measured results4. 结论
在本文中，我们基于新型四模谐振器设计了中心频率为6.2/8.05 GHz的双通带带通滤波器。经过理论分析和仿真验证，得到该谐振器的谐振频率均可以被独立调节。滤波器两个通带的Qe可以通过改变馈线的参数来独立控制，所以带宽也可以被独立调节。分析了传输零点产生的原因，从而更好的调节传输零点的位置，提高滤波器的选择性。非谐振节点的引入，提高了滤波器的阻带抑制以及两个带间隔离度。经过仿真，加工和测试，测试结果与仿真结果基本吻合，表明之前分析的正确性。
-
图 1 (a) 四模谐振器的结构, (b)偶模等效电路, (c)奇模等效电路
Figure 1. Structure and equivalent circuits of quad-mode resonator (QMR)
图 2 (a) feve1的场分布; (b) fodd1的场分布; (c) feve2的场分布; (d) fodd2的场分布
Figure 2. Field distribution of four resonating modes
图 7 传输零点随参数的变化
Figure 7. Variation of the transmission zeros (TZs) with varied parameters
图 8 蚀刻DGS与不蚀刻DGS的对比
Figure 8. Comparison of filter response with defected ground structure (DGS) and without DGS
图 10 (a) 滤波器的实物，(b)测试结果与仿真结果的对比
Figure 10. The filter fabricated and comparison between simulated and measured results
表 1 低频通带的耦合矩阵
Table 1. Coupling matrix of low frequency passband
M S 1 2 L S 0 0.022 0.026 0 1 0.022 0.047 0 -0.022 2 0.026 0 -0.045 0.026 L 0 -0.022 0.026 0 
下载: 导出CSV
表 2 高频通带的耦合矩阵
Table 2. Coupling matrix of high frequency passband
M S 3 4 L S 0 0.019 0.036 0 3 0.019 0.051 0 -0.019 4 0.036 0 -0.045 0.036 L 0 -0.019 0.036 0
下载: 导出CSV
表 3 NRN的耦合矩阵
Table 3. Coupling matrix of non-resonant node (NRN)
M S 3 N L S 0 0.895 2 1.112 4 0 3 0.895 2 0.187 3 1.211 5 -0.895 2 N 1.112 4 1.211 5 -19.772 -1.112 4 L 0 -0.895 2 -1.112 4 0
下载: 导出CSV
-
[1] Qiang T, Wang C, Kim N Y. Highly selective dual-wideband bandpass filter using quad-mode resonators for WLAN and WIMAX applications[J]. Microwave & Optical Technology Letters, 2015, 57(6): 1417-1423. [2] Chen Y F, Dai Z J, Chiu C T, et al. Compact dual-band bandpass filter based on quarter wavelength stepped impedance resonators[J]. World Academy of Science, Engineering and Technology, International Journal of Electrical, Computer, Energetic, Electronic and Communication Engineering, 2016, 10(4): 517-520. [3] Wu G, Yang L, Xu Q. Miniaturised dual-band filter with high selectivity using split ring scheme[J]. Electronics Letters, 2015, 51(7): 570-572. doi: 10.1049/el.2015.0318 [4] Gao S S, Sun S, Li J L, et al. Compact dual-mode dual-band bandpass filter with inside-outside-reversed dual-ring topology[J]. Electronics Letters, 2017, 53(9): 624-626. doi: 10.1049/el.2017.0580 [5] Chen J X, Yum T Y, Li J L, et al. Dual-mode dual-band bandpass filter using stacked-loop structure[J]. IEEE Microwave & Wireless Components Letters, 2006, 16(9): 502-504. [6] Zhang Y P, Sun M. Dual-band microstrip bandpass filter using stepped-impedance resonators with new coupling schemes[J]. IEEE Transactions on Microwave Theory & Techniques, 2006, 54(10): 3779-3785. [7] Chuang M L, Wu M T, Tsai S M. Dual-band filter design using L-shaped stepped impedance resonators[J]. IET Microwaves, Antennas & Propagation, 2010, 4(7): 855-0. [8] Liu H, Liu F, Qin F, et al. Compact dual-band HTS bandpass filter using spirally asymmetric stepped-impedance resonators[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-5. [9] Zhang X Y, Chen J X, Xue Q, et al. Dual-band bandpass filters using stub-loaded resonators[J]. IEEE Microwave and Wireless Components Letters, 2007, 17(8): 583-585. doi: 10.1109/LMWC.2007.901768 [10] Yang S, Lin L, Chen J, et al. Design of compact dual-band bandpass filter using dual-mode stepped-impedance stub resonators[J]. Electronics Letters, 2014, 50(8): 611-613. doi: 10.1049/el.2013.4217 [11] Chu Qing Xin, Li, et al. Dual-band filter using asymmetrical stub-loaded resonator with independently controllable frequencies and bandwidths[J]. Let Microwaves Antennas & Propagation, 2013, 7(9): 729-734. [12] Zhou K, Zhou C, Wu W. Substrate integrated waveguide dual-band filter with wide-stopband performance[J]. Electronics Letters, 2017, 53(16): 1121-1123. doi: 10.1049/el.2017.1556 [13] Azad A R, Mohan A. Substrate integrated waveguide dual-band and wide-stopband bandpass filters[J]. IEEE Microwave & Wireless Components Letters, 2018, PP(99): 1-3. [14] Zhou K, Zhou C X, Wu W. Resonance characteristics of substrate-integrated rectangular cavity and their applications to dual-band and wide-stopband bandpass filters design[J]. IEEE Transactions on Microwave Theory & Techniques, 2017(99): 1-14. [15] Gao L, Zhang X Y. High-selectivity dual-band bandpass filter using a quad-mode resonator with source-load coupling[J]. IEEE Microwave and Wireless Components Letters, 2013, 23(9): 474-476. doi: 10.1109/LMWC.2013.2274995 [16] Peng Y, Zhang L, Zheng Z, et al. High selective compact dual-band filter using ring resonator with quarter-wavelength stubs[J]. Electronics Letters, 2017, 53(24): 1589-1591. doi: 10.1049/el.2017.3451 [17] Peng Y, Zhang L, Fu J, et al. Compact dual-band bandpass filter using coupled lines multimode resonator[J]. IEEE Microwave and Wireless Components Letters, 2015, 25(4): 235-237. doi: 10.1109/LMWC.2015.2400936 [18] Liao C K, Chi P L, Chang C Y. Microstrip realization of generalized Chebyshev filters with box-like coupling schemes[J]. IEEE Transactions on Microwave Theory & Techniques, 2007, 55(1): 147-153. 期刊类型引用(0)
其他类型引用(2)
-
下载:
点击查看大图
计量
- 文章访问数: 1230
- HTML全文浏览量: 309
- PDF下载量: 102
- 被引次数: 2
