基于Christopherson迭代的超精密加工流场分析方法

杨航; 马登秋; 张强; 刘小雍; 樊炜; 张云飞; 黄文; 何建国

doi:10.11884/HPLPB201931.180373

基于Christopherson迭代的超精密加工流场分析方法

doi: 10.11884/HPLPB201931.180373

杨航^{1, 2,},
马登秋¹,
张强¹,
刘小雍¹,
樊炜^{3, 4},
张云飞³,
黄文^{3, 4},
何建国³

1.
遵义师范学院工学院，贵州遵义 563006
2.
国防科技大学智能科学学院，长沙 410073
3.
中国工程物理研究院机械制造工艺研究所，四川绵阳 621900
4.
中国工程物理研究院超精密加工技术重点实验室，成都 610200

基金项目:

贵州省教育厅青年科技人才成长项目黔教合KY字[2017]249

贵州省科技计划项目黔科合LH字[2017]7081

教育部重点实验室开放基金课题项目黔教合KY字[2017]385

国家自然科学基金项目 61605182

详细信息

作者简介:
杨航(1989—)，男，博士研究生，讲师，主要从事超精密加工装备技术与工艺理论研究；yhangde@mail.dlut.edu.cn

中图分类号: TH164
计量
- 文章访问数: 837
- HTML全文浏览量: 158
- PDF下载量: 71
- 被引次数: 0
出版历程
- 收稿日期: 2018-12-20
- 修回日期: 2019-02-21
- 刊出日期: 2019-07-15

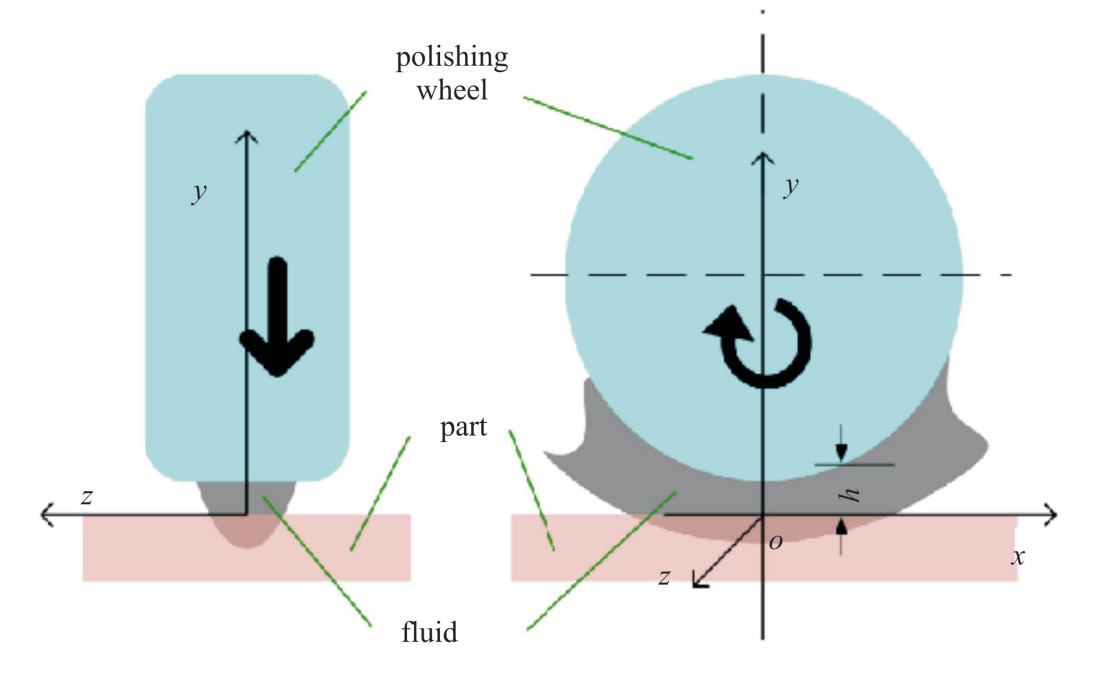
Novel fluid field analysis method for ultra-precision machining based on christopherson iteration

Yang Hang^{1, 2
,},
Ma Dengqiu¹,
Zhang Qiang¹,
Liu Xiaoyong¹,
Fan Wei^{3, 4},
Zhang Yunfei³,
Huang Wen^{3, 4},
He Jianguo³

1.
Dept. of Engineering, Zunyi Normal College, Zunyi 563006, China
2.
Department of Intelligent Technology, National University of Defense Technology, Changsha 410073, China
3.
Institute of Mechanical Manufacturing Technology, CAEP, Mianyang 621900, China
4.
Key Laboratory of Ultra-precision Machining Technology, CAEP, Chengdu 610200, China

摘要

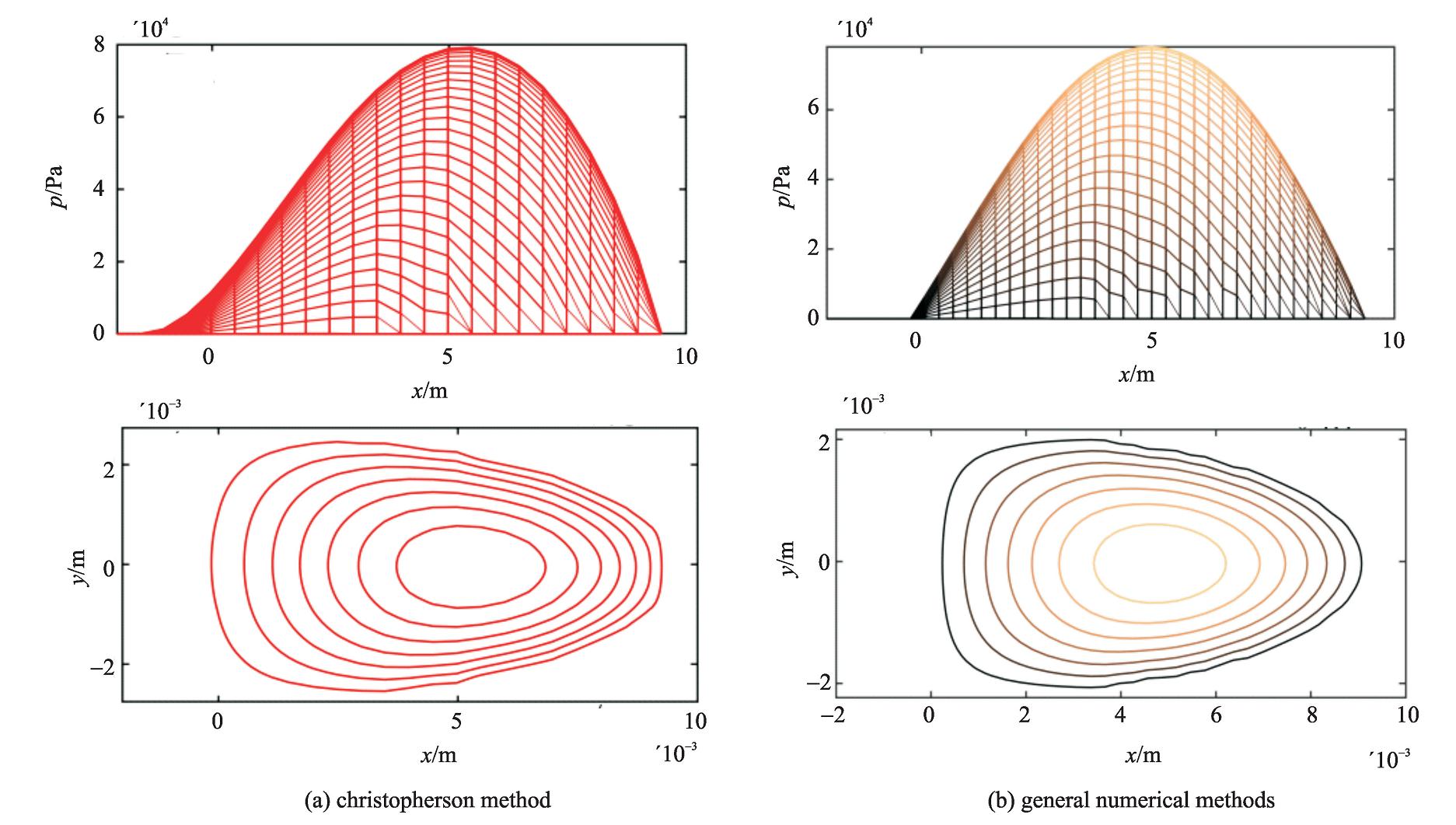
摘要: 随着特种超精密加工技术的发展，复杂流体被越来越多地用于超精密加工工艺中。超精密加工流场分析具有几何特征复杂、流体本构特性多样、流体边界为自有边界等特点，传统流体数值分析方法难以实现可靠分析。从流体的一般特性出发，将D. G. Christopherson提出的非负二阶偏微分系统的超松弛迭代方法用于超精密加工流场分析，建立了适应性与可靠性兼顾的流场分析方法。以磁流变抛光为例，开展了抛光区域压力场数值计算，结果表明所得压力分布形态正确，且分布从x轴正半轴延伸到负半轴，与郑立功等人的实验测定结果一致。另外，基于Kistler力传感器对磁流变抛光过程的法向压力在0.1~0.3 mm浸深段进行了在位测量，发现计算与实验结果偏差均小于20%。表明了该方法的有效性与准确性。
- 超精密加工 /
- 流场分析 /
- Christopherson迭代 /
- 磁流变抛光 /
- 超松弛迭代方法
Abstract: With the development of ultra-precision machining technology, complex fluid is increasingly utilized. The analysis of ultra-precision machining fluid field is characterized by complex geometry, diverse constitutive equation and free boundary flow, which results in unsatisfactory analysis if adopting traditional numerical method. Based on general characteristic of fluid field, a robust and widely adaptable fluid analysis method is proposed in this paper by applying D. G. Christopherson's super-relaxation iterative method for nonnegative second order partial differential systems to ultra-precision machining fluid field analysis. Besides, taking magnetorheological finishing as an example, the numerical calculation of pressure field is conducted for the polishing area and it is revealed that the calculated pressure distribution has reasonable morphology and it extends from positive x axis to negative x axis, which agrees with the experiment results by Zheng Ligong et al. Moreover, the in-situ experimental measurement of normal pressure by Kistler sensor is conducted for immersion depth ranging over 0.1 to 0.3 mm, it is demonstrated that the relative errors of calculations against experimental results are all less than 20%, indicating that the proposed method is valid and accurate.
- ultra-precision machining /
- fluid field analysis /
- Christopherson iteration /
- magnetorheological finishing /
- super-relaxation iterative method

HTML全文

图 1 Bingham模型的同伦曲线变化关系图示

Figure 1. Schematic diagram of homotopy curve variation of Bingham model

下载: 全尺寸图片幻灯片

图 2 磁流变抛光区域流场参数定义

Figure 2. Definition of flow field parameters in magnetorheological finishing area

下载: 全尺寸图片幻灯片

图 3 压力场计算结果对比

Figure 3. Comparison of pressure field calculation results

下载: 全尺寸图片幻灯片

图 4 采用Kistler传感器在位测量磁流变抛光过程的压力

Figure 4. In-situ measurement of the pressure during the magnetorheological finishing process with a Kistler sensor

下载: 全尺寸图片幻灯片

图 5 不同浸深下实测磁流变抛光过程压力

Figure 5. The measured pressure of magnetorheological finishing process at different immersion depths

下载: 全尺寸图片幻灯片

表 1 常见磁流变抛光工艺参数

Table 1. Common magnetorheological finishing process parameters

parameters	geometry			kinematics	physics		fluid
parameters	ribbon height H/mm	ribbon width W/mm	wheel diameter D/mm	rotation speed n (r·min)	fluid viscosity μ	fluid density ρ /(kg·m^-3)	critical Reynolds number Re_c
typical value	1.5	4	300	50	720 Pa·s@50s^-1	6000	2300~4000

下载: 导出CSV

参考文献(23)

[1]	Cao Z C, Cheung C F. A study of materials removal mechanisms for fluid jet polishing using computational fluid dynamics modeling[C]//ASPE 2014, 2014: 496-501.
[2]	Hwang Y, HaK G, Kim Y B, et al. Suppression of the inflection pattern in ultraprecision grinding through the minimization of the hydrodynamic force using a toothed wheel[J]. International Journal of Machine Tools and Manufacture, 2016, 100: 105-115. doi: 10.1016/j.ijmachtools.2015.10.009
[3]	Namba Y, Katagiri M. Ultraprecision grinding of potassium dihydrogen phosphate crystals for getting optical surfaces[C]//Proc of SPIE. 1999, 3578: 692-693.
[4]	李智钢, 鲍振军, 朱衡, 等. 多磨头数控抛光对大口径离轴抛物面镜中频误差的抑制[J]. 强激光与粒子束, 2018, 30: 062003. doi: 10.11884/HPLPB201830.170457 Li Zhigang, Bao Zhenjun, Zhu Heng, et al. Suppression of medium frequency error of off-axis parabolic mirror with large diameter by multi-head CNC polishing. High Power Laser and Particle Beams, 2018, 30: 062003 doi: 10.11884/HPLPB201830.170457
[5]	Niu H Y, Zhang X J. Research on computer controlled polishing technology of 124 mm aspheric reaction-burned silicon carbide mirror[J]. Optics and Precision Engineering, 2006, 14(4): 539-544. doi: 10.3321/j.issn:1004-924X.2006.04.003
[6]	李智钢. 计算机数控抛光对大口径离轴抛物面面形PSD的控制[C]//强激光材料与元器件学术研讨会暨激光破坏学术研讨会论文集2016: 312-312. Li Zhigang. Computer numerical control polishing on large diameter off-axis paraboloid shape PSD control //Proceedings of the Symposium on Strong Laser Materials and Components and Laser Damage Symposium. 2016: 312-312
[7]	Liu P, Lin B, Li Y, et al. Liquid film characteristic in fluid hydrodynamic fixed abrasive grinding[J]. International Journal of Advanced Manufacturing Technology, 2018, 96(9): 4205-4214.
[8]	Su Y T, Wang S Y, Chao P Y, et al. Investigation of elastic emission machining process: lubrication effects[J]. Precision Engineering, 1995, 17(3): 164-172. doi: 10.1016/0141-6359(94)00014-Q
[9]	Namba Y, Tsuwa H, Wada R. Ultra-precision float polishing machine[C]//CIRP Annals Manufacturing Technology. 1987: 211-214.
[10]	杨航, 朱正龙, 刘小雍, 等. 通用磁流变抛光斑空间确定性创成方法[J]. 组合机床与自动化加工技术, 2017(3): 53-56. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHJC201703014.htm Yang Hang, Zhu Zhenglong, Liu Xiaoyong, et al. General magnetorheological polishing spot space deterministic creation method. Modular Machine Tools and Automatic Processing Technology, 2017(3): 53-56 https://www.cnki.com.cn/Article/CJFDTOTAL-ZHJC201703014.htm
[11]	Yang H, He J, Huang W, et al. Spot breeding method to evaluate the determinism of magnetorheological finishing[J]. Optical Engineering, 2017, 56(3): 1-6.
[12]	杨航, 何建国, 黄文, 等. 磁流变抛光去除函数获取的微分解耦方法[J]. 强激光与粒子束, 2015, 27: 082005. doi: 10.11884/HPLPB201527.082005 Yang Hang, He Jianguo, Huang Wen, et al. Micro-decomposition coupling method obtained by magnetorheological polishing removal function. High Power Laser and Particle Beams, 2015, 27: 082005 doi: 10.11884/HPLPB201527.082005
[13]	Kanish T C, Narayanan S, Kuppan P, et al. Investigations on the finishing forces in magnetic Field Assisted Abrasive Finishing of SS316L[C]//GCMM. 2017: 611-620.
[14]	Zhang F, Yu X, Zhang Y, et al. Experimental study on polishing characteristics of ultrasonic magnetorheological compound finishing[C]// ISAAT. 2009: 235-239.
[15]	Cao Z C, Cheung C F. Theoretical modelling and analysis of the material removal characteristics in fluid jet polishing[J]. International Journal of Mechanical Sciences, 2014, 89: 158-166. doi: 10.1016/j.ijmecsci.2014.09.008
[16]	施春燕, 袁家虎, 伍凡, 等. 射流抛光多相紊流流场的数值模拟[J]. 强激光与粒子束, 2009, 21(1): 6-10. http://www.hplpb.com.cn/article/id/3822 Shi Chunyan, Yuan JiaHu, Wu Fan, et al. Numerical simulation of jet polishing multiphase turbulent flow field. High Power Laser and Particle Beams, 2009, 21(1): 6-10 http://www.hplpb.com.cn/article/id/3822
[17]	Hoyng C. New MRF fluid focuses in on 1Å roughness[J]. Laser Focus World, 2014, 50(8): 53-58.
[18]	Ranjan P, Balasubramaniam R, Jain V K. Analysis of magnetorheological fluid behavior in chemo-mechanical magnetorheological finishing (CMMRF) process[J]. Precision Engineering, 2017, 49: 122-135.
[19]	Das M, Jain V K, Ghoshdastidar P S. A 2D CFD simulation of MR polishing medium in magnetic field-assisted finishing process using electromagnet[J]. International Journal of Advanced Manufacturing Technology, 2014, 76(1/4): 173-187.
[20]	Ji S M, Ge J Q, Tan D P, et al. Three-phase abrasive flow polishing and distribution characteristics of bubble collapse[J]. Optics and Precision Engineering, 2018, 26(2): 388-398.
[21]	Christopherson D G. The relaxation method in stress analysis[J]. British Journal of Applied Physics, 2002, 3(3): 65.
[22]	Cryer C W. The method of Christopherson for solving free boundary problems for infinite journal bearings by means of finite differences[J]. Mathematics of Computation, 1971, 25(115): 435-443.
[23]	Zheng Ligong, Li Longxiang, Wang Xiaokun, et al. Coordinate-origin calibration of removal function in Magnetorheological finishing[J]. Optics and Precision Engineering, 2017, 25(1): 8-14.