Equivalent parameters prediction of dielectric barrier discharge piecewise model with parallel ceramic rods
-
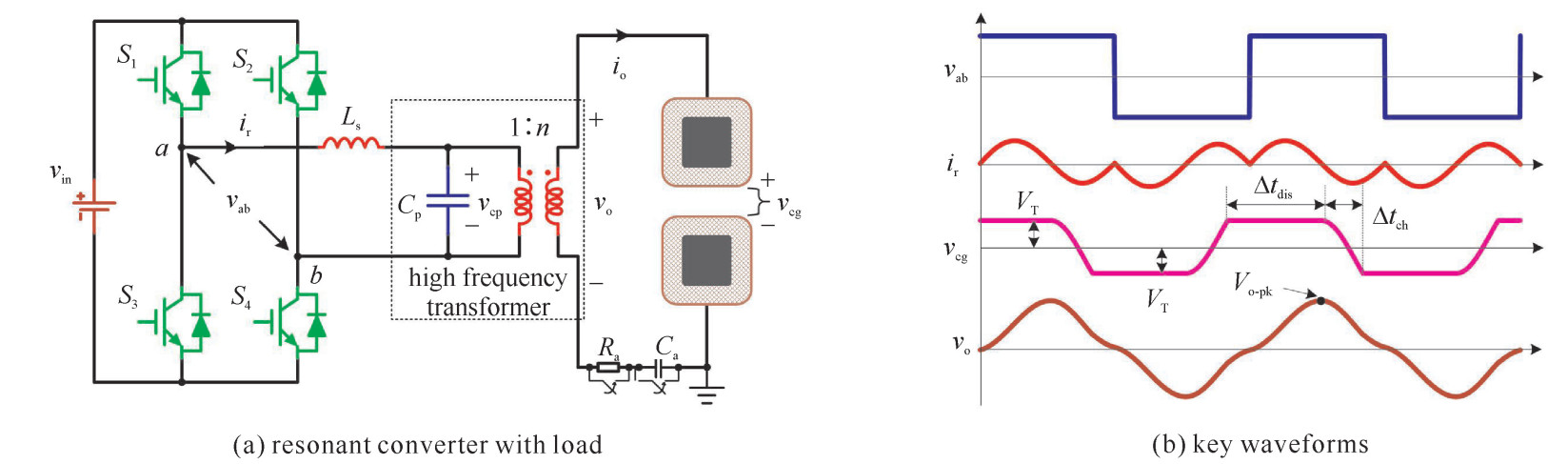
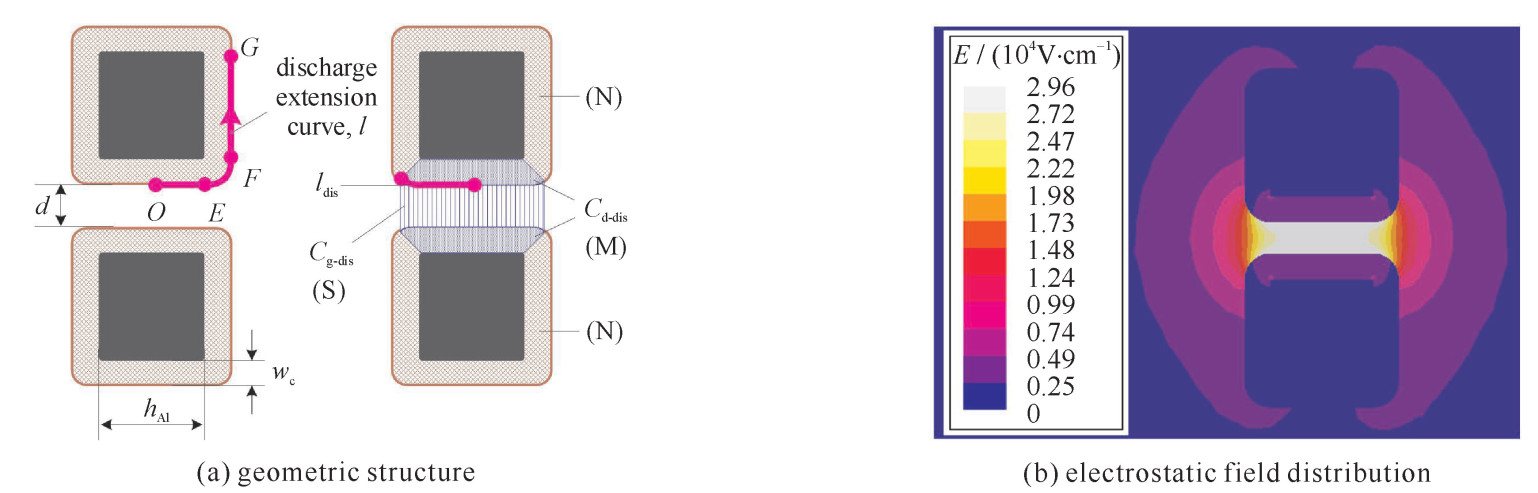
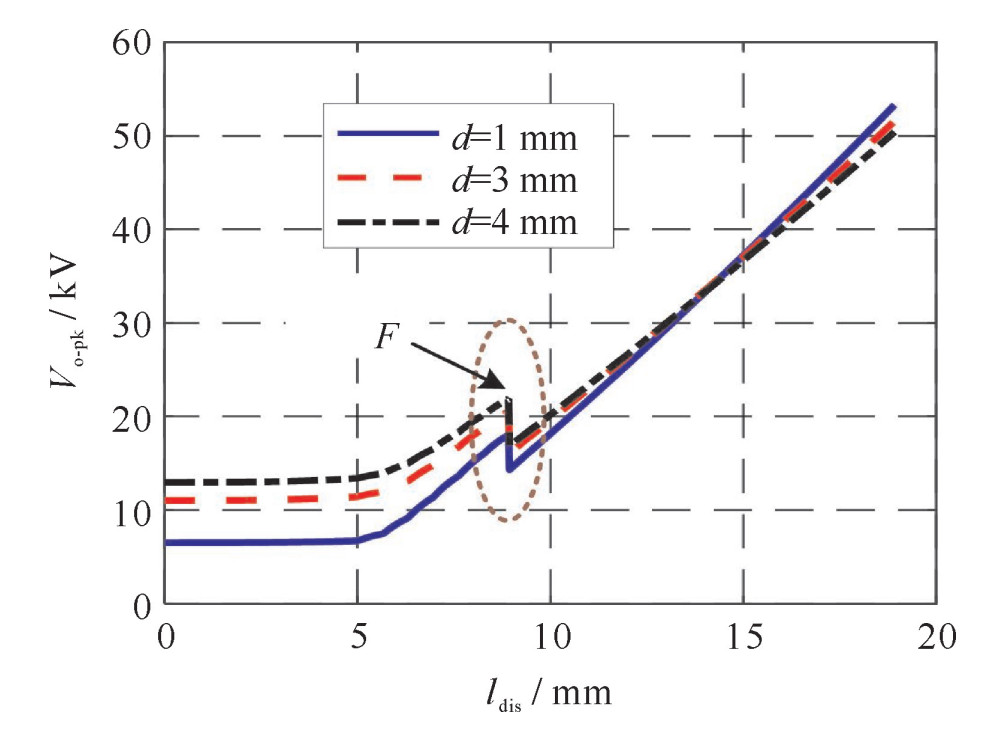
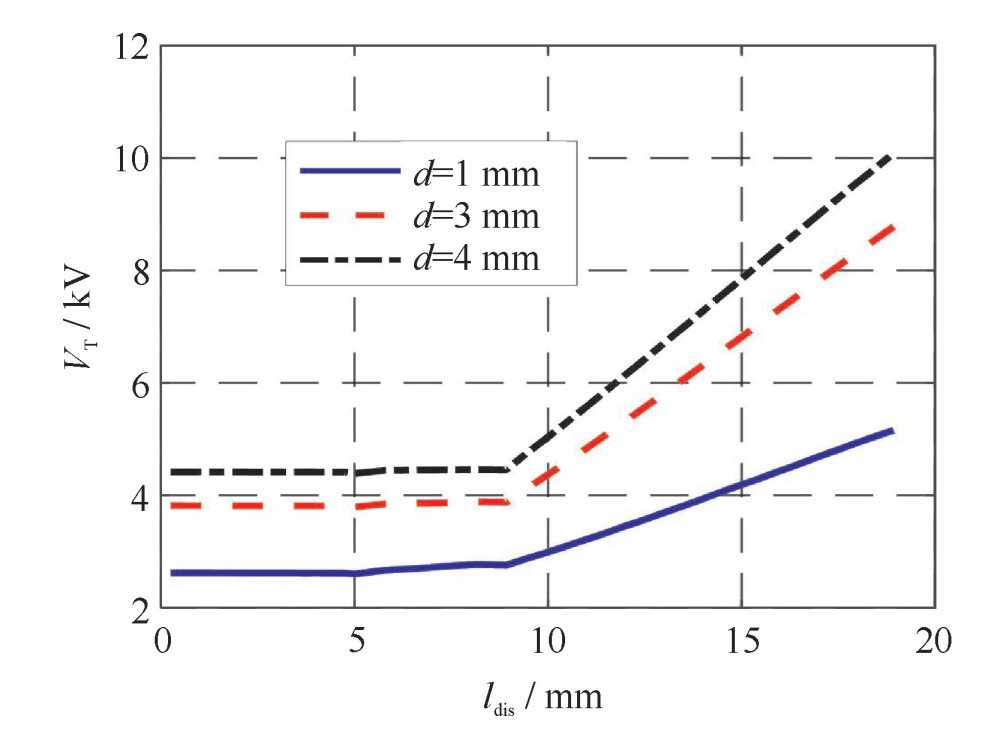
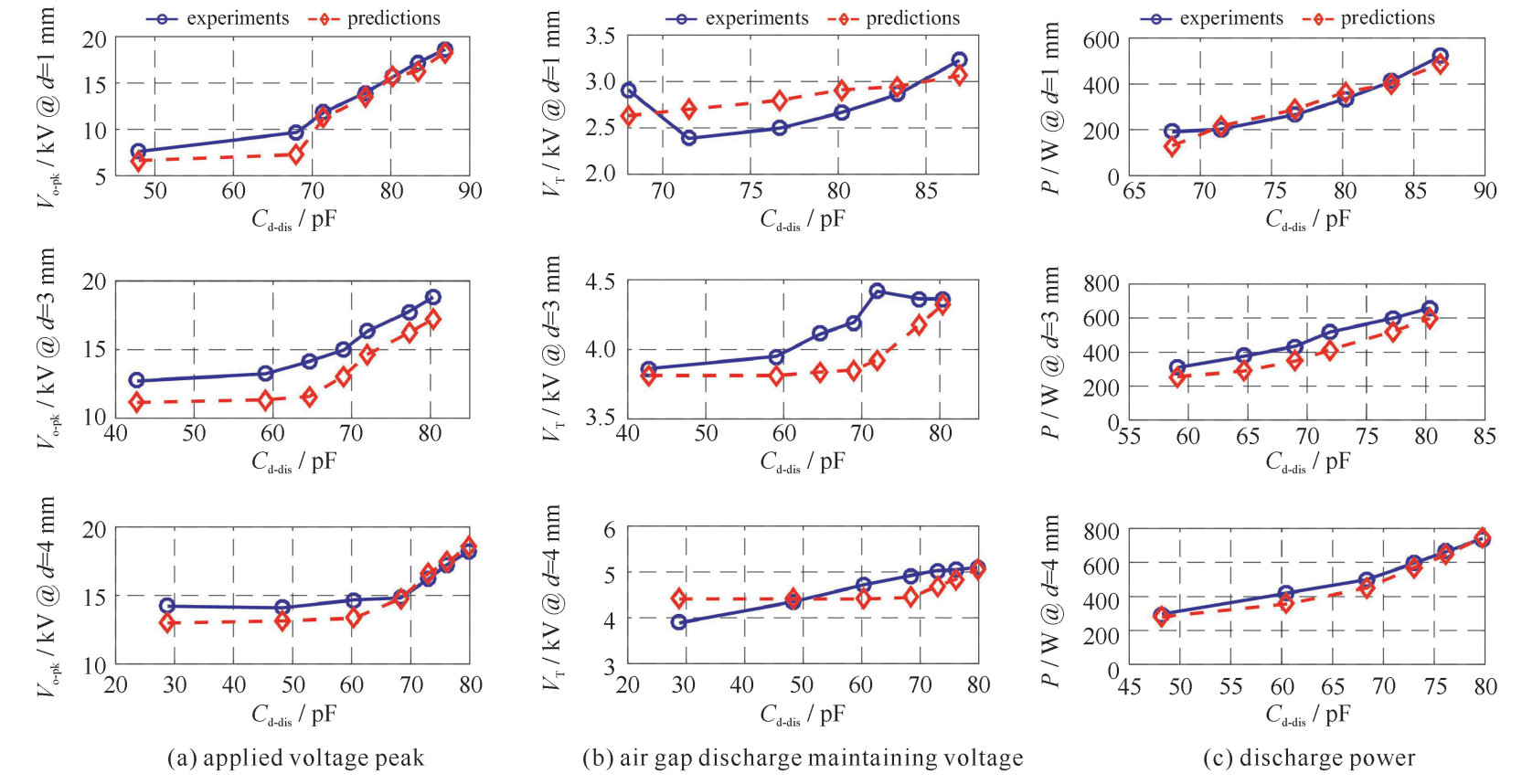
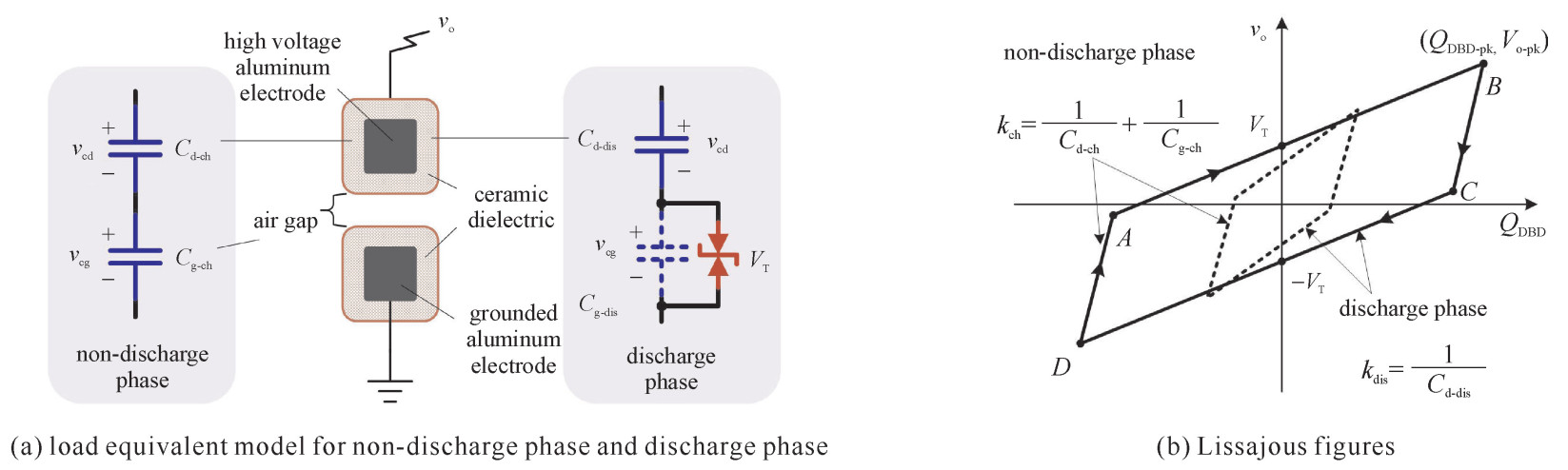
摘要: 为实现对介质阻挡放电负载模型等效参数的有效预测，引入放电区域面积作为中间变量。以平行陶瓷棒为负载，通过Maxwell有限元仿真得到恒压静电场下的负载等效电容与放电区域的对应关系。结合恒压静电场下的电场分布，提出了放电区域逐步扩张下的气隙首次击穿电压、负载外加电压峰值及气隙放电维持电压的预估方法。进而，根据李萨如图形法求得各个工作点的功率。至此，建立起了放电区域同各个等效参数间的量化关系，并实现了对参数的预测。最后，对气隙间距为1，3，4 mm的工况进行了实验验证。实验结果表明：气隙放电维持电压预测值在局部变化趋势上与实测值存在一定差异；放电功率、负载外加电压峰值预测结果与实测值较为吻合。Abstract: In order to achieve effective prediction of the equivalent parameters of dielectric barrier discharge piecewise model, discharge region is introduced as an intermediate variable in the proposed method. In this study, taking parallel ceramic rods as the reactor, the corresponding relationships between the equivalent capacitances of the reactor and the discharge region are obtained by Maxwell finite element simulation under constant voltage electrostatic field. With the help of electric field distribution, the estimation theories of how the critical parameters change over the gradual expansion process of the discharge region are explained, including the air gap first breakdown voltage, the peak value of the applied voltage and the air gap discharge maintaining voltage. Afterwards, the discharge power under various operating conditions can be calculated by Lissajous's figure method. Thus the quantitative relationship between the discharge region and each equivalent parameter is established, and the prediction is realized. An experiment for verification was performed with air gap distances of 1 mm, 3 mm, and 4 mm. It is shown that the predicted and the experimental curves of discharge maintaining voltage have some difference in the local variation trend, while the discharge power and the applied voltage peak prediction results are in good agreement with the measured ones.
-
半导体器件广泛存在于各种现代设备中，其组成的电子系统面临着复杂电磁环境如高强电磁辐射、电离辐射等的直接威胁。基于实验的器件效应分析昂贵、费时，且不易分析物理机理。半导体器件仿真软件（TCAD）是进行复杂环境下器件特性分析的一种重要手段，它是建立在半导体物理基础上的数值模拟仿真工具。国内学者采用TCAD对高功率微波作用下的器件特性退化与损伤、电离辐射对器件性能影响等问题进行了很多相关研究[1-8]。半导体器件模拟基于求解电磁-载流子输运耦合方程组，且须解决多介质、复杂边界、非线性多物理耦合等问题。JEMS-CDS-Device基于非结构网格并行框架JAUMIN开发，采用有限体积方法，支持2维和3维器件仿真和相关组件的扩展开发。本文介绍了JEMS-CDS-Device软件的主要架构与关键实现技术及其验证与应用。
1. 物理模型与控制方程
半导体仿真一般需耦合求解三个基本方程：电势泊松方程、电子连续性方程和空穴连续性方程，即
{∇⋅ε∇ψ=−q(p−n+N+D−N−A)−ρs∂n∂t=1q∇⋅Jn−(U−G)∂p∂t=−1q∇⋅Jp−(U−G) (1) 式中：
ε 是介电常数；ψ 是电势；q 是单位电荷量；n 和p 分别是电子和空穴浓度；N−A 和N+D 是杂质离子浓度；ρs 是固定电荷量；Jn 和Jp 分别是电子与空穴电流密度；U和G分别是载流子的生成率与复合率。漂移−扩散输运模型（DDM）是波耳兹曼方程的近似特例，适用于描述较大尺度半导体器件中的载流子输运现象[9-11]
{Jn=qμnnEn+qDn∇nJp=qμppEp−qDp∇p (2) 式中：
μn 与μp 分别是电子与空穴的迁移速率；Dn=(kBT/q)μn,Dp=(kBT/q)μp ，kB是玻耳兹曼常数，T为温度；En 和Ep 是电子和空穴受到的有效电场强度，考虑到能带变化等效应[10]，可表示为{En=1q∇(−qψ−χ−ΔEc)−kBTq∇(lnNc−lnT3/2)Ep=1q∇(Ec−Eg+ΔEv)+kBTq∇(lnNv−lnT3/2) (3) 式中：
ψ 是电势；χ 是电子亲和能；Ec 是导带底能级；Eg 是能隙；ΔEc 和ΔEv 是重掺杂或压力引起的能带偏移；Nc 和Nv 是态密度。如考虑温度等效应，还需与热传导方程等耦合求解[10]
ρcP∂T∂t=∇⋅κ∇T+J⋅E+(Eg+3kBT)(U−G) (4) 式中：
cP 和ρ 分别为材料的比热容和密度；κ 为热导率；公式中右侧第二项为欧姆热，其中，J 为电流密度矢量，E 为电场；第三项为载流子复合与生成导致的放热与吸热，其中，U为载流子复合率，G为载流子电离率。考虑到热效应，载流子扩散电流Jn,diff 和Jp,diff 应分别表达为[10]{Jn,diff=μnkB(T∇n+n∇T)Jp,diff=−μpkB(T∇p+p∇T) (5) 控制方程组改写为[10]
{∂n∂t=∇⋅(μnnEn+μnkBTq∇n+μnkB∇Tqn)−(U−G)∂p∂t=−∇⋅(μppEp−μpkBTq∇p−μpkB∇Tqp)−(U−G)∇⋅ε∇ψ=−q(p−n+N+D−N−A)−ρsρcP∂T∂t=∇⋅κ∇T+J⋅E+(Eg+3kBT)(U−G) (6) 迁移率与载流子有效质量和被散射几率有关[11]。迁移率模型分为弱场模型、强场模型和表面模型，一般是载流子浓度、场强和温度等相关的非线性函数。常见的有Analytic模型、Philips模型和Lucent模型等[10]。载流子复合模型一般由SRH复合、Auger复合和直接复合三种机制组合而成[9-11]。载流子生成率模型一般考虑碰撞电离效应和能带间隧道跃迁两种机制[9-11]。
2. 数值方法与技术
2.1 数值离散方法
器件的三个控制方程皆可写为如下守恒形式
∂Yi∂t−∇⋅JYi+RYi=0 (7) 为保证守恒性，一般采用有限体积法离散此方程。程序采用顶点型有限体积法（CV-FVM），在原网格上进行场离散与通量插值，在对偶网格（外心型，如图1所示）上进行积分。方程两边对控制体Ci积分，并使用高斯公式将散度体积分转换为通量的表面积分，即[12]
∫Ci∂Yi∂tdV−∫∂CiJYi⋅ndS+∫CiRYidV=0 (8) 载流子输运问题通常是一种对流占优问题，一般需要采用迎风离散格式保持计算稳定。半导体模拟通常使用Scharfetter-Gummel离散格式（SG）离散电流，SG格式是一种自适应权重迎风格式。不考虑温度变化时，基于漂移-扩散模型（DDM）的电流通量密度SG格式可以表示为[9-10]
{Jn|mid=qVTlμn|mid[njB(ψj−ψiVT)−niB(ψi−ψjVT)]Jp|mid=qVTlμp|mid[piB(ψj−ψiVT)−pjB(ψi−ψjVT)]B(x)=xex−1 (9) 式中：
Jn|mid 和Jp|mid 分别表示棱边中点的电子与空穴电流密度；VT=kBT/q 为热电压常数；l 为棱边长度；n，p为节点上的电子、空穴，下标i，j表示一条棱边上的两个节点编号。为考虑温度变化的SG电流密度离散公式较为复杂，可参考文献[10]。半导体方程离散后，采用全耦合牛顿法直接求解非线性方程组，对于
F(x)=0 [13]，有{J(xk)Δxk=−F(xk)xk+1=xk+Δxk (10) 式中：k表示迭代步。对于瞬态求解，半导体方程稳定时间步长一般远小于模拟总时间，故时间离散一般采用隐式欧拉法。
2.2 数值技术
2.2.1 自动微分技术
牛顿法需建立Jacobia矩阵，其计算难度以平方比例增长。自动微分技术起源于Bill Gear的论文[14]，其原理基于复合函数链式求导法则，可以获得偏导数的数值精确解，示例如图2所示。
2.2.2 载流子密度修正
在牛顿法迭代过程中，载流子密度可能出现负值（载流子密度物理上不小于0），负密度易引起牛顿迭代发散，需引入密度修正[10]
ρc={ρc,ρc>0ε(ρc),ρc⩽0 (11) 式中：ρc为电子或空穴载流子密度；
ε(ρc) 为远小于ρc量级的一个正数。2.2.3 积分网格修正
CV-FVM方法对网格有一定要求，当原网格单元为含有钝角的非Delaunay网格或在边界上存在含有钝角的Delaunay网格时，其对偶网格会产生“负体积”，并引起积分错误，如图3所示。程序中需对积分网格按单元进行截断修正[15]。
2.2.4 间断型边界处理
器件仿真中存在大量的间断型边界，间断型边界一般出现在两种不同材料的界面处，如金属-半导体界面、异质半导体界面、辐射问题中的SiO2-Si界面。物理量在边界处不连续，出现了“跳跃”，如图4(a)所示。程序中在界面物理节点处引入了额外的逻辑节点[15]，用于区分不同算法区域，如图4(b)所示。
图 4 异质界面处的间断与算法区域处理Figure 4. Discontinuity heterogeneous interface and algorithm region processing (right figure, there are two logical nodes M1 and M2 in node A)2.2.5 方程求解与预条件技术
半导体DD模型全耦合生成的Jacobia矩阵为稀疏带状，且一般为非对称、强多尺度。此类型问题求解一般需采用直接法（LU）或使用“ILU类预条件＋Krylov迭代”[16]。表1为某2维PN器件生成的线性方程串行求解时线性解法器收敛情况对比，每次加密后未知量增加到原来的4倍。计算规模较小的情况下，直接法速度较快。表1中时间后的括号中为线性解法器迭代次数（直接法LU迭代次数为1）。
表 1 DDM1非线性迭代中线性解法器典型收敛情况）Table 1. Typical convergence of linear solver in DDM1 nonlinear iterationlinear solver precondition time （iterations）/s mesh refinement 0;
DOF: 11 165mesh refinement 1;
DOF: 43 925mesh refinement 2;
DOF: 174 245mesh refinement 3;
DOF: 694 085LU − 0.209 6 (1) 1.065 2 (1) 7.018 4 (1) 50.442 3 (1) BiCGSTAB Jacobi 0.131 8 (106) 0.868 3 (226) 7.119 6 (455) 68.205 1 (1 011) BiCGSTAB ASM 0.126 5 (106) 0.919 0 (226) 7.666 1 (455) 72.558 4 (1 011) BiCGSTAB ILU 0.127 6 (106) 0.840 7 (226) 7.020 5 (455) 69.624 0 (1 011) GMRES BJacobi 0.263 5 (448) 2.358 7 (940) 26.995 4 (2 548) 427.814 (9 450) GMRES ASM 0.291 4 (448) 2.466 6 (940) 27.758 8 (2 548) 462.929 (9 450) GMRES ILU 0.283 8 (448) 2.311 4 (940) 27.126 1 (2 548) 425.375 450) 3. 软件架构与实现
JEMS-CDS-Device并行基于JAUMIN并行计算框架实现，该框架由北京应用物理与计算数学研究所研制。JAUMIN采用网格层-网格片-单元的分布式网格管理结构（图5），使用并行构件搭建计算流程，构件遍历网格片并调用网格片数值子程序完成计算，用户需实现网格片策略类中特定函数来实现构件功能定制[17-19]。JEMS-CDS-Device计算结果的后处理绘图由TeraVAP[20-21]软件完成，软件输入网格生成使用到了SuperMesh[22-23]程序。
JEMS-Device基于离散中台DDMS构建，主要层次关系如图6所示。DDMS主要由内核与特征功能库两部分组成。内核包含数据模型、算法框架及方程构件。方程构件集成了各组件，并对外提供了统一的接口。算法框架定义了时间积分、非线性FVM求解、流程控制等的算法框架（模板）及接口。数据模型提供了器件结构的抽象描述和相关数据的存储。物理模型库中提供了常用材料的能带、迁移率等的计算模型，并通过统一的接口被算法调用。方程模板中包含了特定输运模型方程组的数值离散与组装算法，通过加载不同的方程模板，DDMS可以生成用于解决特定输运模型的方程构件。各模块之间的关系如图7所示。
4. 典型测试与应用
4.1 DDM基本模型仿真与验证
基本算例1：3维二极管稳态问题，此算例用于验证仿真程序基本功能。算例器件为在掺杂浓度1015 cm−3的均匀N型Si衬底上注入1019 cm−3受主杂质形成。图8(a)为器件净掺杂密度分布图，器件尺寸为6 μm×3 μm×1 μm，图中器件上面中心区域为阳极，下面为阴极。本算例中采用了Analytic迁移率模型，仿真了器件在0～1 V范围内正偏时的状态，得到了器件阳极的电压-电流关系，并与Genius TCAD软件了对比，结果符合良好，如图8(b)所示。
图 8 3维PN净掺杂密度分布与二极管阳极V-I曲线Figure 8. PN diode ’s density distribution of net doping and anode V-I curve基本算例2：2维NMOS管，此算例用于验证程序对异质间断型边界的处理能力。场效应晶体管（MOSFET）是现代集成电路中的重要器件，一般由金属、氧化物和半导体组成。算例器件为一个μm级工艺的NMOS管，由Si，SiO2和金属三种类型材料组成，仿真时Si-SiO2界面设定存在密度为1010 cm−2的界面电荷，程序中此界面作为间断型边界处理。本算例仿真得到了其平衡态电势分布，并与Genius TAD的仿真进行对比，电势分布结果相符，如图9所示。
图 9 2维NMOS管平衡态电势分布结果对比（电势单位：V，参考零点为无穷远）Figure 9. 2D NMOS equilibrium potential distribution comparison（potential unit: V, the potential reference zero is at infinity）4.2 并行性能测试
2维PN算例，此算例器件为一3 μm×3 μm的Si材质二极管，净掺杂分布如图10(a)所示，测试中对此PN管施加了0.5 V的正向偏压，电子浓度分布如图10（b）所示。线性解法器采用BiCGSTAB，预条件使用ASM。ASM是一种加性区域分解预条件[13]，每个分解区域上单独采用ILU[13, 16]生成子区域预条件。
图 10 2维PN管的净掺杂分布与载流子分布（正向偏压0.5 V）Figure 10. Net doping and carrier distribution of 2D PN device (positive deviation 0.5 V)表2与表3展示了JEMS-CDS-Device的弱扩展测试（保持每核心计算规模近似不变）与强扩展测试（保持总计算规模不变）情况。由表3可知，程序在256核并行强扩展效率为59.1%（32核基准），效率较好。由表2中可知，程序在256核并行时相对4核并行的弱扩展效率为15.7%，效率下降的主要原因在于，随着每次未知量的增多（未知量4倍，并行核数4倍），牛顿迭代每步线性求解需要的平均迭代数也随之增加（约2倍，与未知量数量的平方根成正比[24]）。
表 2 弱扩展并行测试（Basic Newton，ASM＋BiCGSTAB）Table 2. Weak extension parallel test (Basic Newton，ASM＋BiCGSTAB)cores unknowns average iterations time/s efficiency/% 4 1.74×105 154 83.32 100 16 6.94×105 353 151.70 54.9 64 2.77×106 757 285.78 29.1 256 1.11×107 1727 531.19 15.7 表 3 强扩展并行测试（Basic Newton，ASM＋BiCGSTAB，2.771×106未知量）Table 3. Strongly extended parallel test (Basic Newton，ASM＋BiCGSTAB，2.771×106 Unknowns)cores total time/s linear solver time/s speedup efficiency/% 32 470.31 228.44 1.00 100.0 64 284.78 113.67 1.65 82.6 128 157.90 59.20 2.98 74.5 256 99.56 32.31 4.72 59.1 4.3 电热耦合仿真应用
电热耦合仿真通过联立求解基本DDM方程与晶格热传导方程，得到器件在外部激励源作用下的瞬态温度分布。本算例中PIN二极管模型为Si材质的P＋NN＋管，主体为直径约20 μm的柱体，净掺杂峰值绝对值约为9.17×1019 cm−3，采用其过中心截面进行二维仿真。器件两电极均设为欧姆接触型，阳极边界热传导系数取某金属3.17 W·cm−1·K−1，器件后部因截断了部分硅，故阴极导热系数取硅的导热系数1.56 W·cm−1·K−1。载流子迁移率模型采用Philips模型并使用了Caughey-Thomas模型进行了强场修正，复合率使用了SRH, Auger和直接复合机制模型计算，碰撞电离率采用了适用于高温的Valdinoci模型。器件端口激励的波形如图11(a)所示，图11(b)为此激励下7.78 ns时的温度分布情况，局部放大图中可见，PIN管PN结边缘处温度较高(最高707.5 K)，边缘阳极接触部分亦有明显升温，这与实际经验相吻合。
图 11 输入的波形与某时刻PIN的温度分布Figure 11. Input waveform and temperature distribution of PIN (at 7.78 ns)5. 结 论
本文介绍了JEMS-CDS-Device程序的架构与实现。JEMS-CDS-Device基于JAUMIN框架与DDMS中台构建，围绕多介质、多物理、非线性全耦合数值模拟这一需求，主要实现了3方面功能：（1）支持多介质，间断型边界，可用于半导体、导体、绝缘体组成的复杂器件模型，支持典型间断型边界问题的高效计算；（2）材料物理模型可扩展，支持物理模型库扩展开发；（3）基于Newton法与自动微分技术，实现非线性多物理方程全耦合求解。算例验证与并行性能测试的情况表明，JEMS-CDS-Device程序对非线性多物理全耦合问题具备千万未知量、数百CPU核的并行计算能力，可以应用于强电磁脉冲等复杂电磁环境下半导体器件多物理效应机理的研究。
-
图 2 带负载的驱动源电路及DCM与CCM临界工作模式下的关键波形
Figure 2. Resonant converter with load and its key waveforms in the critical mode between DCM and CCM
图 3 负载静电场分布及基于几何结构的参数等效方法示意图
Figure 3. Schematic diagram of electrostatic field distribution and equivalent parameter extraction methods based on geometric structure
图 4 不同气隙间距下，放电阶段模型等效电容同放电区域的关系
Figure 4. Equivalent capacitances versus discharge area with different air gap distances
图 5 放电延伸曲线上不同位置对应的均匀系数
Figure 5. Uniformity coefficient versus different position along the discharge expansion curve
图 6 放电延伸曲线上不同位置对应的气隙电压占比
Figure 6. Air gap voltage versus applied voltage at different position
图 7 放电区域扩张所需外加电压峰值的变化曲线
Figure 7. Relationship between applied voltage peak and the discharge area
图 8 放电扩张到不同位置时的放电维持电压
Figure 8. Discharge maintaining voltage corresponding to different discharge area
图 9 不同气隙间距下负载外加电压峰值、放电维持电压及放电功率的实验值同预测值比较
Figure 9. Experiment and prediction results of applied voltage peak value, gap discharge maintaining voltage, and discharge power with different air gap distances
表 1 不放电阶段不同气隙间距下的的等效电容参数
Table 1. Equivalent capacitances during non-discharge stage with different air gap distances
d/mm Cd-ch/pF Cg-ch/pF Cch/pF Cch-exp/pF 1 120.06 53.79 37.15 36.27 3 142.14 24.47 20.87 23.02 4 148.43 20.30 17.86 21.62 
下载: 导出CSV
-
[1] 宋颖. 大气压非平衡等离子体在杀菌中的应用研究[D]. 大连: 大连理工大学, 2014.Song Ying. Inactivation applications of atmospheric pressure nonequilibrium plasmas. Dalian: Dalian University of Technology, 2014 [2] Kogelschatz U. Dielectric-barrier discharges: Their history, discharge physics, and industrial applications[J]. Plasma Chemistry and Plasma Processing, 2003, 23(1): 1-46. doi: 10.1023/A:1022470901385 [3] 胡小吐. AC/DC流光放电等离子体烟气脱硫实验研究[D]. 北京: 北京交通大学, 2007.Hu Xiaotu. Experimental research of AC/DC streamer plasmas in flue gas desulfurization. Beijing: Beijing Jiaotong University, 2007 [4] Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing[M]. Hoboken: John Wiley & Sons, 2005. [5] 郝世强. 介质阻挡放电的能量压缩机理、实现及优化[D]. 杭州: 浙江大学, 2016.Hao Shiqiang. Mechanism, implementation and optimization of dielectric barrier discharge energy compression. Hangzhou: Zhejiang University, 2016 [6] Kinnares V, Hothongkham P. Circuit analysis and modeling of a phase-shifted pulsewidth modulation full-bridge-inverter-fed ozone generator with constant applied electrode voltage[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1739-1752. doi: 10.1109/TPEL.2010.2042075 [7] Eid A, Takashima K, Mizuno A. Experimental and simulation investigations of DBD plasma reactor at normal environmental conditions[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 4221-4227. doi: 10.1109/TIA.2014.2315496 [8] Guo Tangtang, Liu Xingliang, Hao Shiqiang, et al. Prediction of equivalent electrical parameters of dielectric barrier discharge load using a neural network[J]. Plasma Science and Technology, 2015, 17(3): 196-201. doi: 10.1088/1009-0630/17/3/05 [9] Alonso J M, Valdés M, Calleja A J, et al. High frequency testing and modeling of silent discharge ozone generators[J]. Ozone Science & Engineering, 2003, 25(5): 363-376. [10] 王静, 蔡忆昔, 王军, 等. 介质阻挡放电等效电容的测量与分析[J]. 高电压技术, 2008, 34(2): 264-266, 308. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200802013.htmWang Jing, Cai Yixi, Wang Jun, et al. Measurement and analysis of equivalent capacitance in dielectric barrier discharge. High Voltage Engineering, 2008, 34(2): 264-266, 308 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200802013.htm [11] 王辉, 方志, 邱毓昌, 等. 介质阻挡放电等效电容变化规律的研究[J]. 绝缘材料, 2005, 38(1): 37-40. https://www.cnki.com.cn/Article/CJFDTOTAL-JYCT200501012.htmWang Hui, Fang Zhi, Qiu Yuchang, et al. On the changing of equivalent capacitance in dielectric barrier discharge. Insulating Materials, 2005, 38(1): 37-40 https://www.cnki.com.cn/Article/CJFDTOTAL-JYCT200501012.htm [12] Xiao Dengming. Gas discharge and gas insulation[M]. Heidelberg: Springer-Verlag, 2016. [13] 张红. 高电压技术[M]. 北京: 中国电力出版社, 2009.Zhang Hong. High voltage technique. Beijing: China Electric Power Press, 2009 期刊类型引用(0)
其他类型引用(3)
-
下载:
点击查看大图
计量
- 文章访问数: 835
- HTML全文浏览量: 296
- PDF下载量: 107
- 被引次数: 3
