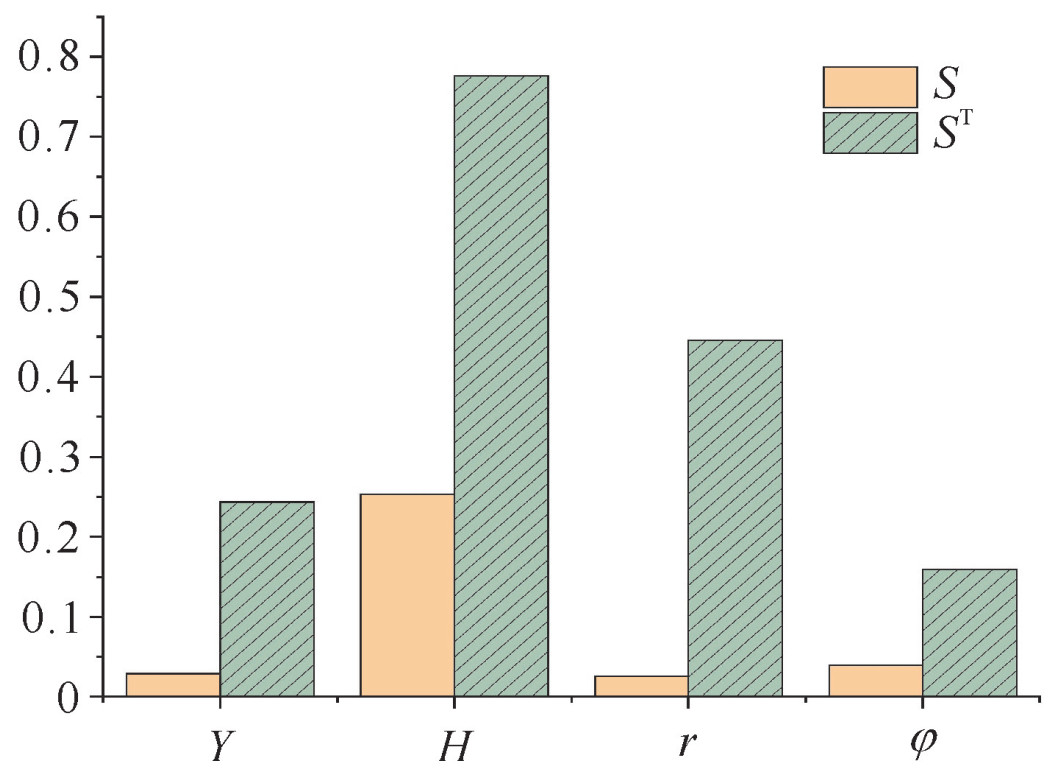Early-time high-altitude electromagnetic pulse simulation and analysis considering parameter uncertainty
-
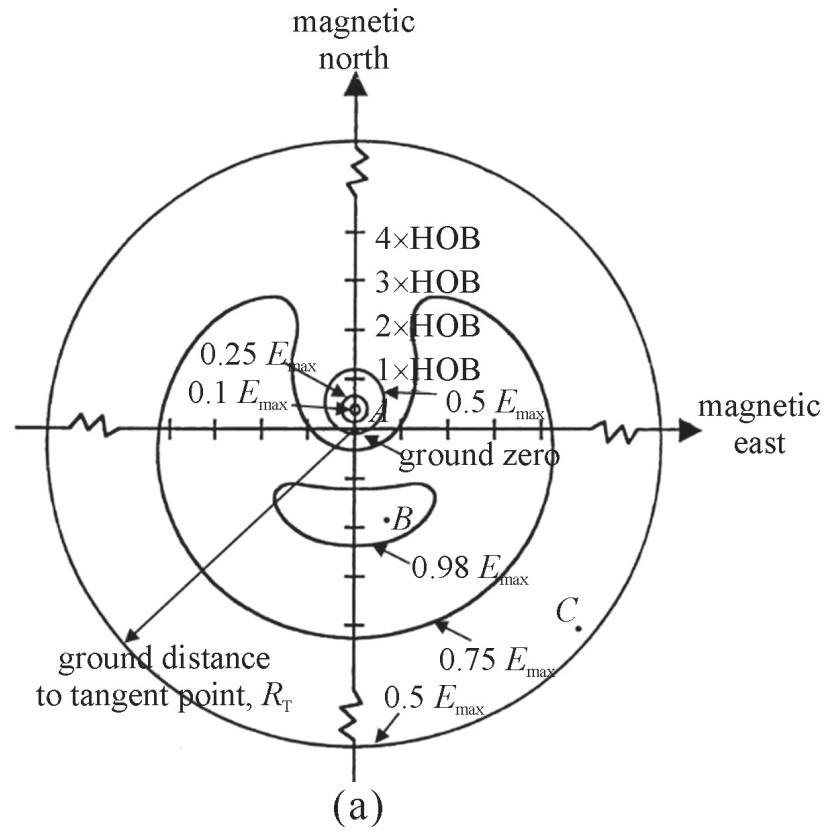
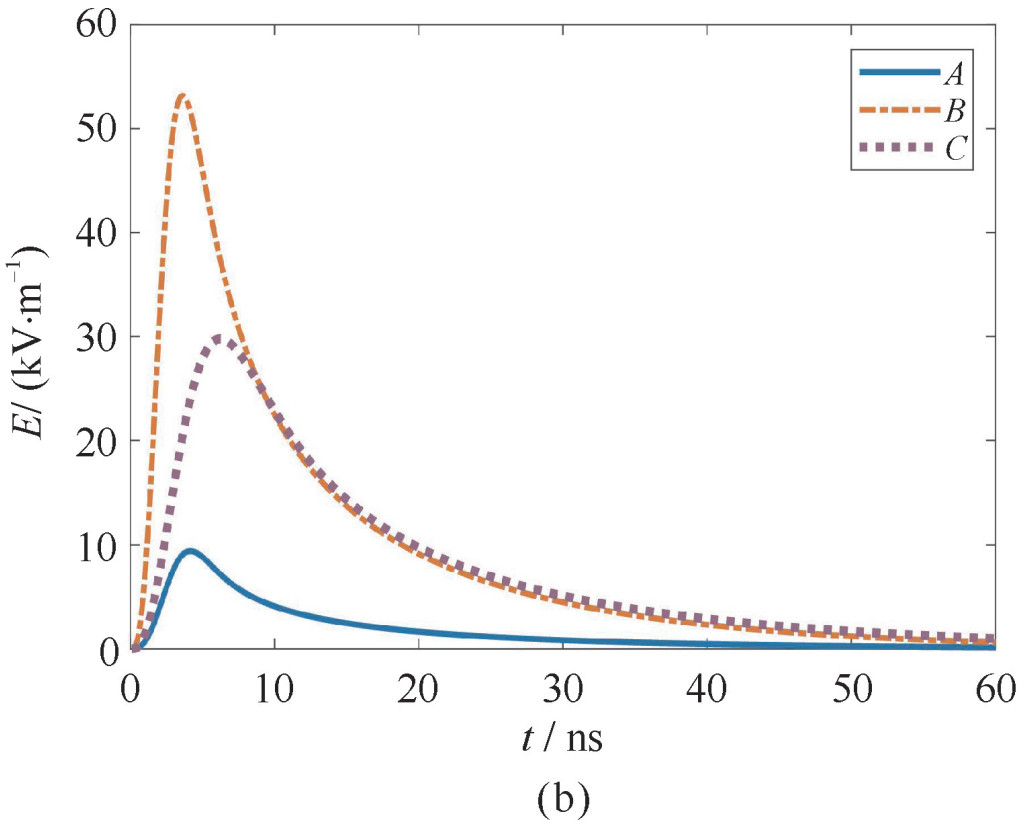
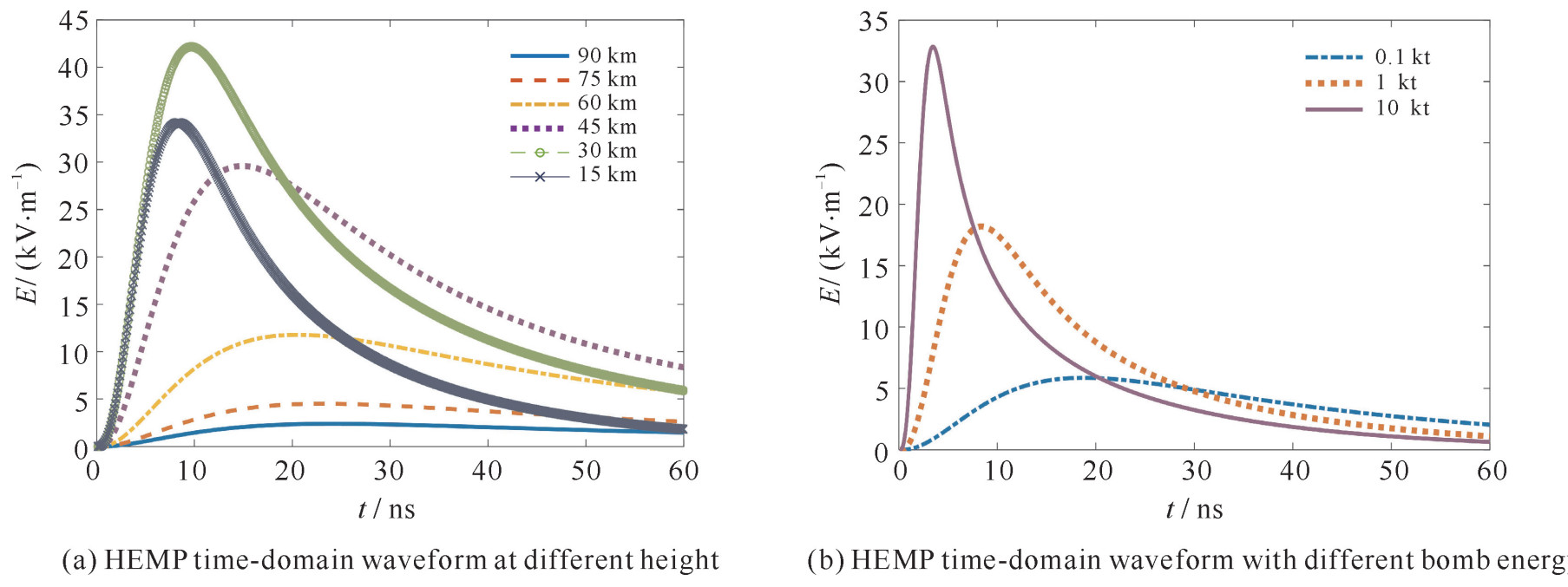
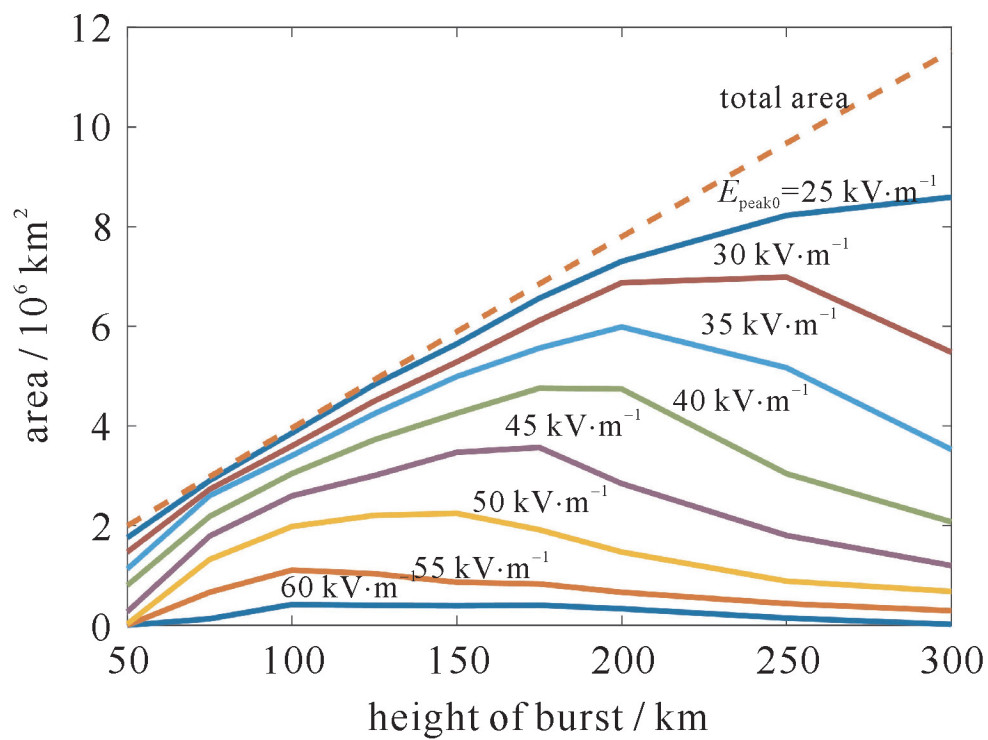
摘要: 高空电磁脉冲的早期分量幅值高、频谱宽、分布范围广，是高空核爆的电磁效应的重要组成部分。分析了国内外高空电磁脉冲早期分量仿真计算法的研究进展，并选取基于高频近似并考虑电子与电磁场自洽作用的EXEMP算法进行详细介绍，通过数值计算结果总结了高空电磁脉冲的时域波形和空间分布随场源当量、爆高等参数变化的规律，与IEC标准约定的波形时域和空间特征一致。针对HEMP计算中部分参数的不确定性，分析参数取值偏差和波动对电磁脉冲计算结果的影响，使用多项式混沌方法联合Sobol全局敏感度指标对其进行不确定量化，得到电磁脉冲关键值可能分布的上下界、分布的概率密度等信息，分析各参数在特定取值范围内对电磁脉冲特征参数的影响及联合影响。Abstract: The early-time high-altitude electromagnetic pulse is an important component of the electromagnetic effect of high-altitude nuclear burst. The relative simulation research work at home and abroad are studied and compared. One of the classical methods EXEMP is introduced in this paper in detail. The numerical result is compared with the IEC reference value of IEC 61000-2-9. The time domain waveform and spatiotemporal distribution of HEMP are studied using numerical result. The influence of burst parameter including energy and height are studied, the uncertainty is quantified by polynomial chaos method and global sensitivity indices.
-
Key words:
- HEMP /
- electromagnetic simulation /
- uncertainty /
- uncertainty quantification
-
图 3 不同高度和不同当量下的电磁脉冲时域波形
Figure 3. HEMP time-domain waveform at different height and bomb energy
图 4 HEMP峰值覆盖面积与场源高度示意图
Figure 4. Area distribution of HEMP amplitude with different burst height
图 5 场源参数主效应敏感度指标和总效应敏感度指标
Figure 5. Main sensitivity indices and global sensitivity indices of burst energy, height and relative distance and direction of observation
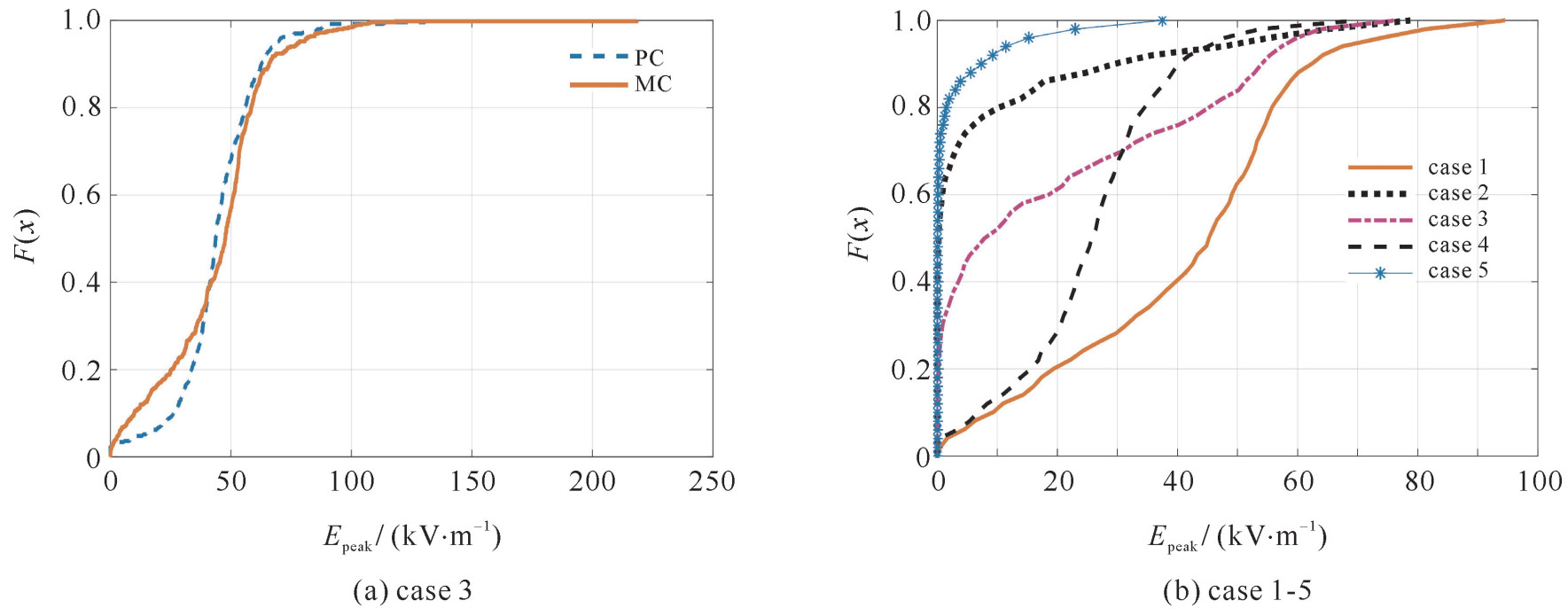
表 1 HEMP算例参数取值范围与全局敏感度指标
Table 1. Parameter range and global sensitivity indices of HEMP simulation cases
H/km r/km φ/rad variable distribution major sensitivity indices total sensitivity indices variable distribution major sensitivity indices total sensitivity indices variable distribution major sensitivity indices total sensitivity indices case 1 h~U[50, 150] 0.163 0.624 $\sqrt{r} \sim U[0, \sqrt{200}]$ 0.160 0.647 φ~U[0, 2π] 0.105 0.256 case 2 h~U[100, 200] 0.321 0.884 $\sqrt{r} \sim U[0, \sqrt{100}]$ 0.051 0.597 φ~U[0, 2π] 0.016 0.117 case 3 h~U[100, 200] 0.180 0.763 $\sqrt{r} \sim U[0, \sqrt{200}]$ 0.120 0.681 φ~U[0, 2π] 0.023 0.209 case 4 h~U[100, 200] 0.100 0.496 $\sqrt{r} \sim U[0, \sqrt{500}]$ 0.347 0.737 φ~U[0, 2π] 0.089 0.164 case 5 h~U[150, 250] 0.202 0.831 $\sqrt{r} \sim U[0, \sqrt{200}]$ 0.106 0.704 φ~U[0, 2π] 0.028 0.120 
下载: 导出CSV
-
[1] Karzas W J. Electromagnetic radiation from a nuclear explosion in space[J]. Phys Rev, 1962, 126(6): 40. [2] Karzas W J, Latter R. Detection of the electromagnetic radiation from nuclear explosions in space[J]. Physical Review, 1965, 137(5B): B1369-B1378. doi: 10.1103/PhysRev.137.B1369 [3] Longmire C. On the electromagnetic pulse produced by nuclear explosions[J]. IEEE Trans Electromagnetic Compatibility, 1978, 26(1): 3-13. [4] Longley H, Longmire C. Development of the CHAP EMP code[R]. 1972. [5] Longmire C. Effect of multiple scattering on the Compton recoil current[J]. Military Technology Weaponry & National Defense, 1978. [6] Longmire C. On the electromagnetic pulse produced by nuclear explosions[J]. IEEE Trans Electromagnetic Compatibility, 1978, 26(1): 3-13. [7] Radasky W A, Knight R L. A two dimensional high altitude EMP environment code[R]. EMP Theor. Notes TN-125, 1971. [8] Ianoz M, Nicoara B I C, Radasky W A. Modeling of an EMP conducted environment[J]. IEEE Trans Electromagnetic Compatibility, 2002, 38(3): 400-413. [9] Leuthäuser K. A complete EMP environment generated by high-altitude nuclear bursts[R]. EMP Theor Notes 363, 1992. [10] Leuthäuser K. A complete EMP environment generated by high-altitude nuclear bursts: Data and standardization[R]. EMP Theor Notes 364, 1994. [11] Leuthäuser K. Distribution functions of the HEMP[R]. EMP Theor Notes 365, 1995. [12] Eng C D. Development of the time dependence of the nuclear (E1) HEMP electric field[J]. IEEE Trans Electromagnetic Compatibility, 2011, 53(3): 737-748. doi: 10.1109/TEMC.2011.2115249 [13] Farmer W A, Cohen B I, Eng C D. On the validity of certain approximations used in the modeling of nuclear EMP[J]. IEEE Trans Nuclear Science, 2016, 63(2): 1259-1267. doi: 10.1109/TNS.2016.2518181 [14] 程引会, 李进玺, 马良. 高空电磁脉冲环境计算中的自洽方法[J]. 计算物理, 2017, 34(4): 403-408. https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201704004.htmCheng Yinhui, Li Jinxi, Ma Liang, et al. Self-consistent method in calculation of high-altitude electromagnetic pulse environment. Chinese Journal of Computational Physics, 2017, 34(4): 403-408 https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201704004.htm [15] 王泰春, 贺云汉, 王玉芝. 电磁脉冲导论[M]. 北京: 国防工业出版社, 2011.Wang Taichun, He Yunhan, Wang Yuzhi. Introduction to electromagnetic pulse. Beijing: National Defense Industry Press, 2011 [16] Cui M. Numerical simulation of the HEMP environment[J]. IEEE Trans Electromagnetic Compatibility, 2013, 55(3): 440-445. doi: 10.1109/TEMC.2013.2258024 [17] Zhang J, Zhang Y R. Using a second-order integral equation method to study the high-altitude nuclear EMP[J]. IEEE Trans Electromagnetic Compatibility, 2018: 1-9. [18] Lee K S H. EMP interaction: Principles, techniques, and reference data[R]. Hemisphere Publishing Corp, 1986. [19] Hoerlin H. United States high-altitude test experiences: A review emphasizing the impact on the environment[R]. 1976. [20] 王建国, 牛胜利, 张殿辉. 高空核爆炸效应参考手册[M]. 北京: 原子能出版社, 2010.Wang Jianguo, Niu Shengli, Zhang Dianhui. Reference manual for high altitude nuclear explosion effects. Beijing: Atomic Energy Press, 2010 [21] IEC 61000-2-9, Electromagnetic compatibility (EMC)—Part 2: Environment—Section 9: Description of HEMP environment—Radiated disturbance[S]. [22] Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathand Comp in Simulation, 2001: 271-280. -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 2244
- HTML全文浏览量: 595
- PDF下载量: 192
- 被引次数: 0
