Power system fault chain simulation model considering effect of geomagnetic storm
-
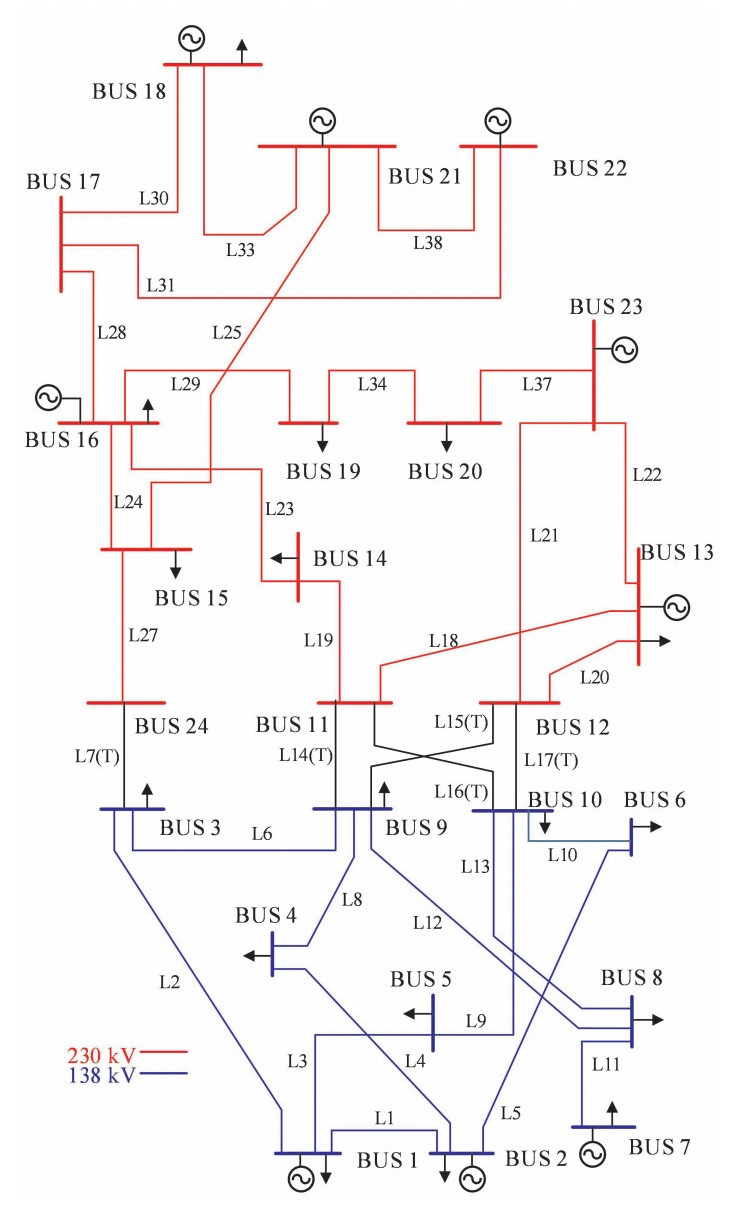
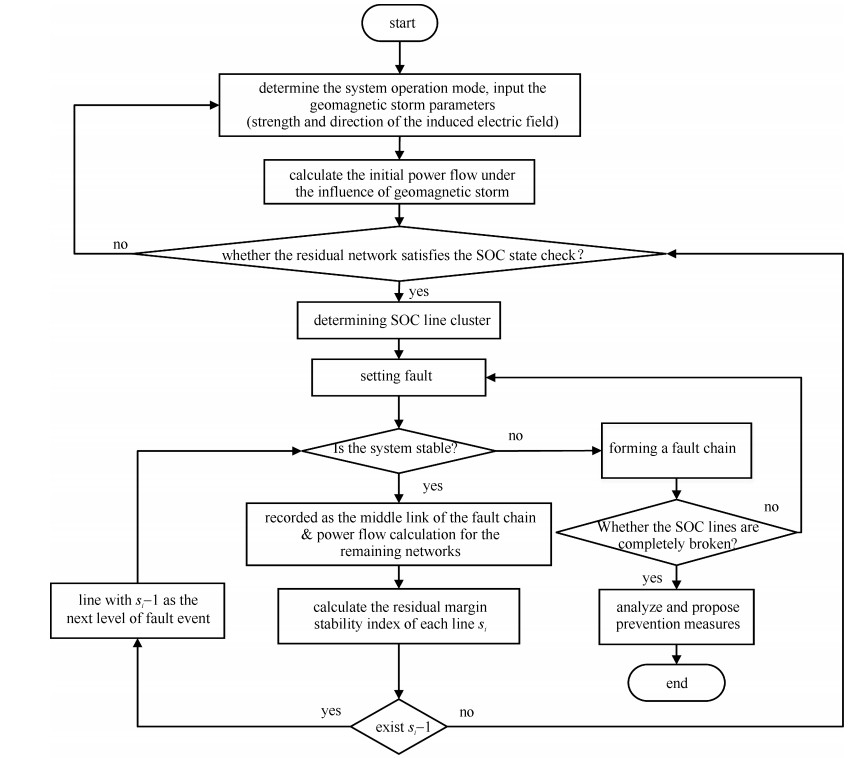
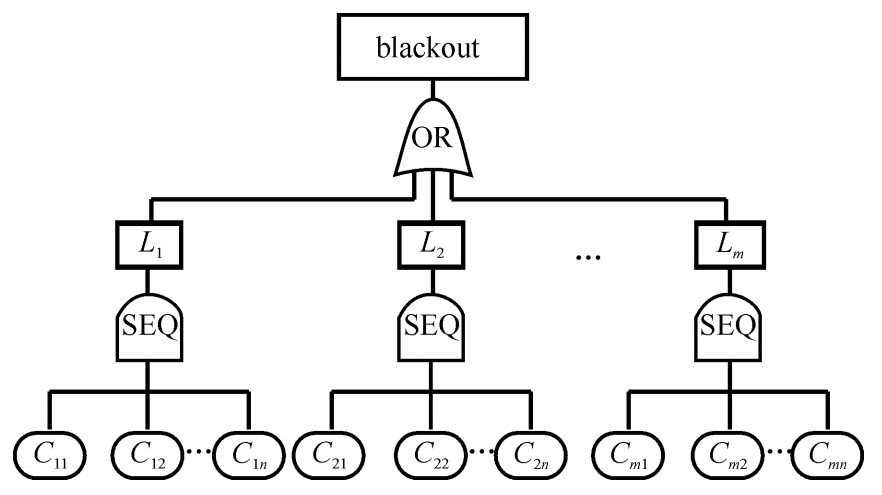
摘要: 地磁暴影响下地磁感应电流(GIC) 流过变压器中性点, 引起变压器无功损耗增加, 在强地磁暴环境中, 系统的无功补偿装置可能过载, 母线电压下降, 可能引发连锁故障, 继而导致大停电事故。对比事故链各环节特点和因磁暴导致的电力系统停电事故的发展规律, 使用事故链模型来仿真实现地磁暴条件下的电网停电过程。基于自组织临界理论和非故障线路的安全稳定裕度来确定连锁故障的传播路径。结合IEEERTS79系统参数, 估算各母线的地理位置, 借助PowerWorld仿真软件, 以该系统为例, 研究结果验证了所提事故链模型可以反映给定电网条件下, 地磁暴参数对电力系统事故链集与薄弱环节辨识的影响, 研究结果可为量化和防治磁暴电网灾害提供依据。Abstract: In the condition of strong magnetic storm, geo-magnetically induced current (GIC) flowing through the neutral point of the transformer, causes the increase of reactive power loss of the transformer.This might lead to overload of the reactive power compensation device, drop of the bus voltage and occurrence of a chain fault, which in turn causes a blackout of the system.Comparing the characteristics of each link in the fault chain and the development law of the power system blackout caused by magnetic storms, the fault chain model is used to simulate the process of power outage under conditions of geomagnetic storm.The article determines the propagation path of cascading failures based on the self-organizing critical theory and the safety margin of non-faulty circuits.Combining the IEEE-RTS 79 system parameters, the geo-location of each bus is estimated.Taking this system as an example and using Power World simulator, the research results verify that the proposed model can reflect the geomagnetic storm parameters against the power system fault chains and the identification of weak links under given grid conditions.The research results can provide a basis for quantifying and preventing disasters in the magnetic storm condition.
-
Key words:
- geo-magnetic storm /
- fault chain model /
- self-organized critical theory /
- stability margin /
- weak links
-
高功率发射技术是高功率微波系统重要基础之一，随着高功率微波系统向更高功率、更高频率、波束扫描、功率合成，多频复用、多平台共形等技术领域的深入发展，仅以功率容量与发射效率为主要出发点的高功率微波天线设计思路，已不能匹配高功率微波系统能力构建的现实需要。着眼现有高功率天线体制的局限性，国内已开展高功率天线的平面化、阵列化研发工作。其技术优点包括：紧凑、轻便，便于多平台装载应用，高功率容量(传输波导功率容量满足即可)，高口径效率，波束扫描速度快(阵列扫描方式)，系统成本可控，便于多系统空间功率合成。近年来，随着雷达、通信、电子对抗领域应用发展需求的不断提高，促进了天线技术的飞速发展，对于高功率微波发射技术而言，也需要有效借鉴近代天线技术的发展成果，将最新天线技术发展成果应用到高功率微波辐射系统中，构建并研究具备平台适应性强、波束扫描、极化重构、多频复用、共口径、小体积、可共形、可重构的全新体制高功率微波发射系统。本文提出了无移相器自旋转高效平板天线系统，采用辐射栅条自旋转方式实现了空间波束电扫描，在高功率应用下具有以下优点[1-2]：准光学电磁设计原理，非谐振结构，结构鲁棒性高，可采用注塑工艺，重量轻，特别便于高频率、高功率微波加工。相比于传统高功率相控阵天线，具备无移相器结构的空间波束扫描能力，简化了天线机械、电气结构，降低了伺服控制难度及系统成本。相比于传统抛物面天线，低剖面、轻重量更便于系统共形集成，如机载应用时，可与机翼共形; 车载应用时，可与方舱壁共形。
1. 波束形成原理
如图 1所示，无移相器天线采用线性微波源馈电，在平面传输波导中以类TEM波传输[3]。辐射缝隙由天线的辐射栅格等间距组成。类TEM波在平板波导中波速为光速c，因此辐射缝隙间距大小为天线工作中心频率一倍波长。导行波经过辐射缝隙时，耦合微波能量输出，实现微波空间定向辐射。
如图 2所示，无移相器天线采用非谐振栅条结构。通过栅条旋转改变辐射缝隙电场相位分布，实现波束空间扫描。馈电微波在平面传输波导中以类TEM波形式传输，近似按标准TEM波分析。
TEM波相速度是与频率无关的量，为保证其高功率容量，波导工作在真空环境中，平面波导vTEM等于真空中光速c。
如图 2所示，栅条自旋转一定角度时，可从微分角度将缝隙起始距离沿x轴近似分解，则沿x轴辐射缝隙处电场相位分布分解为
{θ1n=2π(d1λ+dλn)θ2n=2π(d2λ+dλn)θ3n=2π(d3λ+dλn)θ4n=2π(d4λ+dλn) (1) 式中：θn为沿y方向辐射缝隙1，2，3，…，n处电场相位; λ为天线工作中心频率波长; d1，d2，d3，d4为缝隙起始距离; d为相邻辐射缝隙间距。
当d等于工作波长λ时，将d4-d3=d3-d2=d2-d1=kdx，其中k=sinβ，为栅条自旋转斜率，β为栅条自旋转角度。代入式(1)，可得x轴相邻dx距离的辐射相位差
Δφ=θ2n−θ1n=θ3n−θ2n=θ4n−θ3n=2πsinβdxλ (2) 由式(2)可得，栅条自旋转时电场沿x轴方向产生相位差，形成波束指向偏转，实现自旋转空间波束扫描。
根据阵列天线辐射原理，其合成电场表达式为
E(θ)=N∑n=1Anei[φn+2π(n−1)sinαdxλ] (3) 式中：An为阵列单元幅度大小; φn为阵列单元相位大小; α为空间方向角; N为单元个数。可得波束指向与阵元相位差关系
Δφ=2πsinαdxλ (4) 式(2)与式(4)均为阵元相位差，由此可得2πsinβdxλ=2πsinαdxλ，即
β=α (5) 波束扫描示意图如图 3所示。由式(5)可得，栅条自旋转角度与波束指向角度相等，栅条未旋转时，波束垂直天线平面0°指向，栅条自旋转角度变大，波束空间扫描指向角度对应变大。
2. 系统组成
如图 4所示，天线系统主要由1分24路功分器网络、自旋转扫描天线、伺服机构、密闭框体组成。1分24路功分器网络将高功率微波源输出模式转换为平板波模式，馈入后端天线。自旋转栅格天线采用栅条非谐振结构，实现平板波模式向空间自由波转换。伺服机构由小功率单电机，高精度角编码器组成，完成自旋转机械结构的驱动。天线、馈电、伺服整体真空密封于框体中，提高系统功率容量。如图 5所示，1分24路功分器网络与自旋转栅格天线按L形装配，便于与高功率微波源一体化集成。
3. 设计仿真
3.1 1分24路功分网络
如图 6所示，1分24路功分网络采用高功率径向线结构[4-6]，将高功率同轴馈电波转换为24路过模矩形TE10模输出，实现向自旋转阵列天线的等幅、同相线性分布馈电形式。仿真得24路功分网络输出幅度在-14.2 dB至-13.5 dB之间，插入损耗理论值小于0.4 dB; 输出相位在-107°至-105°之间，具有较高的相位一致性。仿真电场分布如图 7所示，HFSS软件设置馈电功率大于1 GW，功分网络内场最大值为38.4 MV/m。真空环境下(＜1×10-2 Pa)击穿场强在40 MV/m至60 MV/m之间，该电场数值低于击穿阈值，具有GW量级功率容量。
3.2 自旋转波束扫描天线
如图 8所示，经估算，天线口径面积1200 mm×570 mm，可实现增益36 dB。同时为实现波束±30°扫描，天线纵向尺寸增加到1480 mm[7-8]。因此天线最终尺寸约为1480 mm×580 mm×120 mm。
如图 9、图 10所示，栅条未旋转时，波束0°指向，天线增益为39.5 dB，天线辐射效率60%。栅条30°自旋转时，波束30°指向，天线增益为37.8 dB。扫描增益下降1.7 dB。满足波束±30°扫描要求。
4. 样机测试分析
表 1为天线样机测试结果。从实测结果分析，该阵列天线在300 MHz带宽内，0°指向时增益大于36 dB，如图 11所示，并可现±30°波束扫描，当束±30°指向时，其增益下降损耗小于3 dB。与仿真计算存在的增益差异，主要是由样机加工时，波导表面未做工艺处理，造成微波传输损耗加大，降低天线增益。
表 1 天线测试结果Table 1. Result of testingfrequency rceived power of measured antenna/dBm rceived power of standard antenna/dBm gain of standard antenna/dB gain of measured antenna/dB f-0.15 GHz 23.71 -36.80 23.33 36.42 f -23.32 -36.63 23.39 36.70 f+0.15 GHz -24.56 -37.46 23.48 36.38 5. 结论
本文提出的工作在Ku频段的自旋转波束扫描相控阵天线，无需加载移相馈电网络便可实现相位调节，改变波束指向，具有伺服简单，结构紧凑，平面化、低剖面、轻质的优点。从仿真和实测结果来分析，该阵列天线均具有良好的扫描特性，高口径辐射效率，自旋转扫描范围达到±30°，可广泛应用于机载、车载、舰载高功率微波系统的表面共形发射。
-
图 3 计及地磁暴影响的电力系统事故链仿真模型
Figure 3. Power system fault chain simulation model considering the impact of geomagnetic storm
表 1 IEEE-RTS79系统各母线的地理位置
Table 1. Estimated geo-location of IEEE-RTS79
No. latitude/(°) longitude/(°) No. latitude/(°) longitude /(°) 1 45.276 7 113.770 5 13 45.742 8 114.732 7 2 45.319 9 113.765 8 14 45.390 7 115.061 5 3 45.005 7 114.560 6 15 45.174 2 115.180 3 4 45.094 7 114.188 9 16 45.224 9 115.450 2 5 45.320 4 114.133 9 17 45.192 9 115.133 6 6 45.553 7 114.507 8 18 45.199 2 115.397 0 7 45.451 7 113.608 0 19 45.398 1 115.235 7 8 45.329 6 113.810 7 20 45.75 9 115.405 0 9 45.366 3 114.526 0 21 45.415 9 115.680 5 10 45.366 3 114.526 0 22 46.022 5 115.833 5 11 45.366 3 114.526 0 23 45.932 2 115.590 0 12 45.366 3 114.526 0 24 45.005 7 114.360 6 
下载: 导出CSV
表 2 初始故障的设定
Table 2. Initial failure setting
geomagnetic data SOC lines γi E=0 L10(B6-10)
L25(B15-21)
L23(B14-16)1.547 0
1.361 6
1.165 9E=12 V/km，130° L10(B6-10)
L25(B15-21)
L23(B14-16)1.496 1
1.347 1
1.153 4E=12 V/km，46° L10(B6-10)
L25(B15-21)
L7(B3-24，T)
L23(B14-16)1.480 7
1.340 2
1.193 3
1.152 1
下载: 导出CSV
表 3 不同磁暴条件下系统的事故链集
Table 3. Fault chain sets
geomagnetic data No. fault chains E=0 1 L10-L5-L25-L29 2 L25-L23-L30-L28-L34-L37 3 L23-L29 E=12 V/km，130° 4 L10-L5-L25-L29 5 L10-L5-L25-L30-L33-L28-L34 6 L25-L23-L30-L28-L34-L37 7 L23-L29 8 L23-L7(T) E=12 V/km，46° 9 L10-L5-L25-L29 10 L10-L5-L25-L30-L33-L28 11 L25-L28-L30-L28-L34 12 L7(T)- L23 13 L7(T)-L6-L2-L28-L23 14 L7(T)-L28-L24-L25-L33-L34 15 L23-L29
下载: 导出CSV
表 4 事故链13的生成过程
Table 4. Process of fault chain 13
fault line non-faulty line si L7(B3-24，T) L6(B3-9) 1.1102 L6(B3-9) L2(B1-3) 1.0328 L2(B1-3) L28(B14-16) 1.0293 L28(B14-16) L23(B14-16) 1.0565 L23(B14-16) blackout —
下载: 导出CSV
-
[1] 刘文颖, 杨楠, 张建立, 等. 计及恶劣天气因素的复杂电网连锁故障事故链模型[J]. 中国电机工程学报, 2012, 32(7): 53-59. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201207008.htmLiu Wen-ying, Yang Nan, Zhang Jianli, et al. Complex grid failure propagating chain model in consideration of adverse weather. Proceedings of the CSEE, 2012, 32(7): 53-59 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201207008.htm [2] 刘连光, 吴伟丽. 磁暴影响电力系统安全风险评估思路与理论框架[J]. 中国电机工程学报, 2014, 34(10): 1583-1591. doi: 10.13334/j.0258-8013.pcsee.2014.10.009Liu Lianguang, Wu Weili. Security risk assessment ideas and theoretical framework for power system considering geomagnetic storm. Proceedings of the CSEE, 2014, 34(10): 1583-1591 doi: 10.13334/j.0258-8013.pcsee.2014.10.009 [3] Boteler D H. Geomagnetic hazards to conducting networks[J]. Natural Hazards, 2003, 28(2-3): 537-561. [4] 罗毅, 王英英, 万卫, 等. 电网连锁故障的事故链模型[J]. 电力系统自动化, 2009, 33(24): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT200924002.htmLuo Yi, Wang Yingying, Wan Wei, et. al. Fault chains model for cascading failure of grid. Automation of Electric Power Systems, 2009, 33(24): 1-5 https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT200924002.htm [5] 顾雪平, 刘雨濛, 王涛, 等. 基于结构平衡理论的电网自组织临界态辨识[J]. 电工技术学报, 2018, 33(17): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201817022.htmGu Xueping, Liu Yumeng, Wang Tao, et al. Self-organized critical state identification of power systems based on structural equilibrium theory. Transactions of China Electrotechnical Society, 2018, 33(17): 1-10 https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201817022.htm [6] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Trans Magnetics, 2010, 46(4): 1100-1115. doi: 10.1109/TMAG.2009.2038153 [7] 何飞, 梅生伟, 薛安成, 等. 基于直流潮流的电力系统停电分布及自组织临界性分析[J]. 电网技术, 2006, 30(14): 7-12. doi: 10.3321/j.issn:1000-3673.2006.14.002He Fei, Mei Shengwei, Xue Ancheng, et al. Blackout distribution and self-organized criticality of power system based on DC power flow. Power System Technology, 2006, 30(14): 7-12 doi: 10.3321/j.issn:1000-3673.2006.14.002 [8] 岳贤龙, 王涛, 顾雪平, 等. 基于自组织临界理论的电网脆弱线路辨识[J]. 电力系统保护与控制, 2016, 44(15): 18-26. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201615003.htmYue Xianlong, Wang Tao, Gu Xueping, et al. Vulnerable line identification of power grid based on self-organizing critical theory. Power System Protection and Control, 2016, 44(15): 18-26 https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201615003.htm [9] Overbye T J, Hutchins T R, Shetye K, et al. Integration of geomagnetic disturbance modeling into the power flow: A methodology for large-scale system studies[C]//IEEE North American Power Symposium. 2012: 1-7. [10] 于群, 郭剑波. 我国电力系统停电事故自组织临界性的研究[J]. 电网技术, 2006, 30(6): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200606001.htmYu Qun, Guo Jianbo. Study on self-organized criticality of power system blackouts in China. Power System Technology, 2006, 30(6): 1-5 https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200606001.htm [11] Carreras B A, Lynch V E, Dobson I, et al. Dynamics, criticality and self-organization in a model for blackouts in power transmission systems[C]//IEEE Hawaii International Conference on System Sciences. 2002, 9: 1-9. [12] 吴伟丽. 磁暴诱发电网故障灾害风险分析研究进展[J]. 科学技术与工程, 2016, 16(9): 135-141. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201609022.htmWu Weili. Review of risk analysis for severe grid accident due to geomagnetic storm. Science Technology and Engineering, 2016, 16(9): 135-141 https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201609022.htm [13] 王英英. 基于事故链的电力系统连锁故障风险评估与预防控制研究[D]. 武汉: 华中科技大学, 2010.Wang YingYing. Risk assessment and prevention control of cascading failures in power system based on fault chains. Wuhan: Huazhong University of Science & Technology, 2010 [14] 宋毅, 王成山. 一种电力系统连锁故障的概率风险评估方法[J]. 中国电机工程学报, 2009, 29(4): 27-33. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200904006.htmSong Yi, Wang Chengshan. A probabilistic risk assessment method for cascading failure of power system. Proceedings of the CSEE, 2009, 29(4): 27-33 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200904006.htm [15] 刘友波, 胥威汀, 丁理杰, 等. 电力系统连锁故障分析理论与应用(二): 关键特征与研究启示[J]. 电力系统保护与控制, 2013, 41(10): 146-155. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201310027.htmLiu Youbo, Xu Weiting, Ding Lijie, et al. Power system cascading failure analysis theories and application Ⅱ: Key features of real cascading failures and revelation aspects. Power System Protection and Control, 2013, 41(10): 146-155 https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201310027.htm [16] Dobson I, Chen J, Thorp J S, et al. Examining criticality of blackouts in power system models with cascading events[C]//IEEE Hawaii International Conference on System Sciences. 2002, 10: 1-10. 期刊类型引用(1)
1. 秦洪才，袁成卫，宁辉，孙云飞，张强，许亮，严鹏. 高功率平板波导螺旋阵列天线设计. 强激光与粒子束. 2021(02): 52-56 . 
本站查看其他类型引用(6)
-
下载:
点击查看大图
计量
- 文章访问数: 1521
- HTML全文浏览量: 484
- PDF下载量: 74
- 被引次数: 7
