Smoothing of mid-spatial frequency errors by computer controlled surface processing
-
摘要: 数控抛光已被广泛应用于光学元器件的加工制造，而抑制元件表面中频误差是加工过程中一项十分重要的内容。基于Presston方程对数控小工具抛光盘去除函数进行了建模，得到了理论化的去除函数表达式。结合去除函数，在参数化匀滑模型基础上通过建立多参数的时变理论模型，表明元件表面中频误差是随抛光过程呈指数型收敛的，其收敛效率取决于材料参数、体积去除率等抛光工艺参数。对理论模型的匀滑曲线进行了模拟分析，实现了不同工艺条件下的匀滑效率的对比。结果表明：在不同抛光盘材料的匀滑过程中，材料系数越大，其整体匀滑效率越高。同样，抛光盘体积去除率越大，对表面误差的匀滑效率也会越高。进行了一组空间周期分别为3，5，7 mm的波纹误差的匀滑实验，其结果表明，在相同的抛光参数下，具有较大空间频率的波纹匀滑效率会更高，收敛曲线下降得更快。最后对比了不同材料抛光盘匀滑效率，从实验上证实了沥青盘在波纹匀滑效率上远高于聚氨酯材料的抛光盘。Abstract: Computer Controlled Surface Processing(CCOS) technology has been widely and successfully applied to the manufacture of optical components. In typical extreme optical manufacturing engineering, smoothing the surface errors is a very important process. Based on Presston equation, the tool influence function (TIF) of polishing pad is modeled, and the theoretical expression of TIF is obtained. Based on the parametric smoothing model, a multi-parameter time-dependent theoretical model is established. The results show that the surface error of components converges exponentially with the polishing process, and the convergence efficiency depends on the polishing parameters such as material parameters and volume removal rate. The smoothing curve of the theoretical model is simulated and analyzed, and the smoothing efficiency under different technological conditions is compared. The results show that the higher the material coefficient is, the higher the overall smoothing efficiency is. Similarly, the larger the volume removal rate of the polishing pad, the higher the smoothing efficiency of the surface error. A series of smoothing experiments with 3, 5 and 7 mm ripple errors were carried out. The results show that under the same polishing parameters, the smoothing efficiency of ripple with larger spatial frequency will be higher and the convergence curve will decline faster. Finally, the smoothing efficiencies of different material are compared, and the experimental results show that the smoothing efficiency of pitch pad is much higher than that of polyurethane polishing pad.
-
Key words:
- CCOS /
- tool influence function /
- smoothing model /
- material parameters /
- spatial frequency
-
为满足现代天文学、军事等领域对大口径、高精度的光学元件的需求，计算机控制表面成型技术(CCOS) 在精密光学元件加工上得到了广泛的应用与发展[1-3]。从小尺寸的光学镜片到大型天文望远镜，抑或高功率的激光系统，CCOS都为其光学器件的制造提供了确定性的材料去除技术[4]。目前对光学元件常用的加工方法主要包括：磁流变抛光、气囊抛光、数控小工具抛光以及离子束抛光、高频振动抛光等不同的加工方式[5-8]。而数控抛光从20世纪70年代开始兴起并在光学加工应用中发展得较为成熟[9]，其特点是利用一个尺寸比加工工件小得多的抛光工具，在计算机控制下以一定的路线、速度和压力在工件表面进行材料去除，从而得到比传统加工方法精度更高的加工结果。
在极端光学系统中，其元器件的表面误差是影响整个系统成像和运行质量的极为关键的因素。光学元件表面误差按空间频率主要分为低频误差、中频误差和高频误差三类。低频误差能使光学元件产生像差，导致光学系统成像扭曲；中频误差能造成光线的小角度散射，进而影响系统成像的对比度；而高频误差的存在能使光线发生大角度散射，从而使得光学元件的镜面反射率明显降低[10]。其中，对抑制中频误差的理论和工艺方法最为困难。因此，在生产制造和工艺流程中，对光学元件表面中频误差的形成机理、抑制方法等方面进行深入研究具有十分重要的意义。
近年来，关于中频误差的匀滑已有大量的研究工作及成果。Mehta和Reid最早提出柔性盘，并基于弹性理论建立了桥模型[11-12]。桥模型描述半柔性工具的匀滑效果，当抛光工具在工件上移动时，抛光盘接触面会不断地随局部曲率产生弯曲，导致压力分布的连续变化。桥模型给出了柔性抛光盘在匀滑波纹误差时的压力理论方程，解释了抛光盘对光学元件表面波纹误差的匀滑原理，并通过理论方程给出了正弦波纹的压力分布。桥模型首次提出了波纹匀滑理论，而实际上，光学元件表面波纹通常是形状随机，并不一定满足正弦形分布，因此通过有限元方法对无规律形状波纹的压力分析更为精确[13]。Kim对RC盘做了大量研究工作，并且基于桥模型提出了参数化的匀滑数学模型[14]来描述各种抛光工艺的抛光效果及效率[15]，参数化匀滑模型通过对元件表面中频误差的连续匀滑实验数据进行线性拟合，通过拟合直线斜率来对比不同抛光参数的匀滑效率。然而，参数化匀滑模型给出了平均匀滑因子(S)与波纹幅值(ε)的关系，但忽略了时变特性，于是基于参数化模型在抛光过程中通过考虑匀滑时间揭示了表面误差的演变，得到了指数型下降的函数图像[16]。
本文针对数控抛光中的沥青盘小工具对元件表面误差的自匀滑机理进行研究工作。在现有的理论模型基础上结合去除函数表达式，给出了一个包含各项工艺参数的匀滑演化模型。接下来，通过一组不同周期表面波纹误差的匀滑实验，探究了元件表面误差的空间频率对于匀滑效率的影响关系。同时，通过对比不同抛光垫材料的匀滑效果，证实了高弹性模量的沥青盘比聚氨酯盘在相同的抛光工艺参数下具有更好的自匀滑效果。
1. 理论模型
1.1 小工具数控抛光的去除函数
数控抛光中，去除函数(TIF)定义为单位时间内的材料去除量。其大小和分布受不同的抛光方式和抛光参数影响。从理论上讲，抛光过程实际就是去除函数在工件上移动后去除量的叠加过程。一般来说，去除函数模型的建立是基于经典的Preston方程[1]
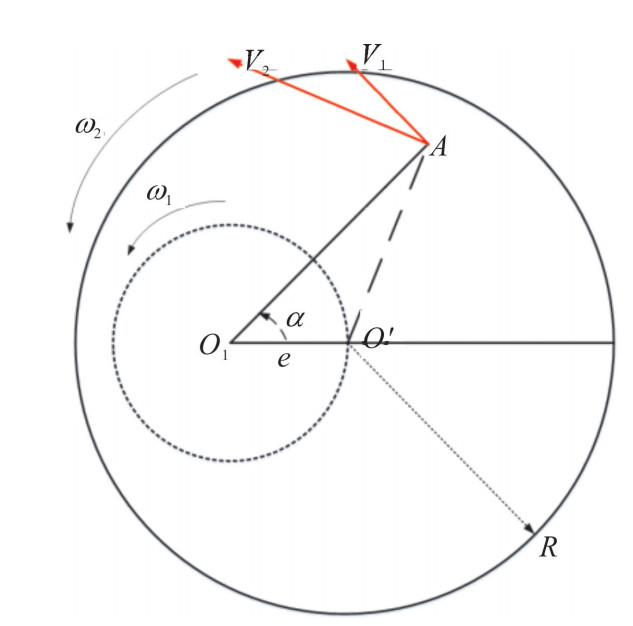
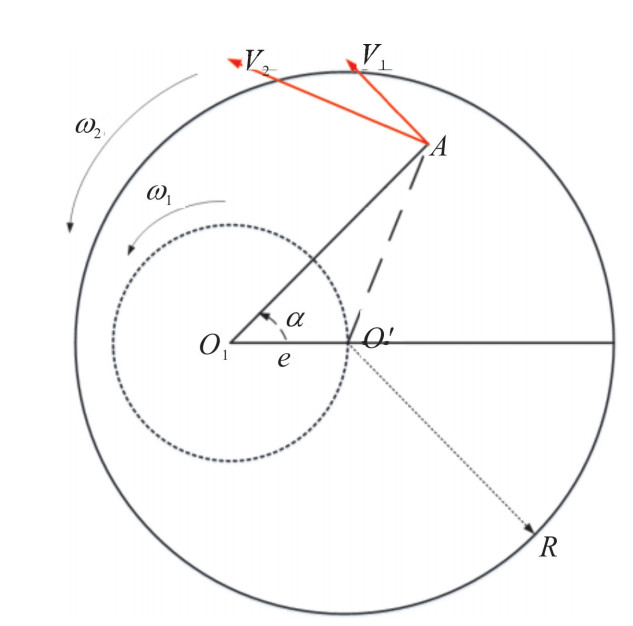
dz=KPv (1) 式中: dz为材料去除量; K是一个与抛光环境相关的参数，其受抛光过程中的化学、温度、抛光粉等因素的影响; v为抛光盘与工件的相对速度; P是抛光盘与工件之间的压强。在小工具数控抛光过程中，抛光盘在转轴下以双行星运动方式工作，如图 1所示。图中: A为元件上某一点; 抛光盘公转中心为O1, 自转中心即抛光盘中心为O′, O1与O′间距为e，即偏心距; A点到O1的距离为r; R为抛光盘半径; v1, v2分别为A点的公转线速度和自转线速度; O1, A和O′夹角为α。
考虑Preston方程中系数K为常数以及压强P均匀分布时，由于抛光盘运动方式引起的相对速度v不同，该参数分布下的去除函数表达式为
F(r)=KPω12π∫θ−θ√r2(1+n)+e2n2−2ren(1+n)cosαdα (2) 其中
n=ω2ω1 (3) 积分区间θ满足如下条件
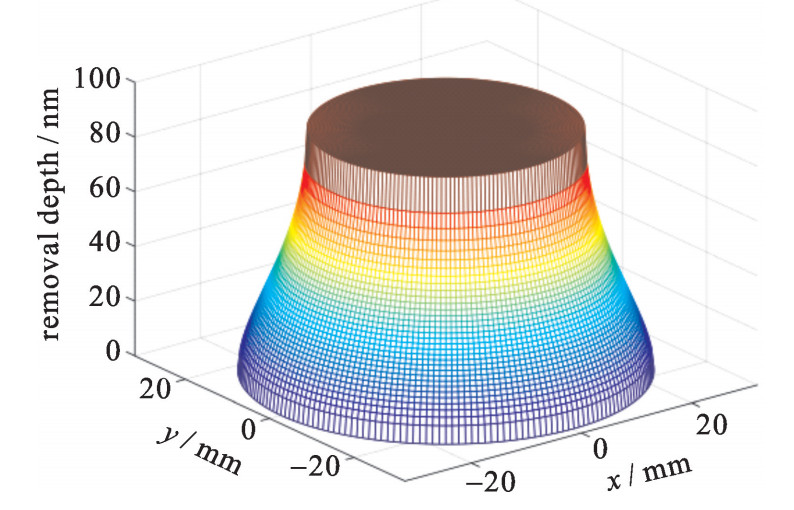
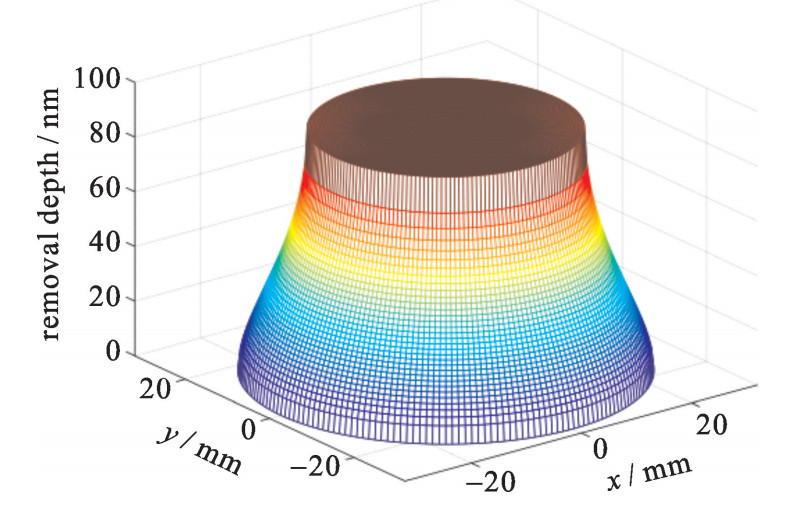
θ={2π,r⩽ (4) 图 2给出了一个典型的去除函数分布形貌，其中，参数K以及压强P设为1。可见在抛光盘的驻留范围内，抛光过程对元件表面的材料去除一般来说是非均匀的。通过去除函数特征分析，能得出表示单位时间内总的材料体积去除率(RVRR)，以及表示去除函数最大值的峰值去除率(RPRR)。其对应的表达式为(其中积分区间S为去除函数的范围)
R_{\mathrm{VRR}}=\iint_S F(x, y) \mathrm{d} x \mathrm{~d} y (5) R_{\mathrm{PRR}}=\max (F) (6) 
图 2 抛光盘半径25 mm，偏心距5 mm，公转160 r/min，自转8 r/min参数下理论去除函数Figure 2. Theoretical TIF under the parameters of radius 25 mm, eccentricity 5 mm, revolution 160 r/min and rotation 8 r/min1.2 小工具数控抛光对元件表面中频误差的匀滑理论模型
在数控抛光对光学元件表面误差的匀滑研究过程中，建立一个合理有效的数学模型是非常重要的。对于粘弹性小工具的匀滑效果已经有了一定的研究成果。从桥模型到参数化模型的建立，都为数控抛光的匀滑作用提供了有力的理论指导。
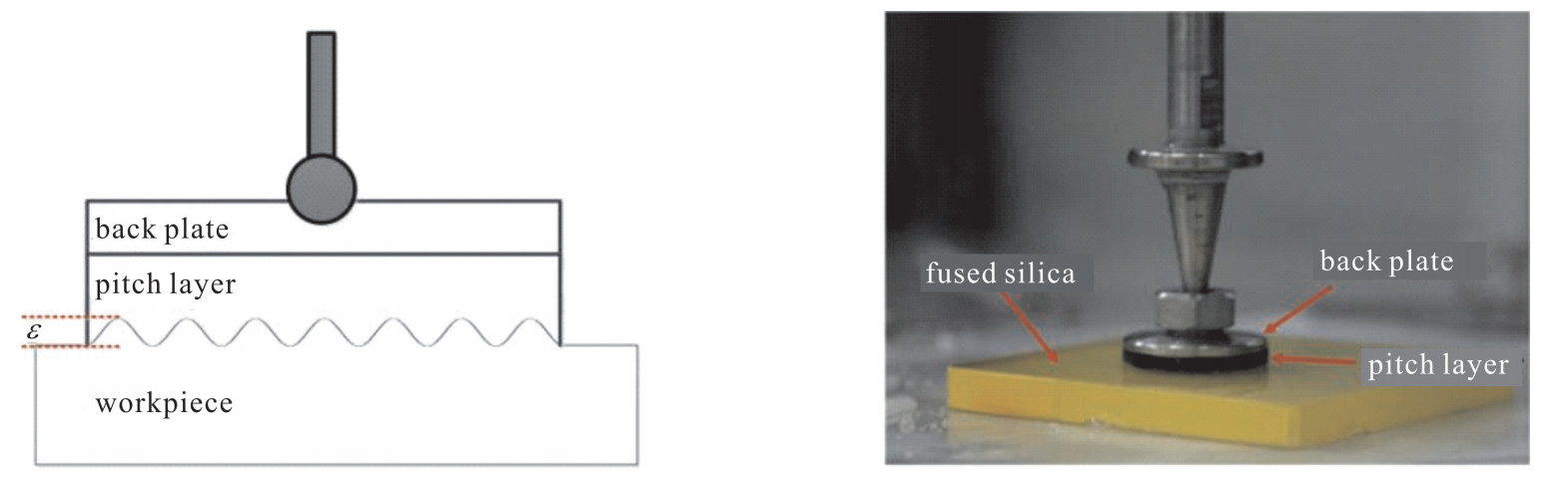
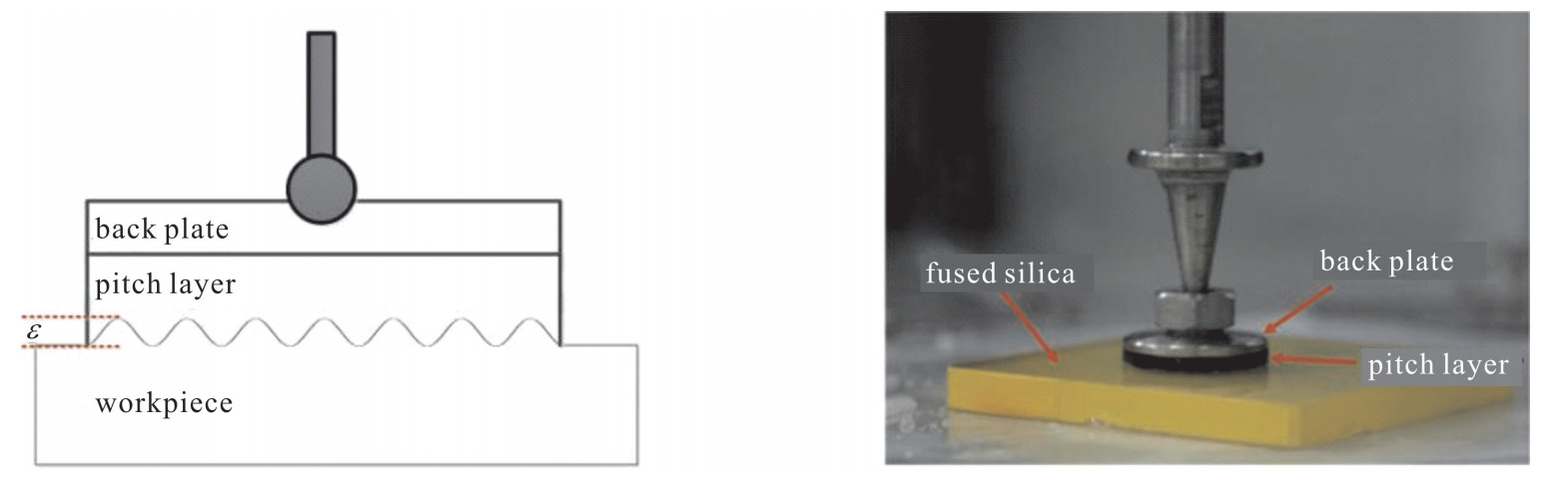
如图 3所示，波纹误差导致沥青抛光盘与工件表面接触不均匀，从而产生局部压力分布的不均匀。对于半柔性抛光盘在具有波纹误差的元件表面的接触压力分布，桥模型理论给出了如下方程，即[14]
P(x)=P_{\text {nominal }}+\frac{\varepsilon(x)}{\frac{1}{D_{\text {plate }}(2 {{\rm{ \mathsf{ π} }}} \xi)^4}+\frac{1}{D_{\text {s_plate }}(2 {{\rm{ \mathsf{ π} }}} \xi)^2}+\frac{1}{\kappa_{\text {total }}}} (7) 
图 3 抛光盘在具有波纹误差的工件表面接触示意图以及实际抛光平台Figure 3. A pitch polishing pad contact on the workpiece with ripple error and the experiment platform该模型中，ε为表面波纹误差，ξ为空间频率。考虑一维情况，故取元件表面x轴为空间变量。抛光盘为柔性层附夹一层薄金属盘的结构。Pnominal为波纹谷值处的压强，Dplate为薄金属层抗弯刚度，Ds_plate为其横向剪切刚度，κtotal为抛光盘整体材料刚度系数。而对于数控抛光沥青盘，由于不需要附夹一层薄金属盘，故其接触压强分布可表示为
P(x)=P_{\text {nominal }}+\kappa_{\text {total }} \varepsilon(x) (8) 可以看出，在具有波纹误差的元件表面上，抛光过程中，接触压强随波纹误差幅值发生变化，在波纹峰值处会比波纹谷值多出一个压强差，记为Padd。由Presston方程可知，抛光过程中材料去除量是正比于抛光压强的，因此，波纹峰值处材料去除量会更大，从结果上来看，工件会变得更平滑，从而达到表面波纹的匀滑效果。根据Presston方程容易得知，工件表面波纹的材料去除满足
\Delta \varepsilon=K P_{\text {add }} v \Delta t (9) 式中: K为常参数，Padd为波纹处与误差谷值处压强差。对于粘弹性特性的抛光盘(如沥青盘，RC盘等)，Kim建立了参数化匀滑模型[14]
S=\frac{\Delta \varepsilon}{\Delta Z}=k\left(\varepsilon_{\text {ini }}-\varepsilon_0\right) (10) 式中：S为匀滑因子，定义匀滑因子S为波纹去除量与材料去除深度之比，其大小表征了抛光过程中对波纹误差的匀滑能力; Δε为波纹去除深度; ΔZ为总材料去除深度; ε0为工件表面最终波纹深度，即为匀滑作用的极限; εini为每次抛光过程的初始表面波纹幅值。可以看出，数控抛光的匀滑因子S与工件表面波纹幅值ε呈线性关系，比例系数为k。在参数化匀滑模型中
k=\frac{\kappa_{\text {total }}}{P} (11) \frac{1}{\kappa_{\text {total }}}=\frac{1}{\kappa_{\text {elastic }}}+\frac{1}{C} (12) 式中：P为抛光盘压强，κtotal代表整体的抛光盘材料系数，其与柔性层弹性材料系数κelastic和抛光盘其他结构的材料系数以及斜率修正因子C有关，该模型中，常数C是用以修正实际加工数据与模型表达式的拟合参数。参数化匀滑模型揭示了匀滑因子，即匀滑效率与表面波纹误差幅值的线性关系，斜率k越大，代表对相同表面误差的匀滑效率越高。
利用参数化匀滑模型中的匀滑因子的数学表达式，可得到
\frac{\mathrm{d} \varepsilon}{\mathrm{d} Z}=\frac{\mathrm{d}\left(\varepsilon-\varepsilon_0\right)}{\mathrm{d} Z}=-k\left(\varepsilon-\varepsilon_0\right) (13) 则
\varepsilon=\left(\varepsilon_{\text {ini }}-\varepsilon_0\right) \mathrm{e}^{-k Z}+\varepsilon_0 (14) 去除深度Z可以表示为抛光盘的平均材料去除率与时间的乘积，即
Z=\frac{R_{\mathrm{VRR}}}{{{\rm{ \mathsf{ π} }}} R_{\mathrm{F}}^2} t (15) 式中: RF为去除函数半径。因此，最终多参数匀滑演化模型可表示为
\varepsilon=\left(\varepsilon_{\text {ini }}-\varepsilon_0\right) \exp \left(-\kappa_{\text {total }} \frac{R_{\mathrm{VRR}}}{P {{\rm{ \mathsf{ π} }}} R_{\mathrm{F}}^2} t\right)+\varepsilon_0 (16) 可以看出，抛光过程中，元件表面中频误差是随时间呈指数型收敛的。其收敛速度即元件表面误差的匀滑效率是与抛光盘材料、材料的体积去除率、抛光压强以及抛光盘尺寸等诸多工艺参数直接相关的。
2. 匀滑模拟及实验
2.1 理论匀滑曲线的模拟
通过匀滑模型方程，便能够从理论上探究不同的抛光工艺参数对整个匀滑效率的影响。虽然理论计算各项表达式因子与实际会有一定差异，但是整个变化趋势是与实际相符的。
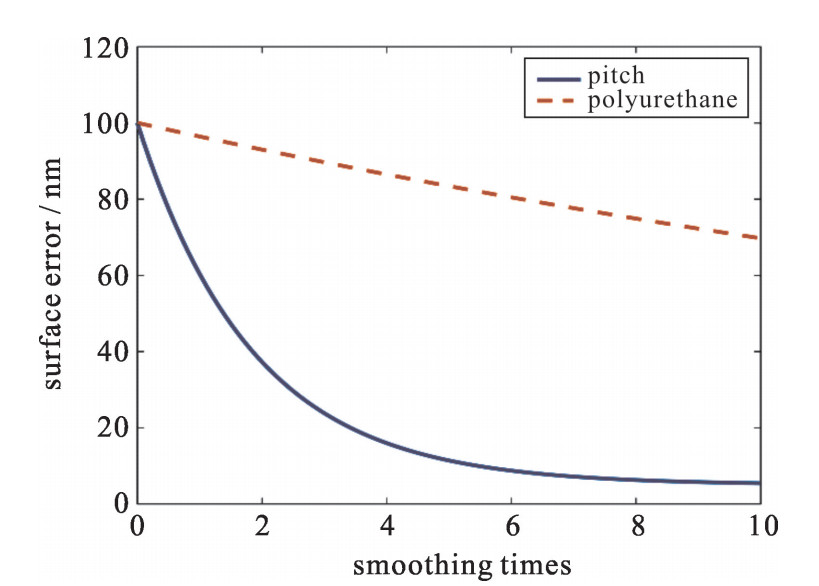
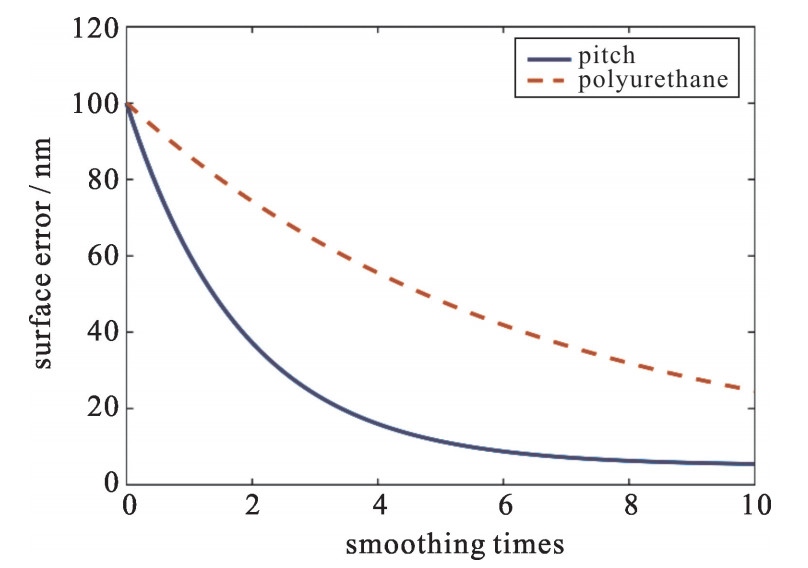
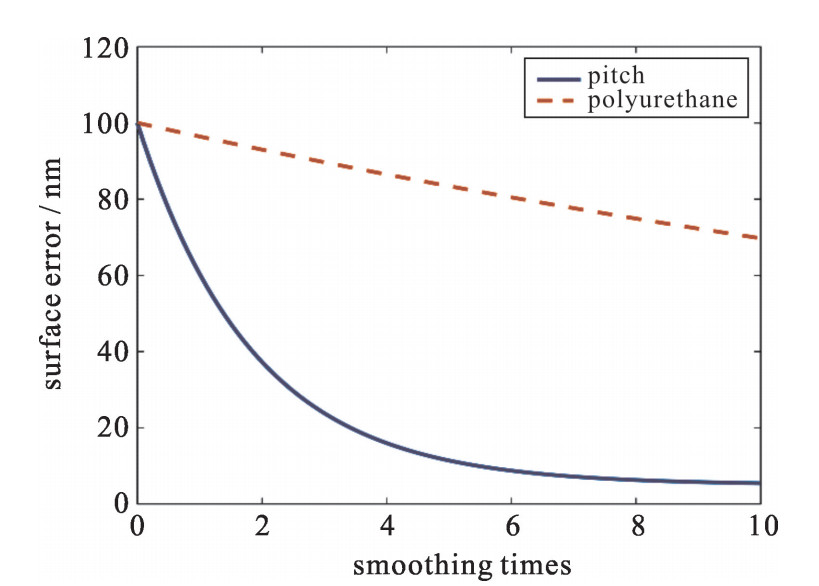
首先模拟不同抛光盘材料对于匀滑效率的影响。由于不同材料的弹性系数κelastic不相同，从而必将导致其整体材料系数存在差异，这样便产生了不同材料的抛光盘在相同工艺环境下对光学元件的匀滑效率不同的现象。常见的抛光盘材料主要有沥青和聚氨酯，一般来说，前者的弹性系数是远大于后者的(沥青弹性模量Epitch≈6.75×108, 聚氨酯弹性模量Epolyurethane≈4.8×107)。设定其他工艺参数相同的情况下，从理论上能计算出沥青抛光盘与聚氨酯抛光盘对具有初始波纹深度100 nm的元件匀滑效果对比如图 4所示。
图 4 沥青抛光盘与聚氨酯抛光盘匀滑过程理论曲线对比Figure 4. Theoretical smoothing curves of pitch pad and polyurethane pad从理论模拟图中能看出，由于沥青的弹性系数大于聚氨酯材料，从而导致沥青盘对元件波纹误差的匀滑效率远高于聚氨酯盘。
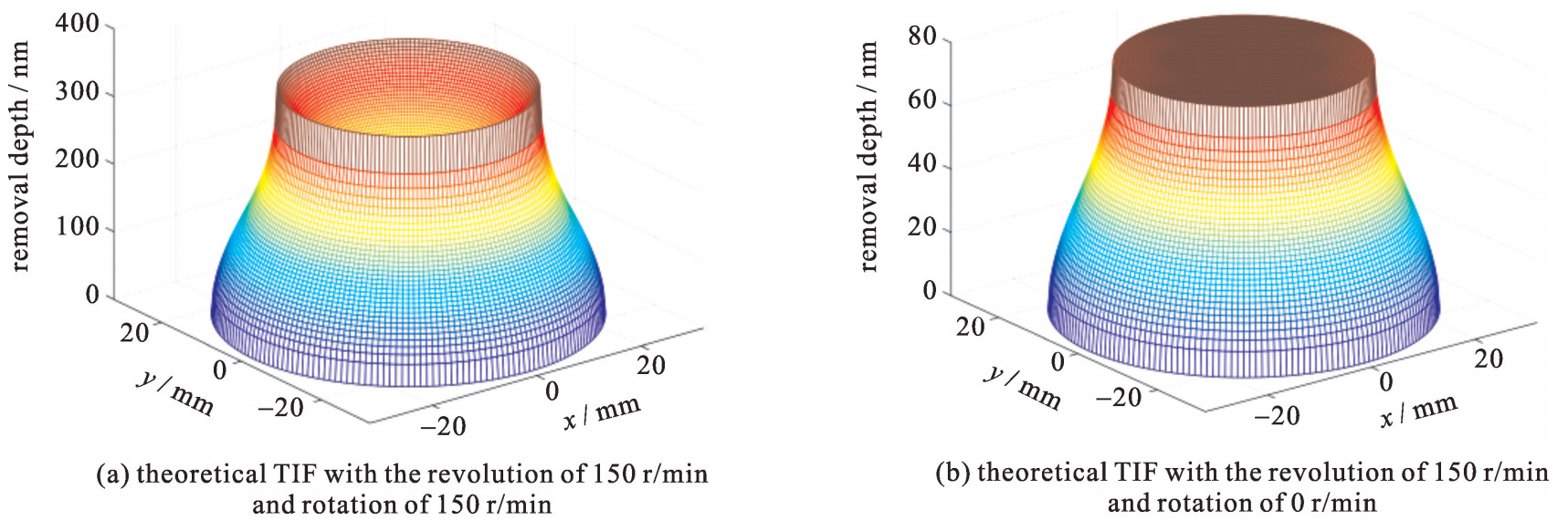
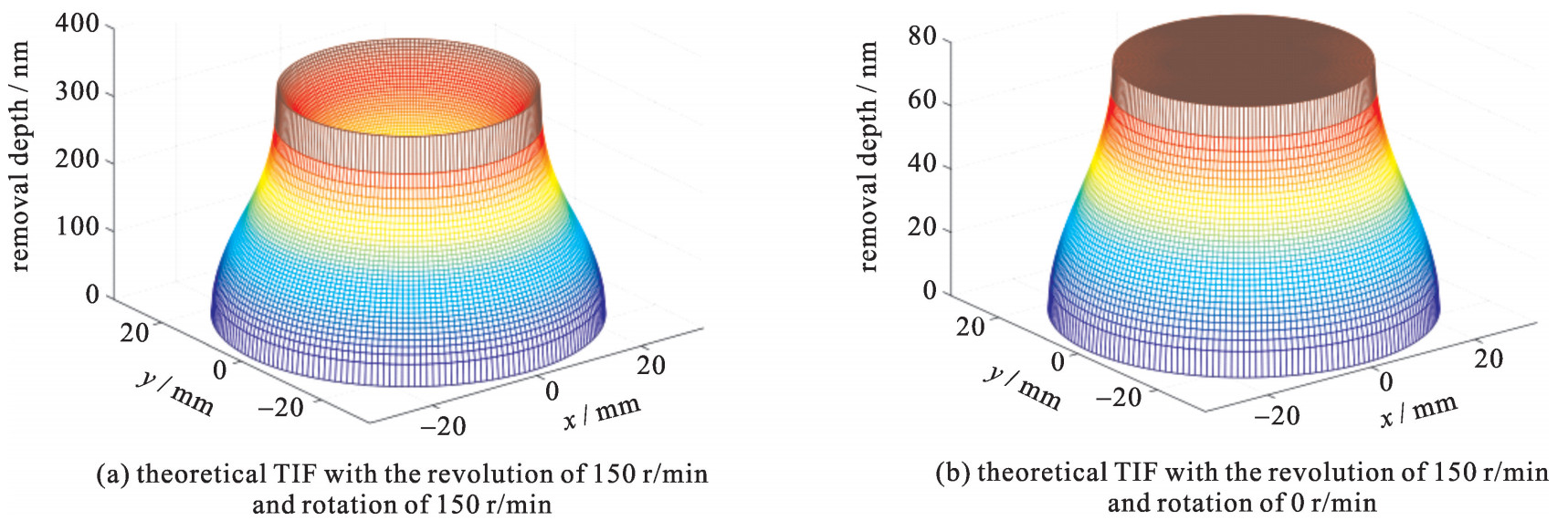
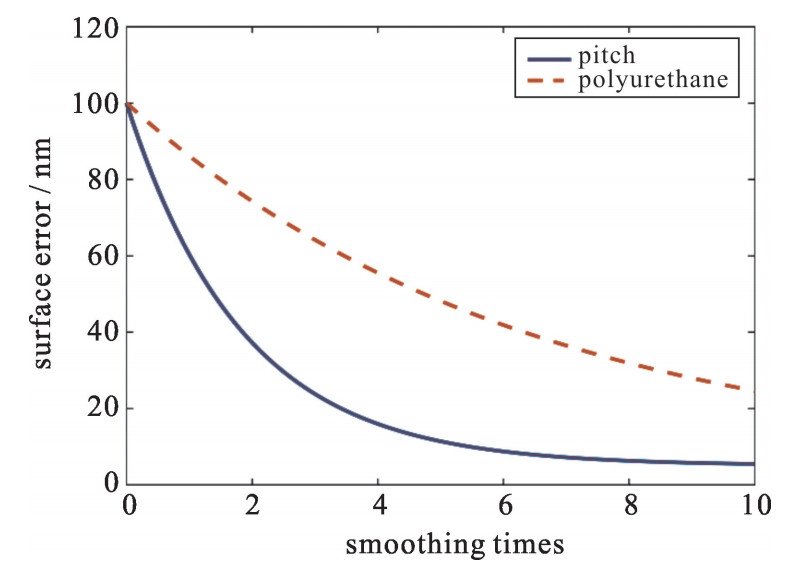
探究了材料对匀滑作用的影响后，接下来将对不同工艺参数下的匀滑效果进行理论仿真。根据方程(16)可知，工艺参数包含了材料体积去除率RVRR，抛光压强P等。而不同抛光盘转动情况下的去除函数是不相同的，因而其体积去除率存在差异，因此，容易通过改变抛光盘转动参数而调节体积去除率，从而探究不同体去除率下的匀滑效率。模拟选用半径25 mm，偏心距5 mm的抛光盘。第一组公自转为ω1=150 r/min, ω2=-150 r/min；第二组公自转为ω1=150 r/min, ω2=0 r/min。理论去除函数以及匀滑曲线对比如图 5~6所示。
图 5 不同抛光盘转动参数下理论去除函数对比Figure 5. Comparison of theoretical TIF of different rotation parameters
图 6 不同抛光盘转动参数匀滑过程理论曲线对比Figure 6. Comparison of theoretical smoothing curves of different rotation parameters从理论模拟图中可知，相同的抛光盘在只做公转运动情况下的匀滑效率是低于双行星运动情况的，因为在公转相同的情况下，具有自转的抛光方式其体积去除率RVRR, 1比无自转时的体积去除率RVRR, 2相对更高(RVRR, 1/RVRR, 2≈3.4)，导致其匀滑效率更高。
2.2 不同空间周期波纹的匀滑实验
为了探究匀滑效率与波纹空间频率的关系，进行了一组匀滑实验对比。本次实验对象为三块100 mm×100 mm的熔石英元件，其表面分别具有空间间隔为3, 5, 7 mm的初始波纹误差。将这三块熔石英元件在同一数控抛光平台上进行连续匀滑抛光实验。
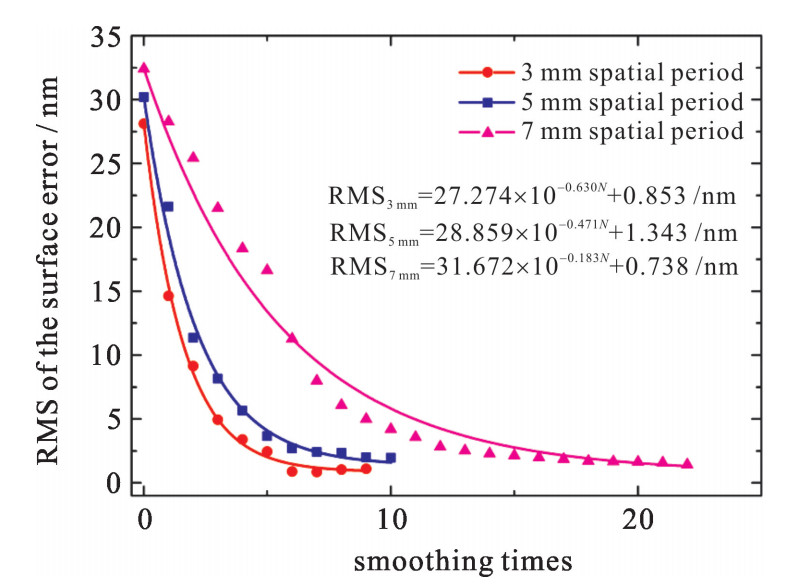
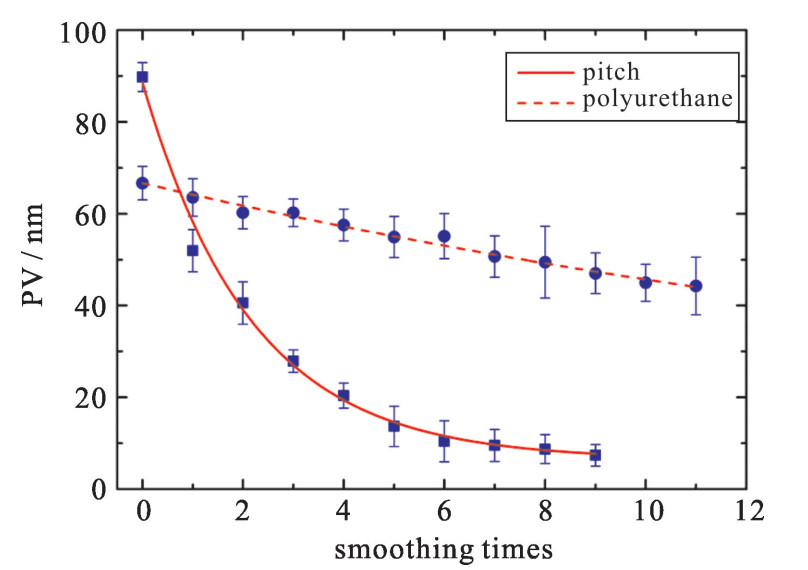
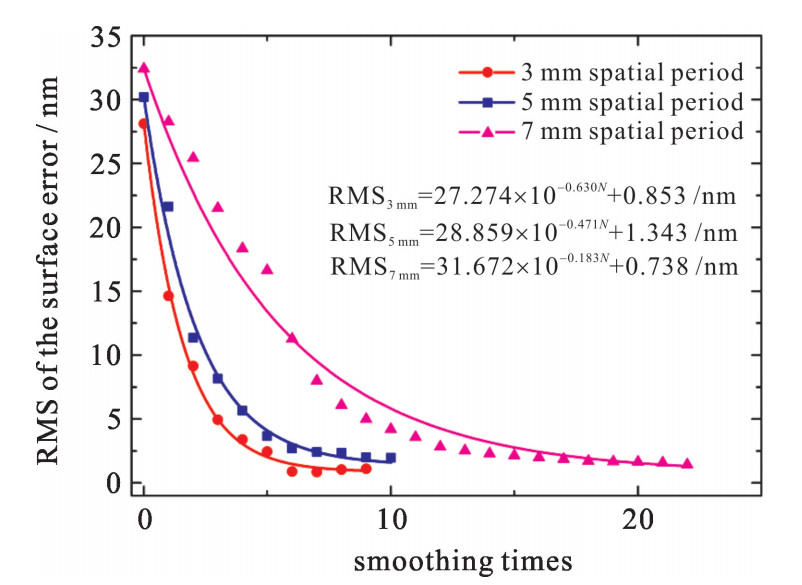
实验采用直径35 mm沥青盘进行抛光，偏心距设定为3 mm，公转200 r/min，自转20 r/min，且自转方向与公转方向相反。在元件表面上，抛光头以光栅路径行进，进给速度设定为200 mm/min，光栅间距为3 mm。在初始时刻以及每完成一次抛光后都会对三块熔石英元件进行面型检测。针对每一个熔石英元件，当实验进行到元件表面波纹误差变化不明显的时候，即达到匀滑极限时便停止该组实验的抛光工作。三组元件的表面误差随抛光次数的变化曲线如图 7所示。
图 7 不同空间周期波纹误差匀滑实验数据拟合曲线Figure 7. Data points and the fitting curves of the three workpieces with different spatial-period ripple error in the smoothing experiment通过实验发现，波纹误差空间间隔为3 mm的元件从初始到抛光到匀滑极限的实验次数最少，而波纹误差空间间隔为7 mm的元件所用实验次数最多，说明其匀滑过程相对更为缓慢，匀滑效率相对较低。三组实验中，除了工件的初始表面波纹误差空间频率外，抛光过程的各项工艺参数都是相同的，根据Kim在参数化匀滑模型中的研究，波纹频率会影响到沥青层弹性系数κelastic。对比三组实验的匀滑结果，表明波纹空间频率越高，则材料因子κtotol越大，从而匀滑效率更高，匀滑实验收敛曲线下降越快。
2.3 不同抛光盘材料的匀滑实验
前面进行的实验是利用沥青作为抛光盘材料的，接下来通过控制变量，在工艺参数基本相同的情况下，进行一组以沥青和聚氨酯为抛光盘材料的匀滑对比实验。实验选取两块直径150 mm圆形熔石英元件，元件表面具有空间间隔为5 mm，深度70 nm左右的初始波纹误差。沥青和聚氨酯抛光盘直径都为50 mm，偏心距5 mm。在同一数控抛光机床上进行加工，且抛光程序设定一致。
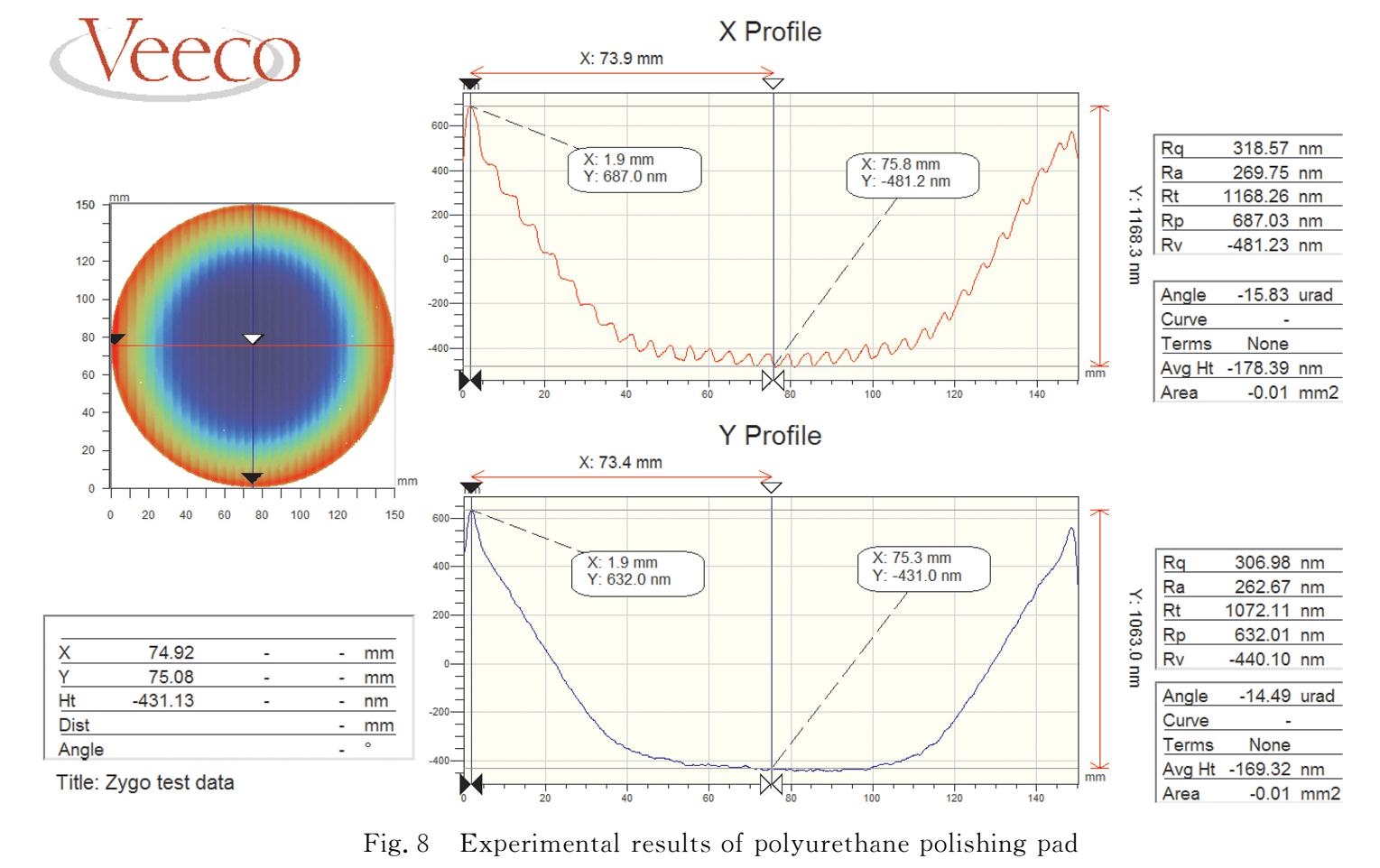
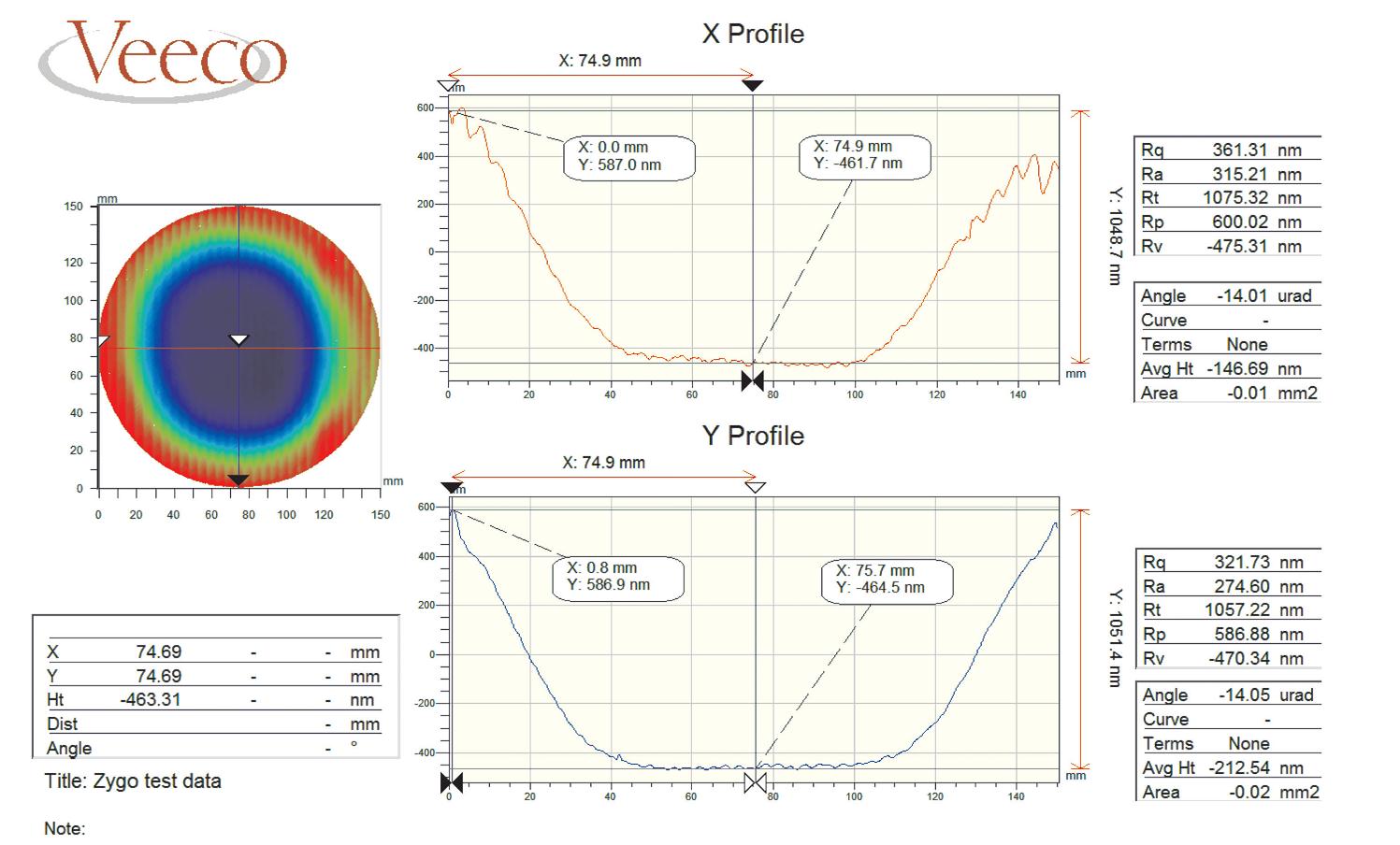
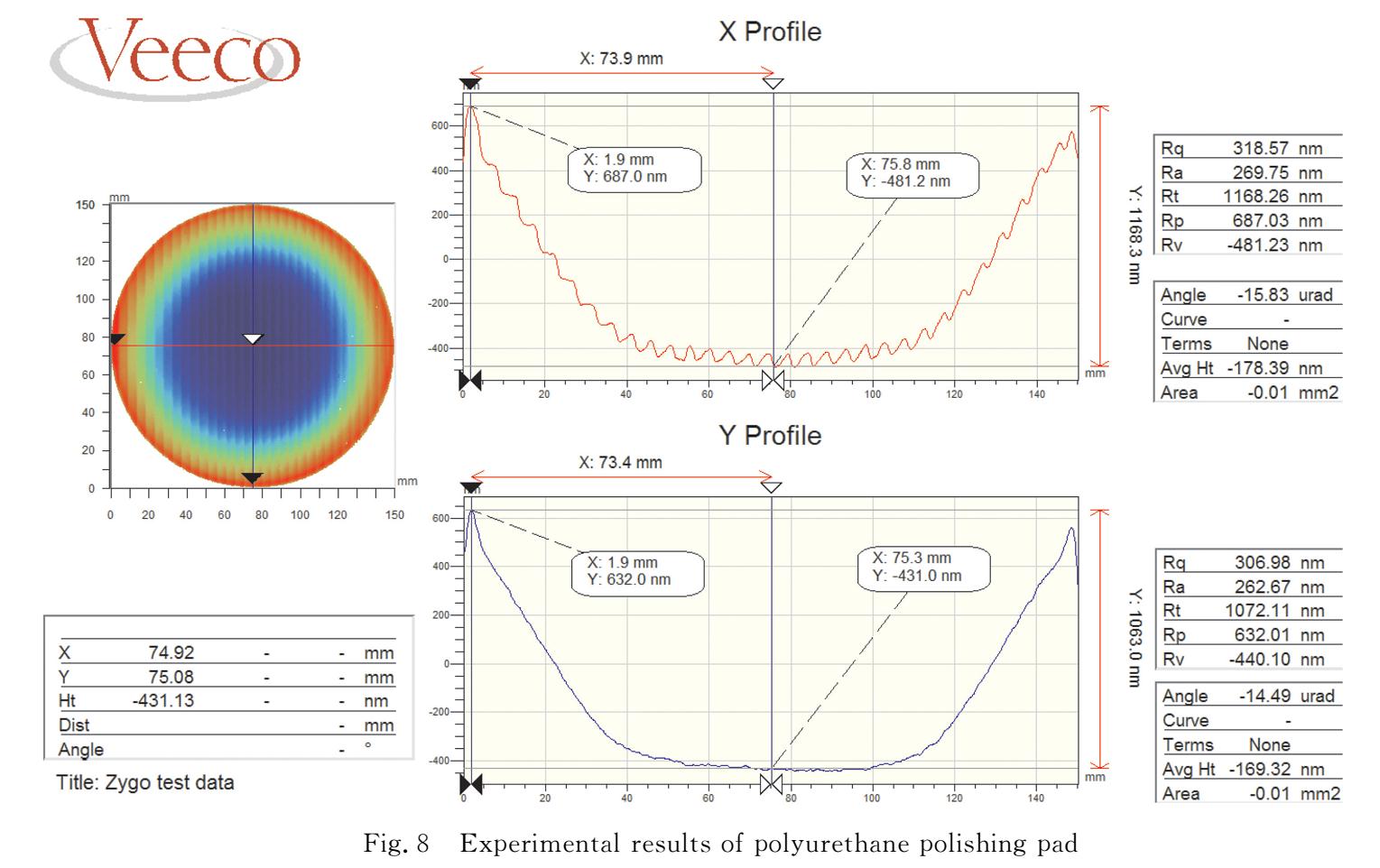
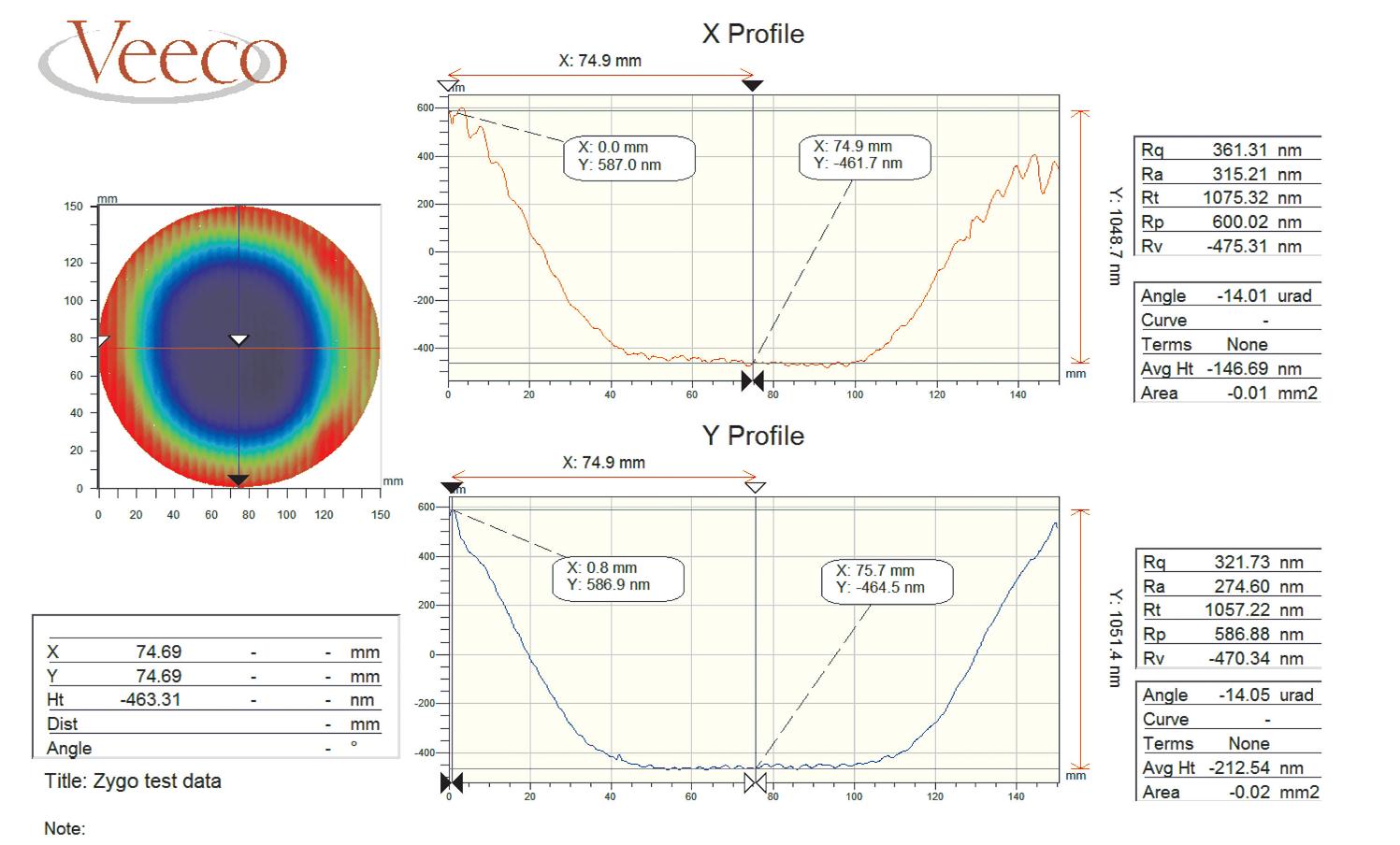
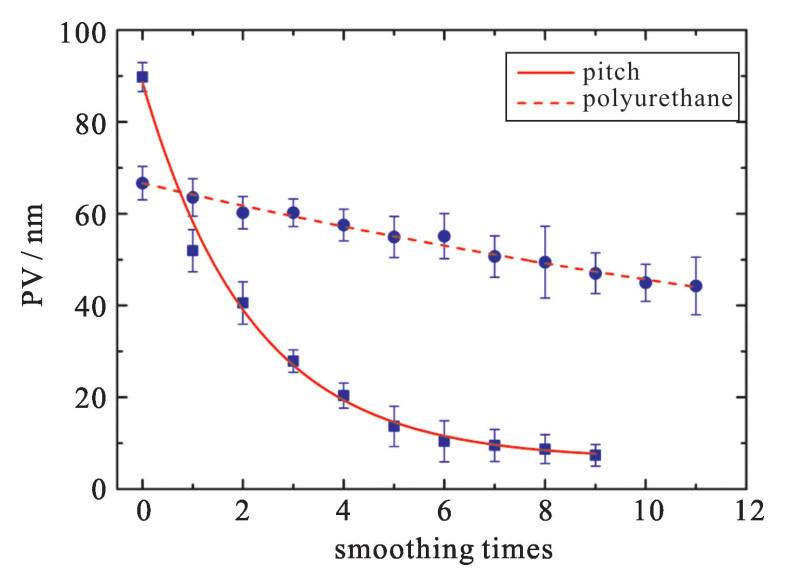
从图 8~9对比能够看出，在总的去除深度相近的情况下(1100 nm左右)，沥青抛光盘加工后元件中心区域波纹误差得到了有效抑制，而聚氨酯抛光盘作用后元件表面各处依然存在较为明显的波纹。说明在相同材料去除率下，沥青比聚氨酯具有更高的波纹匀滑能力。整个实验数据与沥青盘抛光实验对比曲线如图 10所示。
图 10 聚氨酯盘与沥青盘匀滑效果对比Figure 10. Comparison of smoothing effects between polyurethane and pitch两次实验在工艺参数相近的情况下，由于沥青材料的弹性模量远大于聚氨酯材料，从而导致其材料因子也大于聚氨酯盘。故而控制工艺参数变量，沥青抛光盘的匀滑过程中匀滑效率高于聚氨酯抛光盘的，这与理论模拟的匀滑曲线趋势一致。
3. 结论
(1) 根据参数化匀滑模型理论，结合数控抛光的去除函数，能够建立一个多参数的匀滑演化模型。该模型中，元件表面波纹误差是随抛光时间呈指数型收敛的。匀滑效率由材料因子以及抛光盘体积去除率等工艺参数组成。通过模拟分析，对比了理论模型在不同参数下的匀滑效率。在不同抛光盘材料的匀滑过程中，材料因子越大，其整体匀滑效率越高，波纹的收敛曲线下降越快。同样，不同转速下抛光盘的体积去除率越大，对表面误差的匀滑效率也会越高。
(2) 通过选取具有不同空间周期波纹误差(3，5，7 mm)的实验元件，在相同的抛光参数下进行连续抛光实验，由实验数据拟合曲线可由看出，初始表面波纹空间频率会对匀滑效率产生影响，具有较大空间频率的波纹匀滑效率会更高，收敛曲线下降得更快。
(3) 不同材料抛光盘的匀滑效率存在一定差异，根据沥青盘和聚氨酯盘在相同工艺参数下的匀滑实验对比能够看出，沥青材料在波纹匀滑效率上远高于聚氨酯材料。因此在中高频误差的元件中采用沥青盘一般具有较好的匀滑效果。
-
图 2 抛光盘半径25 mm，偏心距5 mm，公转160 r/min，自转8 r/min参数下理论去除函数
Figure 2. Theoretical TIF under the parameters of radius 25 mm, eccentricity 5 mm, revolution 160 r/min and rotation 8 r/min
图 3 抛光盘在具有波纹误差的工件表面接触示意图以及实际抛光平台
Figure 3. A pitch polishing pad contact on the workpiece with ripple error and the experiment platform
图 4 沥青抛光盘与聚氨酯抛光盘匀滑过程理论曲线对比
Figure 4. Theoretical smoothing curves of pitch pad and polyurethane pad
图 5 不同抛光盘转动参数下理论去除函数对比
Figure 5. Comparison of theoretical TIF of different rotation parameters
图 6 不同抛光盘转动参数匀滑过程理论曲线对比
Figure 6. Comparison of theoretical smoothing curves of different rotation parameters
图 7 不同空间周期波纹误差匀滑实验数据拟合曲线
Figure 7. Data points and the fitting curves of the three workpieces with different spatial-period ripple error in the smoothing experiment
-
[1] Jones R A. Optimization of computer controlled polishing[J]. Applied Optics, 1977, 16(1): 218-224. doi: 10.1364/AO.16.000218 [2] Nelson J, Sanders G H. The status of the Thirty Meter Telescope project[C]//Proc of SPIE. 2008: 70121A. [3] Johns M, Mccarthy P, Raybould K, et al. Giant Magellan Telescope: Overview[C]//Proc of SPIE. 2012: 84441H. [4] Wagner R E, Shannon R R. Fabrication of aspherics using a mathematical model for material removal[J]. Applied Optics, 1974, 13(7): 1683-1689. doi: 10.1364/AO.13.001683 [5] 王毅, 倪颖, 余景池. 小型非球面数控抛光技术的研究[J]. 光学精密工程, 2007, 15(10): 1527-1533. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200710013.htmWang Yi, Ni Ying, Yu Jingchi. Computer-controlled polishing technology for small aspheric lens. Optics and Precision Engineering, 2007, 15(10): 1527-1533 https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200710013.htm [6] Wang Zhenzhong, Peng Yunfeng, Guo Yinbiao, et al. Modeling of the static tool influence function of bonnet polishing based on FEA[J]. Int J Adv Manuf Techno, 2014, 74: 341-349. doi: 10.1007/s00170-014-6004-3 [7] Dong Zhichao, Cheng Haobo, Tam Honyuen. Modified subaperture tool influence functions of a flat-pitch polisher with reverse-calculated material removal rate[J]. Applied Optics, 2014, 53(11): 2455-2464. doi: 10.1364/AO.53.002455 [8] Nelson D G, Gould A, Klinger C, et al. Incorporating VIBE into the precision optics manufacturing process[C]//Proc of SPIE. 2011: 812613. [9] 李徐钰, 魏朝阳, 徐文东, 等. 随动压力分布下的非球面抛光去除函数[J]. 光学 精密工程, 2016, 24(12): 3061-3067. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201612027.htmLi Xuyu, Wei Chaoyang, Xu Wendong, et al. Tool influence function in aspheric polishing under dynamic pressure distribution. Optics and Precision Engineering, 2016, 24(12): 3061-3067 https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201612027.htm [10] 王佳, 范斌, 万勇建, 等. 一种评价CCOS抛光工艺误差抑制能力的方法[J]. 光子学报, 2014, 43: 722002. https://www.cnki.com.cn/Article/CJFDTOTAL-GZXB201407035.htmWang Jia, Fan Bin, Wan Yongjian, et al. A method to evaluate the error restraint ability of CCOS process. Acta Photonica Sinica, 2014, 43: 722002 https://www.cnki.com.cn/Article/CJFDTOTAL-GZXB201407035.htm [11] Mehta A P K, Hufnagel R E. Pressure distribution under flexible polishing tools: I. Conventional aspheric optics[C]//Proc of SPIE. 1990, 1303: 178-188. [12] Mehta P K, Reid P B, Derby E A, et al. A mathematical model for optical smoothing prediction of high-spatial-frequency surface errors[C]//Proc of SPIE. 1999, 3786: 447-459. [13] Nie Xuqing, Li Shenyi, Shi Feng, et al. Generalized numerical pressure distribution model for smoothing polishing of irregular midspatial frequency errors[J]. Applied Optics, 2014, 53(6): 1020-1027. doi: 10.1364/AO.53.001020 [14] Kim D W, Park W H, An H K, et al. Parametric smoothing model for visco-elastic polishing tools[J]. Optics Express, 2010, 18(21): 22515-22526. doi: 10.1364/OE.18.022515 [15] Kim D W, Martin H, Burge J H. Control of mid-spatial-frequency errors for large steep aspheric surfaces[C]//Optical Fabrication & Testing. 2012. [16] Shu Yong, Nie Xuqing, Shi Feng, et al. Smoothing evolution model for computer controlled optical surfacing[J]. Journal of Optical Technology, 2014, 81(3): 164-167. doi: 10.1364/JOT.81.000164 期刊类型引用(1)
1. 许乔，陈贤华，汪圣飞，钟波，谢瑞清，王健. 高功率激光光学元件超精密制造技术. 光学学报. 2022(17): 203-221 . 
百度学术其他类型引用(3)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 1284
- HTML全文浏览量: 261
- PDF下载量: 64
- 被引次数: 4
