JEMS-FDTD软件在电磁脉冲区域传播数值模拟中的应用

鲍献丰; 李瀚宇; 伍月千; 周海京

doi:10.11884/HPLPB201931.190200

JEMS-FDTD软件在电磁脉冲区域传播数值模拟中的应用

doi: 10.11884/HPLPB201931.190200

鲍献丰^{1, 2,},
李瀚宇^{2, 3},
伍月千^{1, 2},
周海京^{2, 3}

1.
中物院高性能数值模拟软件中心, 北京 100088
2.
中国工程物理研究院复杂电磁环境科学与技术重点实验室, 四川绵阳 621900
3.
北京应用物理与计算数学研究所, 北京 100094

基金项目:

国防基础科研计划资助项目 C1520110002

国家自然科学基金项目 61771061

详细信息

作者简介:
鲍献丰(1986—), 男, 硕士, 从事高性能电磁计算研究; bobbao0925@163.com

中图分类号: TN248.6
计量
- 文章访问数: 1267
- HTML全文浏览量: 288
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2019-06-04
- 修回日期: 2019-08-12
- 刊出日期: 2019-10-15

Application of JEMS-FDTD in EMP regional propagation simulation

Bao Xianfeng^{1, 2
,},
Li Hanyu^{2, 3},
Wu Yueqian^{1, 2},
Zhou Haijing^{2, 3}

1.
CAEP Software Center for High Performance Numerical Simulation, Beijing 100088, China
2.
Complicated Electromagnetic Environment Laboratory of China Academy of Engineering Physics, Mianyang 621900, China
3.
Institute of Applied Physics and Computational Mathematics, Beijing 100094, China

摘要

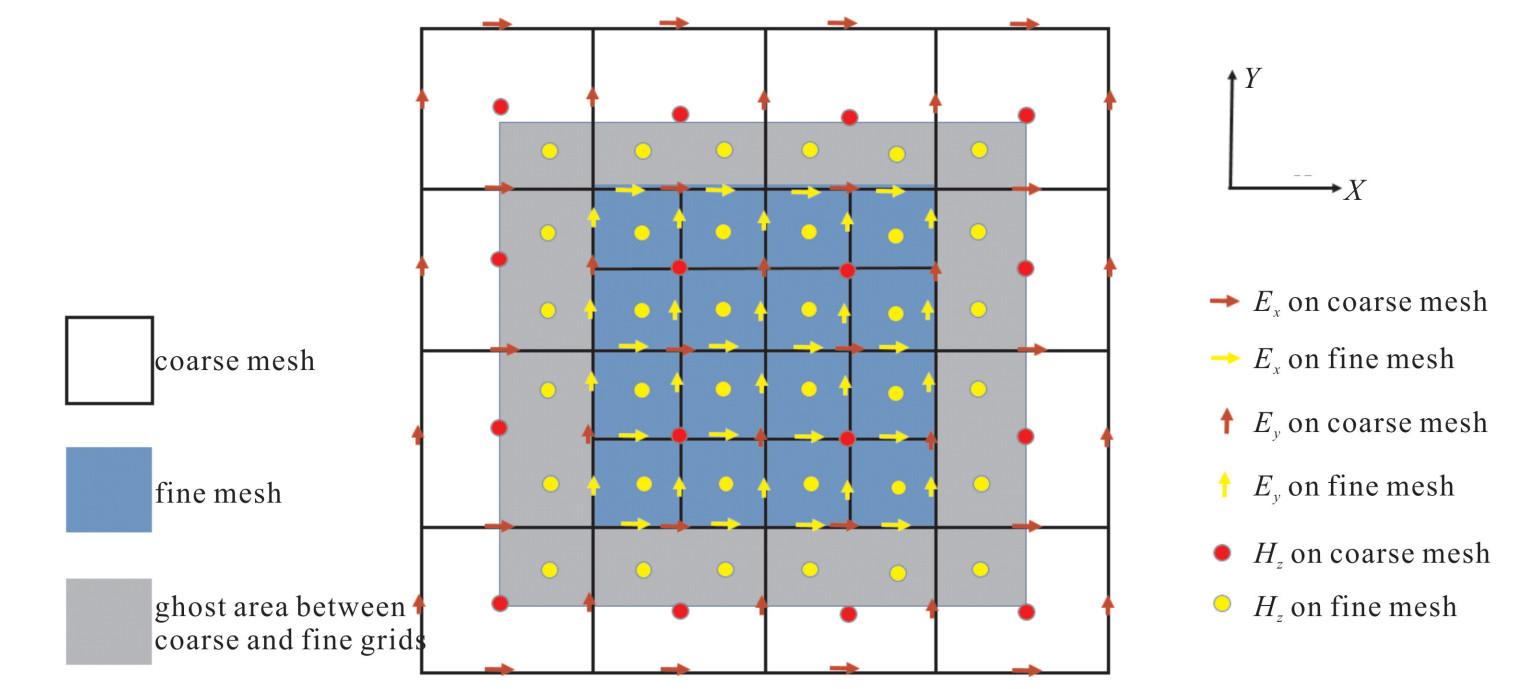
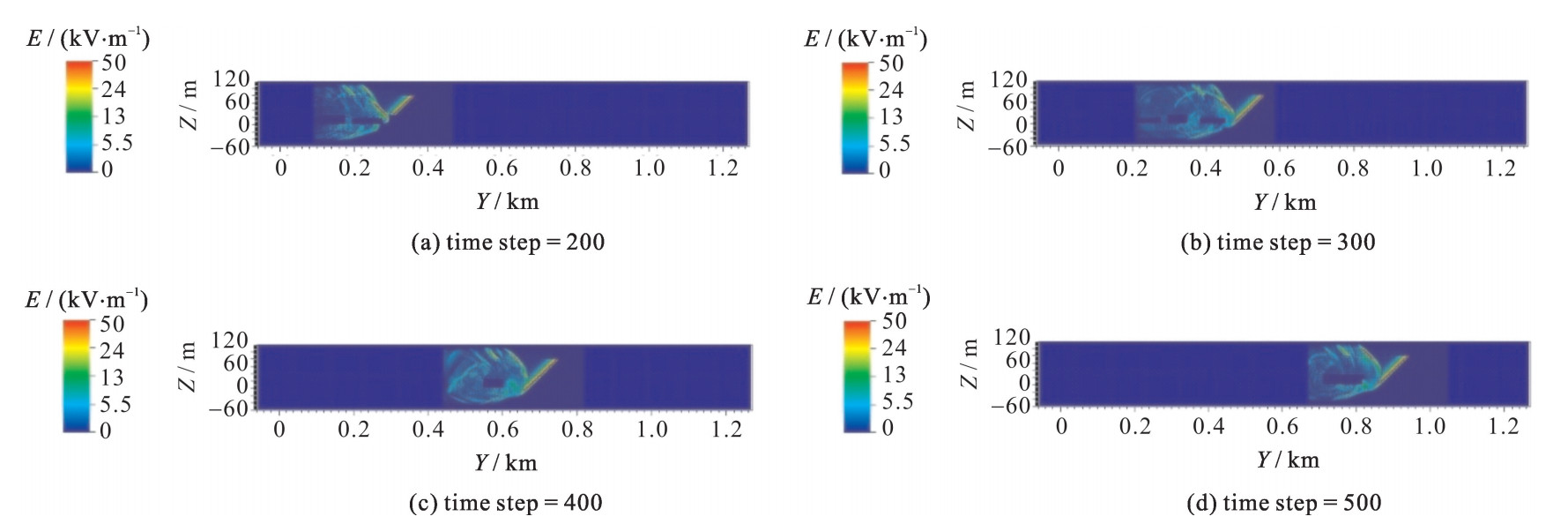
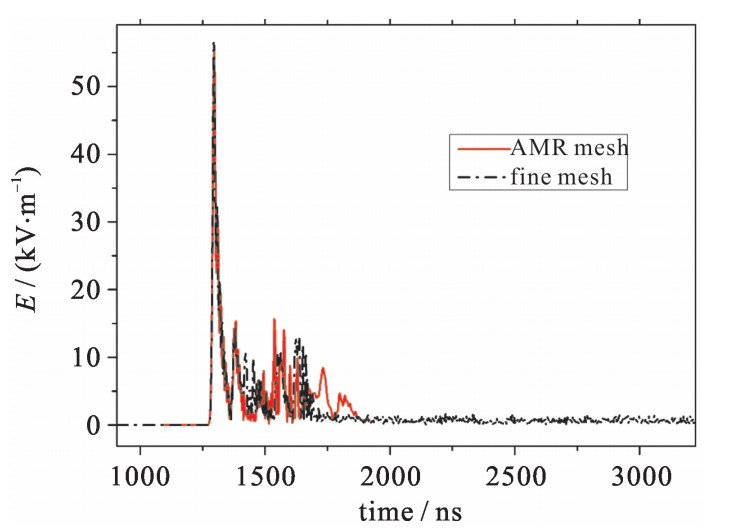
摘要: 电磁脉冲区域传播数值模拟是电磁环境效应分析的重要环节, 面临空间尺度巨大、多辐射源、复杂地貌等技术挑战。本文介绍了三维时域全波电磁模拟并行软件JEMS-FDTD的研制进展。在大规模并行计算FDTD方法的基础上结合自适应网格技术, 研制了一种适应于大区域电磁脉冲传播的高效时域全波计算方法。并基于该技术实现了千km²级城市电磁脉冲区域传播的数值模拟, 获取了全空间的时域电磁场信息, 验证了软件在电磁脉冲区域传播仿真应用中的可行性。
- 时域有限差分方法 /
- 电磁脉冲 /
- 区域传播 /
- 自适应网格 /
- 数值模拟
Abstract: Numerical simulation of electromagnetic pluses regional propagation is an important link in the analysis of electromagnetic environment effect, faced with technical challenges such as huge spatial scale, multiple radiation sources and complex geomorphology.This paper demonstrates a massively parallel 3 Dfull-wave electromagnetic field simulation program software JEMS-FDTD and its development progress.Based on the large-scale parallel FDTD method and adaptive mesh refinement technology, an efficient full-wave time-domain computation method for large-area electromagnetic pulse propagation is developed.The numerical simulation of regional propagation of electromagnetic pulse in 1000 square kilometers city has been realized.This work verifies the feasibility of the software in the simulation of electromagnetic pluses regional propagation.
- FDTD /
- EMP /
- regional propagation /
- adaptive mesh refinement /
- numerical simulation

HTML全文

图 1 多层自适应网格示意

Figure 1. View of adaptive grid

下载: 全尺寸图片幻灯片

图 2 时间细化模式

Figure 2. Time refinement model

下载: 全尺寸图片幻灯片

图 3 粗细网格电磁场分量排布

Figure 3. Arrangement of EM field in coarse and fine grids

下载: 全尺寸图片幻灯片

图 4 时域电场分布

Figure 4. Time domain electric field distribution

下载: 全尺寸图片幻灯片

图 5 全局细网格与自适应网格方法计算空间点时域波形对比

Figure 5. Comparison between global fine grids and adaptive mesh refinement method for time domain waveform

下载: 全尺寸图片幻灯片

图 6 城市模型示意图

Figure 6. View of city model

下载: 全尺寸图片幻灯片

图 7 时域电场分布

Figure 7. Time domain electric field distribution

下载: 全尺寸图片幻灯片

参考文献(10)

[1]	刘尚合. 武器装备的电磁环境效应及其发展趋势[J]. 装备学院学报, 2005, 16(1): 1-6. doi: 10.3783/j.issn.1673-0127.2005.01.001 Liu Shanghe. Effect of electromagnetic environment to weaponry and its trend of development. Journal of the Academy of Equipment Command & Amp, 2005, 16(1): 1-6 doi: 10.3783/j.issn.1673-0127.2005.01.001
[2]	孙国至, 刘尚合, 陈京平, 等. 战场电磁环境效应对信息化战争的影响[J]. 军事运筹与系统工程, 2006, 20(3): 43-47. doi: 10.3969/j.issn.1672-8211.2006.03.010 Sun Guozhi, Liu Shanghe, Chen Jingping, et al. The effect of battlefield electromagnetic environment on information warfare. Military Operations Research and Systems Engineering, 2006, 20(3): 43-47 doi: 10.3969/j.issn.1672-8211.2006.03.010
[3]	张青洪, 廖成, 盛楠, 等. 森林环境电波传播抛物方程模型的改进研究[J]. 物理学报, 2013, 62(20): 189-195. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201320025.htm Zhang Qinghong, Liao Cheng, Sheng Nan, et al. Improved study on parabolic equation model for radio wave propagation in forest. Acta Physica Sinica, 2013, 62(20): 000189-195 https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201320025.htm
[4]	申荣. 小区域的电磁环境评价研究[D]. 西安: 西安电子科技大学, 2006. Shen Rong. Study on evaluation of electromagnetic environment in small area. Xi'an: Xidian University, 2006
[5]	刘艳梅. 基于射线追踪法的电磁环境仿真系统实现的关键技术研究[D]. 北京: 北京邮电大学, 2013. Liu Yanmei. Research on key technologies for realization of electromagnetic environment simulation system based on ray tracing method. Beijing: Beijing University of Posts and Telecommunications, 2013
[6]	Li Hanyu, Zhou Haijing, Liu Yang, et al. Massively parallel FDTD program JEMS-FDTD and its applications in platform coupling simulation[C]//IEEE International Symposium on Electromagnetic Compatibility (EMC Europe). 2014: 229-233.
[7]	李瀚宇, 周海京, 廖成. 时域全波电磁计算程序JEMS-FDTD在复杂电磁环境研究中的应用[J]. 强激光与粒子束, 2014, 26: 073213. doi: 10.11884/HPLPB201426.073213 Li Hanyu, Zhou Haijing, Liao Cheng. Application of JEMS-FDTD in complicated electromagnetic environment study. High Power Laser and Particle Beams, 2014, 26: 073213 doi: 10.11884/HPLPB201426.073213
[8]	鲍献丰, 李瀚宇, 伍月千, 等. JEMS-FDTD软件在飞机HIRF仿真中的应用[J]. 强激光与粒子束, 2017, 29: 103204. doi: 10.11884/HPLPB201729.170175 Bao Xianfeng, Li Hanyu, Wu Yueqian, Application of JEMS-FDTD in HIRF simulation on aircraft. High Power Laser and Particle Beams, 2017, 29: 103204 doi: 10.11884/HPLPB201729.170175
[9]	徐小文, 莫则尧, 刘青凯, 等. 自适应结构网格上扩散方程隐式时间积分算法及其应用[J]. 计算物理, 2012, 29(5): 684-692. doi: 10.3969/j.issn.1001-246X.2012.05.008 Xu Xiaowen, Mo Zeyao, Liu Qingkai, et al. An implicit time-integration algorithm for diffusion equations with structured AMR and applications. Chinese Journal of Computational Physics, 2012, 29(5): 684-692 doi: 10.3969/j.issn.1001-246X.2012.05.008
[10]	莫则尧. 并行自适应结构网格应用支撑软件框架研制进展[C]//中国工程物理研究院科技年报. 2009: 61-62. Mo Zeyao. Development of jparallel adaptive structured mesh applications infrastructure//Annual Report of Science and Technology of China Academy of Engineering Physics, 2009: 61-62