Digital self-excited vertical test system of superconducting cavity
-
摘要:
基于数字自激算法设计并实现的超导腔垂直测试系统提高了超导腔的垂直测试效率，为先进光源技术研发与测试平台（PAPS）的超导腔批量化生产提供了重要保障；垂直测试系统的射频前端和时钟分配系统采用了二次上下变频方案，可以在一定范围内灵活设置测试系统自激环路的工作频率，增大了该测试系统的工作带宽。利用此系统完成了1.3 GHz 9-cell超导腔的通带频率测试，结果表明，该测试系统能有效避免不同模式之间的串扰，具备较强的频率分辨能力（＜800 kHz），保证多单元超导腔性能验证的进行。
Abstract:Vertical test is an important method for characterizing the performance of superconducting cavities. We designed an superconducting cavity vertical test system based on digital self-excited algorithm and the technology of low-level radio frequency, which could improve the vertical test efficiency of superconducting cavities. The RF front-end and clock distribution system of the vertical test system adopts the second up-and-down conversion scheme. To some extent, the working frequency of the digital self-excited loop of the vertical test system can be set flexibly, and the working bandwidth of the test system is increased. The test results of the pass-band frequency of the 1.3 GHz 9-cell superconducting cavity show that the vertical test system has strong frequency resolution (＜800 kHz) to ensure the smooth progress of the multi-cell superconducting cavity pass-band test.
-
先进光源技术研发与测试平台（PAPS）的超导高频系统是配备后处理、组装及测试设备的超导高频实验室，将具备超导腔的批量处理及测试能力，为未来国内大型超导加速器建设提供有力支撑。各超导加速器所采用的超导腔频率因为设计目标不同而有所区别：上海硬X射线自由电子激光的超导腔频率主要为1.3 GHz和3.9 GHz；高能同步辐射光源的超导腔频率为166.6 MHz和500 MHz；环形正负电子对撞机的超导腔频率为650 MHz和1.3 GHz。垂直测试是验证超导腔性能的重要手段[1]，测试系统的设计需要充分考虑到超导腔的频率范围。
20世纪70年代，Jean Delayen首次将基于放大器的自激原理应用于超导腔的幅度、相位控制[2]，经过数十年的发展，国外的著名加速器实验室如Thomas Jefferson National Accelerator Facility[3]和European Spallation Source[4-5]等均已建成数字自激的垂直测试系统，系统已具备大批量超导腔垂直测试的能力。国内的超导腔垂直测试研究起步较晚：2013年，为满足ADS 项目Spoke超导腔的测试需求，中国科学院高能物理研究所首先建成基于模拟自激的垂直测试系统[6]；中国科学院兰州近代物理研究所至今所使用的仍然是传统的、基于压控振荡锁相环的模拟垂直测试系统[7]。由于模拟测试系统的带宽和自动化能力受限、且在进行多单元超导腔的通带测试时难以将频率间隔较小（小于1 MHz）的模式区分开，制约了超导腔垂直测试系统的批量化测试能力。综合考虑垂直测试过程中可能的超导腔频率范围和实际的批量化测试需求，本文不仅设计实现了数字自激垂直测试系统以提高超导腔测试效率，而且采用二次变频方案实现的射频前端和时钟分配系统可以灵活设置测试系统中数字自激环路的工作频率，使单通道的数字自激垂直测试系统具备了足够的工作带宽。
1. 自激环路
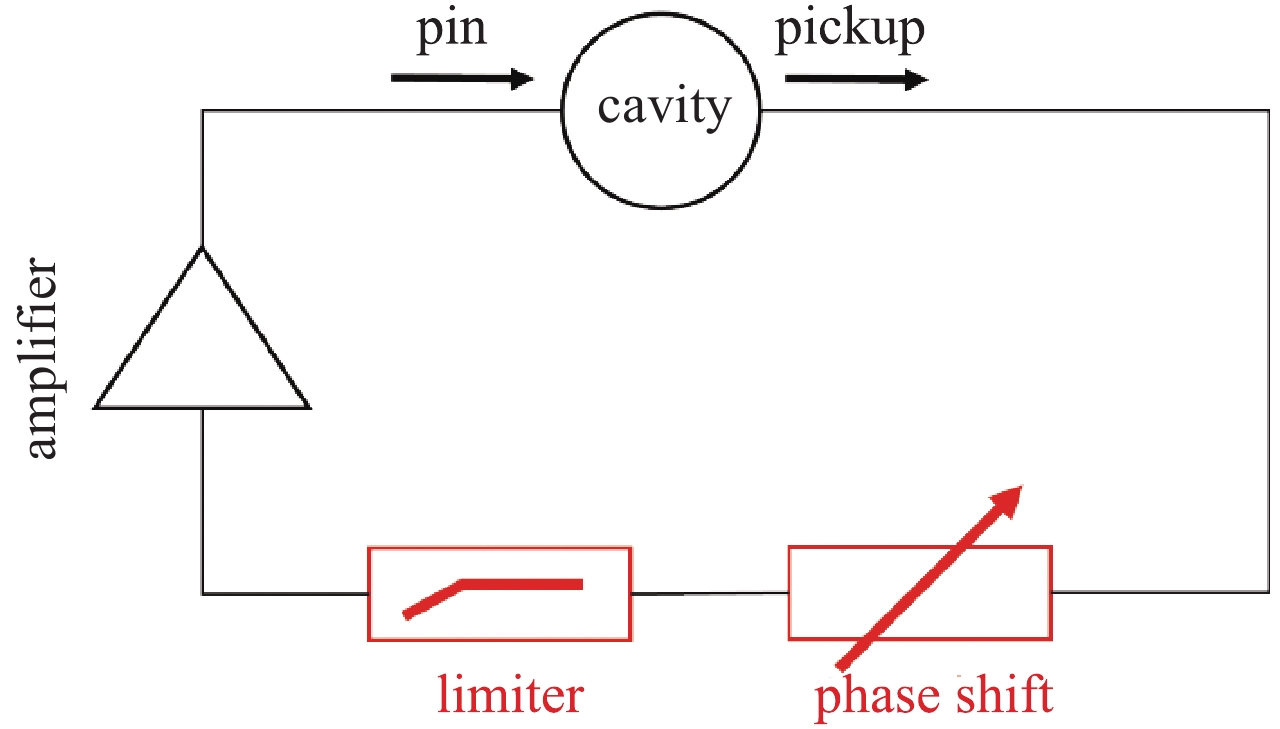
典型的自激环路如图1所示。将超导腔视为滤波器，并增加移相器、限幅器以及环路放大器，即组成基本的自激环路。
如果放大器的增益大于环路中的损耗，放大器的噪声将会被放大、最终成为环路中的信号，该信号的幅度通过环路中的限幅器来控制。超导腔的中心频率和带宽决定了哪些频率的信号可以通过超导腔。通过超导腔的相移记为
${\theta _{\rm{c}}}(\omega )$ ，环路其余部分的相移为${\theta _{\rm{l}}}(\omega )$ ，当它们的和为2π的整数倍（如式（1）所示）且环路增益大于1时，环路出现自激振荡现象，自激振荡的信号角频率为ω[2]，有θc(ω)+θl(ω)=2πn (1) 式中：n为整数。
在数字域中实现图1所示的移相器和限幅器，即为基本的数字自激环路。
2. 射频前端及时钟分配系统
超导腔垂直测试过程中，数字自激垂直测试系统进行幅度、相位控制的前提是待鉴相的环路信号和数字信号处理板的参考时钟信号锁相。垂直测试系统中自激环路的信号频率由待测试超导腔的谐振频率和带宽决定，但即使测试对象都是1.3 GHz的单单元腔，不同的腔之间也会存在一定的频率差，根据经验可知，1.3 GHz单单元腔的垂直测试要求测试系统具备（1 300±2） MHz的工作频率范围。另外，考虑到多单元腔如1.3 GHz 9单元腔（π/9模～π模对应的频率范围为1 270～1 300 MHz）进行垂直测试时，有时需要在各个模式下进行通带测试，因此要求测试系统的低电平控制环路也要满足相应的工作频率范围（（1 285±15） MHz）。
综合考虑低电平控制环路的工作频率范围、环路信号与参考时钟信号锁相的需求，射频前端及时钟分配系统的设计采用了二次变频方案。具体如下：首先，由场探针提取的超导腔Pickup信号经功率分配器后得到两个相同频率的信号Pickup-A和Pickup-B。Pickup-A和Pickup-B（假设腔的谐振频率为1.3 GHz）再分别与本振信号源LO的输出（图2（a）中为800 MHz）进行混频、滤波后得到500 MHz的信号，之后，Pickup-A下变频后的500 MHz信号进入CH5通道，而Pickup-B下变频后的500 MHz信号经过限幅器后作为同步信号源Snyc source的相位参考信号，插入限幅器是为了防止超导腔的场探针提取的信号过大导致同步信号源造成损坏（该同步信号源的输出信号为500 MHz，进入Refin通道后一分为二：一路信号经AD9510分频后得到ADC、DAC、FPGA板的时钟以及25 MHz的时钟输出；另一路信号作为射频信号，与AD9510输出的25 MHz时钟混频、滤波后得到475 MHz的中频信号，该475 MHz的信号是第二次下变频和第一次上变频的本振信号）。第二次下变频时（见图2（b）），来自CH5通道的500 MHz信号作为射频信号，与475 MHz的本振信号进行混频、滤波产生25 MHz的中频信号，被时钟为100 MHz的ADC采样后最终进入FPGA板中进行相应的数字信号处理；之后，FPGA的输出经过时钟为100 MHz的DAC及滤波器后得到25 MHz的信号，并通过两次上变频后得到1.3 GHz的信号，最终作为自激环路中固态放大器的输入激励。
图 2 第一次和第二次上下变频原理图Figure 2. Schematic of the first and the second up-and-down frequency conversion整个射频前端及时钟分配系统的关键是本振信号源LO，核心是同步信号源Sync Source（见图2（a））。前者输出770～800 MHz的本振信号时，可以将源自于超导腔内的射频信号（频率1 270～1 300 MHz）变频到统一的500 MHz的信号；后者在环路没有自激时为ADC、DAC和FPGA板提供稳定的时钟信号。当环路自激时同步信号源输出信号与自激环路中的信号锁相，最终能形成稳定的自激环路。
3. 数字自激算法
FPGA板上实现的数字自激算法是整个垂直测试系统的重要组成部分，具体的算法结构如图3所示，25 MHz的中频信号经100 MHz采用时钟的ADC进行奈奎斯特过采样，考虑到IQ正交解调具有较小的延时，故采用该方案以得到正交的IQ信号[8]，再经平均滤波后通过CORDIC算法进行鉴相，之后恢复到IQ域做数字移相，最后由IQ调制经DAC、后续的模拟滤波器输出25 MHz的中频信号。
数字限幅器和数字移相器是垂直测试系统数字自激算法的关键。数字限幅器的实现如图3所示，经CORDIC鉴相后得到的“Phase”信号作为相位，“Set_Amplitude”信号是由上位机给定的幅度信号（即上位机给定限幅值），幅度信号和相位信号经CORDIC坐标变换后得到正交的IQ信号，从而实现数字域的限幅处理。
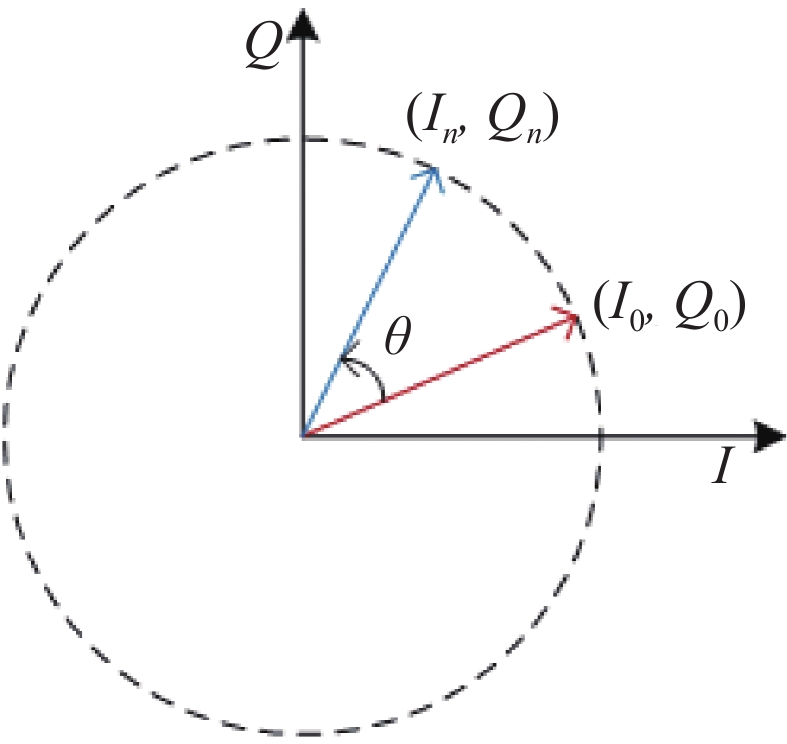
在IQ域内通过坐标旋转可以较容易地实现数字移相功能[9]，如图4所示，
$\left( {{I_0},{Q_0}} \right)$ 移相θ得到$\left( {{I_n},{Q_n}} \right)$ ，对应的坐标旋转如式（2）所示。cosθ和sinθ的值通过16位量化后存储到ROM中，来自上位机的地址值通过查找表的方式来读取实时的cosθ和sinθ值，再将之前限幅、坐标变换后的信号和相应的cosθ和sinθ值做矩阵乘法运算，即实现所需的环路数字移相器。[InQn]=[cosθ−sinθsinθcosθ]⋅[I0Q0] (2) 4. 测试结果及分析
4.1 射频前端线性度测量
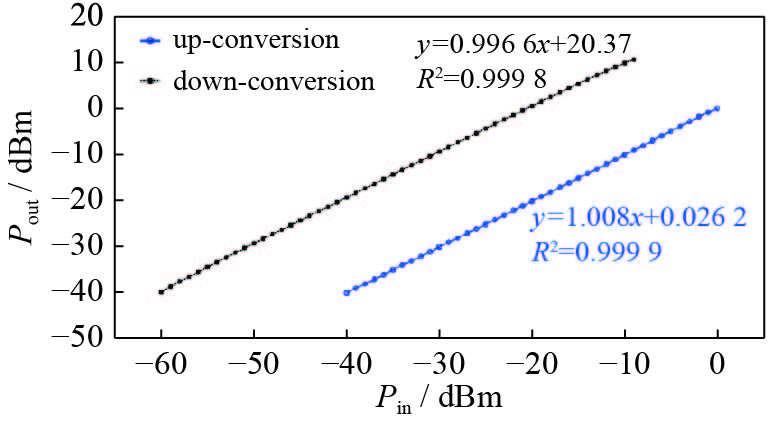
对二次变频方案实现的射频前端线性度测量结果如图5所示（上变频：图2（b）中DAC输出的25 MHz中频信号经二次上变频到1.3 GHz；下变频：图2（a）中1.3 GHz的射频信号Pickup-A经二次下变频到25 MHz）。
图5中，
${R^2}$ 为对测量数据做线性拟合时的决定系数，拟合的结果表明，上、下变频通道均有很好的线性度。此外，上变频通道的增益约为0.02 dB，功率动态范围约40 dB；下变频通道的增益约为20.37 dB，功率动态范围约50 dB。数字自激系统刚启动时，由超导腔场探针提取到的Pickup-A信号很微弱，下变频通道增益大于20 dB可以保证该微弱信号能被ADC采样、进而在垂直测试系统中形成稳定的数字自激环路。4.2 数字自激环路3 dB带宽测量
为了对研制的数字自激垂直测试系统性能进行验证，选择了1支1.3 GHz 9单元超导腔作为测试腔。超导腔降温至2 K后，开启该数字自激垂直测试系统，选择Agilent MSO9254A的示波器对超导腔的信号进行监测，使用Tektronix RSA5106A的频谱分析仪来测量超导腔的场衰减时间τ。
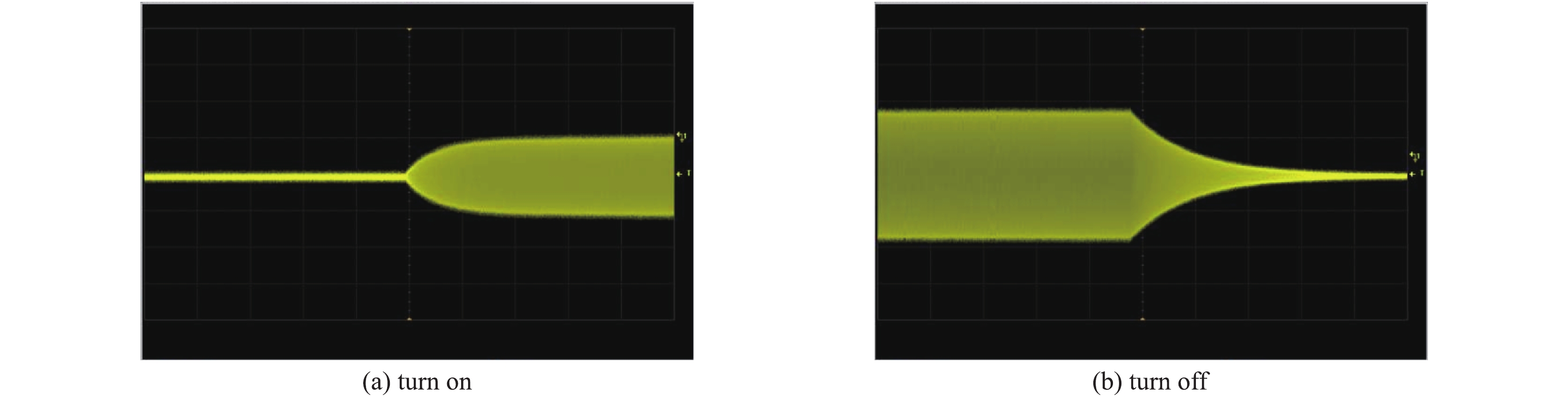
基于上文中所搭建的数字自激垂直测试系统，设置本振信号源LO的频率为800.01 MHz，测试过程中能快速找到超导腔的频率信号，图6（a）和（b）分别是数字自激系统开启和和关闭瞬间示波器监测到的超导腔内信号波形。
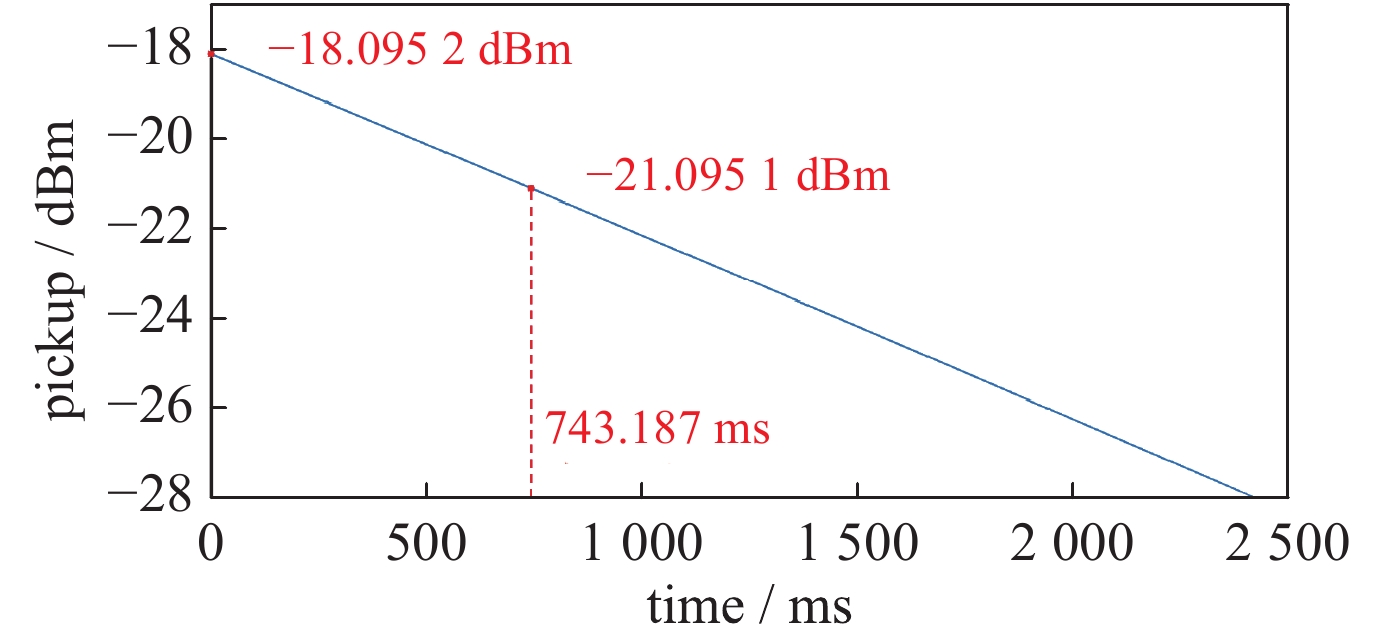
选取合适的电场梯度，当示波器显示的Pickup信号幅度稳定后，关闭数字自激环路的激励输出，通过频谱分析仪测量Pickup信号的衰减时间，结果如图7所示。根据经验，取前10%的时间来获得计算所需的τ值[10-11]，图中当Pickup的信号强度由−18.095 2 dBm衰减3 dB到−21.095 1 dBm时，τ为743.18 ms。此时频率为1 300.017 72 MHz，计算得到超导腔的有载品质因数
${Q_{{\rm{load}}}}$ [12]为8.76×109，对应的自激环路3 dB带宽约为0.148 Hz。4.3 1.3 GHz 9单元超导腔通带频率测量
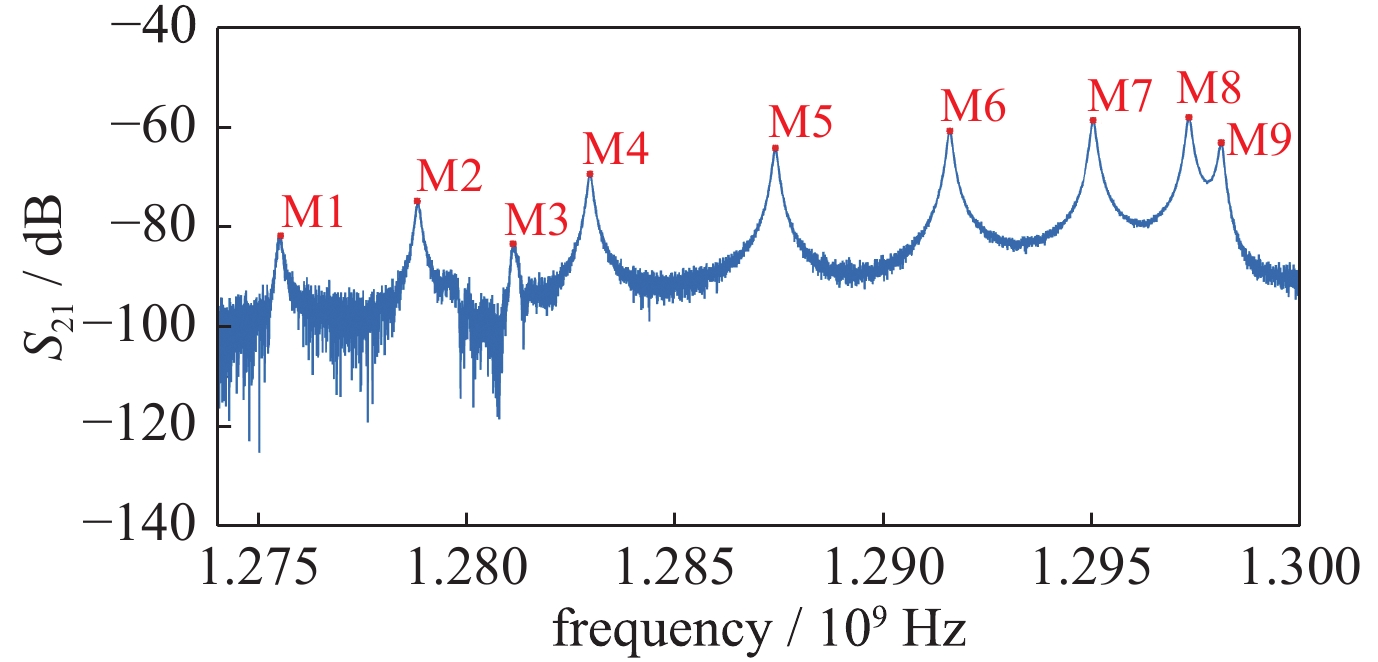
常温下超导腔的Q值较低，使用矢量网络分析仪很容易测得超导腔的通带频率响应如图8所示，其中8π/9模（M8）和π模（M9）的频率较为接近，间隔仅为770 kHz。
降温至2 K时，超导腔的Q值增加、带宽降低，使用矢量网络分析仪很难测得如图8所示的通带频率响应。基于文中所搭建的数字自激垂直测试系统，灵活设置图2（a）中本振信号源LO的输出频率，分别将数字自激环路中信号的频率锁定为超导腔各个模式的谐振频率，频谱分析仪测得各模式的谐振频率如表1所示。
表 1 1.3 GHz 9单元超导腔通带频率测试Table 1. Pass-band mode frequency of 1.3 GHz 9-cell superconducting cavitymode frequency/MHz temperature is 298.15 K temperature is 2 K π/9 1 275.515 80 1 277.384 00 2π/9 1 278.776 20 1 280.695 08 3π/9 1 281.090 20 1 283.006 44 4π/9 1 282.928 40 1 284.837 76 5π/9 1 287.449 80 1 289.295 32 6π/9 1 291.568 20 1 293.490 92 7π/9 1 295.010 60 1 296.945 96 8π/9 1 297.301 20 1 299.237 56 π 1 298.076 00 1 300.017 72 由于降温过程中超导腔发生形变，低温下超导腔各模式的谐振频率会略微增大，但各模式间的频率间隔基本保持一致。表1中，温度为2 K时测得超导腔π/9模和π模的频率分别为1 299.237 56 MHz和1 300.017 72 MHz，间隔约为780 kHz，和常温时测得的频率间隔770 kHz基本一致。通带频率测量的结果表明，温度对各个模式谐振频率的频率间隔影响很小，超导腔垂直测试时可在常温下预先使用矢量网络分析仪测量超导腔的通带频率，得出各个模式间的频率间隔，为2 K下的低温测试和本振信号源频率设定提供指导。
低温下超导腔的通带测试有利于对超导腔性能的诊断和缺陷的定位，已有的模拟自激垂直测试系统受限于模拟滤波器带宽、难以分辨频率间隔小于5 MHz的两个模式，测试过程中相邻的模式常常混叠在一起，影响测试进度、甚至无法进行通带测试。表1中测试结果表明，基于数字自激环路实现的垂直测试系统可以相对容易地实现满足带宽要求的滤波器，进而将频率间隔不到800 kHz的两个模式区分开（8π/9模和π模的频率间隔约780 kHz）。
5. 结 论
本文基于数字自激算法研制了数字自激的超导腔垂直测试系统，采用二次上下变频方案完成了射频前端和时钟分配系统的设计，并将此系统成功应用于1.3 GHz超导腔的垂直测试：（1）射频前端的输入信号和输出信号线性度良好，且上、下变频有足够的功率动态范围；（2）环路带宽的测量结果间接表明，数字自激环路可以在高品质因数的超导腔中激励起稳定的电磁场；（3）2 K低温下1.3 GHz 9单元超导腔的通带模式频率测量结果表明，该测试系统可实现不同频率的自激环路中射频信号和FPGA时钟之间的锁相，并且该测试系统具备测试所需的工作带宽和超导腔通带模式分辨能力。
致 谢 感谢中国科学院高能物理研究所王光伟研究员以及高频组所有同事给予的帮助。
-
图 2 第一次和第二次上下变频原理图
Figure 2. Schematic of the first and the second up-and-down frequency conversion
表 1 1.3 GHz 9单元超导腔通带频率测试
Table 1. Pass-band mode frequency of 1.3 GHz 9-cell superconducting cavity
mode frequency/MHz temperature is 298.15 K temperature is 2 K π/9 1 275.515 80 1 277.384 00 2π/9 1 278.776 20 1 280.695 08 3π/9 1 281.090 20 1 283.006 44 4π/9 1 282.928 40 1 284.837 76 5π/9 1 287.449 80 1 289.295 32 6π/9 1 291.568 20 1 293.490 92 7π/9 1 295.010 60 1 296.945 96 8π/9 1 297.301 20 1 299.237 56 π 1 298.076 00 1 300.017 72 
下载: 导出CSV
-
[1] Powers T. Theory and practice of cavity RF test system[C]//Proceedings of the 12th International Workshop on RF Superconductivity. 2005: 40-70. [2] Delayen J R. Phase and amplitude stabilization of superconducting resonators[D]. California: California Institute of Technology, 1978: 1-16. [3] Allison T, Delayen J R, Hovater C, et al. A digital self excited loop for accelerating cavity field control[C]//Proceedings of PAC07. 2007: 2481-2483. [4] Goryashko V A, Bhattacharyya A K, Li Han, et al. A method for high-precision characterization of the Q-slope of superconducting RF cavities[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(11): 3764-3771. doi: 10.1109/TMTT.2016.2605671 [5] Nicander H. Electro-acoustic stability of a superconducting spoke cavity[D]. Sweden: Uppsala University, 2015: 31-37. [6] 张娟, 戴建枰, 黄泓, 等. 基于Labview 的超导腔测试数据采集系统[J]. 核电子学与探测技术, 2013, 33(9):1098-1103. (Zhang Juan, Dai Jianping, Huang Hong, et al. Data acquisition system of superconducting cavity test based on Labview[J]. Nuclear Electronics & Detection Technology, 2013, 33(9): 1098-1103 doi: 10.3969/j.issn.0258-0934.2013.09.014 [7] 常玮. 低beta超导腔体的测试研究[D]. 兰州: 中国科学院近代物理研究所, 2014: 62-68.Chang Wei. Research on low beta superconducting cavity testing[D]. Lanzhou: Institute of Modern Physics, Chinese Academy of Sciences, 2014: 62-68 [8] 邱丰. 1.3 GHz 9-cell腔数字化低电平系统的研究[D]. 北京: 中国科学院高能物理研究所, 2012: 76-77.Qiu Feng. Study on the digital low level RF control system of 1.3 GHz nine-cell cavity[D]. Beijing: Institute of High Energy Physics, Chinese Academy of Sciences, 2012: 76-77 [9] 张志刚. 同步辐射光源增强其高频数字化低电平系统研制[D]. 上海: 中国科学院 上海应用物理研究所, 2015: 68-72.Zhang Zhigang. Development of digital low level RF system for booster at Synchrotron Radiation Light Source[D]. Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2015: 68-72 [10] Holzbauer J P, Pischalnikov Y, Sergatskov D A, et al. Systematic uncertainties in RF-based measurement of superconducting cavity quality factors[J]. Nuclear Instruments and Methods in Physics Research A, 2016, 830: 22-29. doi: 10.1016/j.nima.2016.05.025 [11] Holzbauer J P, Contreras C, Pischalnikov Y, et al. Improved RF measurements of SRF cavity quality factors[J]. Nuclear Instruments and Methods in Physics Research A, 2019, 913: 7-14. doi: 10.1016/j.nima.2018.09.155 [12] 刘亚萍. BEPCII 500 MHz 铌腔的研制[D]. 北京: 中国科学院高能物理研究所, 2011: 94-95.Liu Yaping. Study of BEPCII 500 MHz niobium cavity[D]. Beijing: Institute of High Energy Physics, Chinese Academy of Sciences, 2011: 94-95 期刊类型引用(1)
1. 冯立文，王芳，林林，郝建奎. 超导腔垂直测试数字化自激励环路研制. 强激光与粒子束. 2021(02): 88-93 . 
本站查看其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 1874
- HTML全文浏览量: 693
- PDF下载量: 129
- 被引次数: 2
