Hybrid algorithm of radio wave propagation based on parabolic equation in cylindrical coordinates and method of moments
-
摘要:
针对包含近源障碍物条件下的电波传播问题,提出了一种新颖的电波传播预测混合建模方法:矩量法(MOM)和圆柱坐标系抛物方程法(PEM)混合建模方法(MOM-PEM);MOM用于包含辐射源和近源障碍物的小圆柱区域内的电波传播建模,PEM用于MOM计算空间外的大区域范围内电波传播建模。MOM和PEM的计算过渡区域进行精细化网格剖分处理以避免场强数值传递的不兼容。仿真模拟了三类近源障碍物存在场景下的电波传播问题:有限开窗屏障碍物、立方体障碍物以及包含辐射源的半封闭空间障碍物,并将混合算法计算得到的结果和相同环境下采用全矩量法计算得到的结果进行了数值对比,结果表明混合算法和矩量法在精度上吻合较好。
Abstract:In this paper, a novel hybrid modeling method is proposed for radio wave propagation prediction. This method is based on parabolic equation in cylindrical coordinates and method of moments. The method of moments is used to model the radio wave propagation in the small cylindrical region containing the radiation source and the near source obstacle, and the parabolic equation in cylindrical coordinate system is used to model the radio wave propagation in a large region outside method of moments region. The transition surface between method of momenst and parabolic equation is carefully treated to avoid the incompleteness of numerical calculation. The hybrid algorithm proposed in this paper is suitable for predicting the radio wave propagation under various conditions, and it is applied for three different scenarios: the near source region contains a finite windowed obstacle, a finite cube obstacle and a semi-closed cube space obstacle. The calculation results of the hybrid algorithm are compared to those obtained from full method of moment implementations of the same scenarios to verify its accuracy.
-
在无线电传输系统中,复杂的电磁波传播环境通常会对无线通信产生重要的影响。针对不同的传输环境,提前分析收发位置之间的电波传播特性对建立无线传输系统有非常积极的作用。因此,建立高效且通用的电波传播分析算法就显得尤为重要。常见的电波传播算法有基于麦克斯韦方程组直接推导的全波数值分析算法、高频近似方法、抛物方程法和经验模型等。全波数值算法主要包括矩量法[1-2]、时域有限差分法(FDTD)[3-4]、有限元法(FEM)[5]等。全波数值算法通过严格的理论公式解析得出,具有非常准确的计算精度,但是当其应用到大范围电波传播问题分析时会遇到计算时间长、计算内存无法满足等问题;高频近似方法主要包含射线追踪法[6]、物理光学法[7]和等效电磁流法等,高频近似算法一般将实际辐射源近似为点源,具有计算速度快、对电脑内存需求小等优点,但是其在近似处理时会带近似误差;常见的电波传播经验模型有Okumura-Hata模型[8-10]和Longley-Rice模型[11-12]等,经验模型具有适用范围广泛且计算速度非常快的优点,但是其缺点也十分明显,其无法针对具体的电磁环境计算相对应的电波传播情况;抛物方程法被提出应用于大区域复杂环境中的电波传播预测[13],其在推导过程中对波动方程进行了近似处理,相较于传统全波算法,其省去了大量数值运算和矩阵运算,能极大提升求解效率并降低计算内存需求;相较于高频近似方法,抛物方程法只是在算法推导过程中做了近似处理,其计算误差小于高频近似法所带来的误差;相较于经验模型,抛物方程能针对具体的复杂电磁环境进行建模和仿真分析,这一点是经验模型所不能比拟的。
传统的抛物方程模型主要基于直角坐标系,其存在方位角计算受限制和计算效率较低等问题,不适用于全向天线的电波传播计算。1996年,Dockery首先提出了圆柱坐标系PEM的推导公式[14-15],但当时没有考虑电场沿方位角上的变化,这一点在后续的研究中才慢慢引入。圆柱坐标系PEM的推导基于柱坐标中的电场通解,然后将三角函数进行正交分解,最后将传统的抛物方程法延伸为柱坐标系PEM[16-17],求解方式为分布傅里叶变化(SSPE)。相较于传统的二维PEM,圆柱坐标系PEM能考虑真实的电波传播过程,将横向电磁波纳入了数值计算;相较于传统三维PEM,圆柱坐标系PEM计算时没有传播方位角的限制,能考虑类似基站天线等辐射全向电磁波的传播问题计算,具有更强的实用性。然而,传统的抛物方程和圆柱坐标系抛物方程均不适用辐射源的直接建模,并且在处理近源障碍物时,存在较大的误差。
针对辐射源周边存在障碍物条件下的电波传播问题,本文提出了MOM-PEM电波传播混合数值算法,在包含辐射源和近源障碍物的小区域内采用矩量法对电磁波进行建模和严格的解析计算,在MOM计算区域外的大区域内采用圆柱坐标系PEM进行电波传播数值近似计算。相比于传统的抛物方程法,该方法能对辐射源和近源障碍物直接进行建模,使电波传播仿真分析更贴近实际的同时还能减小误差;相比于全矩量法,该方法在辐射源和近源障碍物区域外的大场景采用PEM进行数值近似计算,可以大大提升仿真的计算效率。
1. MOM-PEM混合算法建模
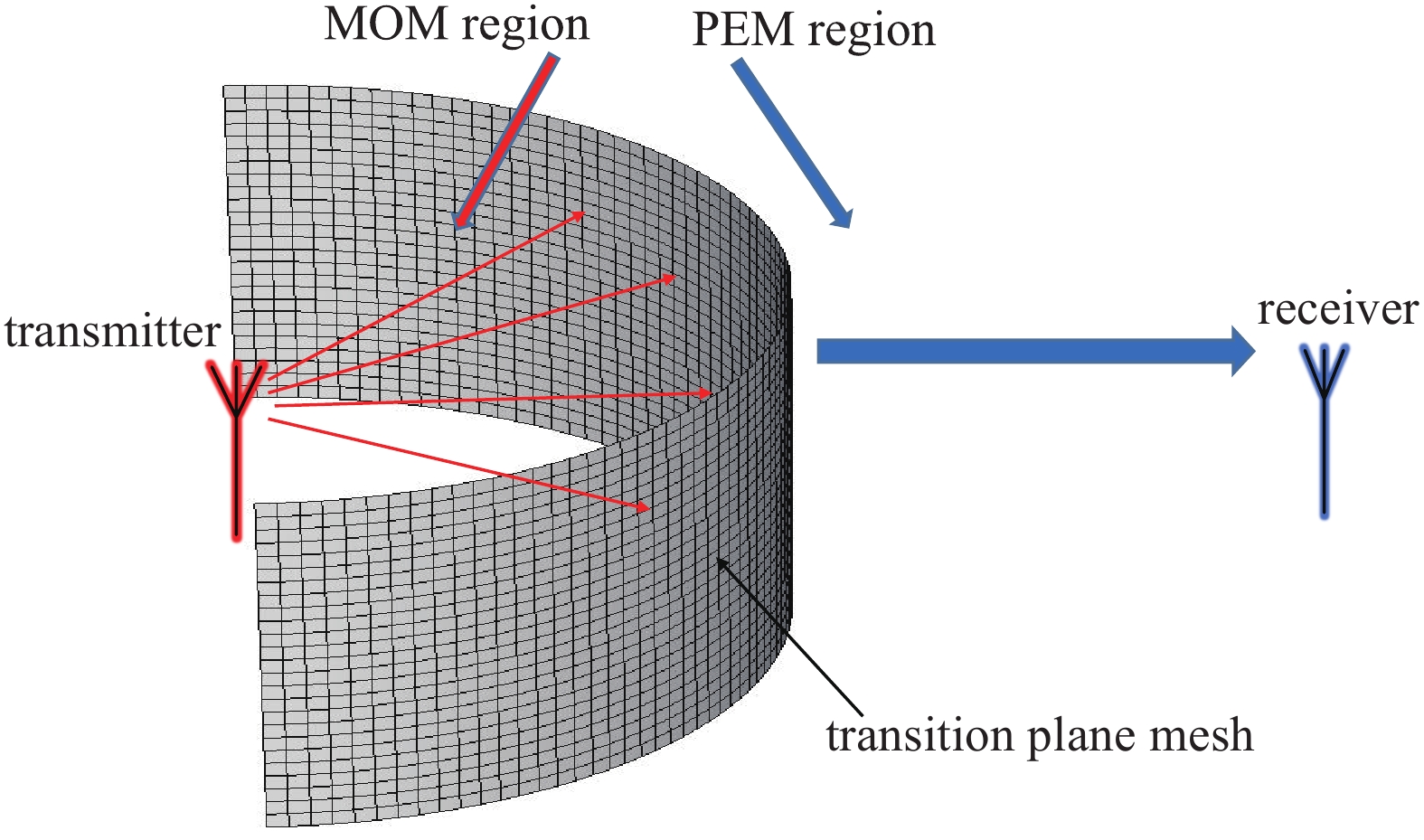
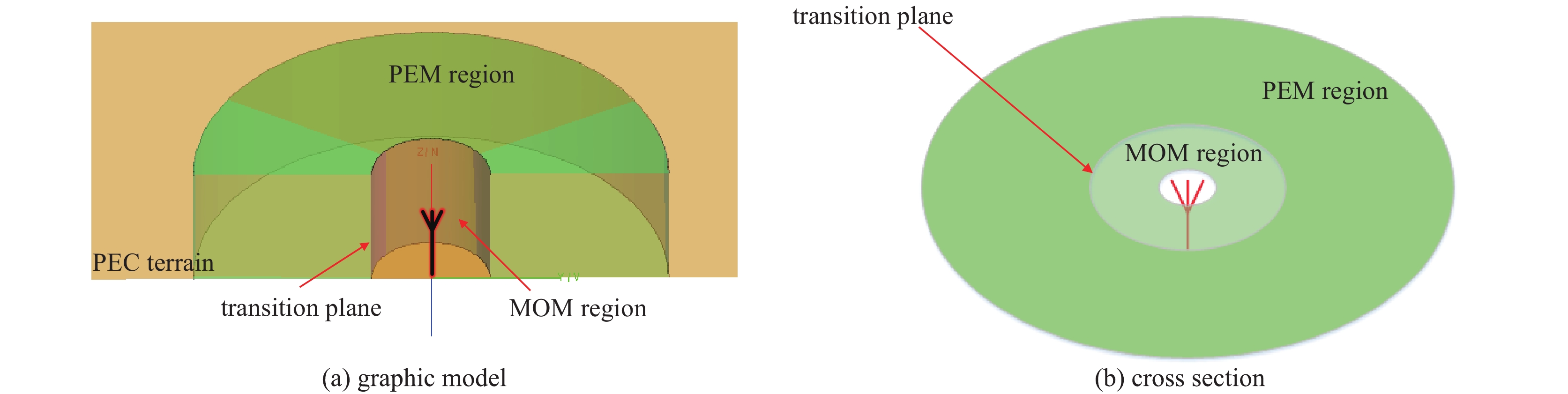
MOM-PEM混合算法的基本模型如图1所示。MOM计算区域为图1中的内圆柱区域,PEM计算区域为MOM计算区域外的大圆柱区域,两区域在垂直方向上的计算高度相同,区域之间的圆柱面为算法间进行场强数值传递的过渡面。
1.1 矩量法建模
矩量法计算区域内包含辐射源和近源障碍物。该区域内的地表面和障碍物按照RWG基函数进行电场积分方程的离散。区域内的辐射源模拟的为中心频率为2.4 GHz的半波偶极子天线,它在水平方向激励起的电磁波具有全向辐射性。区域内平坦地形采用的是PEC表面,这类理想表面本身也就是一种障碍物边界条件的模拟,对PEC地形进行网格剖分时,在满足求解精度的条件下对其进行了充分的三角形面元网格划分。
1.2 圆柱坐标系抛物方程法建模
本文所推导的抛物方程是考虑方位角变化的柱坐标系抛物方程。电场在沿高度方向传播时圆柱内部区域的行波叠加场满足贝塞尔函数J,电场沿径向传播时满足贝克尔函数H,将沿传播方向的外行波和内行波线性叠加后可以得到
R(r)=aJn(krr)|inner+bH(1)n(krr)|forward+cH(2)n|backward (1) 根据公式(1),可以得到柱坐标系PEM的迭代公式为
u(r,φ,z)=∑an,kzH(1)n(kr,r)ejnφejkzz (2) 式中:
n=jkφf,φ∈[0,2π] ,这里f为频率。由公式(2)可以得到圆柱坐标系PEM求解公式为(其中F为连续形式傅里叶变换)
u(r2,φ,z)=F(1)n,k2{H(1)n(krr2)/H(1)n(krr1)}F[u(r1,φ,z)] (3) 圆柱坐标系PEM计算区域内的地形也设置为PEC,这既是为了保持两类算法在计算区域过渡时的地形条件的一致也是为了计算的方便化处理。在柱坐标PEM计算区域内,圆柱面半径会随着计算区域的扩大越来越大,由此伴随的网格划分也会越来越稀疏,这就天然形成了PEM的非均匀网格而不需要单独去划分。在圆柱PEM计算区域的上方还需设置一个汉宁(Hanning)窗函数以吸收传播区域上方的反射波。
1.3 过渡区域
混合算法的过渡面如图2所示,图中只给出了半边区域的示意图。由于MOM和PEM都是基于频域的数值算法,两者之间的电场值传递可以通过网格点对数据进行采集和赋值而非常方便的完成。图中过渡面展示了PEM在方位角和高度上的离散网格数,其在10 m高度和360°方位角上的采集点数都为256。当MOM法计算到此过渡面时,会获得一个包含电场强度的
256×256 数据矩阵,这也就是圆柱坐标系PEM的初始场数据。2. 数值计算
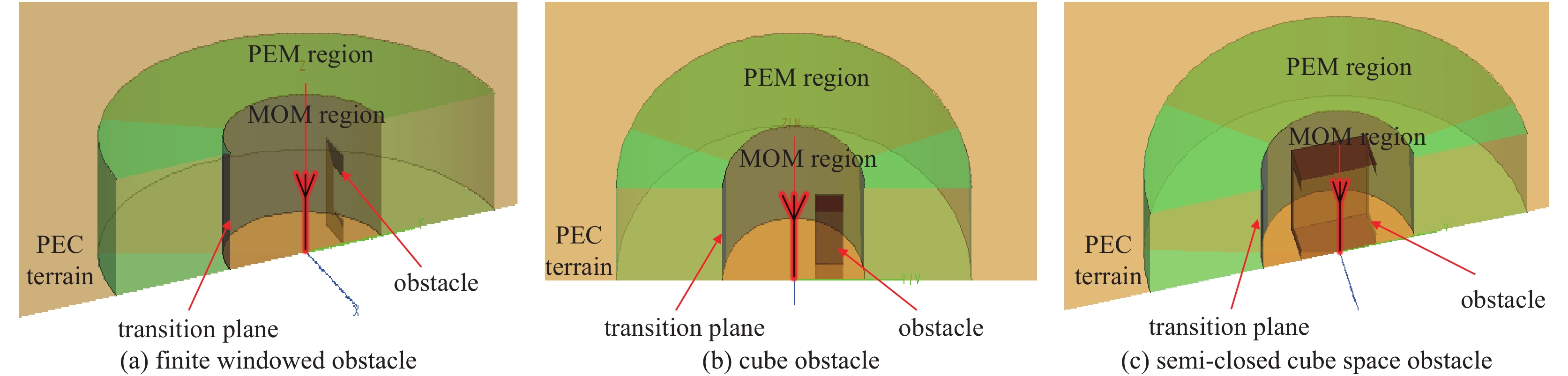
利用上述提出的混合算法计算三类不同近源障碍物存在条件下的电波传播问题,具体的截面示意图如图3所示。图3(a)中矩量法计算区域内存在一块有限开窗屏PEC障碍物;图3(b)中矩量法计算区域内存在一个立方体障碍物;图3(c)中矩量法计算区域内存在一两侧开窗的半封闭障碍物,发射天线位于半封闭障碍物之内,这样就能模拟半封闭空间内辐射源溢出的电磁波在外界的传播情况,此类场景类似于发射天线在室内,接收天线在室外的传播场景。
对于图3(a)所示的模型,MOM计算区域为半径
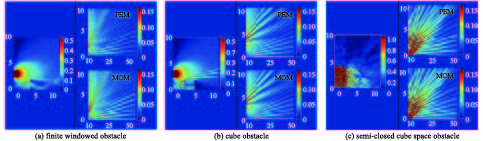
R1 =10 m,高度H1 =10 m的内圆柱区域;PEM计算范围为半径R2 =10~50 m,高度H2 =10 m的外圆柱区域;发射天线置于(0,0,3 m)处,中心频率为2.4 GHz;有限开窗屏置于(0,4 m,0)处,有限开窗屏沿x轴的长度L1 =5 m,沿z轴的长度L2=2 m;窗户的高度h=0.5 m,长L3 和宽W3 分别为3,1 m。图3(b)模型的计算区域、发射天线工作频率和图3(a)中相同,立方体障碍物与地面平齐的中心位置为(0,4 m,0),沿x,y,z轴的长/宽/高分别为3,2,2 m。图3(c)模型的计算区域、发射天线与图3其他模型一样,两侧开窗的半封闭立方体障碍物在平地面上的中心位置为(0,0,0),且其沿x,y,z轴的尺寸分别为4,8,4 m,开窗的长和宽都为3 m。PEM沿传播方向上的计算步长dx=0.25 m。图4中,黑色虚线左边为MOM计算结果,右边为PEM和 MOM计算结果,为了方便对混合算法计算结果和MOM计算结果进行对比,在绘图时将其拆分为两个部分:前10 m和后40 m的电场伪彩图;虚线右边上半区间10 m处的PEM初始场完全来自于虚线左边矩量法结尾处10 m的电场值。从图中还可以看出,在包含近源障碍物的MOM计算区域内,复杂障碍物产生的电波扰动现象得到了充分分析,障碍物的边界条件也得到了有效的处理,复杂障碍物和边界条件处理是MOM算法的优势同时也正是PEM的局限性所在。对于模拟的室内辐射源,由于半封闭空间对能量聚集的作用,辐射到空间中的电场值明显偏大。
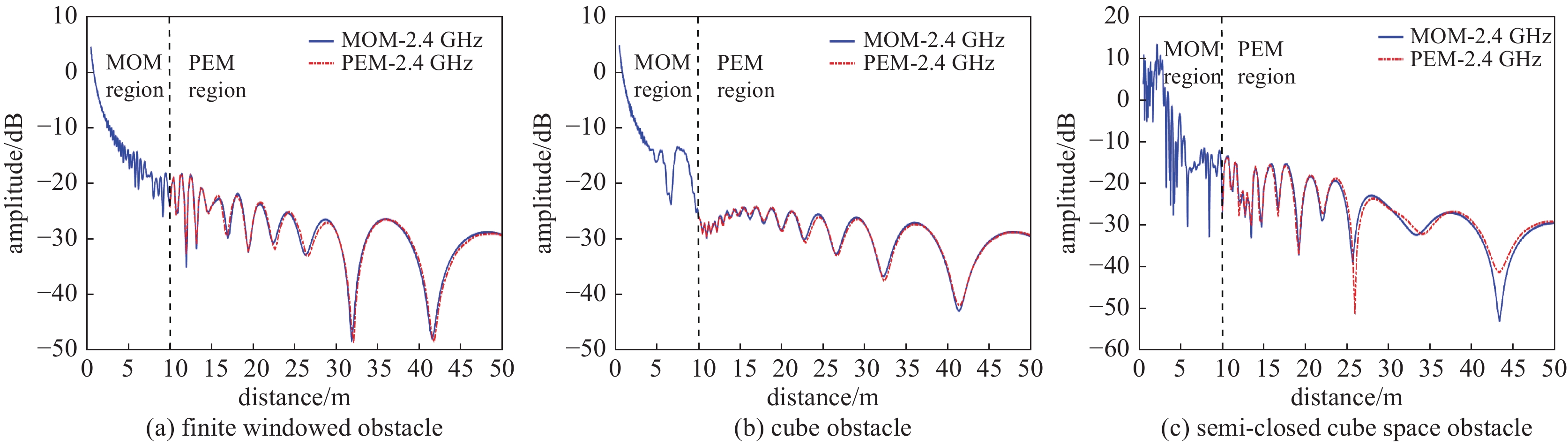
图5反映的是混合算法计算结果和全MOM数值计算结果在距离变化上的对比,电场采集点的接收高度为3 m。图中黑色虚线左边是MOM计算区域,虚线右边为PEM计算区域;从两者的对比图可以看出混合算法的计算结果和全MOM的计算结果吻合得很好;相较于整个计算区域都采用MOM进行数值计算,混合算法在后40 m采用的是计算速度较快的抛物方程算法,计算速率更快。如果是在更高的频率下,矩量法会对地表进行更小的网格划分,而抛物方程对步长的选取较为宽松,混合算法的计算优势将会得到进一步体现。
图4和图5展示的是电场随距离变化的对比。对于最远传播距离处电场随高度变化的数值计算结果将在图6给出。图6(a)为最远传播距离处电场随10 m高度变化的观察面效果图,即得到的是MOM-PEM混合算法在半径R=50 m,高度H=10 m的观察圆柱面上的电场值,图中红色越深代表场值越大,蓝色越深代表场值越小,混合算法计算结果和全矩量法计算结果的均方值误差值也体现在图上。图6(b)为具体的电场幅值随高度变化的数值计算结果,从结果可以看出,MOM计算区域内包含的近源障碍物越复杂,两者算法的误差也会有所增大,但是整体的趋势还是一致的,结果也吻合的较好。
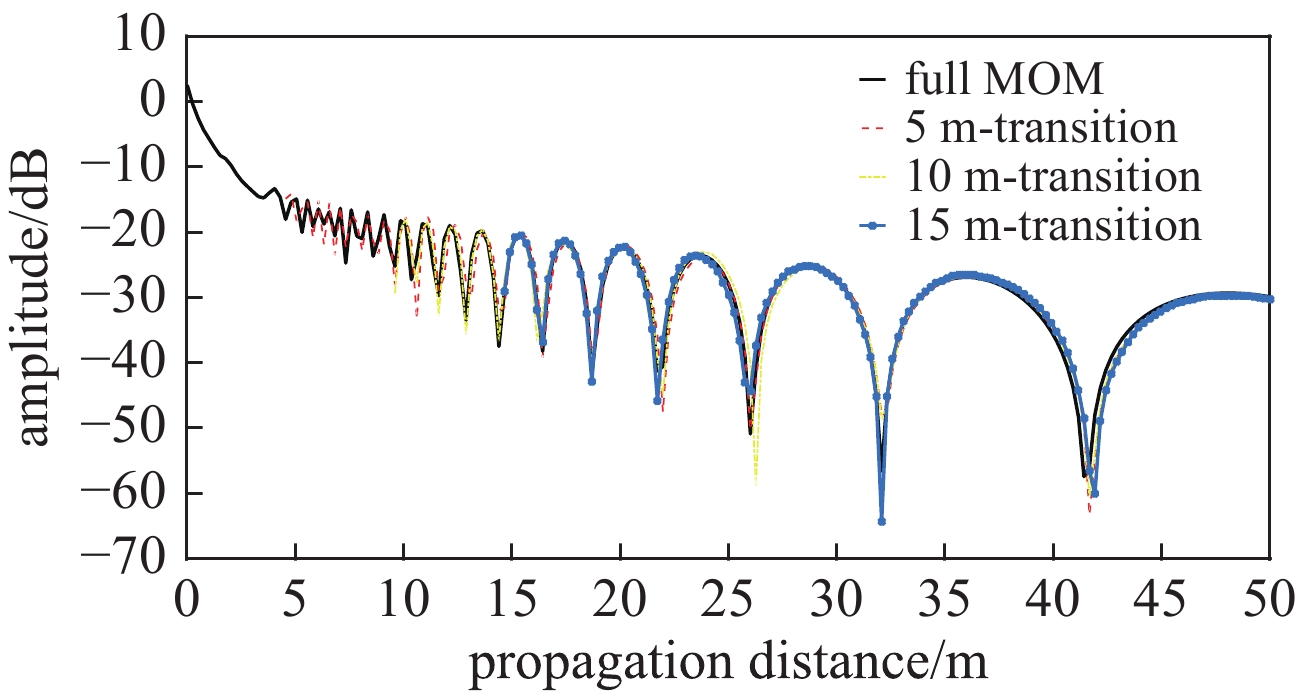
本文还针对MOM-PEM混合算法过渡面置于不同距离处对计算精度造成的影响展开了研究,结果如图7所示,此处计算时没有考虑障碍物存在的场景。从图中可以看出,将混合算法过渡面置于不同距离处对混合算法计算结果会产生一定的影响,但该影响都处于极小的误差范围之内,可以忽略不计。这验证了在MOM-PEM混合算法中,过渡面置于不同距离处不会影响MOM和PEM结合的精度。在实际应用中,可以在考虑计算机硬件条件的情况下根据近源障碍物尺寸灵活分配混合算法的计算区域,保证近源障碍物处于MOM计算区域即可。
3. 结 论
本文提出了一种新颖的MOM-PEM电波传播混合算法。在建模时,实际的全向辐射源在矩量法计算域中被模拟激励;不同形状的近源障碍物被建立并纳入仿真计算,在远场区采用柱坐标系PEM进行电波传播数值仿真。针对近源区域包含有限开窗屏障碍物、立方体障碍物以及半封闭空间障碍物的三种典型场景进行了仿真计算,并将混合算法的计算结果和采用全矩量法计算得到的结果进行了数据对比,结果表明混合算法具精度的同时且更具实用性。本文所提出的混合算法特别适用于发射天线周边存在复杂地形或者障碍物,同时又需要进行大范围电波传播研究的综合问题分析。
-
[1] Johnson J T, Shin J C, Edison J C, et al. A method of moments model for VHF propagation[J]. IEEE Trans Antennas and Propagation, 1997, 45(1): 115-125. doi: 10.1109/8.554248 [2] Akleman F, Sevgil. A novel MoM- and SSPE-based groundwave-propagation field-strength prediction simulator[J]. IEEE Antennas and Propagation Magazine, 2007, 49(5): 69-82. doi: 10.1109/MAP.2007.4395296 [3] Yee K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media[J]. IEEE Trans Antennas and Propagation, 1996, 14(3): 302-307. [4] Akleman F, Sevgil. A novel implementation of Berenger’s PML for FDTD applications[J]. IEEE Microwave and Guided Wave Letters, 1998, 8(10): 324-326. doi: 10.1109/75.735409 [5] Pichon L. Finite element analysis of bounded and unbounded electromagnetic wave problems[C]//IEE Colloquium on High Frequency Electromagnetic Modelling Techniques. 1995: 1/1-1/3. [6] Grubisic S, Carpes W P, Lima C B, et al. Ray-tracing propagation model using image theory with a new accurate approximation for transmitted rays through walls[J]. IEEE Trans Magnetics, 2006, 42(4): 835-838. doi: 10.1109/TMAG.2006.871673 [7] 朱艳菊, 江月松, 辛灿伟, 等. 应用改进的物理光学法和图形计算电磁学近似算法快速计算导体目标电磁散射特性[J]. 物理学报, 2014, 63(16):182-188. (Zhu Yanju, Jiang Yuesong, Xin Canwei, et al. Fast computation of electromagnetic scattering characteristics from conducting targets using modified-physical optics and graphical electromagnetic computing[J]. Acta Physica Sinica, 2014, 63(16): 182-188 [8] Medeisis A, Kajackas A. On the use of universal Okumura-Hata Propagation prediction model in rural areas[C]//IEEE 51st Vehicular Technology Conference Proceeding. 2000, 3: 1815-1818. [9] Alamoud M A, Schutz W. Okumura-Hata model tuning for TETRA mobile radio networks in Saudi Arabia[C]//2nd International Conference on Advances in Computational Tools for Engineering Application. 2012: 47-51. [10] Capizzi G, Coco S, Laudani A, et al. A new tool for the identification and localization of electromagnetic sources by using independent component analysis[J]. IEEE Trans Magnetics, 2007, 43(4): 1625-1628. doi: 10.1109/TMAG.2006.892251 [11] Weiner M. Use of the Longley-Rice and Johnson-Gierhart tropospheric radio propagation programs: 0.02-20 GHz[J]. IEEE Journal on Selected Areas in Communications, 1986, 4(2): 297-307. doi: 10.1109/JSAC.1986.1146313 [12] Zuliang W, Mao Z, Juan W, et al. Improved algorithm of atmospheric refraction error in Longley-Rice channel model[J]. Journal of Systems Engineering and Electronics, 2008, 19(4): 683-687. doi: 10.1016/S1004-4132(08)60139-5 [13] Leontovich M A, Fock V A. Solution of the problem of propagation of electromagnetic waves along the Earth’s surface by method of parabolic equation[J]. Journal of Physics of the USSR, 1946, 10(1): 13-24. [14] Dockery G D. Modeling electromagnetic wave propagation in the troposphere using the parabolic equation[J]. IEEE Trans Antennas and Propagation, 1988, 36(10): 1464-1470. doi: 10.1109/8.8634 [15] Dockery D, Kuttler J R. An improved impedance-boundary algorithm for Fourier split-step solutions of the parabolic wave equation[J]. IEEE Trans Antennas and Propagation, 1996, 44(12): 1592-1599. doi: 10.1109/8.546245 [16] 胡绘斌. 预测复杂环境下电波传播特性的算法研究[D]. 长沙: 国防科学技术大学, 2006.Hu Huibing. Study on the algorithms of predicting the radio propagation characteristics in complex environments[D]. Changsha: National University of Defense Technology, 2006 [17] 周亮. 大区域复杂地理环境的交替方向分解抛物方程电波传播模型及其应用研究[D]. 成都: 西南交通大学, 2018.Zhou Liang. Study on the ADD-PE method and its applications for radio propagation problems in large geometric environment[D]. Chengdu: Southwest Jiaotong University, 2018 -






 下载:
下载:


















 下载:
下载: