Conjugate rotation smoothing scheme for laser quad based on dual-frequency laser and spiral phase plate
-
摘要: 提出了一种基于双频光源和涡旋相位板实现光束快速互补旋转的集束匀滑方案。双频光源为集束中各子束提供频移,拓扑荷数相同但反号的涡旋相位板阵列用于将各个子束变换成拉盖尔—高斯(LG)光束,而通过偏振控制则可实现子束间两两的相干叠加。在此基础上,通过采用共轭连续相位板可使波长不同、偏振态不同的子束组合在靶面形成快速旋转且空间上互补填充的焦斑。结果表明,利用这一方案可实现子束散斑在靶面上快速旋转且散斑分布保持互补,进而有效改善靶面辐照均匀性,甚至为抑制激光等离子体不稳定性提供了一种潜在途径。
-
关键词:
- 惯性约束聚变 /
- 集束匀滑 /
- 涡旋相位 /
- 辐照均匀性 /
- 激光等离子体不稳定性
Abstract: Conjugate rotation smoothing scheme for laser quad based on dual-frequency laser and spiral phase plate was proposed. The dual-frequency laser provides frequency shift among the beamlets, the spiral phase plates with same helical charge but opposite sign transform the beamlets into Laguerre-Gaussian beams, and the polarization control is applied to make these beamlets coherently superposed on the target plane. On this basis, the conjugate continuous phase plates are adopted to enable the beamlets with different central wavelength and orthogonal polarization form focal spots with rapid rotation. Moreover, the spatiotemporal focal spot of the laser quad looks like conjugate spin light because of the frequency beats. It is indicated that, the scheme enables the fine-scale speckles within the focal spot rotate in a period of a few picoseconds, and even exhibit different intensities and wavelengths at different time and different positions. Hence, the novel scheme can effectively smooth the irradiation uniformity of the laser quad and even has the potential to mitigate laser plasma interactions. -
在激光驱动的惯性约束聚变(ICF)装置中,光束匀滑技术是抑制流体力学不稳定性和激光等离子体不稳定性(LPI)的重要手段之一[1]。美国国家点火装置(NIF)[2]的实验结果表明,光束匀滑技术是影响点火成败的关键因素。目前,主流的光束匀滑技术分为三类:用于焦斑空间包络整形的连续相位板(CPP)[3],时域匀滑以抑制散斑的光谱角色散匀滑(SSD) [4]和使光束非相干叠加以实现瞬时匀滑的偏振匀滑(PS)[5]。其中,CPP用于控制焦斑大尺度包络,但会由于子波面间的干涉产生小尺度散斑,而SSD和PS则侧重于抑制散斑。SSD的核心思想是通过电光相位调制器(EOM)[6]和光栅引入光束的动态波前倾斜,导致散斑在靶面沿光栅色散方向扫动,从而抹平不均匀性。受限于EOM的调制频率,散斑的扫动周期约为数十ps,因而焦斑达到稳定均匀性也往往需要数十ps。然而,这一周期远远长于LPI增长的特征时间,比如受激拉曼散射(SRS)、受激布里渊散射(SBS)和交叉光束能量转移[7-9],导致SSD对LPI的抑制效果不佳[10]。因此,亟需发展新型超快速匀滑技术,以在进一步改善靶面辐照均匀性的前提下,实现散斑在靶面上皮秒时间尺度运动。
近年来,涡旋光束[11]因其轨道角动量特性而在光学成像[12]、显微操控[13]和自由空间光通信[14]等方面得到了飞速发展。已有研究表明,两束携带相反拓扑荷数且具有频移的涡旋光束在相干叠加后,拍频效应会导致合成光束的光强分布快速旋转,且旋转频率与频移量相当[15]。值得指出的是,这一光强分布的快速旋转与SSD导致的散斑扫动是类似的,不仅可用于改善光束的辐照均匀性,甚至在破坏LPI的增长方面存在潜在应用。
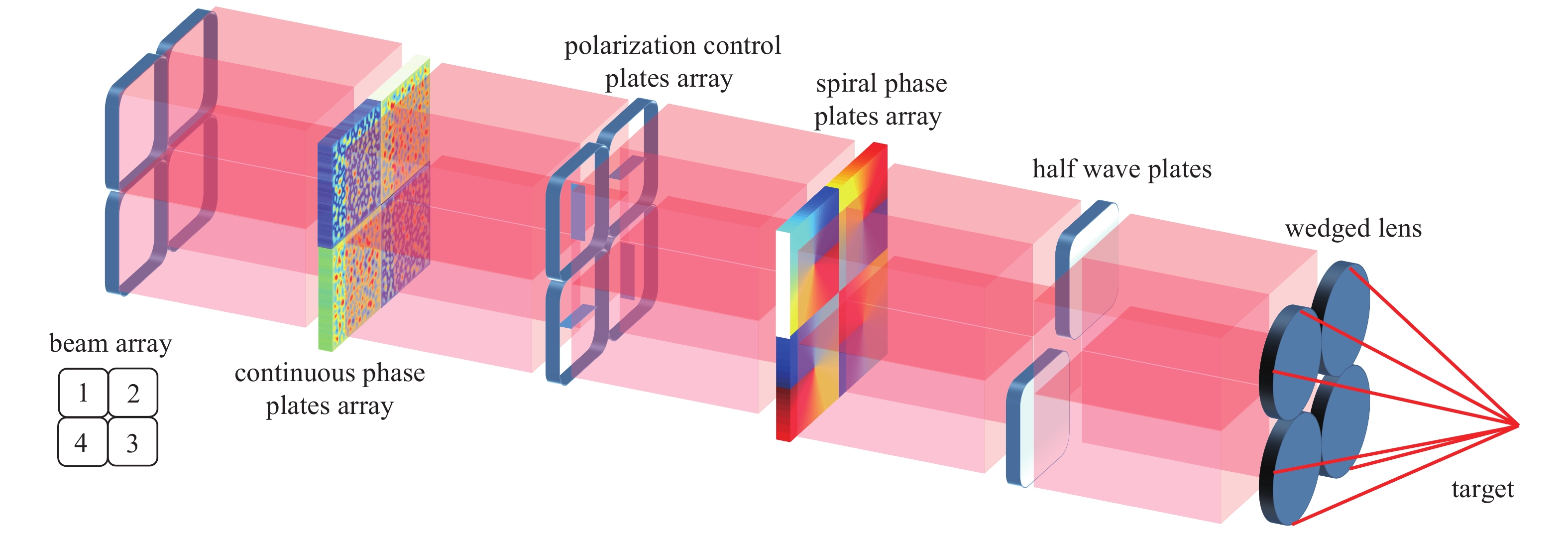
本文提出一种基于双频光源和涡旋相位板以实现光束快速互补旋转的集束匀滑方案。采用双频光源注入以使集束中相邻两子束存在中心频移,而通过偏振控制实现子光束间两两的相干叠加。然后,利用拓扑荷数相同但反号的涡旋相位板(SPP)阵列对各个子束进行光束变换,并采用共轭连续相位板(CPP)对子束进行空间相位整形。因此,当偏振态相同、拓扑荷数反号的两子束在靶面相干叠加时,焦斑光强由于拍频效应而产生快速旋转。在此基础上,通过在其中两个子束加入半波片,就可以使两两子束相干叠加的焦斑在空间上互补填充,从而达到整体匀滑的效果。
1. 互补旋转集束匀滑方案
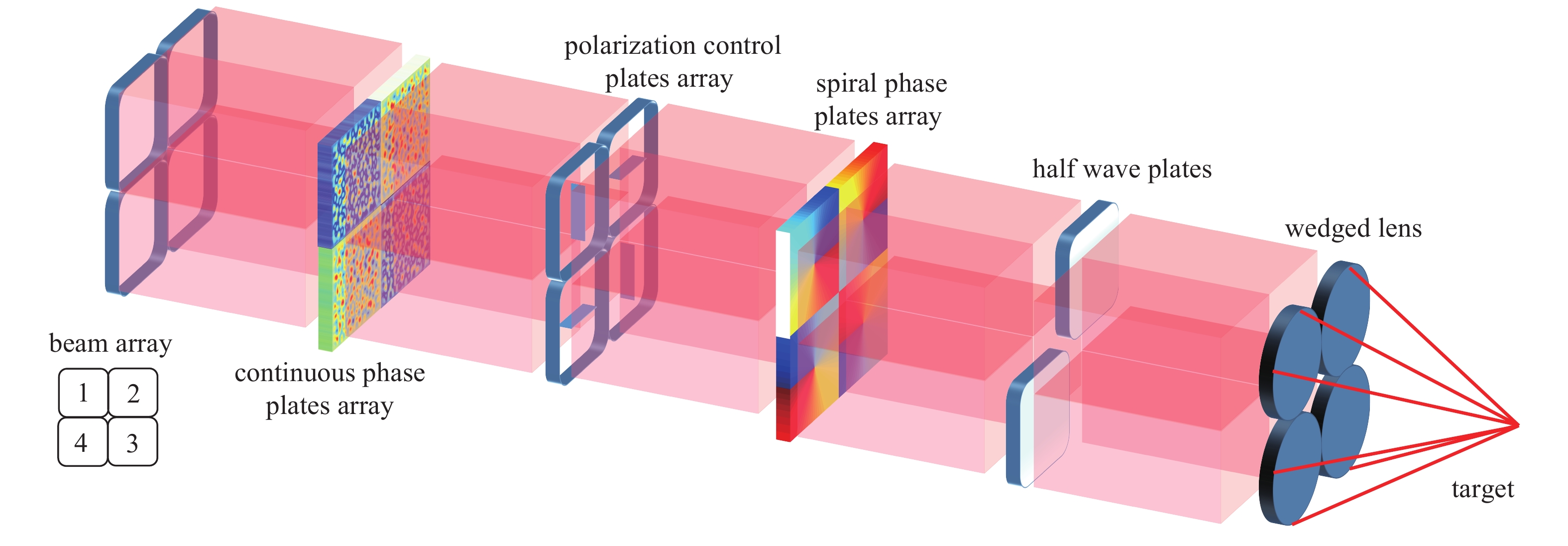
在诸如NIF这样的高功率激光装置中,激光束以2×2集束的方式进行空间排布,每一子束单独经过预放大、主放大和倍频等过程,最后经楔形透镜聚焦在靶面上。图1给出了互补旋转集束匀滑方案的示意图,子束1,3和2,4分别经过相同的CPP,SPP和偏振调控单元,但子束1,3和2,4经过的CPP面形共轭,SPP的拓扑荷数相同但反号。此外,在子束2和4中单独插入半波片,以使子束1,3的焦斑分布与子束2,4的焦斑分布在靶面互补填充。
在图1中,子束1,3的传输叠加特性与子束2,4相同,因而我们以子束1,3为例,建立了光传输模型并给出靶面光场解析表达式。为便于讨论而不失一般性,我们先忽略CPP的空间位相整形效果,得到子束1,3在透镜前的光场分布为
Enj(r,t)=ex(rσ)|l|exp(−r2σ2)exp(ilθ+iωjt) (1) 式中:
ex 为偏振单位矢量;r=(x2+y2)1/2;σ为束宽;l为拓扑荷数;θ=arg(x+iy)为方位角;ωj(j=1,3)是子束1,3的中心角频率。利用衍射积分方法,可得到远场光场表达式为
Efj(x,y,t)=−exexp(ikjf)iλjf∬(rσ)|l|exp(−r2σ2)exp(ilθ+iωjt)[−ikj2f(xxf+yyf)]dxdy (2) 式中:kj=2π/λj(j=1,3)为子束1,3波数;λj(j=1,3)为中心波长;f为焦距。(x,y)和(xf,yf)为近场和远场空间坐标。
利用欧拉公式,可将公式(2)简化为
Ej(r,t)=ex(rσ)|l|exp(−r2σ2)exp(ilφ+iωjt)=ex(rσ)|l|(cosφ+isinφ)lexp(−r2σ2)exp(iωjt)=ex(x+iyσ)lexp(−r2σ2)exp(iωt) (3) 进一步式将式(3)代入式(2),令
u=x+ikσ2xf2f,v=y+ikσ2yf2f ,则公式(2)可写为Efj(x,y,t)=exexp(ikjf)iλjfexp(iωjt)exp(−k2σ2(x2f+y2f4f2))×∬[u+iv+ikσ22z(yf−ixf)σ]lexp(−u2+v2σ2)dudv (4) 在公式(4)中,
(u+iv)exp(−u2+v2σ2) 是积分为0的奇函数,因而可进一步简化为Efj(x,y,t)=exexp(ikjf)iλjfexp(iωjt)exp(−k2σ2(x2f+y2f4f2))×∬[ikσ22z(yf−ixf)σ]lexp(−u2+v2σ2)dudv=exexp(ikjf)iλjfexp(iωjt)exp(−k2σ2(x2f+y2f4f2))[ikσ22z(yf−ixf)σ]×∬exp(−u2+v2σ2)dudv=exexp(ikjf)iλjfexp(iωjt)exp(−k2σ2(x2f+y2f4f2))[ikσ22z(yf−ixf)σ]×πσ2 (5) 根据欧拉公式有
yf−ixf=−i(reiφf) ,可进一步将式(5)式简化为Ef(xf,yf,t)=ex(−i)l(rfπσ3kexp(ikf)2λf2)exp(−rf24f/k2σ2)exp(ilφf+iωjt) (6) 忽略子束1,3波矢的差异,则远场光强可简化为
If(x,y,t)=|exEf1+exEf3|2=[(rfπσ3k12λf2)exp(−rf24f/k12σ2)]2{2+2cos[2θ+(ω1−ω3)t]} (7) 公式(7)表明,焦斑的光强分布会产生快速旋转,且其旋转周期取决于子束间频移量。类似地,子束2,4的焦斑光强分布也可以用公式(7)表示,但由于半波片的作用,其初始光强分布与1,3焦斑光强分布存在初始错位。于是,子束2,4的光强分布可表示为
I′f(x,y,t)=|eyEf2+eyEf4|2=[(rfπσ3k22λf2)exp(−rf24f/k22σ2)]2{2+2cos[2θ+(ω2−ω4)t+π]} (8) 比较公式(7)和公式(8)可以看出,子束2,4的光强分布与子束1,3的光强分布存在初始空间相位差,因而两者在空间上互补填充,且其旋转周期一致。激光集束光强分布则为两者的非相干叠加,即
Isum(x,y,t)=If(x,y,t)+I′f(x,y,t)=[(rfπσ3k12λf2)exp(−rf24f/k12σ2)]2{2+2cos[2θ+(ω1−ω3)t]}+[(rfπσ3k22λf2)exp(−rf24f/k22σ2)]2{2+2cos[2θ+(ω2−ω4)t+π]} (9) 当仅考虑焦斑的时间特性时,由公式(9)可知其旋转周期为T=lλ2/cΔλ。进一步地,我们考虑CPP的空间位相整形作用,则焦斑的光强分布表示为
I′sum(x,y,t)=If(x,y,t)⊗FT[exp(iΦCPP)]+I′f(x,y,t)⊗FT[exp(i(2π−ΦCPP))] (10) 式中:FT表示傅里叶变换;
⊗ 为卷积;ΦCPP为CPP的附加空间位相。从公式(5)和(6)可以看出,激光集束的焦斑光强分布同时受频移量和拓扑荷数影响。互补旋转集束匀滑方案存在两大特征:(1)由于拍频效应,子束1,3和2,4的焦斑均以频移量为旋转频率快速旋转,而通过调节频移量就能够使旋转周期为数ps;(2)子束1,3和2,4的焦斑在旋转过程中保持在空间上互补填充。
2. 束匀滑特性分析
基于上述建立的物理模型,我们首先分析集束焦斑光强的旋转特性。然后,针对互补旋转集束匀滑方案的束匀滑特性展开讨论,分析关键参数(频移量/波长差、振幅调制和位相调制等)的影响及规律。最后,将这一新方案与径向匀滑方案(RS)[16]进行联用。
2.1 光强旋转特性
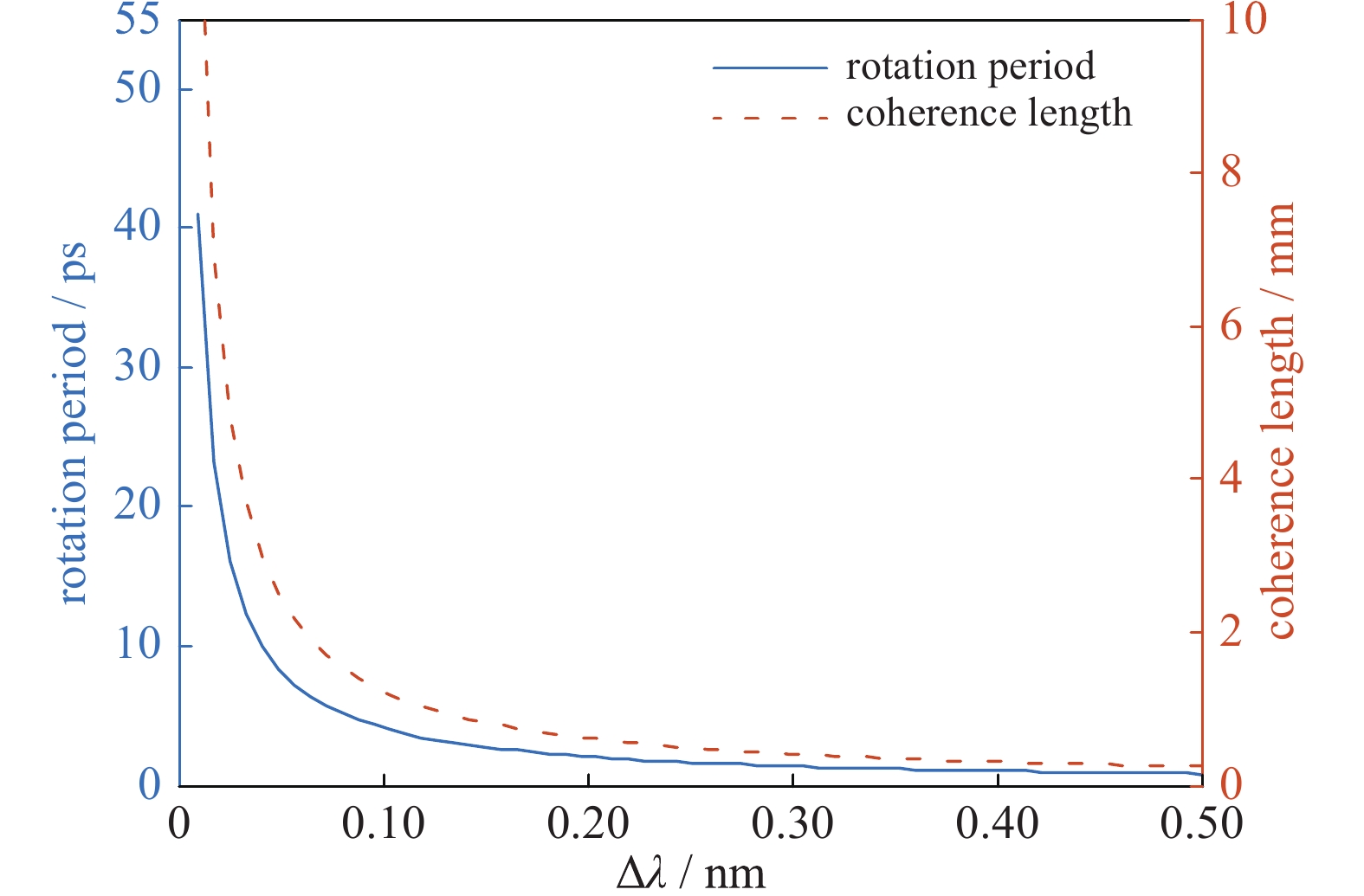
为更好地突显集束光强的旋转特性,我们在忽略CPP空间位相整形效果的前提下,给出了集束焦斑的光强分布,如图2所示。所用计算参数为:SPP的拓扑荷数为l=±1,波长差为0.3 nm。为简便起见,子束1~4的中心波长分别为λ1,2=351.0 nm,λ3,4=351.2 nm。各子束的光束口径为360 mm×360 mm,透镜焦距为7.7 m。
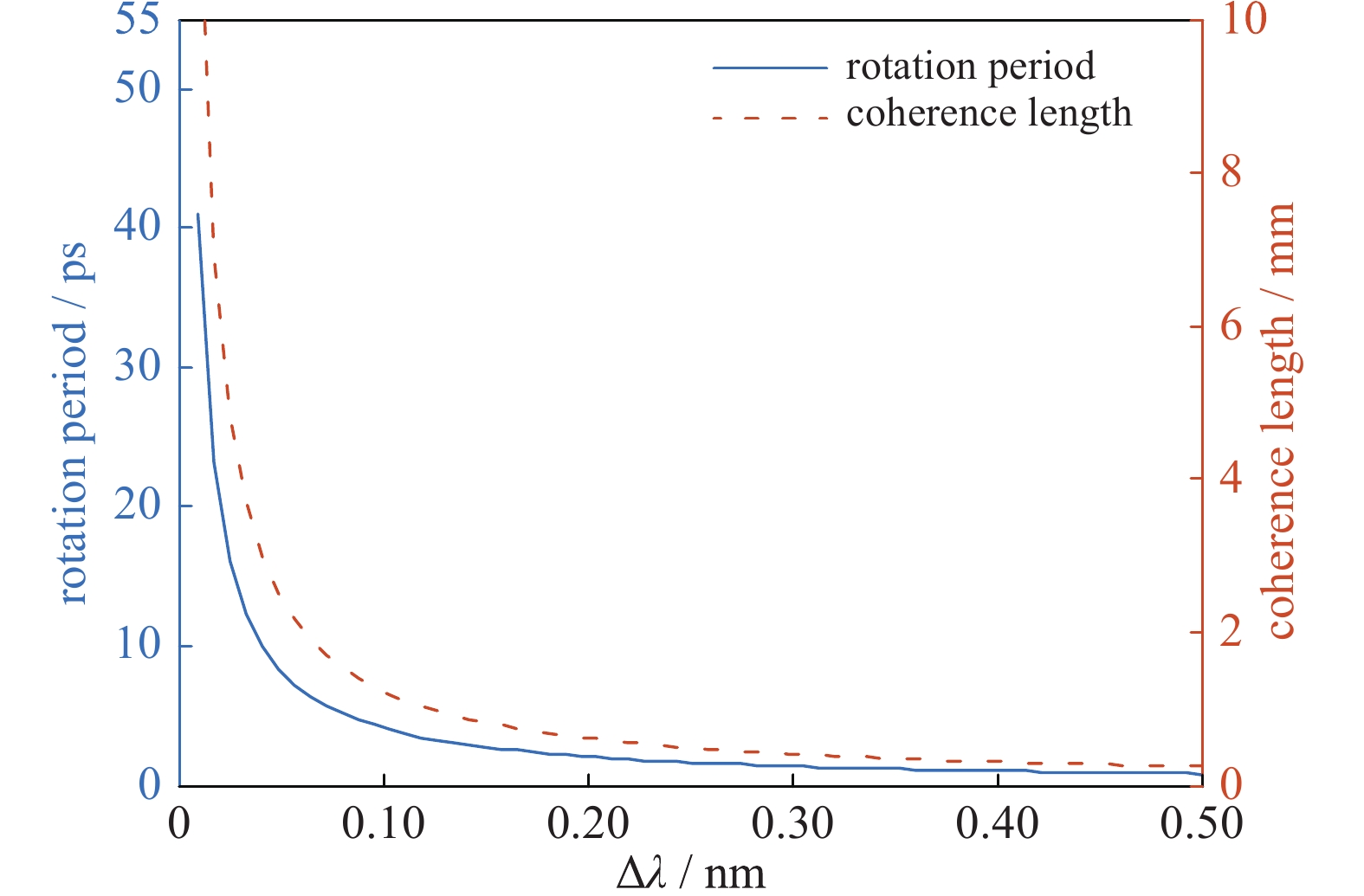
从图2可以看出,当SPP拓扑荷数为l=±1时,焦斑光强分布分为四个旋转的“扇叶”,每个“扇叶”的大小和光强分布一致,并以相同周期快速旋转。如果进一步考虑CPP对焦斑包络的控制效果,则焦斑光强包络会产生快速旋转,并致使其内部散斑在角向上快速再分布,从而达到提高辐照均匀性的目的。由于散斑重新分布周期可短于LPI的增长特征时间,因而这一方案在破坏LPI增长存在潜在应用。例如,当中心波长为351 nm而波长差为0.2 nm时,旋转周期约为2 ps,短于SRS增长特征时间。此外,通过合理选择波长差和拓扑荷数,子束间的空间相干长度能长于集束在柱型靶腔内的传输距离,从而使集束焦斑在一个相对长的距离内保持旋转,如图3所示。
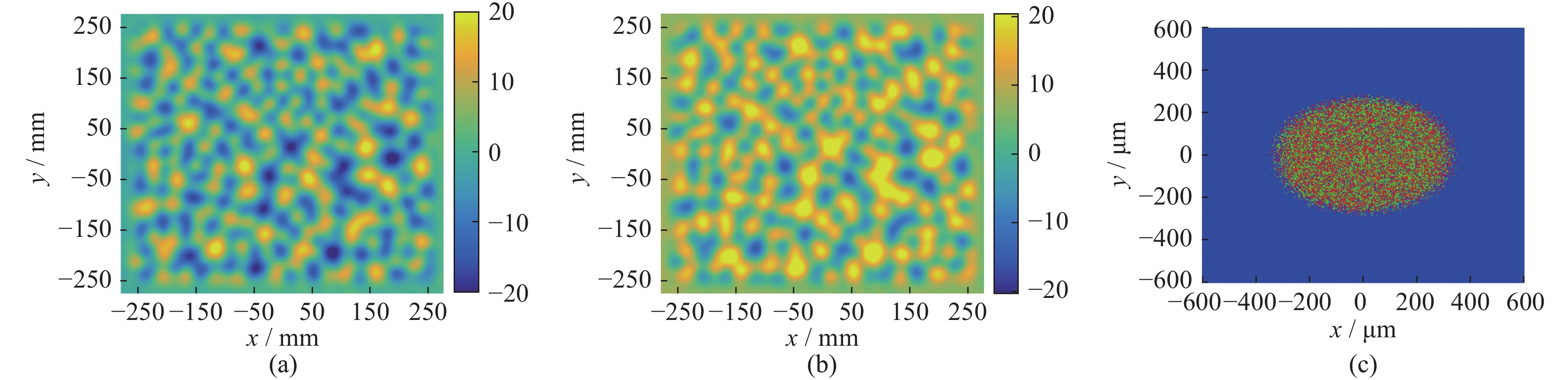
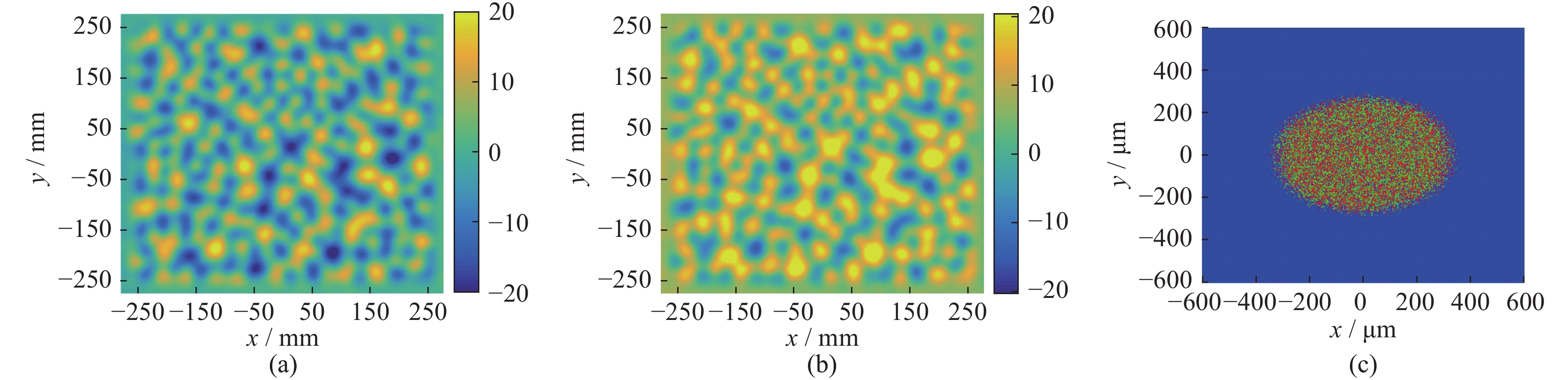
我们进一步分析由CPP产生的散斑如何在空间上互补填充。CPP在控制焦斑包络时,不可避免地会由于子波面间的干涉而产生散斑。我们针对面形共轭CPP的研究表明,共轭CPP所产生的焦斑光强分布在一定程度上是互补的。图4(a)和(b)分别给出了一组面形共轭的CPP,图4(c)则给出同一光束分别经原CPP和共轭CPP的焦斑光强分布,其中,红色区域表示经原CPP的焦斑,绿色区域表示经共轭CPP的焦斑。
 图 4 (a)原CPP和(b)共轭CPP的面型分布,(c)两光束分别经共轭CPP的焦斑光强分布Figure 4. Surface shape of an original CPP (a) and its conjugate CPP (b). (c) is the far-field intensity distributions of a same laser beam after propagating through these two CPPs. Red regions shows the speckles generated by the original CPP, and green regions within the focal spot show the speckles generated by the conjugate CPP
图 4 (a)原CPP和(b)共轭CPP的面型分布,(c)两光束分别经共轭CPP的焦斑光强分布Figure 4. Surface shape of an original CPP (a) and its conjugate CPP (b). (c) is the far-field intensity distributions of a same laser beam after propagating through these two CPPs. Red regions shows the speckles generated by the original CPP, and green regions within the focal spot show the speckles generated by the conjugate CPP从图4(c)可以看出,原CPP与共轭CPP产生的焦斑包络一致,且二者焦斑的散斑在空间上大致互补填充,即原CPP产生的热斑位于共轭CPP产生的非热斑位置。值得指出的是,可以进一步通过优化CPP设计而增强这一空间互补效果。因此,如果进一步将散斑空间互补与焦斑快速旋转相结合,则可以使散斑在保持空间互补的前提下以同一周期旋转,从而更有效地改善靶面辐照均匀性。如果进一步使两空间互补的焦斑的中心波长有所差异,则对于靶面上某一位置而言,其光强和波长均会产生快速变化,这将有利于破坏非线性效应的波矢匹配条件,从而达到抑制LPI增长的效果。例如,当子束1,3和子束2,4的中心波长差均为0.5 nm,而其中心波长分别为λ1=351.00 nm,λ2=350.80 nm,λ3=351.10 nm,λ4=351.30 nm时,焦斑光强的旋转周期一致但中心波长差异较大,因而对LPI具有潜在的抑制效果。
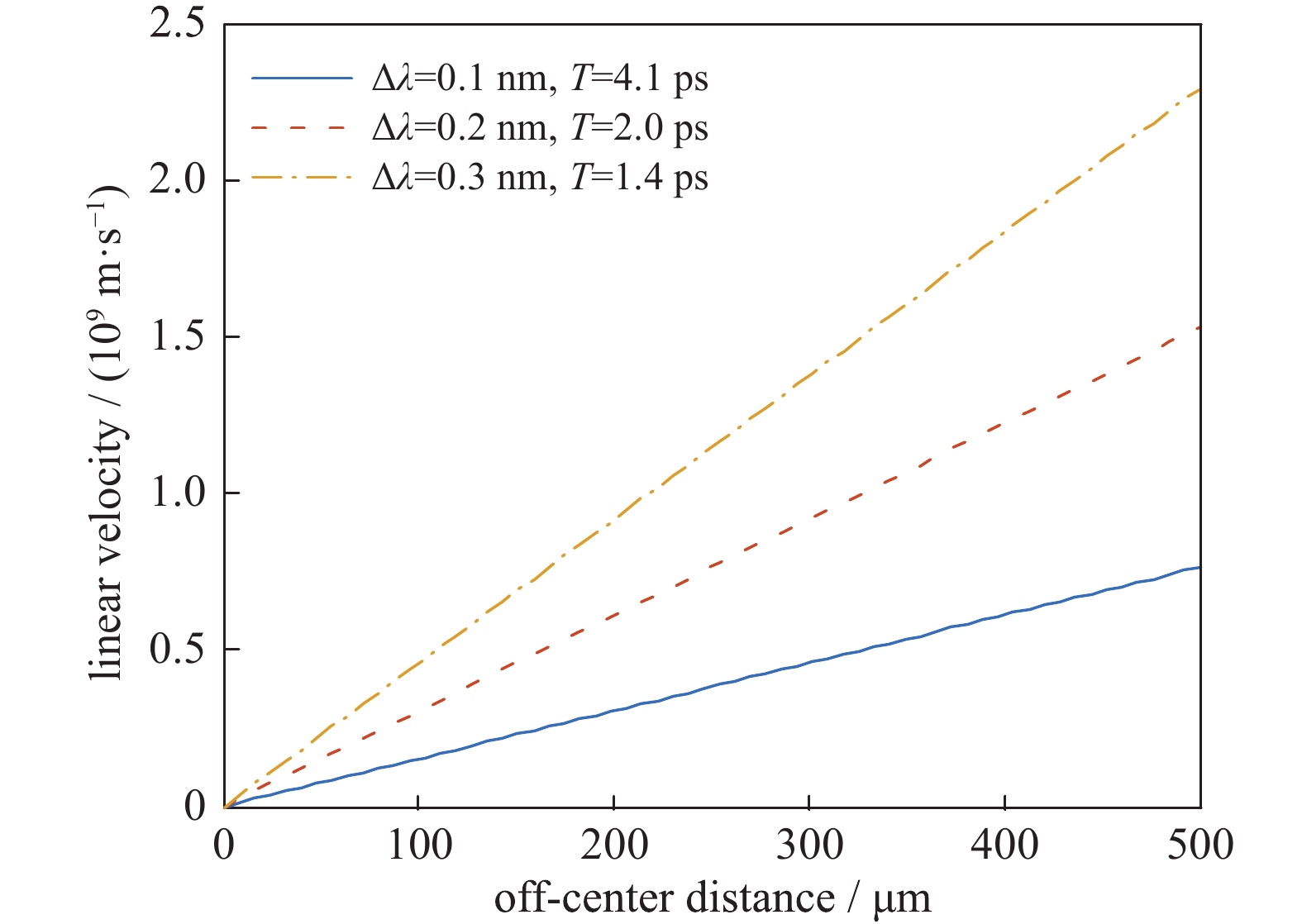
如图3和图4(c)所示,焦斑的旋转周期为T=lλ2/cΔλ,而内部散斑的线速度取决于焦斑半径,即其旋转线速度为v=2πrcΔλ/lλ2。
图5给出了散斑线速度随着偏离中心距离的变化规律。可以看出,内部散斑的角速度相同,但线速度随着焦斑半径的增大而线性增大。进一步分析图5可知,散斑的线速度可达2×109 m/s(或2×103 μm/ps),意味着散斑的重新分布速度甚至可超光速。这是由于散斑的旋转是由于相干光束的涡旋相位产生的,相当于是焦斑能量在角向方向的重新分布而不是光束能量的传播,实际上体现的是光束传输的相速度。此外,相比于传统SSD方案中导致的焦斑横向扫动,这一方案仅产生焦斑的旋转,不会增大焦斑尺寸,因而在避免“堵孔”效应上更具有优势。
需要指出的是,焦斑的旋转不会引起中心散斑的扫动,因而中心散斑的强度会随着积分时间的增长而持续提高,导致最终的焦斑均匀性不足。因此,互补旋转集束匀滑方案还需要与其它匀滑方案进行联用,以产生联动效果。
2.2 束匀滑效果
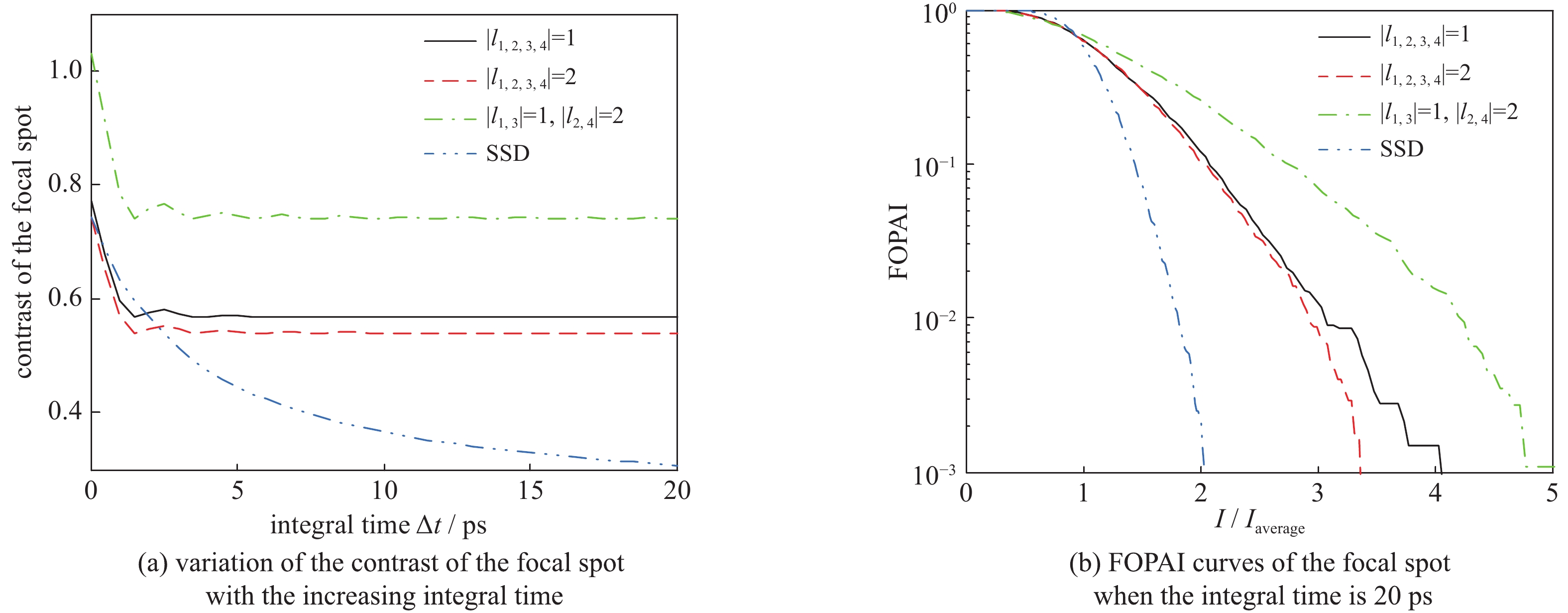
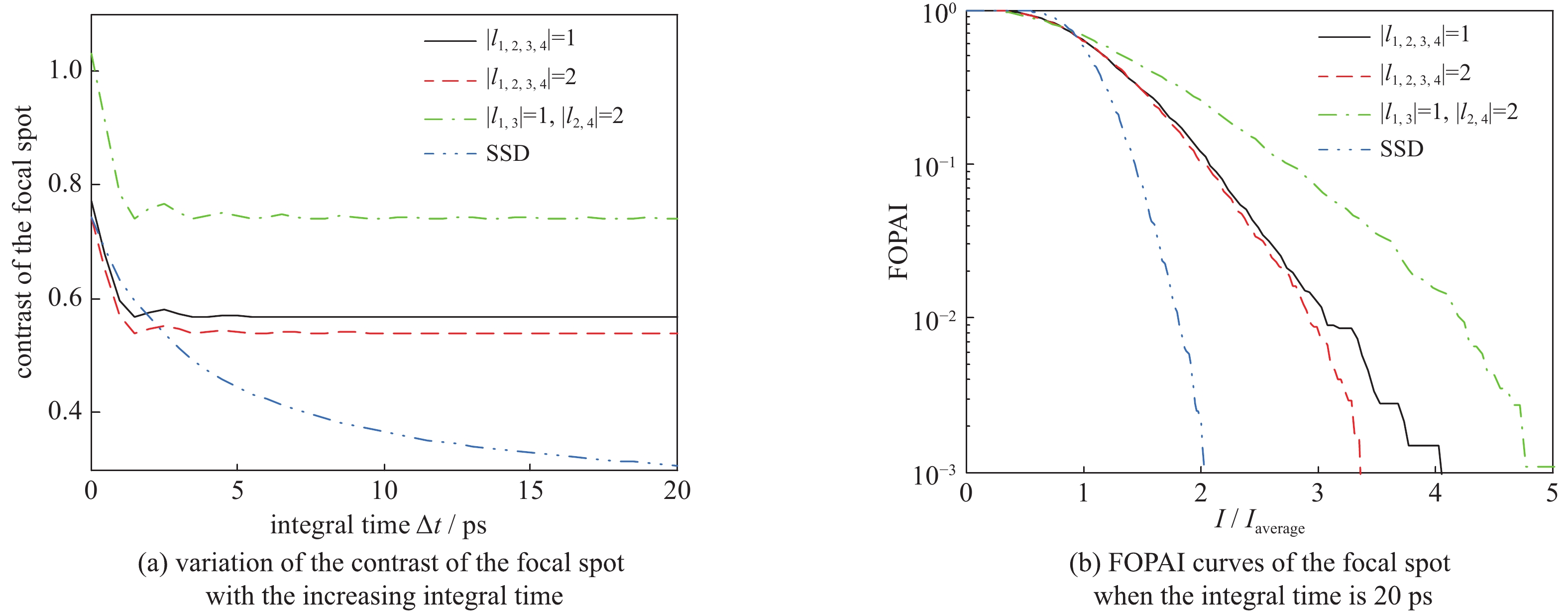
在互补旋转集束匀滑方案中,焦斑包络的扫动可以使其内部散斑重新分布,从而提高靶面辐照均匀性。图6(a)中给出了激光集束焦斑的光通量对比度随积分时间的变化,图6(b)中则给出相应的FOPAI曲线。为更好地说明这一新方案的束匀滑效果,图中还给出了与传统SSD的比较。
从图6(a)中可以看出,互补旋转集束匀滑方案中焦斑的光通量对比度随着积分时间的增长迅速下降,而后达到稳定。这一快速匀滑方案达到稳定所需的时间仅为2 ps,远远小于SSD所需的数十ps。然而,焦斑的最终均匀性比SSD方案差,这是因为在旋转匀滑方案中焦斑的中心区域几乎不动而导致光通量对比度上升。图6(b)中的FOPAI曲线同样表明,在积分时间为20 ps(稳定匀滑)时,SSD的匀滑效果更好。值得指出的是,互补旋转集束匀滑方案的优势在于实现超快速匀滑,而并非均匀性的提高,且由于其致使散斑的快速重新分布,也对LPI有潜在的抑制作用。进一步分析图6可知,当集束中SPP拓扑荷数相同时,拓扑荷数的增大对于均匀性的提高并无明显改善,而当拓扑荷数不同时,集束焦斑的均匀性反而会下降,因而这一方案可采用相对简单的SPP结构参数,易于加工实现。
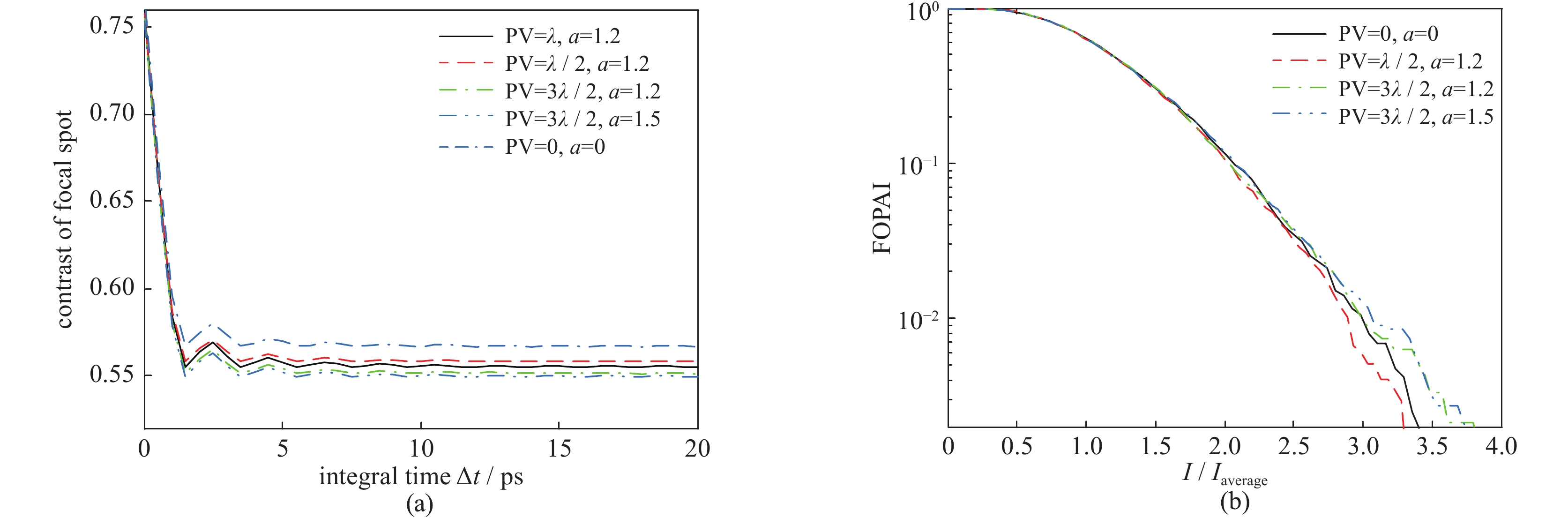
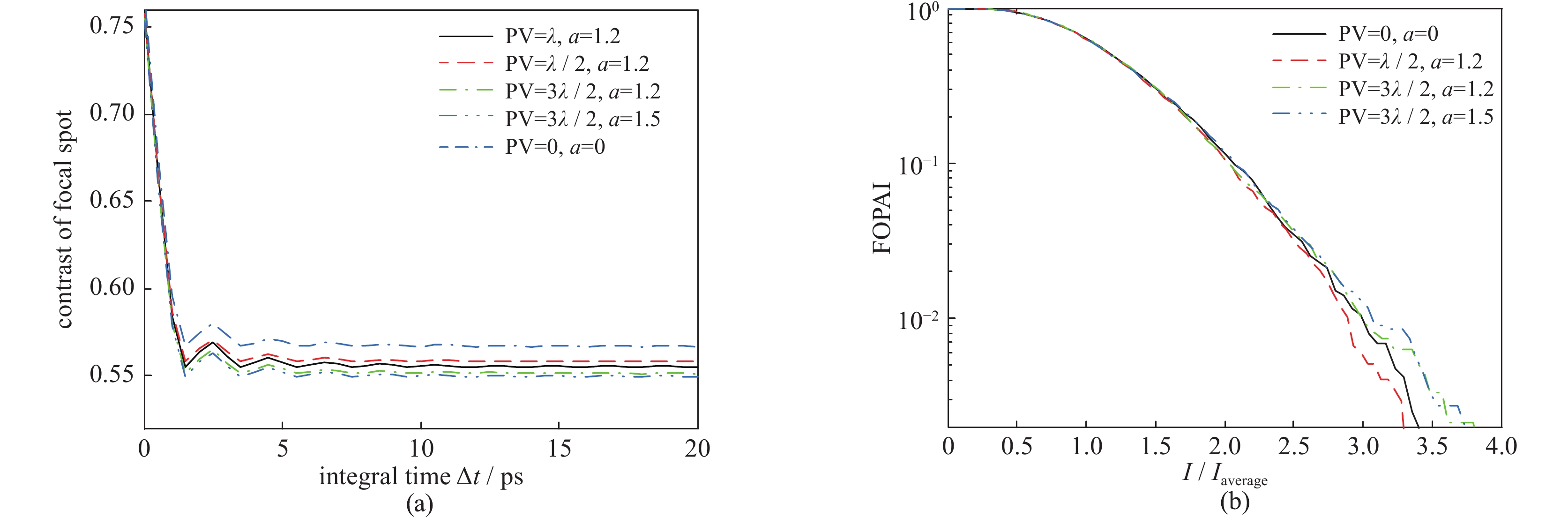
为了进一步考虑实际装置中激光束不可避免存在的振幅调制和位相畸变对该方案束匀滑性能的影响,图7给出了当不考虑CPP作用时,激光束的振幅调制度为1.2、位相畸变PV值为2π时,集束焦斑随时间的变化,图8则给出了不同振幅和位相畸变时,焦斑的光通量对比度和FOPAI曲线。
在图7中,集束焦斑的光强分布仍由多个“扇叶”组成,但由于振幅调制和位相畸变的存在,这些“扇叶”的形状和强度均产生一定程度的畸变,但其旋转周期却基本不随着振幅调制和位相畸变不同而改变。因此,可认为该方案在考虑光束振幅调制和位相畸变的情况下,仍可保持一定的束匀滑效果。图8(a)和(b)中给出在拓扑荷数和中心波长差不变的前提下,焦斑的光通量对比度和FOPAI曲线。可以看出,当考虑集束子光束的初始振幅调制和位相畸变时,焦斑的光通量对比度先随时间迅速减小而后达到稳定值。此外,当子光束的初始振幅调制和位相畸变控制在一定范围内时,焦斑的最佳光通量对比度在0.57附近振荡。
 图 8 不同振幅和位相畸变时,光通量对比度随积分时间的变化以及FOPAI曲线Figure 8. (a) Variation of the contrast of the focal spot with the integral time when the beamlets have different beam quality. PV denotes the peak-to-mean value of the wavefront distortion, and a denotes the max-to-mean value of the amplitude modulation. (b) FOPAI curves of the focal spot when the integral time is 5 ps
图 8 不同振幅和位相畸变时,光通量对比度随积分时间的变化以及FOPAI曲线Figure 8. (a) Variation of the contrast of the focal spot with the integral time when the beamlets have different beam quality. PV denotes the peak-to-mean value of the wavefront distortion, and a denotes the max-to-mean value of the amplitude modulation. (b) FOPAI curves of the focal spot when the integral time is 5 ps2.3 与径向匀滑方案的联用
尽管互补旋转集束匀滑方案在使散斑旋转方面具有极大优势,但其束匀滑性能仍是受限的,因而需要与其他束匀滑方案进行联用。
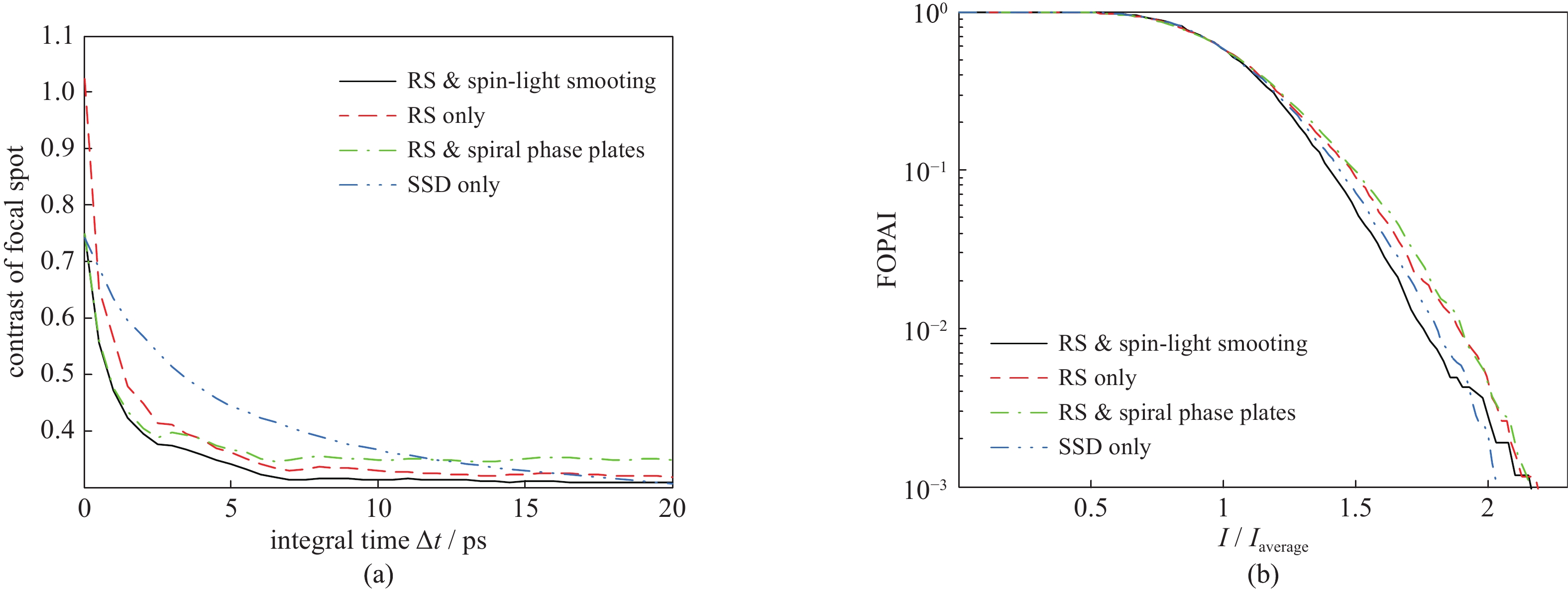
本文重点针对这一方案与我们曾提出的径向匀滑方案[15]的联用进行分析。在径向匀滑方案中,各子束经过ps量级周期性球面位相调制而产生快速变焦,从而使得焦斑内部散斑在径向上重新分布。因此,旋转集束匀滑与径向光束匀滑的联用将导致散斑同时在角向和径向得到匀滑。图9给出了当不考虑CPP作用时,两匀滑方案联用后的集束焦斑光强分布随时间的变化,图10(a)和(b)则分别给出了当考虑CPP作用时,两匀滑方案联用后的集束焦斑光通量对比度随时间的变化规律和FOPAI曲线。
图9表明,当旋转集束匀滑与径向光束匀滑方案联用时,不考虑CPP的集束焦斑光强分布仍然为数个大小和强度相同的“扇叶”,但它们会同时旋转和缩放。进一步考虑CPP对焦斑包络的控制作用,焦斑内部散斑会同时在角向和径向重新分布,则焦斑光强会同时在角向和径向得到匀滑,从而改善焦斑辐照均匀性,如图10(a)所示。图10(a)中,在两方案联用的情况下,焦斑光通量对比度随时间迅速下降而后达到一个稳定值,其束匀滑性能优于其他方案,而图10(b)给出的积分时间20 ps的FOPAI曲线也进一步说明了两方案联用的有效性。
由此可见,互补旋转集束匀滑方案的潜在应用方式之一是与径向匀滑方案联用。在这一新途径中,焦斑均匀性将从角向和径向两个方向得到快速改善,其束匀滑效果优于传统SSD技术。并且,焦斑内部小尺度散斑的光强及波长均以ps量级周期快速变化,从而为LPI的抑制提供了一种可能的途径。值得指出的是,在实际激光系统中,由于光束质量、位相元件加工质量和装调等问题,图1中子束1,3和2,4的焦斑不可能完美地在靶面互补填充,但每一个散斑可呈现为不同波长和偏振态的光斑的非相干叠加,仍然能有效地抑制LPI增长。相比于传统SSD技术,互补旋转集束匀滑方案的主要改进措施为:注入光源改为双频光源,并在终端光学组件中插入共轭SPP和CPP。当考虑这一新方案与径向光束匀滑方案的联用时,通过在主激光束预放大端插入装有硝基苯的石英比色皿和引入泵浦光源,即可在互补旋转集束匀滑方案的基础上引入径向光束匀滑方案,从而获得更优的束匀滑效果。
3. 结 论
本文提出了一种基于双频光源和涡旋相位板的互补旋转集束匀滑新方案。在这一方案中,激光集束中各个子束从超高斯光束变换成LG光束,且相邻两子束的拓扑荷数反号。利用一组共轭连续相位板阵列对集束进行空间相位调制,而双频光源为各个子束提供频移,从而通过子束间的拍频效应和共轭连续位相板的整形作用使得子束间两两相干的焦斑在靶面快速旋转且保持互补,达到ps量级快速角向匀滑的目的,特别是进一步与径向匀滑方案联用,不仅可迅速提升靶面辐照均匀性,甚至为抑制LPI提供一种可能的途径。
-
图 4 (a)原CPP和(b)共轭CPP的面型分布,(c)两光束分别经共轭CPP的焦斑光强分布
Figure 4. Surface shape of an original CPP (a) and its conjugate CPP (b). (c) is the far-field intensity distributions of a same laser beam after propagating through these two CPPs. Red regions shows the speckles generated by the original CPP, and green regions within the focal spot show the speckles generated by the conjugate CPP
图 8 不同振幅和位相畸变时,光通量对比度随积分时间的变化以及FOPAI曲线
Figure 8. (a) Variation of the contrast of the focal spot with the integral time when the beamlets have different beam quality. PV denotes the peak-to-mean value of the wavefront distortion, and a denotes the max-to-mean value of the amplitude modulation. (b) FOPAI curves of the focal spot when the integral time is 5 ps
-
[1] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Phys Plasmas, 2004, 11(2): 339-491. doi: 10.1063/1.1578638 [2] Haynam C A, Sacks R A, Moses E I, et al. National Ignition Facility laser performance status[J]. Appl Opt, 2007, 46(16): 3276-3303. doi: 10.1364/AO.46.003276 [3] Néauport J, Ribeyre X, Daurios J, et al. Design and optical characterization of a large continuous phase plate for laser integration line and laser megajoule facilities[J]. Appl Opt, 2003, 42(13): 2377-2382. doi: 10.1364/AO.42.002377 [4] Miyaji G, Miyanaga N, Urushihara S, et al. Three-directional spectral dispersion for smoothing of a laser irradiance profile[J]. Opt Lett, 2002, 27(9): 725-727. doi: 10.1364/OL.27.000725 [5] Munro D H, Dixit S N, Langdon A B, et al. Polarization smoothing in a convergent beam[J]. Appl Opt, 2004, 43(36): 6639-6647. doi: 10.1364/AO.43.006639 [6] Skupsky S, Short R W, Kessler T, et al. Improved laser-beam uniformity using the angular dispersion of frequency-modulated light[J]. J. Appl Phys, 1989, 66(8): 3456-3462. doi: 10.1063/1.344101 [7] Strozzi D J, Sepke S M, Bailey D S, et al. Inline modeling of cross-beam energy transfer and Raman scattering in NIF hohlraums[R]. Lawrence Livermore National Laboratory (LLNL), 2016. [8] Masson-Laborde P E, Monteil M C, Tassin V, et al. Laser plasma interaction on rugby hohlraum on the Omega Laser Facility: Comparisons between cylinder, rugby, and elliptical hohlraums[J]. Phys Plasmas, 2016, 23: 022703. doi: 10.1063/1.4941706 [9] Montgomery D S. Two decades of progress in understanding and control of laser plasma instabilities in indirect drive inertial fusion[J]. Phys Plasmas, 2016, 23: 055601. doi: 10.1063/1.4946016 [10] Weng X, Zhong Z, Li J, et al. Filamentation of spatiotemporal smoothed focal spot in plasma by Beam Smoothing scheme[J]. Optics Commun, 2019, 436: 216-221. doi: 10.1016/j.optcom.2018.12.039 [11] Allen L, Beijersbergen M W, Spreeuw R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Phys Rev A, 1992, 45(11): 8185. doi: 10.1103/PhysRevA.45.8185 [12] Fürhapter S, Jesacher A, Bernet S, et al. Spiral interferometry[J]. Opt Lett, 2005, 30(15): 1953-1955. doi: 10.1364/OL.30.001953 [13] Grier D G. A revolution in optical manipulation[J]. Nature, 2003, 424(6950): 810. doi: 10.1038/nature01935 [14] Gibson G, Courtial J, Padgett M J, et al. Free-space information transfer using light beams carrying orbital angular momentum[J]. Opt Express, 2004, 12(22): 5448-5456. doi: 10.1364/OPEX.12.005448 [15] Zhong Z, Yi M, Sui Z, et al. Ultrafast smoothing scheme for improving illumination uniformities of laser quads[J]. Opt Lett, 2018, 43(14): 3285-3288. doi: 10.1364/OL.43.003285 [16] Zhong Z, Hou P, Zhang B. Radial smoothing for improving laser-beam irradiance uniformity[J]. Opt Lett, 2015, 40(24): 5850-5853. doi: 10.1364/OL.40.005850 期刊类型引用(2)
1. 邹冬岩,熊皓,钟哲强,张彬. 基于相位板旋转排布的超快束匀滑方案. 中国激光. 2022(04): 57-66 .  百度学术
百度学术2. 高妍琦,李福建,季来林,赵晓晖,夏兰,冯伟,刘栋,史海涛,刘佳妮,饶大幸,崔勇,马伟新,隋展. 高功率激光驱动器光束匀滑技术研究(特邀). 红外与激光工程. 2020(12): 82-95 .  百度学术
百度学术其他类型引用(1)
-






 下载:
下载:
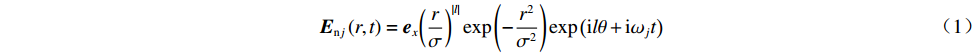
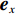
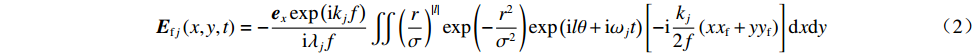
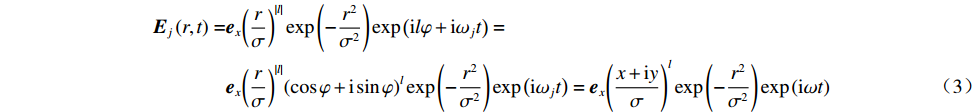
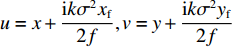
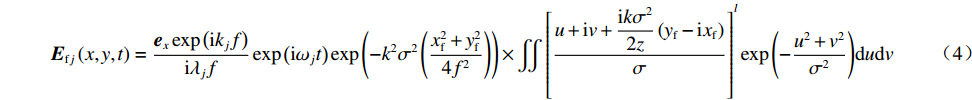
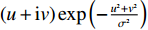
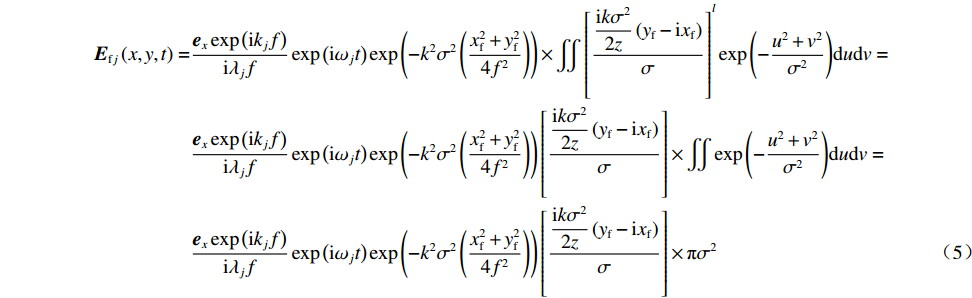
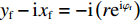
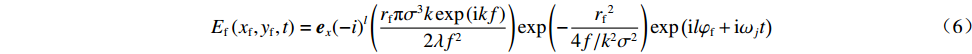
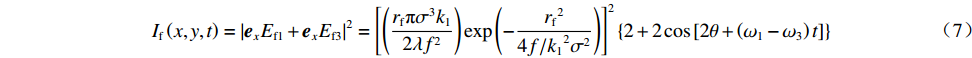
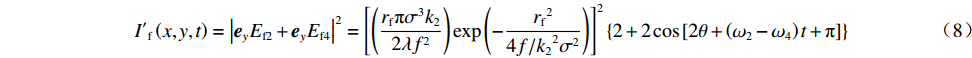
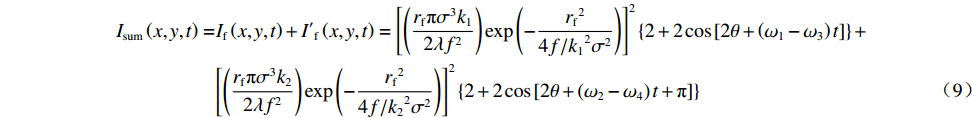
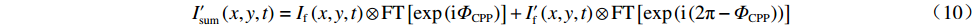








 下载:
下载: