A method for estimating coil resistance with pulsed strong electric current
-
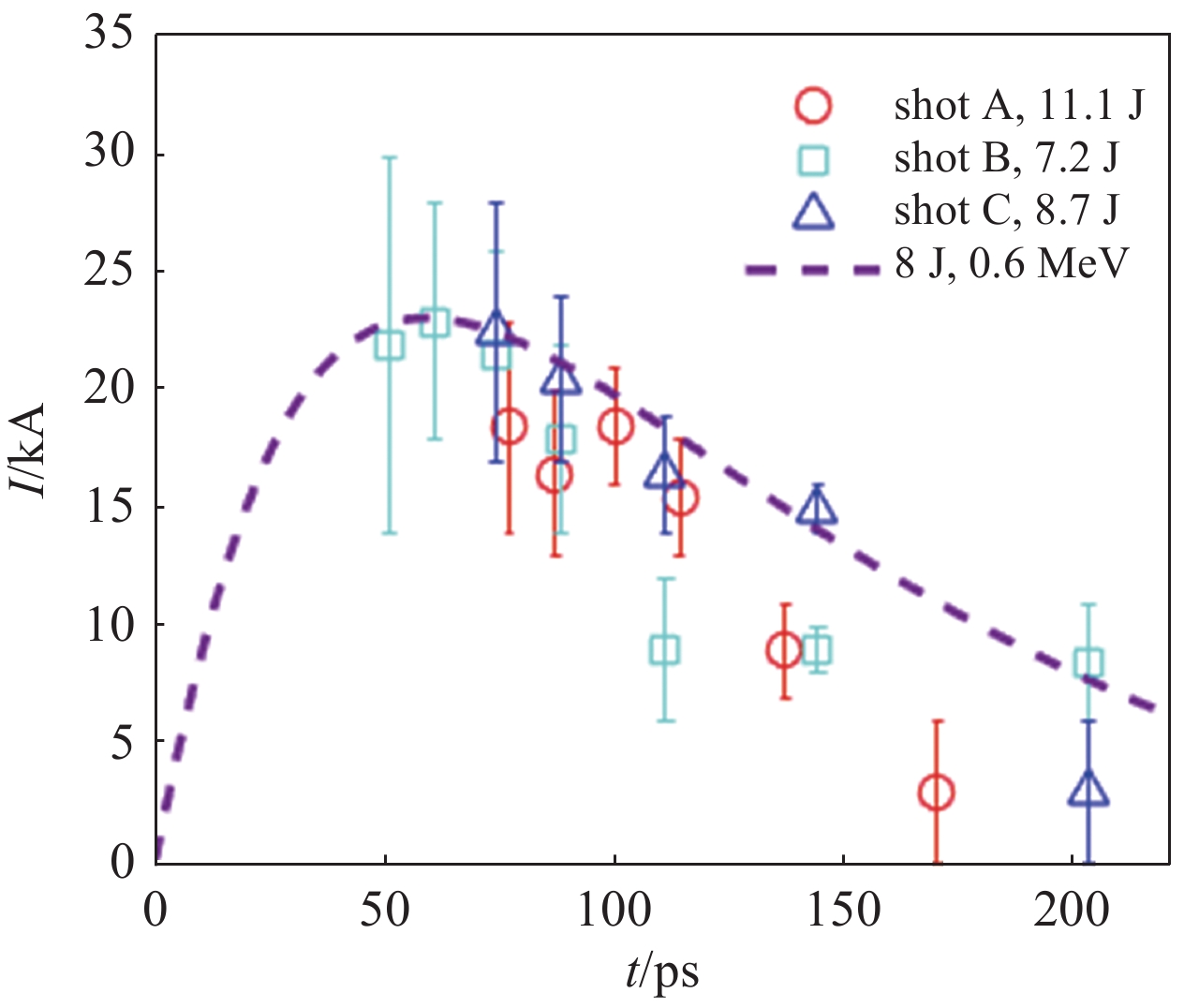
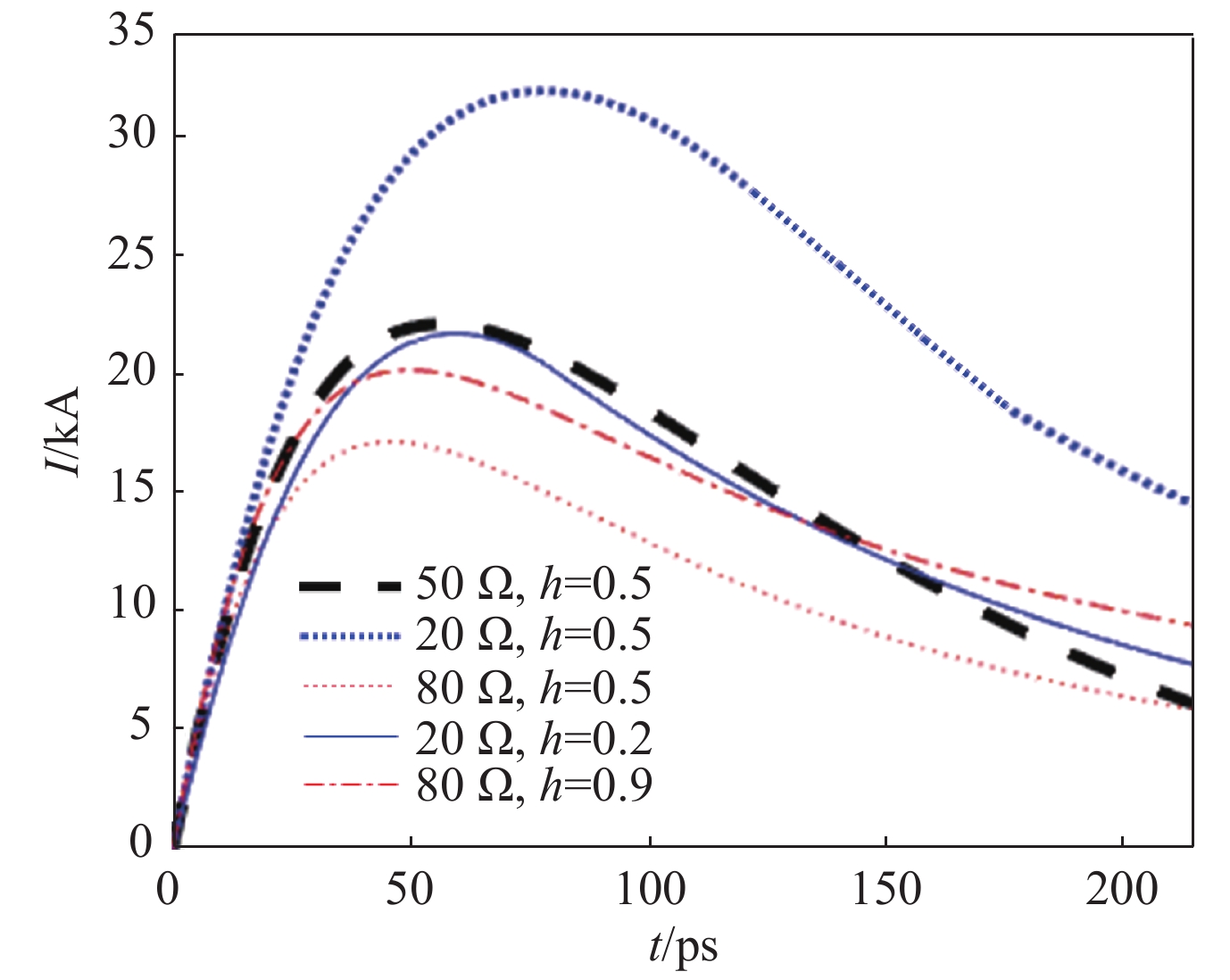
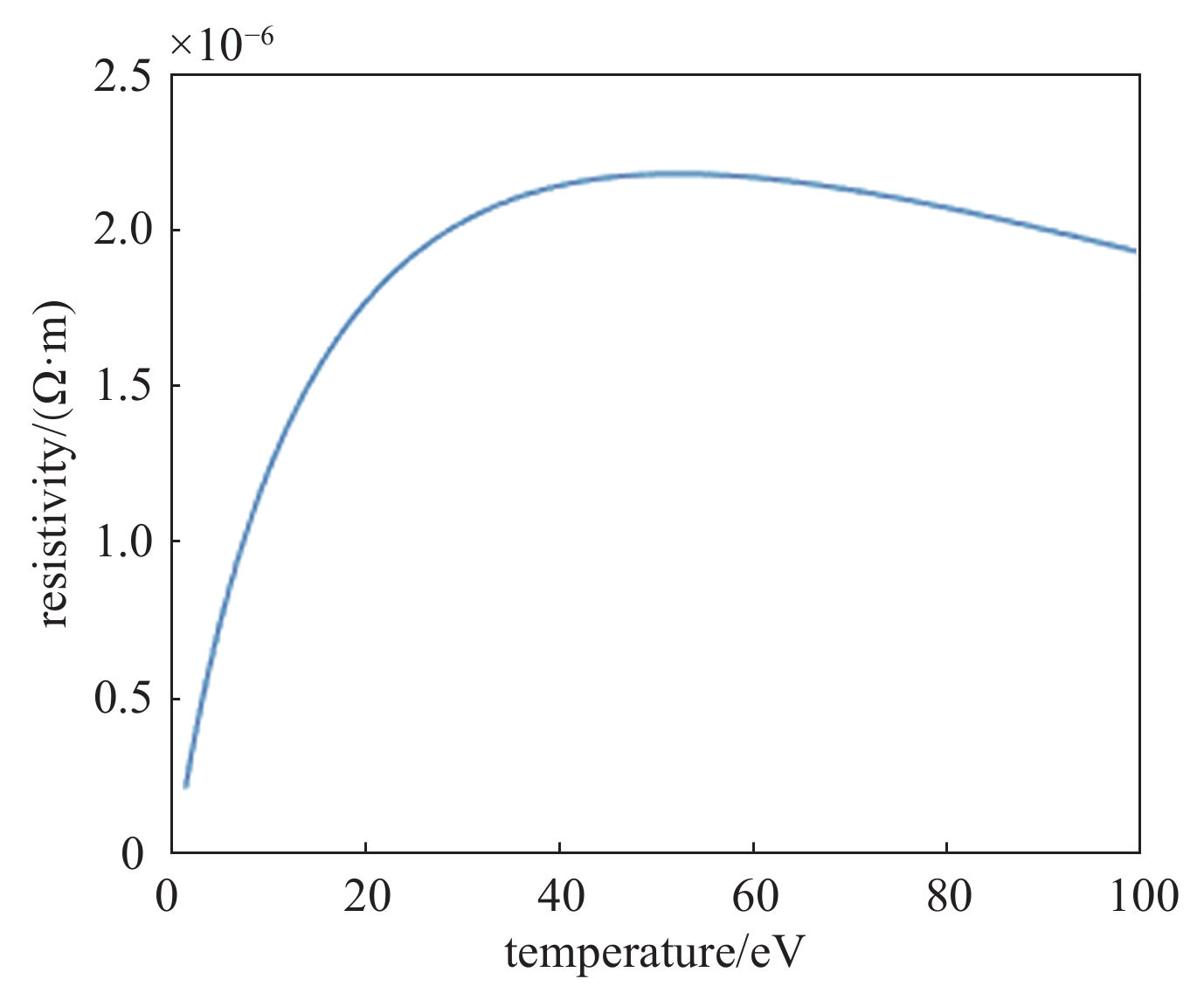
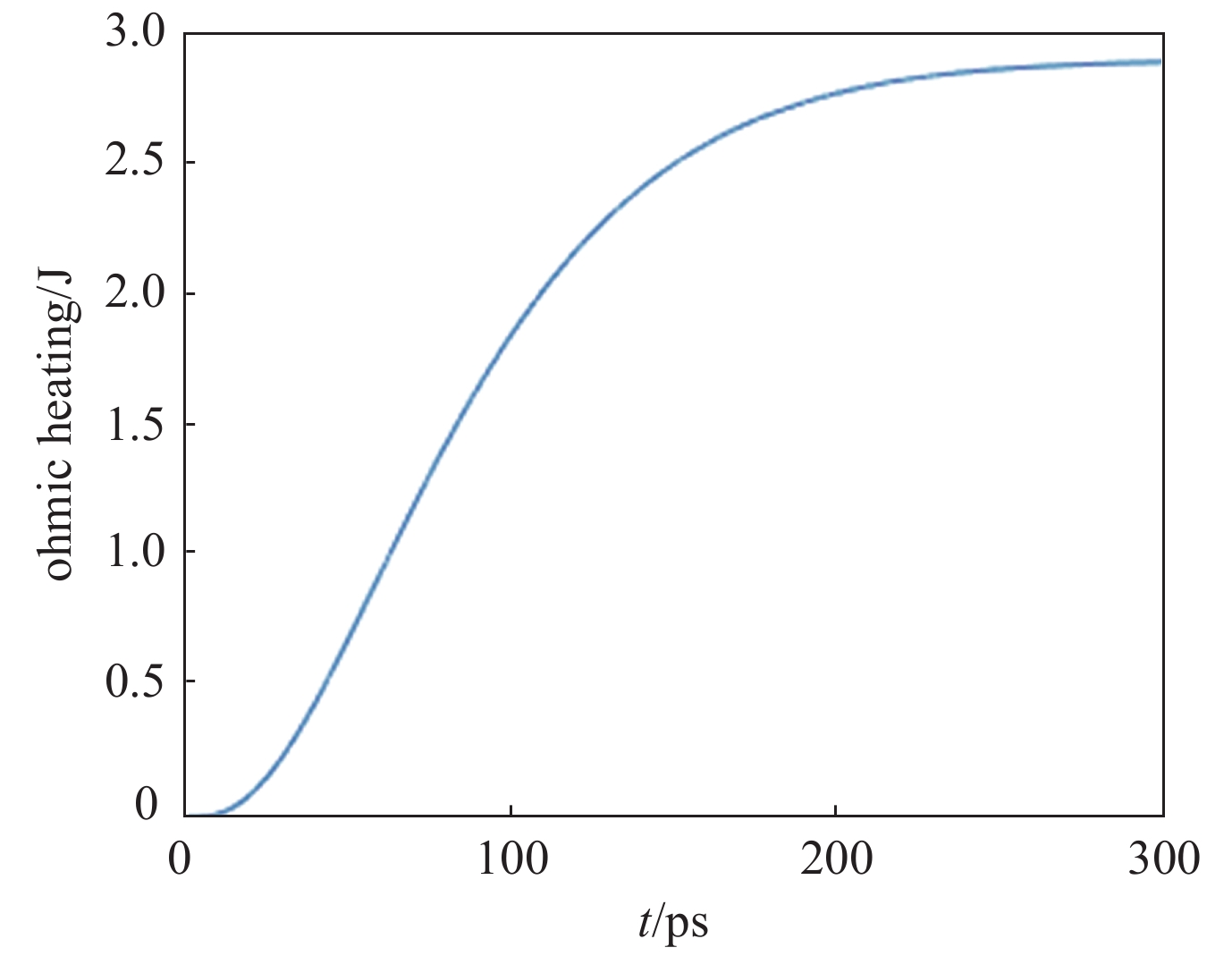
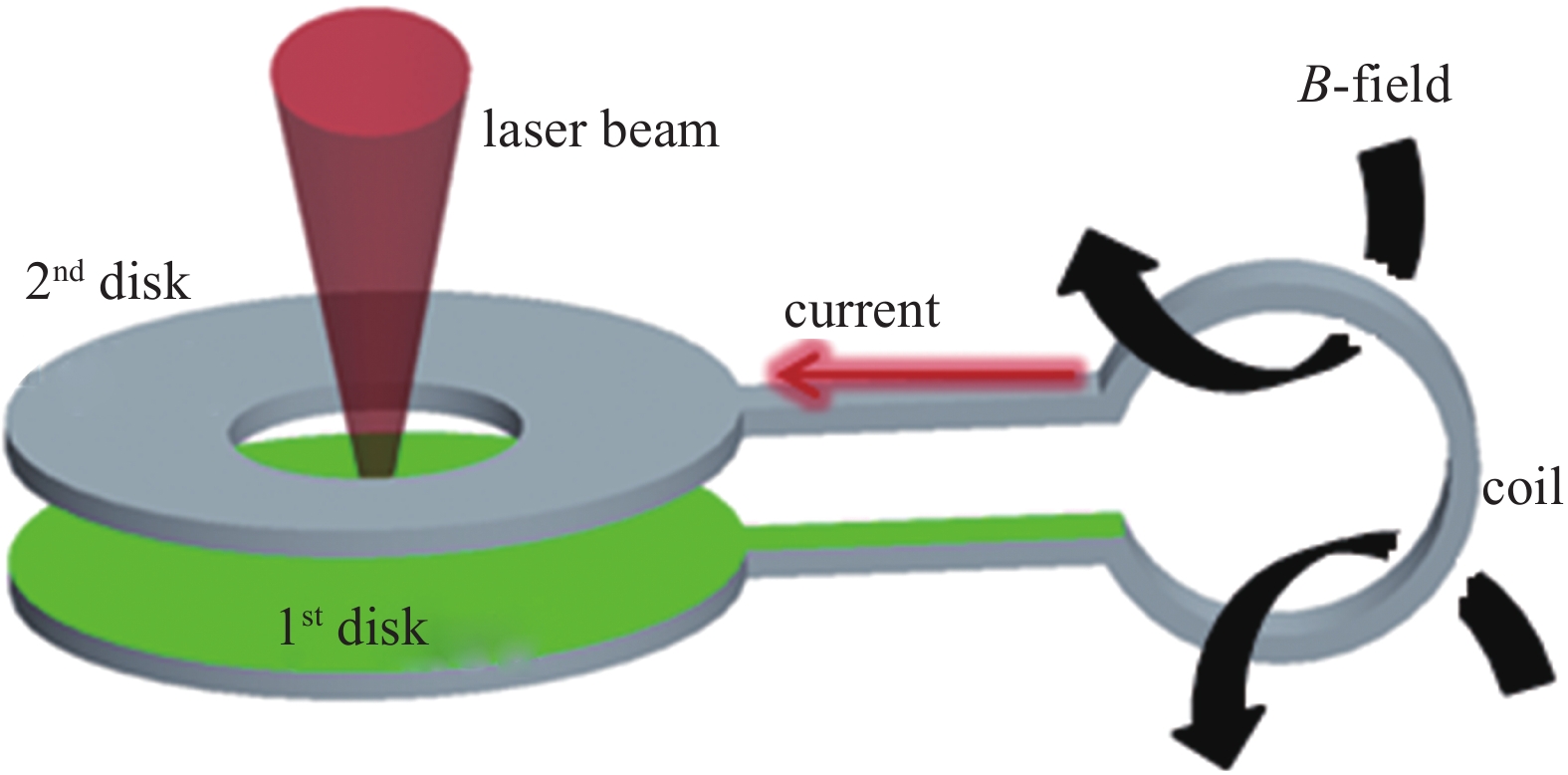
摘要: 在超强激光辐照电容线圈靶产生强磁场实验中，在约50 ps时，线圈电流达到20 kA以上。通过该实验结果与磁场产生理论模型对比，可得出该导线电阻值比常温直流电阻高出3个量级。对导线材料电阻率与趋肤效应的分析结果表明，该电阻值在量级上是合理的。获得超快脉冲强电流条件下的导线电阻值，有助于更深入理解线圈靶产生强磁场过程。Abstract: In experiments of strong magnetic field generation by laser irradiating capacitor-coil target, the coil current would be above 20 kA in ~50 ps. The coil resistance under this extreme condition can be obtained by comparing the current from experiments and the numerical model for magnetic field generation, which is three orders higher than that at room temperature. The result is reasonable when the coil resistivity and skin effect are considered. Coil resistance with pulsed strong electric current is important for investigating high magnetic field generation by using capacitor-coil target.
-
图 1 激光辐照电容线圈靶产生强磁场的原理示意图
Figure 1. Magnetic field generated by laser irradiating capacitor-coil target
图 2 三发次实验获得的电流随时间变化关系
Figure 2. Current in the coil inferred by proton radiography in three shots
图 3 通过磁场产生模型，得到不同导线电阻值和激光到电子能量转化率h条件下的电流随时间变化过程
Figure 3. Currents in the coil from the numerical model with different coil resistances and the fractions h of laser energy absorbed by the electrons
图 5 导线电阻为50 Ω时，导线通过电阻加热获得的总能量随时间变化曲线
Figure 5. Ohmic heating energy changes with time when coil resistance is 50 Ω
表 1 近几年实验激光条件及磁场结果
Table 1. Laser parameters and the corresponding magnetic field results in recent years
laser facility laser parameters magnetic field diagnostic method data origin energy/J wavelength intensity/（W/cm2） GEKKO-XII，Japan 1000 1ω 1×1015 1.5 kT@650 μm Faraday rotation Fujioka，2013[16] LULI pico 2000，France 500 1ω 1×1017 ～800 T B-dot probe Santos，2015[17] GEKKO-LFEX，Japan 880 1ω 3×1016 610 T proton radiography Law，2016[18] OMEGA，USA 2500 3ω 3×1016 50 T proton radiography Lan Gao，2016[19] OMEGA，USA 750 3ω 4.5×1015 210 T proton radiography Goyon，2017[20] 
下载: 导出CSV
-
[1] Mourou G A, Tajima T, Bulanov S V. Optics in the relativistic regime[J]. Rev Mod Phys, 2006, 78(2): 309-371. doi: 10.1103/RevModPhys.78.309 [2] Yu J Q, Lu H Y, Takahashi T, et al. Creation of electron-positron pairs in photon-photon collisions driven by 10-PW laser pulses[J]. Phys Rev Lett, 2019, 122: 014802. doi: 10.1103/PhysRevLett.122.014802 [3] Esarey E, Schroeder C B, Leemans W P. Physics of laser-driven plasma-based electron accelerators[J]. Rev Mod Phys, 2009, 81(3): 1229-1285. doi: 10.1103/RevModPhys.81.1229 [4] Lindl J D, Haan S W, Landen O L, et al. Progress toward a self-consistent set of 1D ignition capsule metrics in ICF[J]. Phys Plasmas, 2018, 25: 122704. doi: 10.1063/1.5049595 [5] Gilch P, Pollinger-Dammer F, Musewald C, et al. Magnetic field effect on picosecond electron transfer[J]. Science, 1998, 281: 982-984. doi: 10.1126/science.281.5379.982 [6] Huang Kai, Lu Quanming, Gan Lan, et al. Particle-in-cell simulations of magnetically driven reconnection using laser-powered capacitor coils[J]. Phys Plasmas, 2018, 25: 052104. doi: 10.1063/1.5021147 [7] Wang W M, Gibbon P, Shang Z M, et al. Magneticaly assisted fast ignition[J]. Phys Rev Lett, 2015, 114: 015001. doi: 10.1103/PhysRevLett.114.015001 [8] Daido H, Miki F, Mima K, et al. Generation of a strong magnetic field by an intense CO<sub>2</sub> laser pulse[J]. Phys Rev Lett, 1986, 56(8): 846-849. doi: 10.1103/PhysRevLett.56.846 [9] Zhang Zhe, Zhu Baojun, Li Yutong, et al. Generation of strong magnetic fields with a laser-driven coil[J]. High Power Laser Science and Engineering, 2018, 6: 38. doi: 10.1017/hpl.2018.33 [10] Bailly-Grandvaux M, Santos J J, Bellei C, et al. Guiding of relativistic electron beams in dense matter by laser-driven magnetostatic fields[J]. Nat Commun, 2018, 9: 102. doi: 10.1038/s41467-017-02641-7 [11] Shi Yuan, Qin Hong, Fisch N J. Laser-plasma interactions in magnetized environment[J]. Phys Plasmas, 2018, 25: 055706. doi: 10.1063/1.5017980 [12] Zhu B J, Li Y T, Yuan D W, et al. Strong magnetic fields generated with a simple open-ended coil irradiated by high power laser pulses[J]. Appl Phys Lett, 2015, 107: 261903. doi: 10.1063/1.4939119 [13] Zhu B J, Zhang Z, Jiang W M, et al. Ultrafast pulsed magnetic fields generated by a femtosecond laser[J]. Appl Phys Lett, 2018, 113: 072405. doi: 10.1063/1.5038047 [14] Yuan X X, Zhong J Y, Zhang Z, et al. Low-β magnetic reconnection driven by the intense lasers with a double-turn capacitor-coil[J]. Plasma Phys Control Fusion, 2018, 60: 065009. doi: 10.1088/1361-6587/aabaa9 [15] Wang W W, Cai H B, Teng J, et al. Efficient production of strong magnetic fields from ultraintense ultrashort laser pulse with capacitor-coil target[J]. Phys Plasmas, 2018, 25: 083111. doi: 10.1063/1.5000991 [16] Fujioka S, Zhang Z, Ishihara K, et al. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser[J]. Scientific Reports, 2013, 3: 1170. doi: 10.1038/srep01170 [17] Santos J J, Bailly-Grandvaux M, Giuffrida L, et al. Laser-driven platform for generation and characterization of strong quasi-static magnetic fields[J]. New J Phys, 2015, 17: 083051. doi: 10.1088/1367-2630/17/8/083051 [18] Law K F F, Bailly-Grandvaux M, Morace A, et al. Direct measurement of kilo-tesla level magnetic field generated with laser-driven capacitor-coil target by proton deflectometry[J]. Appl Phys Lett, 2016, 108: 091104. doi: 10.1063/1.4943078 [19] Gao Lan, Ji Hantao, Fiksel G, et al. Ultrafast proton radiography of the magnetic fields generated by a laser-driven coil current[J]. Phys Plasmas, 2016, 23: 043106. doi: 10.1063/1.4945643 [20] Goyon C, Pollock B B, Turnbull D P, et al. Ultrafast probing of magnetic field growth inside a laser-driven solenoid[J]. Phys Rev E, 2017, 95: 033208. doi: 10.1103/PhysRevE.95.033208 [21] Singh P K, Cui Y Q, Adak A, et al. Contrasting levels of absorption of intense femtosecond laser pulses by solids[J]. Scientific Reports, 2015, 5: 17870. [22] 张忠厚. 复杂电容器电容计算方法[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(4):701-704. (Zhang Zhonghou. Study on calculation method of complex capacitor[J]. Journal of Liaoning Technical University (Natural Science), 2010, 29(4): 701-704 doi: 10.3969/j.issn.1008-0562.2010.04.046 [23] Tichonchuk V T, Bailly-Grandvaux M, Santos J J, et al. Quasistationary magnetic field generation with a laser-driven capacitor-coil assembly[J]. Phys Rev E, 2017, 96: 023202. doi: 10.1103/PhysRevE.96.023202 [24] Amano Y, Miki Y, Takahashi T, et al. Isochoric heating of foamed metal using pulsed power discharge as a making technique of warm dense matter[J]. Rev Sci Instrum, 2012, 83: 085107. doi: 10.1063/1.4742986 [25] Davies J R, Bell A R, Haines M G. Short-pulse high-intensity laser-generated fast electron transport into thick solid targets[J]. Phys Rev E, 1997, 56(6): 7193-7203. doi: 10.1103/PhysRevE.56.7193 [26] Tuohy E J, Lee H T, Fullerton H P. Transient resistance of conductors[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(2): 455-462. [27] 赵凯华, 陈熙谋. 电磁学(下册)[M]. 第二版. 北京: 高等教育出版社, 1985: 587.Zhao Kaihua, Chen Ximou. Electricity and magnetism (Volume 2) [M]. 2nd ed. Beijing: Higher Education Press, 1985: 587 -
点击查看大图
图(5) / 表(1)
计量
- 文章访问数: 1649
- HTML全文浏览量: 363
- PDF下载量: 63
- 被引次数: 0
