高能电子照相（HEER）是利用GeV量级能量、皮秒脉宽的电子束透射成像，是高能质子照相外的另一种带电粒子无损检测及动态物理过程诊断技术^[1-2]，具有时间响应快、空间分辨率高等特点。相比高能质子照相^[3]，GeV放大型电子照相有可能实现更高的空间分辨率^[4]，有望进一步用于开展介观尺度的动态物理过程诊断，在极端条件下材料特性研究、惯性约束聚变、高能量密度物理诊断等领域有着广阔的应用前景^[5-13]。本研究采用Geant4模拟了电子与物质相互作用衰减等基本过程，设计了不同的含缺陷平板作为模拟客体，开展了放大型电子照相系统缺陷分辨能力研究，评估了电子照相对实心客体的探测分辨能力。

1.   基于开源蒙特卡罗Geant4电子照相模拟

1.1   电子照相关键物理过程

对于电子与物质相互作用主要考虑：轫致辐射、多次库伦散射、电离这3个过程^[14]，Geant4^[15] physics.cc 关键定义如下：

pmanager->AddProcess （new G4eMultipleScattering（），−1，1，1）；

pmanager->AddProcess （new G4eIonisation（），−1，2，2）；

pmanager->AddProcess （new G4eBremsstrahlung（），−1，3，3）。

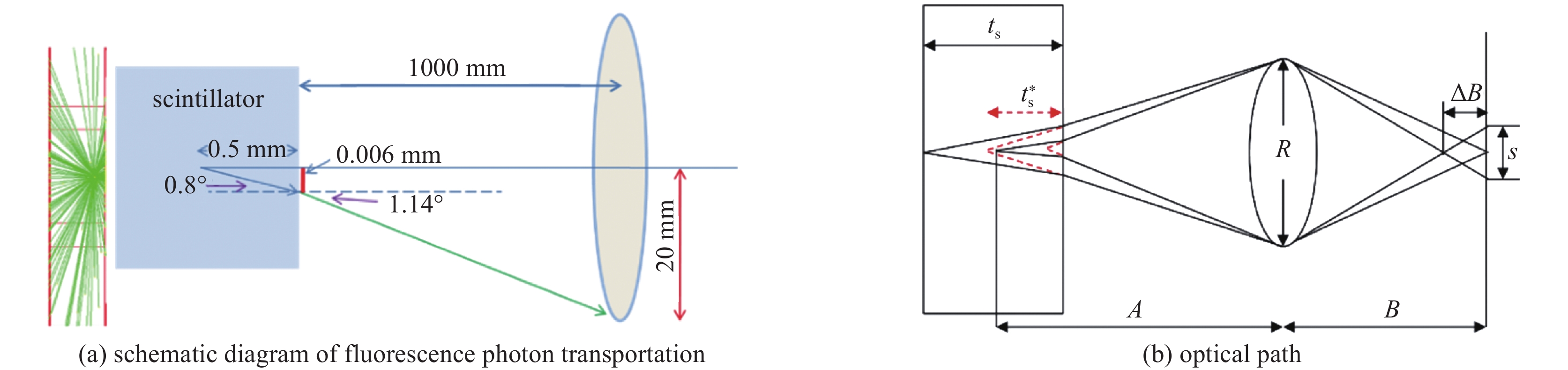
由于电子能量较高，考虑到模拟效率并未采用Livermore标准电磁模型。此外，次级轫致辐射X射线产生的二次电子不计入内。穿透客体的电子最终到达探测器，一般探测器均采用平板闪烁体记录电子二维空间分布，将电子通量信号转化为荧光分布最终由CCD采集。考虑到对荧光模拟将占用大量计算资源，提前计算不同能量电子入射闪烁屏时的能量沉积分布，模拟成像时仅模拟电子穿过客体后的二维空间通量分布，再卷积闪烁屏响应获得照相结果。电子在荧光平板闪烁体内呈各向同性分布，如图1所示（左侧）。

图  1  电子在闪烁板内激发荧光后，光输运所致景深模糊示意图

Figure  1.  Schematic diagram of blurring caused by light transport after electrons excited fluorescence in scintillator

下载: 全尺寸图片 幻灯片

如图1所示，由于闪烁板存在一定厚度，最终光信息传输过程中将存在一定景深模糊，模糊量为

式中：R为后端接收透镜的半径；t_s为闪烁板半厚度；${t_{\rm{s}}}^*$（$\Delta A = {t_{\rm{s}}}^*/2$）为不考虑折射率时的替代厚度；N为折射率（$N = {t_{\rm{s}}}/{t_{\rm{s}}}^* = 1.58$）；A为闪烁板后断面至透镜距离；M（B/A）为透镜光路放大倍数。假设典型的参数如图1（a）所示，对于图1所示景深模糊大致为0.003M mm。取3倍放大倍数即M＝3，综合考虑CCD最小成像单元及景深模糊所致量化误差，综合取虚拟电子探测器最小可分辨尺寸为0.01 mm。

1.2   电子照相结构与束流参数

将四极透镜简化为圆柱结构，不考虑四极透镜磁场边缘效应。电子在一段四极透镜内的运动径迹如图2所示。在虚拟探测平面上，采用Geant4灵敏探测器（SD-detector）模块，构建总尺寸为40 mm×40 mm，像素尺寸为0.01 mm，总像素单元4000×4000的灵敏阵列式探测器。

图  2  电子穿过四极透镜组的可视化轨迹（Geant4_openGl显示）

Figure  2.  Visualization of electron trajectories through quadrupole lenses （Geant4_openGl）

下载: 全尺寸图片 幻灯片

1.5 mm半径均匀场，1 mrad弥散角，能量2.5 GeV±2.5 MeV高斯分布，到达探测器时通量为10000/可分辨像素（0.01 mm×0.01 mm）。

2.   成像模拟客体设置

2.1   缺陷样品及其基本参数

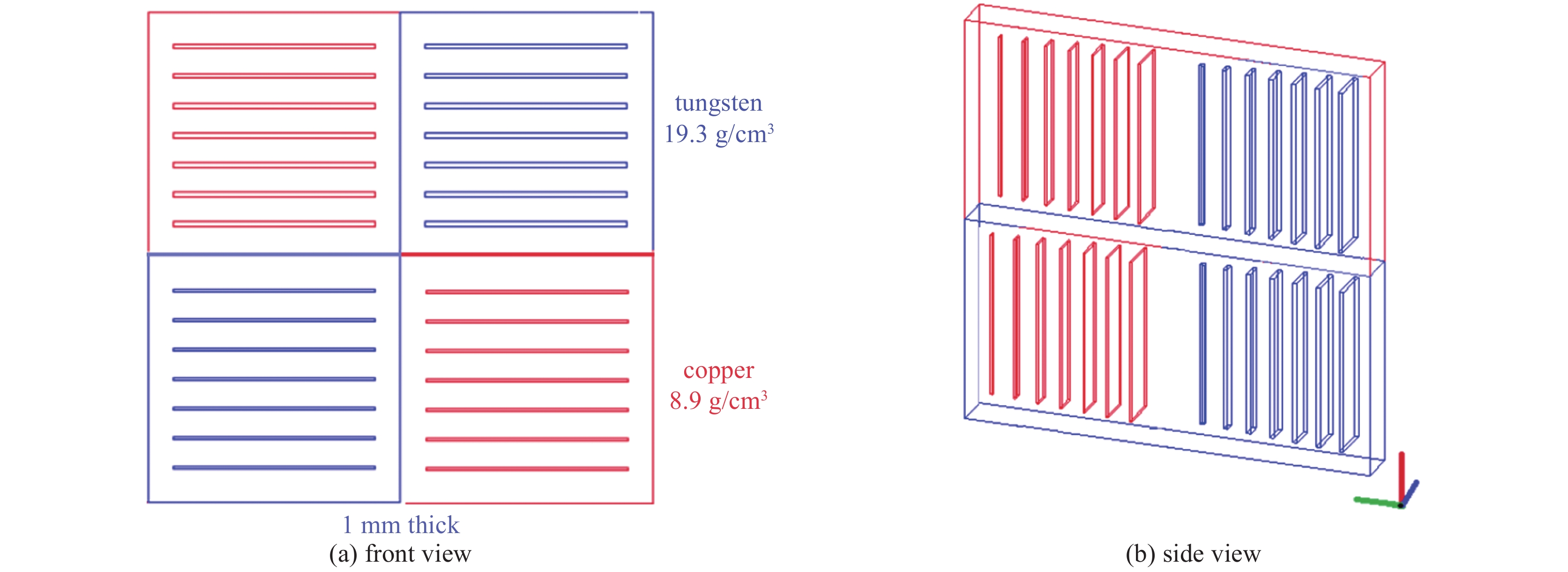
设置一定厚度平板，内含不同厚度空隙样品共4块，横向尺寸均为1 mm×1 mm，其中2块厚度为1 mm 纯钨，对应面密度为1.935 g/cm²，2块1 mm厚纯铜，面密度为0.89 g/cm²纯铜。相同材料钨板其含空隙宽度不同，分别为0.005 mm与0.001 mm，7条空隙厚度分别为0.1，0.25，0.4，0.55，0.7，0.85，1 mm。两铜板内空隙设置与钨板一致，4块样品Geant4_openGL可视化如图3所示。入射电子束均匀覆盖整个样品。

图  3  4块含不同空隙样品（Geant4_openGl显示）

Figure  3.  Four samples with different voids （Geant4_openGl）

下载: 全尺寸图片 幻灯片

2.2   台阶样品及其基本参数

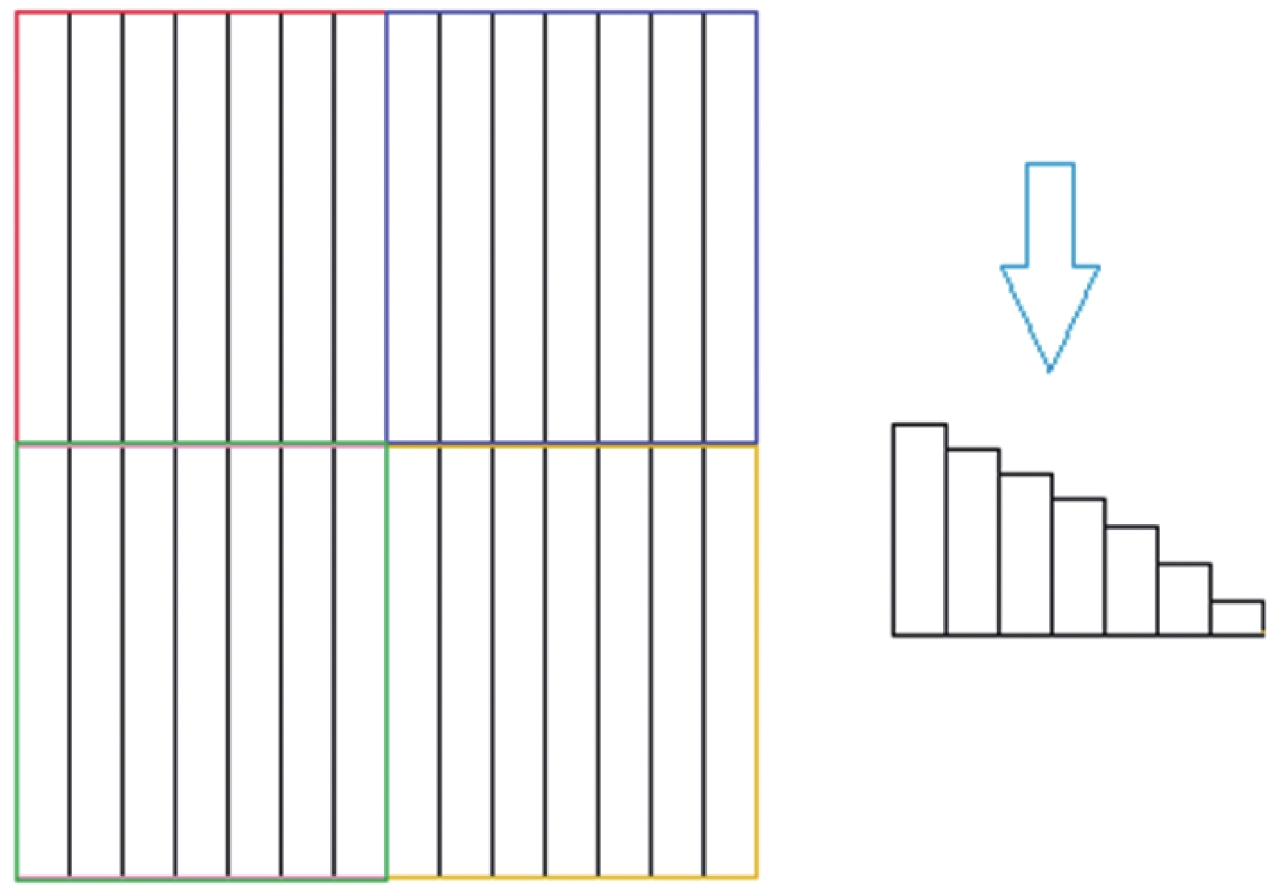
设置4块台阶样品，材料分别为纯钨与纯铜各2块，相同材料的2块台阶样品台阶厚度分别为0.10，0.25，0.40，0.55，0.70，0.85，1.00 mm；1.10，1.25，1.40，1.55，1.70，1.85，2.00 mm，模拟时相同材料台阶样品置于右上-左下（图4绿色与蓝色区域）或者左上右下（图4红色与黄色区域）。入射电子束为线源，水平投射至上下部台阶样品中心位置，以获得该成像条件下的线扩散函数。

图  4  钨与铜台阶样品示意图

Figure  4.  Schematic diagram of tungsten and copper step samples

下载: 全尺寸图片 幻灯片

3.   Geant4模拟电子照相结果

3.1   纯钨与纯铜板最小可分辨缺陷与面密度

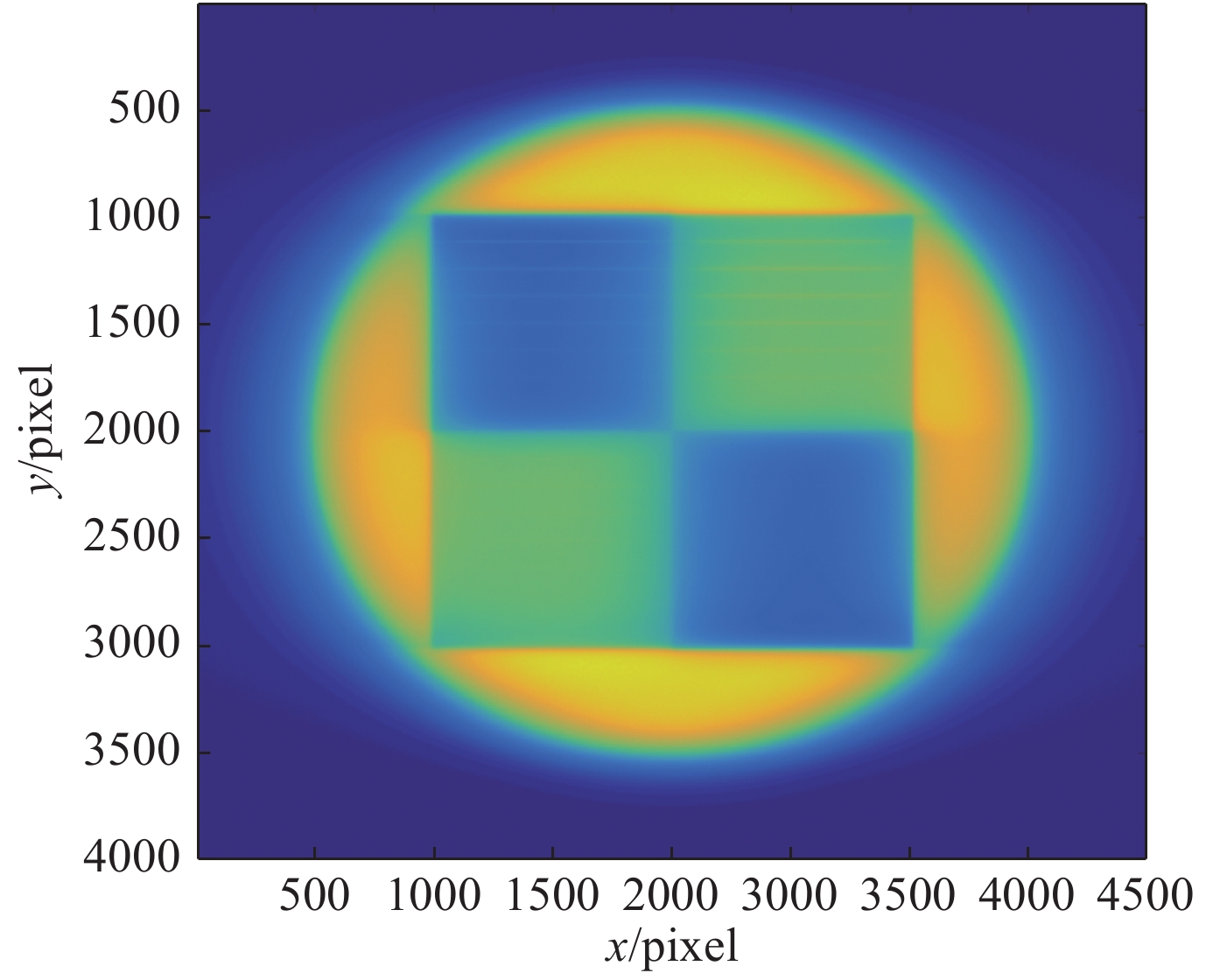
使用Geant4，openmpi，32线程2680X2计算约80 h得到，其中电子通量为10000/可分辨像素（0.01 mm×0.01 mm），像素统计方差＜3%，模拟得到投射图像如图5所示。

图  5  钨与铜缺陷板投射图像

Figure  5.  Projection image of tungsten and copper defect plate

下载: 全尺寸图片 幻灯片

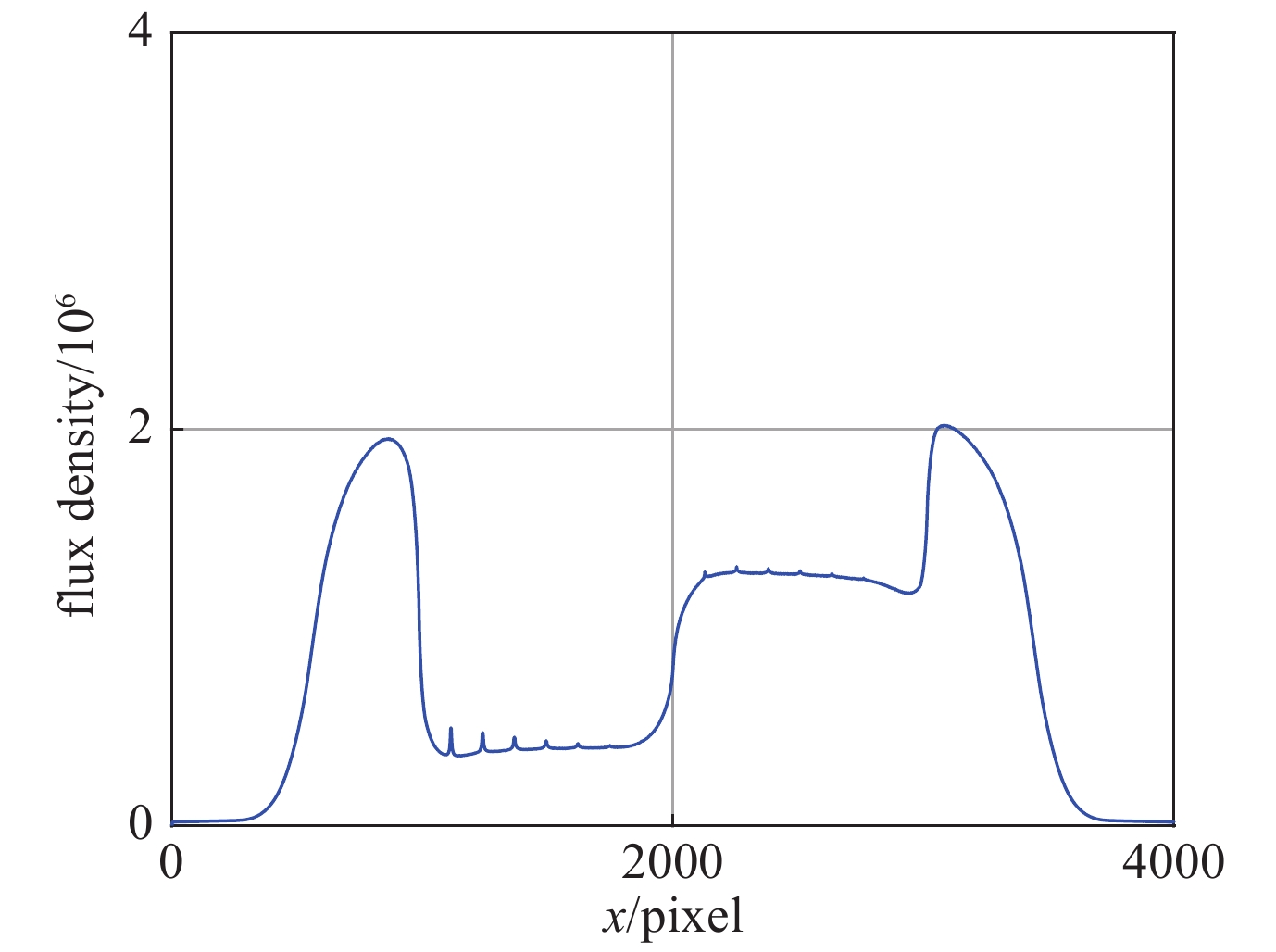
由于电子能量及出射角度均存在一定分布，假设电子束流为圆形均匀分布，实际到达探测面时成部分椭圆状并存在一定模糊，束流覆盖区域外仍有粒子分布。从对缺陷的诊断上讲，宽度为0.01 mm，厚度在0.4 mm以上的空隙，在面密度为1.935 g/cm²的纯钨与0.89 g/cm²纯铜板投射图像上均有体现，而宽度为0.005 mm空隙，均难以直接用肉眼甄别。取左半侧（上半部分为狭缝宽0.01 mm的钨板，下半部分为狭缝宽度为0.005 mm铜板）中心处电子通量密度如图6所示。

图  6  电子通量密度

Figure  6.  Electron flux density

下载: 全尺寸图片 幻灯片

由图6可知，若不存在客体，则电子通量分布应近似为矩形，由于分别阻挡了钨板与铜板（左与右），电子通量分别下降约75%与40%。狭缝中最厚的为1 mm，相当于对射线没有阻挡，理想情况下电子强度应没有下降。然而钨板最左侧狭缝（坐标1180）对应电子强度峰值仅较附近钨阻挡区域电子通量高不足20%，远小于400%这一理想值（达到2×10⁶）。由于狭缝为0.01 mm，厚度为1 mm，长径比为100，有部分电子可能穿过狭缝壁能量有所丢失，故峰值强度比理想值小。另一方面，若电子能够通过磁场精确聚焦，所获得图像中对应狭缝处的峰值应与原电子束强度一致，其他区域模糊影响只会与该峰叠加，增加其半高宽而并不会明显影响峰强度。随着狭缝空隙厚度减小至0.4 mm以下，图像上就无法识别狭缝。此外，若狭缝宽度进一步缩至0.005 mm，即使面密度较低的铜板，电子穿过后造成的模糊已将微弱的投射信号湮灭，相对应狭缝显示毛刺状分布。

3.2   纯钨与纯铜台阶样品及束流线扩展函数

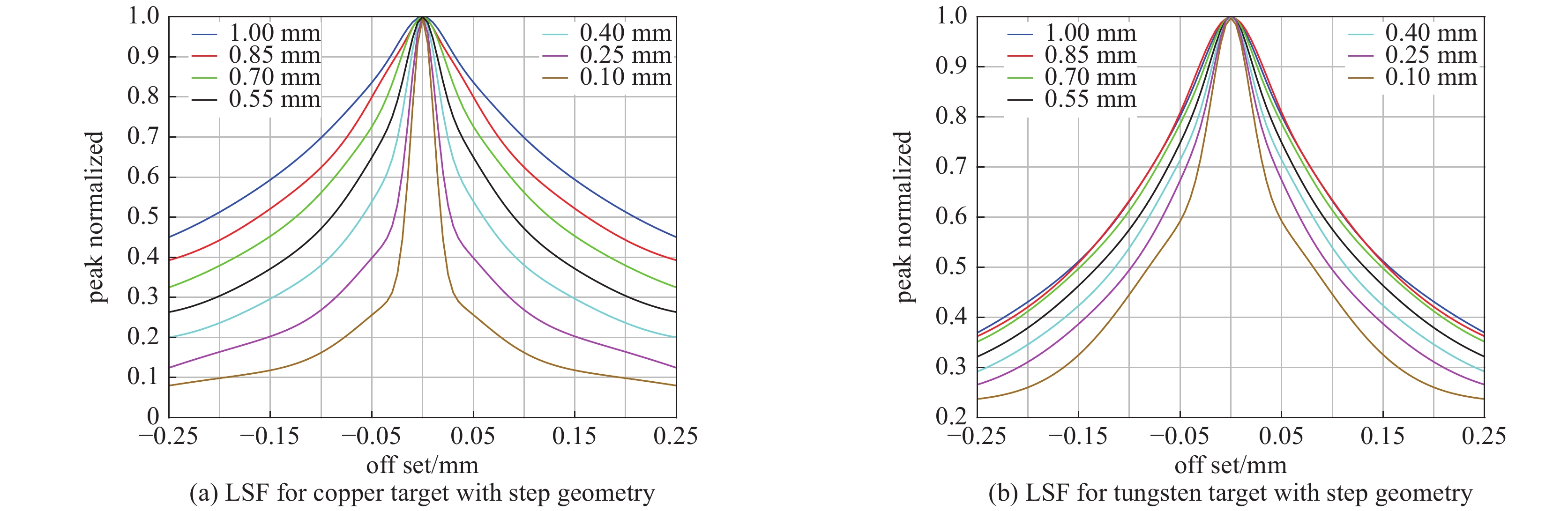
图7为台阶样品线源照相图，其中光色方框（0.7 mm×0.7 mm）对应铜台阶样品，右上为0.1～1.0 mm，左下为1.1～2.0 mm；白色方框对应钨台阶样品，左上为0.1～1.0 mm，右下为1.1～2.0 mm。由模拟结果可知，当台阶样品为钨且大于1 mm时，线扩散函数基本为分布展宽较大。而铜台阶样厚度大于1 mm时，线扩散函数也有较明显展宽，这里只给出0.1～1.0 mm的钨与铜台阶样品的线扩散函数，如图8所示。

图  7  钨与铜台阶样品线源透射图像

Figure  7.  Line source transmission image of tungsten and copper stepped samples

下载: 全尺寸图片 幻灯片

图  8  抛光前后光束取样光栅衍射效率分布图

Figure  8.  Diffraction efficiency map of a BSG pre-polishing and post-polishing at 532 nm

下载: 全尺寸图片 幻灯片

对比图8（a）与图8（b）可知，随着台阶样品厚度增加，线扩展函数半高宽增大（图8（b）中0.85 mm与1.00 mm扩展函数的特例是由于峰值归一化时噪声过大所致）。相同厚度台阶样品，密度越高其线扩散函数展宽/模糊越大。

图8（a）中厚度为0.1 mm铜台阶线扩散函数半高宽约为0.015 mm，即模糊宽度为0.015 mm，而图5中对应缺陷宽度0.01 mm可以用肉眼识别，二者并不矛盾。首先，除半高宽外定义图像空间分辨率还有其他方法，如10%对比可见的瑞利判据，半高宽与分辨单元的关系对于严格三角形展宽分布是可以严格证明的，然而，实际线扩散函数均存在拖尾现象，半高宽只是对最小可分辨单元的估计。其次，直接线扩散函数针对电子束穿过实体样品后的弥散，而可分辨最小空隙受非空隙区域影响很大，且还与空隙长径比、磁场色散系数等相关（可能会出现边界锐化增强等现象）。因此，对于不同待测样品，应根据具体分辨需求模拟评估系统相应空间分辨能力。

4.   结　论

模拟研究了2.5 GeV电子照相的关键物理过程，采用Geant4构建了输运、电子与物质相互作用衰减等基本过程，设计了不同材料、不同厚度的含缺陷平板作为模拟客体，开展了放大型电子照相系统缺陷分辨能力模拟研究。此外模拟获得了电子束流穿过相应面密度材料后的线扩展函数，进一步评估了电子照相对实心客体的探测分辨能力。

由于电子照相空间分辨率除电子在物体中的多次库伦散射外，能量弥散所致色差也会影响实际分辨效果，采用线扩散函数仅能大致估计其空间分辨率，涉及复杂样品空隙分辨时还需对样品进行实际全物理过程照相模拟予以评估。