Orbit correction based on machine learning
-
摘要: 轨道校正是加速器束流调节最基本的步骤之一,也是目前各加速器实验室共同面对的问题之一。在传统方法中,线性代数工具被应用于各种类型的响应矩阵,以解决响应矩阵的奇异性等问题。提出一种基于机器学习的加速器轨道校正方法,可以避免处理响应矩阵的问题通过直接读取BPM数据和校正磁铁强度值实时构建机器学习模型快速地对轨道进行修正。对机器学习的轨道校正方法进行了介绍,并从数学公式、算法模型、在模拟和真实数据上的测试等方面对该方法进行了讨论。结果表明,在误差范围内该方法能有效的对加速器束流轨道进行校正。Abstract: Orbit correction is one of the most fundamental processes used for beam control in accelerators. Algorithms have been developed at various laboratories to meet specific demands. Typically, linear algebraic tools are applied to various response matrices to solve related problems. However, there are still many problems faced by orbit correction algorithms such as lengthy measurement and computation time. A new approach based on machine learning to develop an orbit correction program is introduced. In this method a machine learning program is trained with correctors data and BPMs data for applying to orbit correction. Mathematical formulation, algorithms prototyped and tested on simulated and real data, and future possibilities are discussed.
-
Key words:
- orbit correction /
- machine learning /
- operation data /
- magnet error /
- data cleaning
-
在粒子同步加速器中,由于磁铁的二极场误差和各磁铁的准直误差等,粒子通常偏移理想轨道运转形成轨道畸变,导致机器性能降低甚至出现故障。好的轨道是加速器运行的基础,轨道校正是当前加速器束流调节最基本的步骤,也是目前研究最广泛的领域之一[1]。国际上各个实验室已经开发了各种算法来满足特定的需求。一些算法比如SVD,MICADO等已经比最初的需求有了更广泛的适用性,并且在经过发展后在各个加速器实验室中被使用起来[2-3]。
随着近年来的发展,加速器逐步朝着能量越来越高、周长越来越大、亮度越来越高等方向发展,机器的运行成本也越来越高,一些传统的技术和方法也逐渐面临一些局限,比如不能够足够快地响应加速器状态的变化,或所耗机时等成本高等。近年来计算机软硬件技术的迅猛发展,计算机计算和存储技术有了很大提升,加速器历史数据的数据量和数据质量都有了很大的改善,使一些基于机器学习的新的方法应用到加速器中以提高加速器性能和自动化程度成为可能[4]。因此,本文提出了一种使用机器学习的轨道校正方法。该方法直接读取运行数据中的校正磁铁强度数值和对应的束流位置探测器(BPM)数值构建机器学习模型,将BPM数值作为模型的输入,校正磁铁强度作为模型的输出,用模型的输出对轨道校正所需的校正磁铁强度进行预测,能够实时地读取BPM和校正磁铁的数据直接对轨道进行校正,并能实时读取BPM和校正磁铁数据对模型进行更新以响应加速器各系统状态的变化,通过引入L2范数正则化的方法解决BPM之间存在多重共线性的问题。模拟仿真实验和真实数据的检验结果表明,该方法可行,且模型预测精度高,计算速度快,计算速度较传统算法SVD有很大提升,将可能是一个有潜力的研究方向。进行多次试验得到了一致的结果,模型有很好的鲁棒性。
1. 传统方法
传统方法通常包含以下几个步骤:(1)选择需要使用的BPM和校正磁铁;(2)测量响应矩阵;(3)测量实际轨道;(4)确立目标轨道;(5)计算期望闭轨校正量;(6)利用响应矩阵计算校正磁铁强度;(7)检查校正磁铁强度是否超限;(8)施加校正磁铁电流。
轨道校正通常需要满足以下方程
‖r‖2=‖z−Rθ‖22 (1) 式中:r为轨道校正残余误差;z为期望轨道校正量;R为BPM处轨道对校正磁铁强度变化的响应矩阵;θ为校正磁铁变化强度。
若响应矩阵R不满秩,则RTR为奇异矩阵,不可直接求其逆矩阵。通过奇异值分解
R=USVT=∑iλiuivTi (2) 式中:U=[u1,…,um]为m阶正交矩阵;V=[v1,…,vn]为n阶正交矩阵;S为m×n的对角矩阵。易得广义矩阵R+为
R+=∑i1λiviuri=Vdiag(1λi,⋯,1λr,0,⋯,0)Ur (3) 去除接近零的奇异值可以得到性能较好的广义矩阵,从而得到稳定的最小二乘解
θ=R+z ,该方法即为传统的SVD方法[5-6]。该过程即为响应矩阵的病态问题及基于奇异值分解的解决方法。这类方法通常以测得的响应矩阵为基础,对响应矩阵进行变换以得到广义矩阵R+来对轨道进行直接的控制。因此,响应矩阵失效或出现变化时,广义矩阵R+则不能继续对轨道进行有效的校正。另一方面,相较于直接对BPM数据和校正磁铁强度值构建机器学习模型并采用L2范数惩罚项以避免矩阵奇异性的方法,通过测量响应矩阵再进行奇异值分解的方法其算法的复杂度明显较高,奇异值分解的过程将带来更多的时间消耗。同时,奇异值分解的过程中,奇异值数量的选取也会给结果带来影响:若奇异值选取过少,则可能带来广义矩阵的偏差;若奇异值选取过多,则可能使得很小的BPM测量误差就带来很大的影响。因此,本文提出了一种更灵活的基于机器学习的轨道校正方法。
2. 基于机器学习的轨道校正流程
通过机器学习对加速器运行数据进行挖掘,使用运行数据中的信息通常是一个有效的办法。基于机器学习的加速器调节方法主要包含以下几个步骤:数据集的收集、数据的清洗、构建机器学习模型及训练、模型交叉验证、将预测设置值输入到虚拟或真实机器中[7]。本文用模拟数据对模型进行训练,用MADX模拟仿真进行原理验证;用BEPCⅡ (北京正负电子对撞机重大改造工程)历史数据进行模型训练,用真实值进行检验。
模拟验证包含以下过程:用BEPCⅡ储存环Lattice导入随机的磁铁误差以模拟加速器不同状态下的运行环境,输入不同的校正磁铁强度组合模拟运行过程,记录好对应的BPM和校正磁铁数据完成数据收集;利用已开发的Python环境下的机器学习平台工具对数据进行清洗合并;选择并构建合适的机器学习模型将BPM和校正磁铁数据输入训练、构建模型;对模型进行交叉检验;向模型输入一组期望的轨道数据,模型预测出一组对应的校正磁铁设置值;将预测的结果输入到Lattice中进行动力学的模拟计算检验;保存模型。
真实机器检验的过程:从运行数据调取对应的校正磁铁设置值和BPM数据;对数据进行清洗和合并;调用对应的模型进行训练;输入一组预期的轨道,模型预测出需要的校正磁铁设置值;用模型预测的校正磁铁设置值和真实的设置值对比,分析其误差。
3. 数据收集与清洗
储存环的闭轨畸变来源于各类磁铁的二极场误差和各类磁铁的准直误差,其中最主要的来源为四极铁的准直误差[8]。本文参考BEPCⅡ的设计指标,对表1指标要求内的二极铁及四极铁误差进行了研究。表1列出了研究中二、四极铁各方向准直误差的设置范围。对于每一组状态,选一组该范围内的随机误差输入到Lattice中,用MADX模拟出带有磁铁误差的轨道,模拟调节校正磁铁强度,将每种状态下的各BPM数值和对应校正磁铁设置值储存起来。
表 1 磁铁误差设置范围Table 1. Magnet error parameters∆x/mm ∆y/mm ∆z/mm ∆θx/mrad ∆θy/mrad ∆θz/mrad dipole 0.10 0.10 0.10 0.10 0.10 0.05 quadrupole 0.10 0.10 0.25 0.25 0.25 0.10 BEPCⅡ为双环结构,本文将以BEPCⅡ电子环垂直方向的研究结果为例进行展示。BEPCⅡ电子环由一区外环、二区内环、三区内环、四区外环四个部分组成,总共使用了66个BPM和33个垂直校正磁铁。在模拟验证中共产生了500组具有磁铁误差分布下的BPM数值和对应的垂直校正磁铁数值作为数据集,数据集被划分350组为训练集和150组为测试集。表2列出了数据的分布。
表 2 数据集参数Table 2. Data set parametersfeatures numbers train data test data total data BPM 66 350 150 500 corrector 33 350 150 500 对于真实数据,用基于Python的取数清洗程序从Archiver存档系统取出对应的BPM和校正磁铁的数据并进行清洗和合并构建一个用来机器学习的数据集[9]。数据清洗主要包括不同系统数据的合并、时间戳的对齐、异常值的删除与补充等,这些操作保证了数据之间正确的对应关系。
4. 岭回归模型与L2范数正则化
机器学习特别适用于寻找不同特征之间隐藏关系的问题。轨道校正问题实际上可以是一个寻找特定磁铁误差下达到期望的束流轨道需要什么样的校正磁铁设定值的问题,这是一类回归问题。基于数据的特点,研究中采用了岭回归算法去解决此类问题。
将训练数据集350组66个BPM数据作为输入特征X,对应的33个校正磁铁设定值作为输出值Y,考虑到模型的重构性和在迁移新的场景的再利用,在保证模型精度的情况下未对数据进行标准化操作。创建一个岭回归模型,对模型进行训练来对33个校正磁铁设定值进行预测。
模型损失函数为
J(β)=∑(y−Xβ)2+λ‖β‖22 (4) 式中:第一项为预测值与真实值误差的平方和,第二项为回归系数的L2范数惩罚项。进行展开有
J(β)=∑(y−Xβ)2+∑λβ2=(y−Xβ)T(y−Xβ)+λβTβ=yTy−yTXβ−βTXTy+βTXTXβ+λβTβ (5) 若令
∂J(β)/∂β=0 ,则有{0−XTy−XTy+2XTXβ+2λβ=0β=(XTX+λI)−1XTy (6) L2范数惩罚项的加入使得
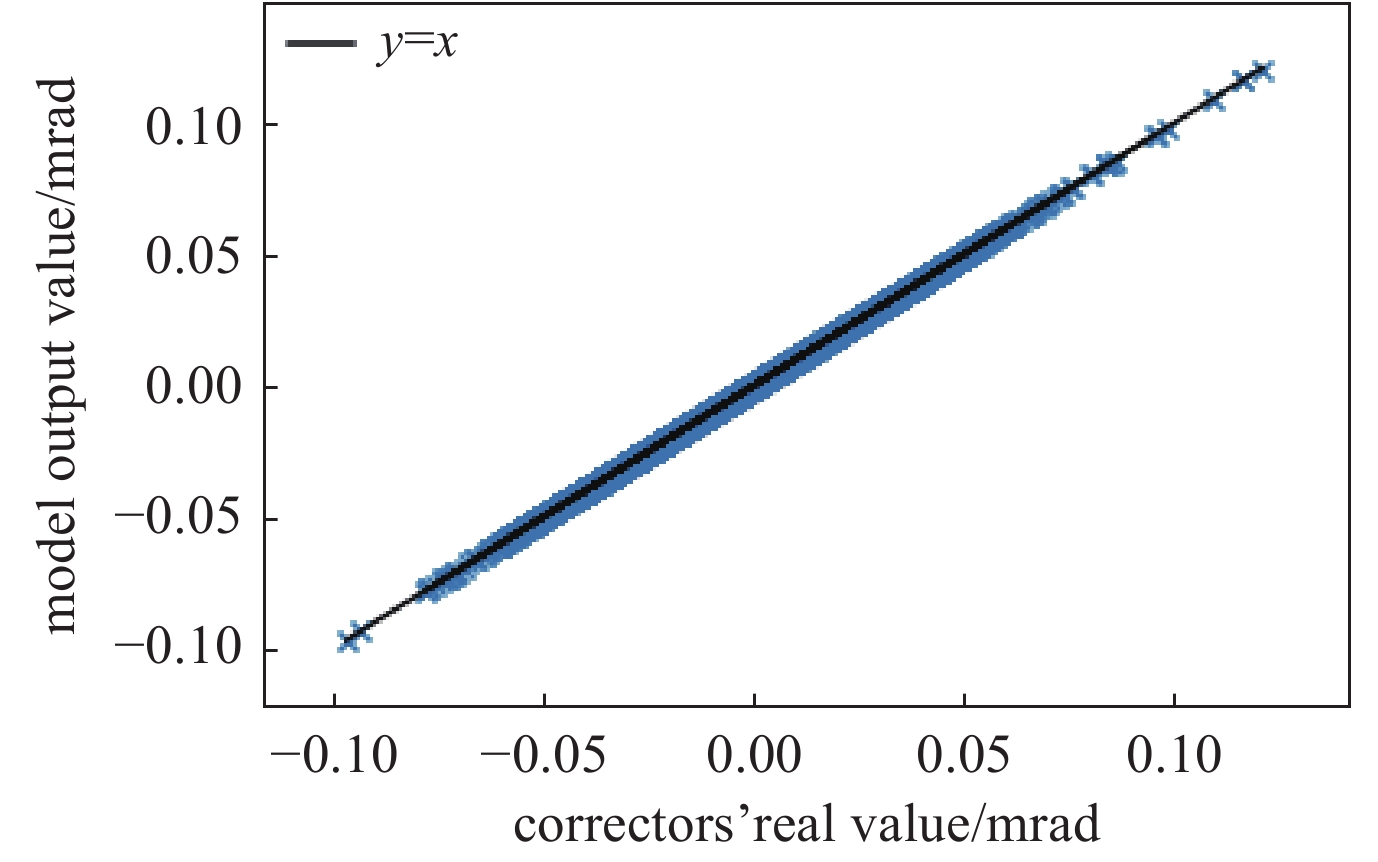
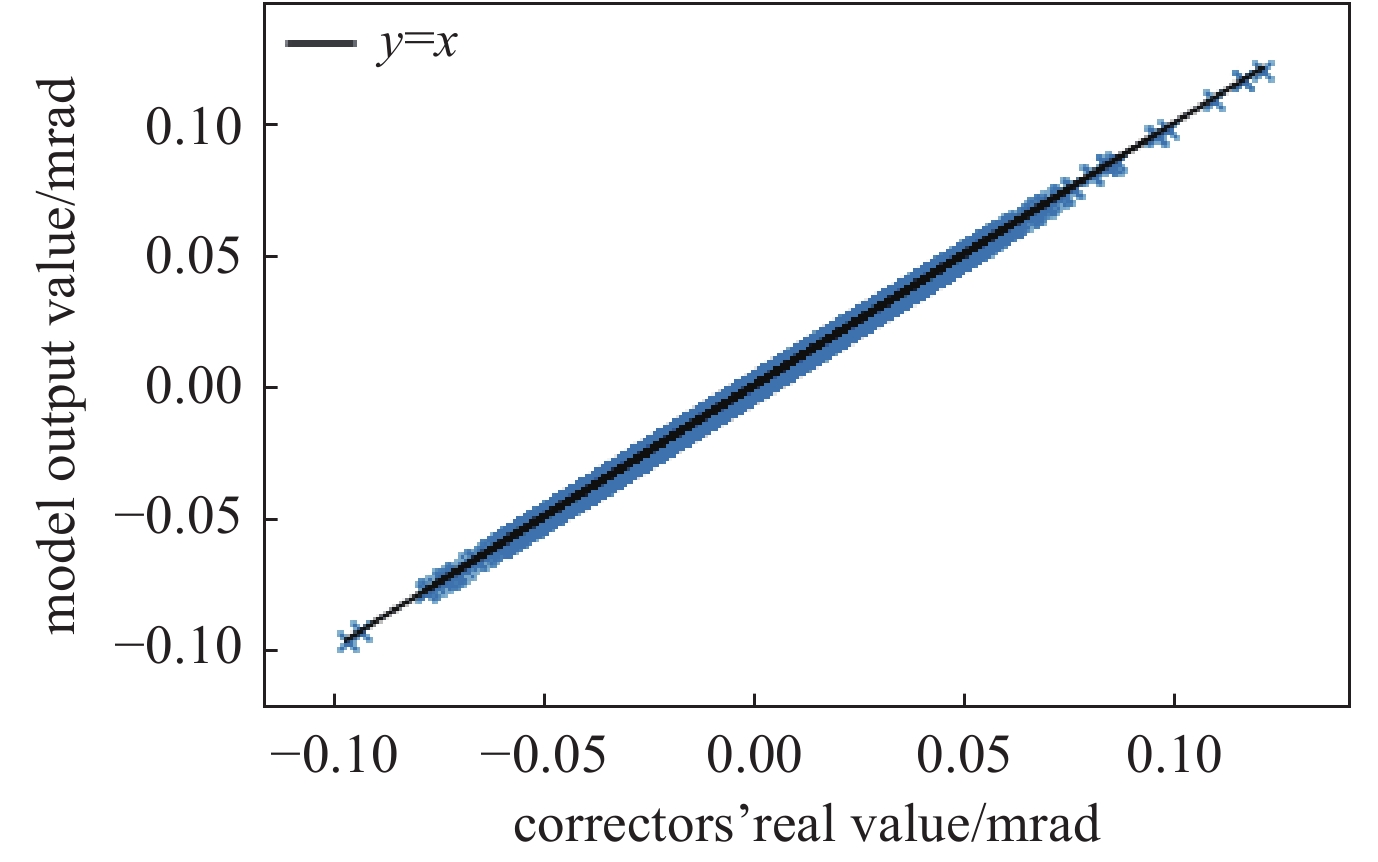
(XTX+λI) 满秩,保证了可逆性,解决了系数矩阵秩亏的病态问题[10]。对于多个BPM之间存在多重共线性,L2范数可以有效对系数起到抑制作用[11-12]。同时L2范数在保证精度的同时使系数最小化,使得校正铁强度趋向于取最小的组合,使校正磁铁尽量不超过设置限度。通过最小化损失函数,得到最佳的拟合模型。在模拟实验中,得到模型精度为99.9996%,模型MSE值(均方误差)为2.05×10−9 mrad2,RMSE值(均方根误差)为4.53×10−5 mrad。利用测试数据集对模型进行交叉验证,对测试数据集预测结果和真实结果进行比对,其精度为99.9995%,MSE值为2.52×10−9 mrad2,RMSE值为5.03×10−5 mrad,图1为测试数据集中模型输出校正铁强度值和真实值的比对关系,可以看到输出值与真实值基本全部吻合。考虑到校正磁铁的变化值在10−2 mrad量级,比模型训练标准差及测试标准差大103个量级,可以认为在误差范围内,模型对此问题进行了准确的预测。在装配Intel I5 2700 的机器上其训练时间是10 ms量级,单次预测时间为1 ms量级。在相同硬件环境测试中使用MADX中SVD方法校正所用时间在1 s量级,使用岭回归模型的方法较传统SVD方法得到成倍的提升。
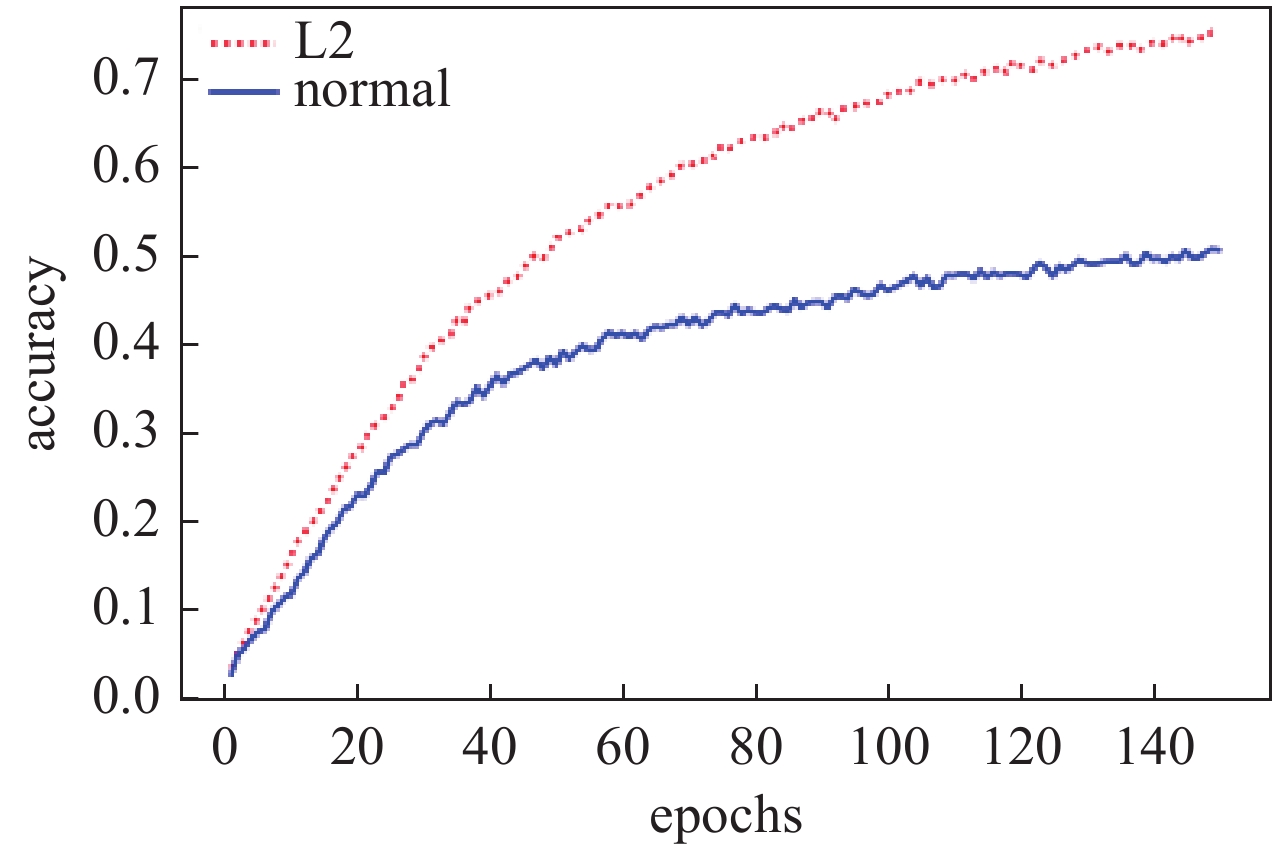
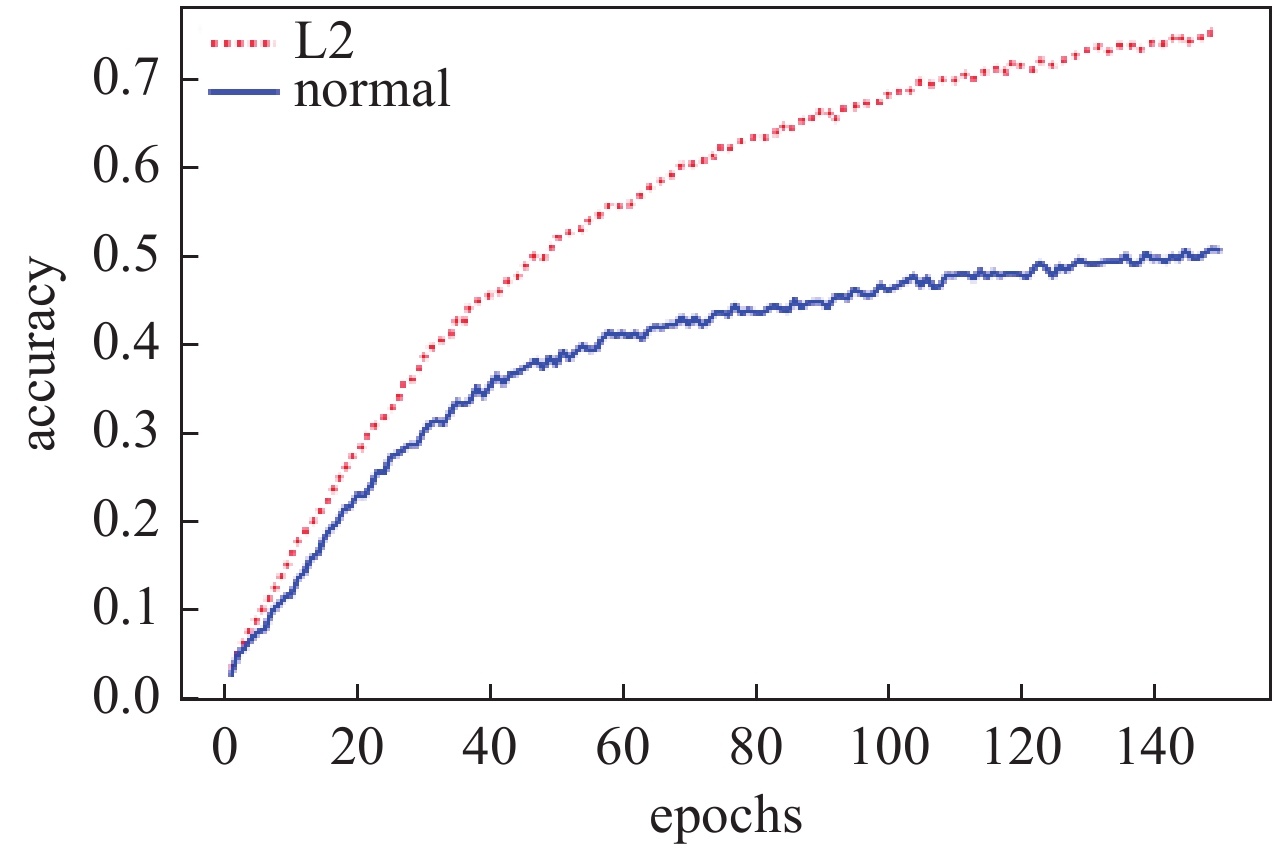
图2对比了采用L2范数正则化的有效性。通过对单层全链接神经网络进行随机梯度下降150个批次,分别对采用L2范数正则化和未采用L2范数的预测精度进行统计。结果表明,如图2所示在训练相同批次内采用L2范数正则化带来了更快的精确度上升和更高的精确度。
5. 动力学模拟检验
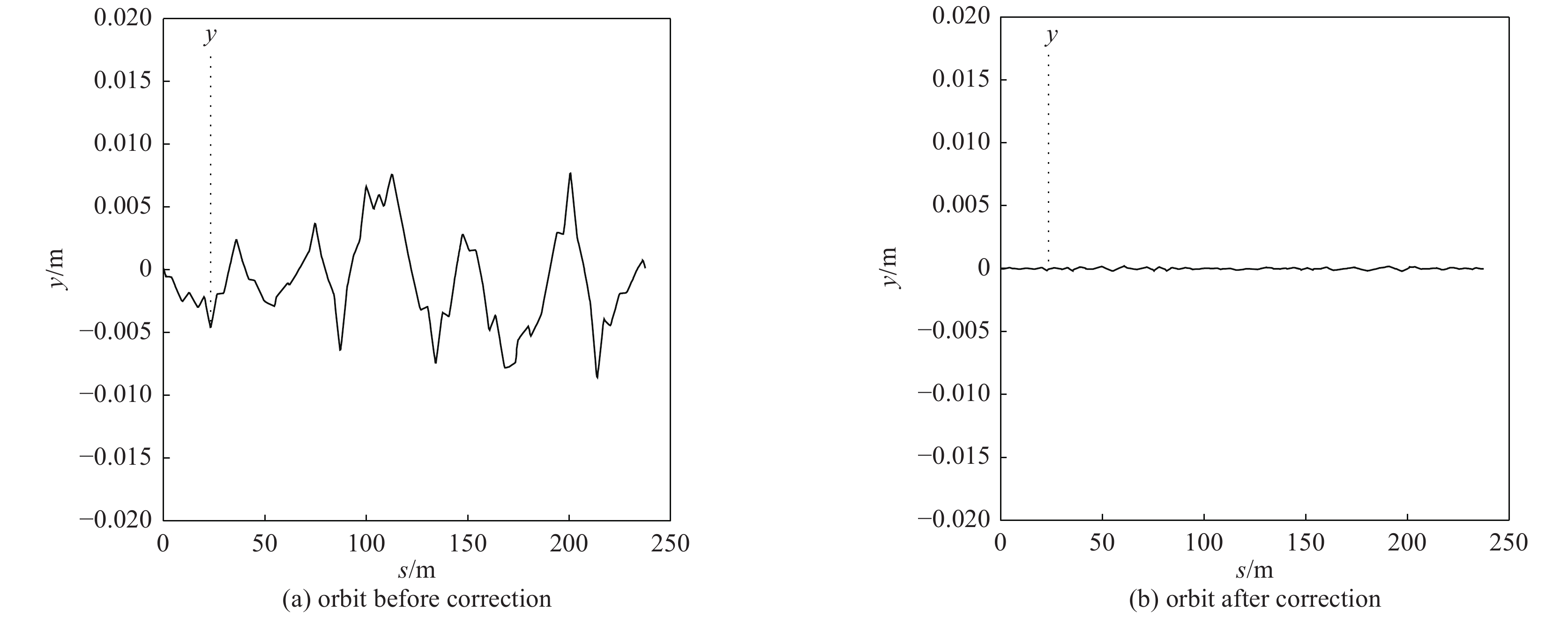
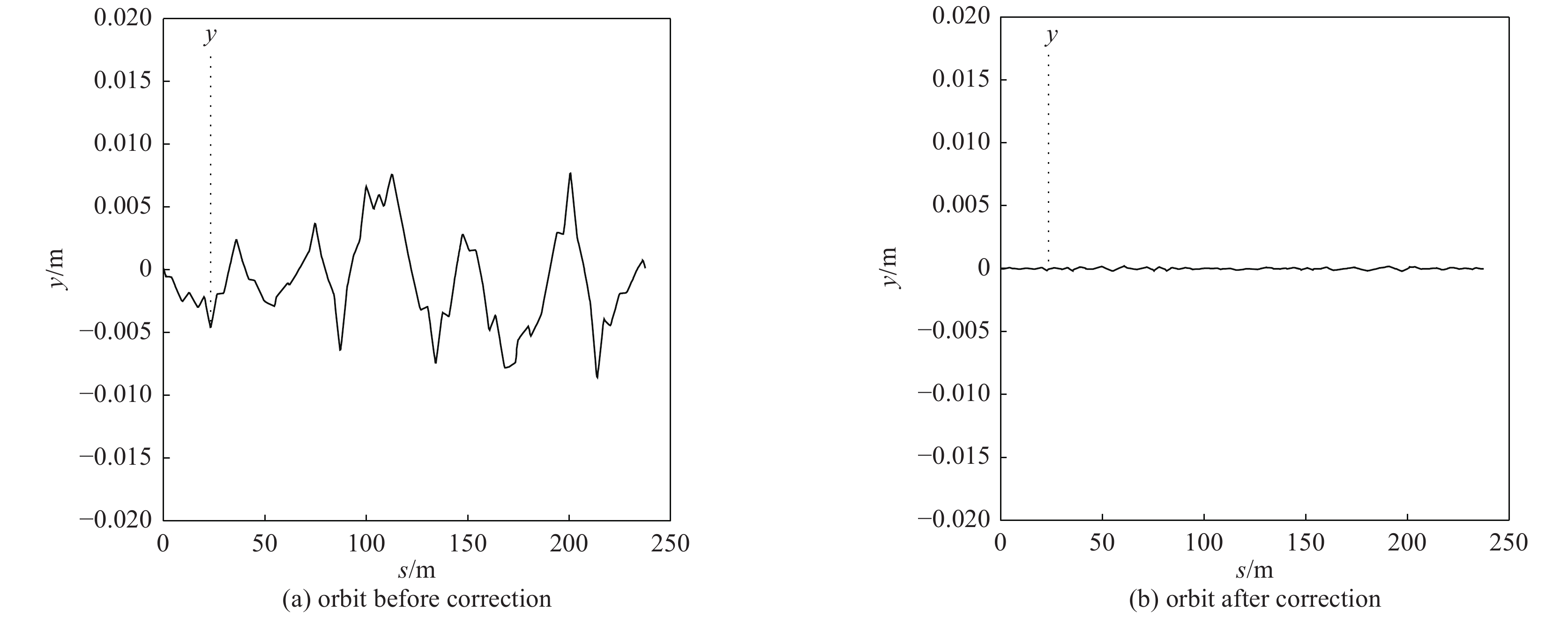
MADX是欧洲核子研究组织(CERN)开发的粒子加速器模拟及束流动力学模拟软件,已经在国际上许多粒子加速器的设计及优化中被广泛使用[3]。用MADX对引入磁铁误差的BEPCⅡ电子环Lattice进行动力学计算模拟,关闭校正磁铁以模拟轨道校正前的全环束流轨道,如图3(a)所示。将理想轨道作为期望轨道输入预先训练好的岭回归模型,得到一组模型输出的校正磁铁设置值,并将其值储存到BEPCⅡ电子环Lattice中,用MADX进行动力学模拟计算,得到校正后的全环轨道,如图3(b)所示。图3表明,模型对全环的闭轨分布进行了有效的校正。
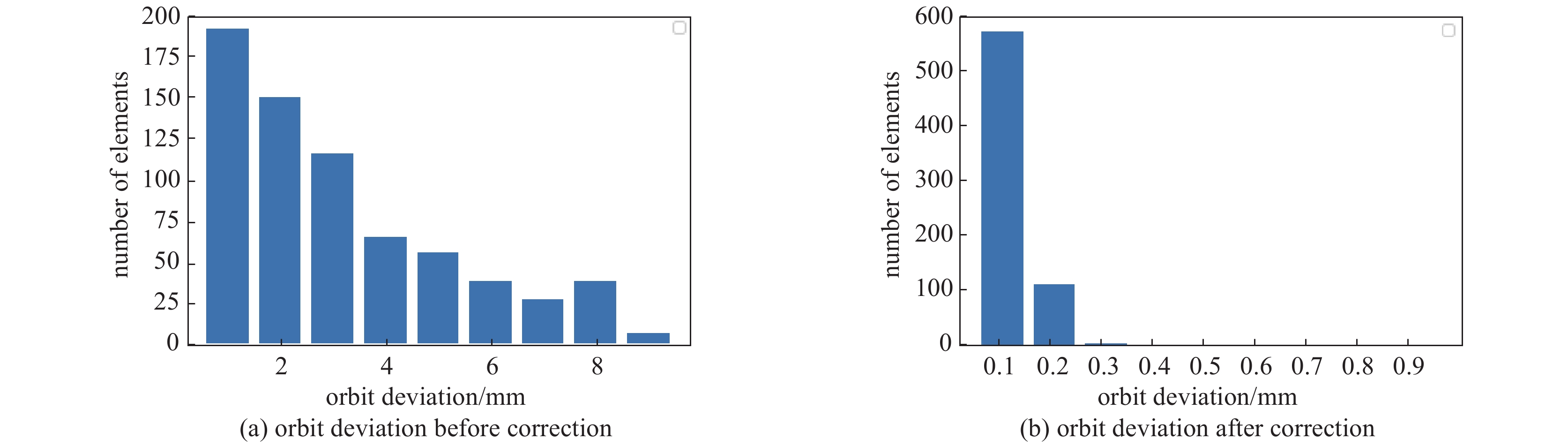
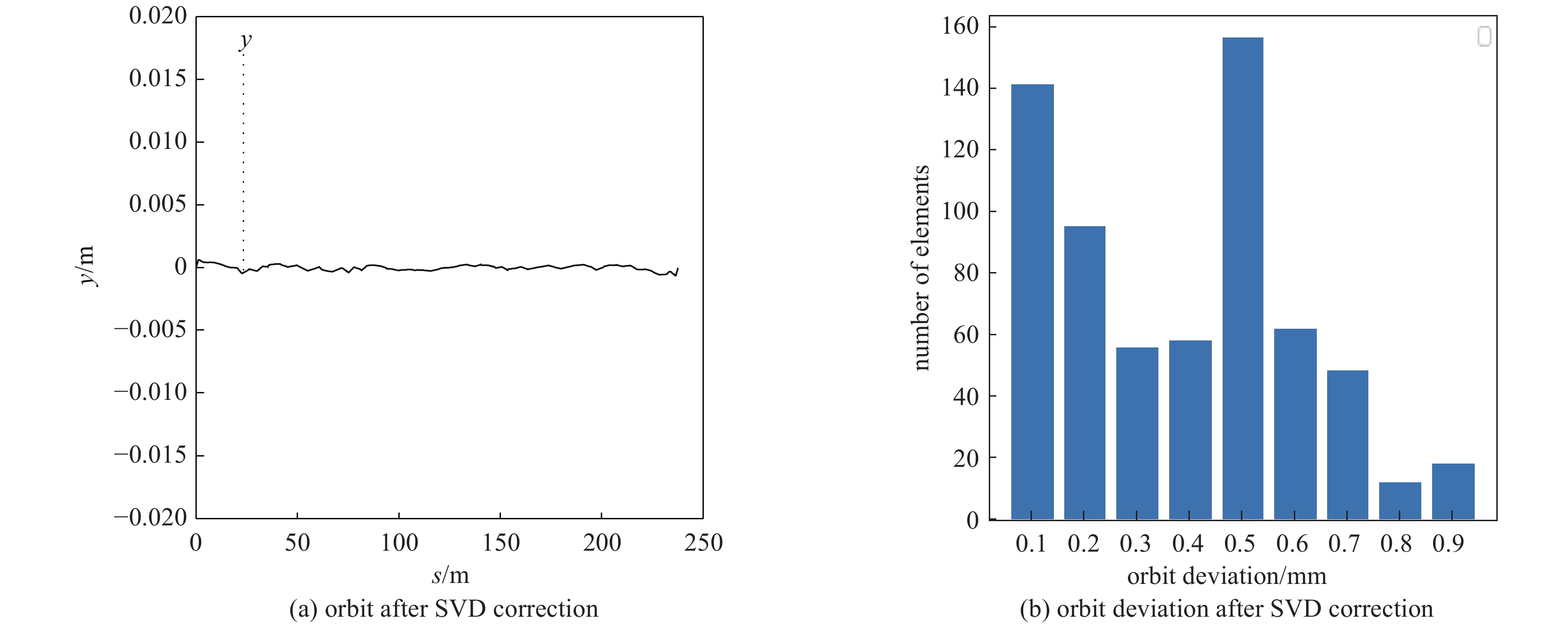
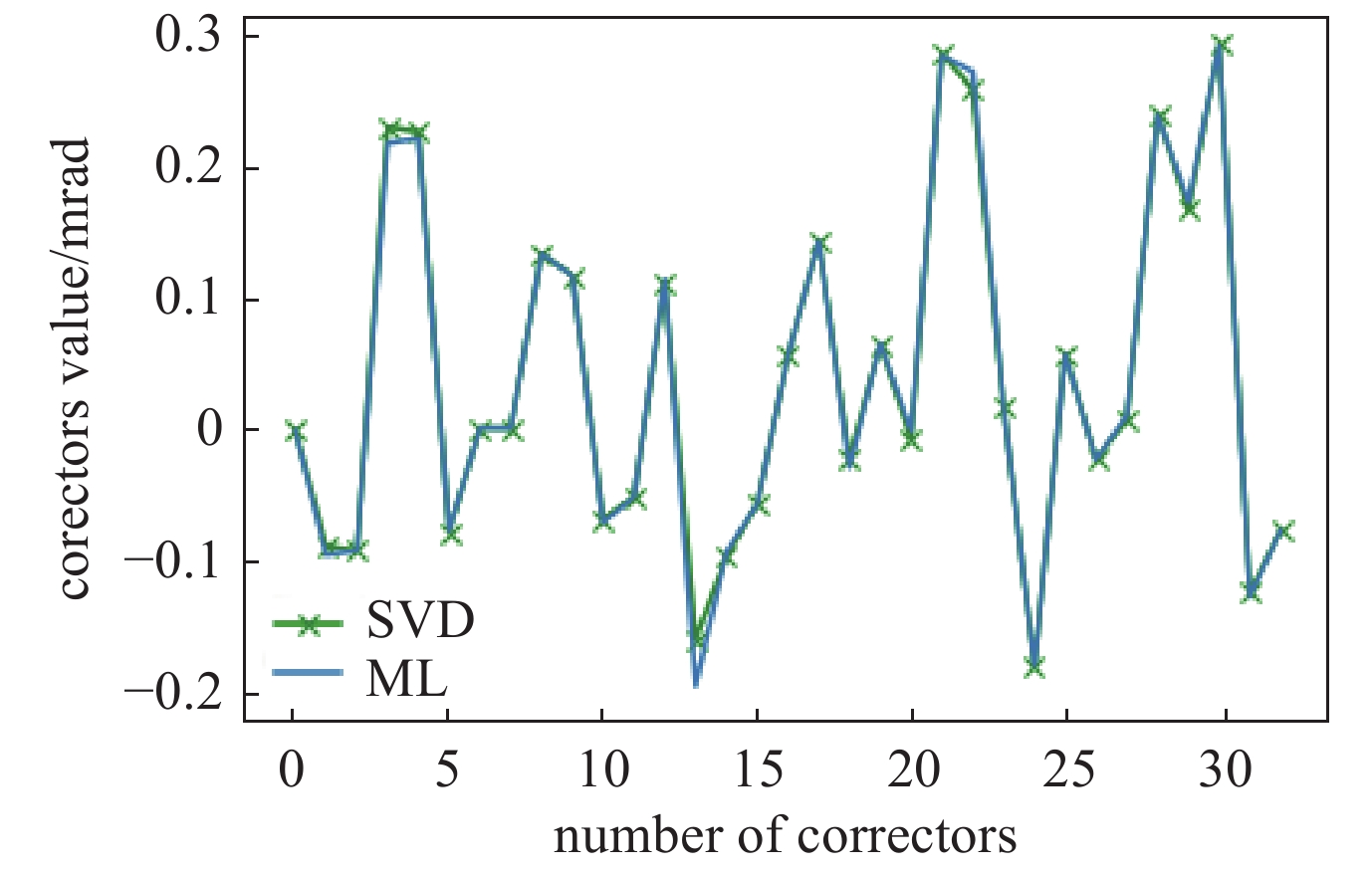
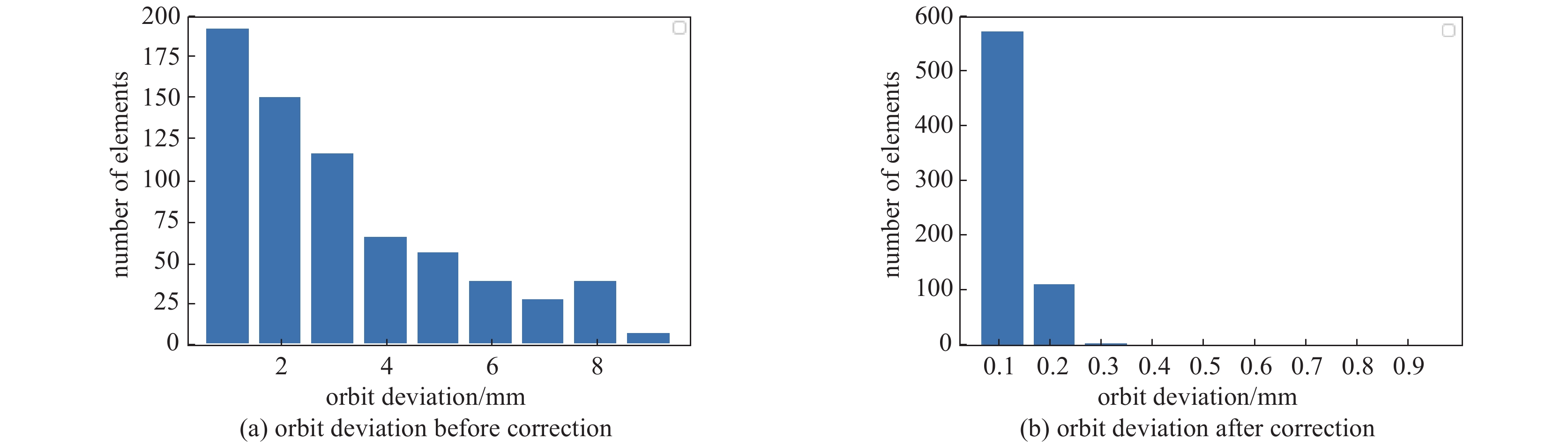
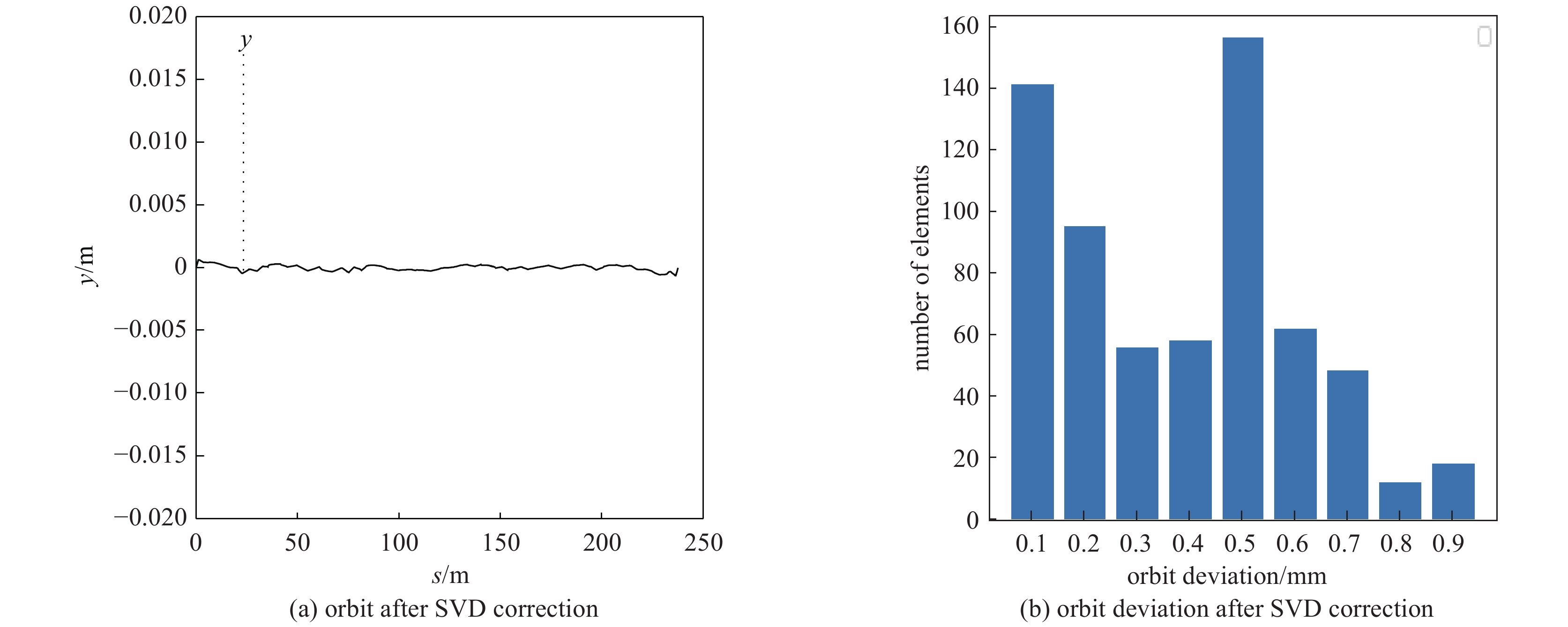
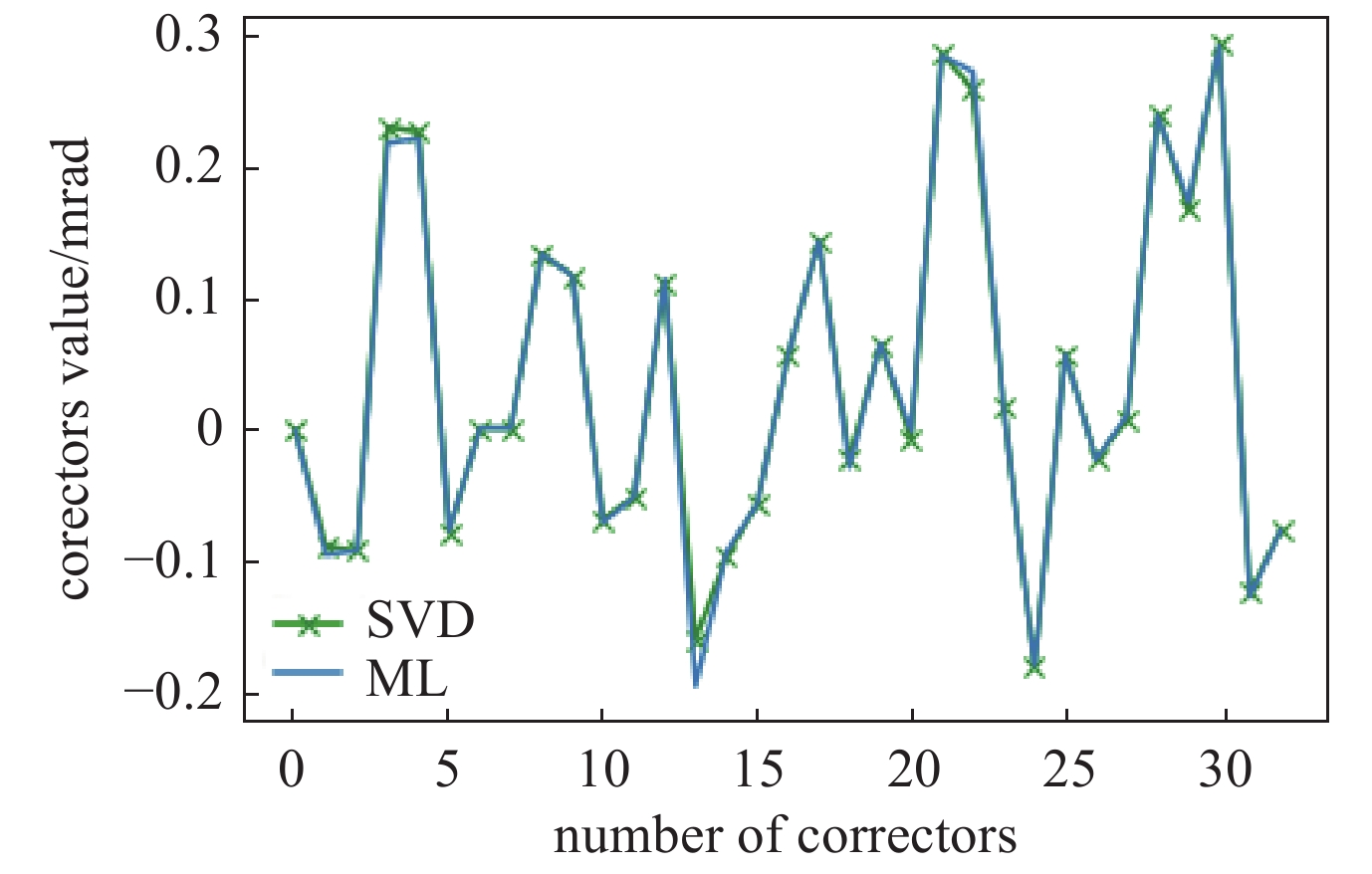
图4展示了校正前和校正后的轨道偏离统计结果。图4(a)为未进行轨道校正前原始轨道偏离理想轨道的统计,图4(b)为用模型输出值对轨道进行校正后的轨道偏离统计。如图4所示,模型将轨道的最大偏离从8 mm校正到0.2 mm范围内。图3、图4结果表明,该模型对轨道偏离进行了有效的校正。图5展示了用SVD方法校正后的轨道和轨道偏离统计,可以看出,在测试中机器学习方法校正效果不弱于SVD方法的校正效果。图6展示了机器学习方法和SVD方法校正磁铁强度的比较,结果表明,机器学习方法校正中使用的校正磁铁强度与SVD方法中校正磁铁强度相当,未对校正磁铁强度有极大的要求。
6. 真实数据检验
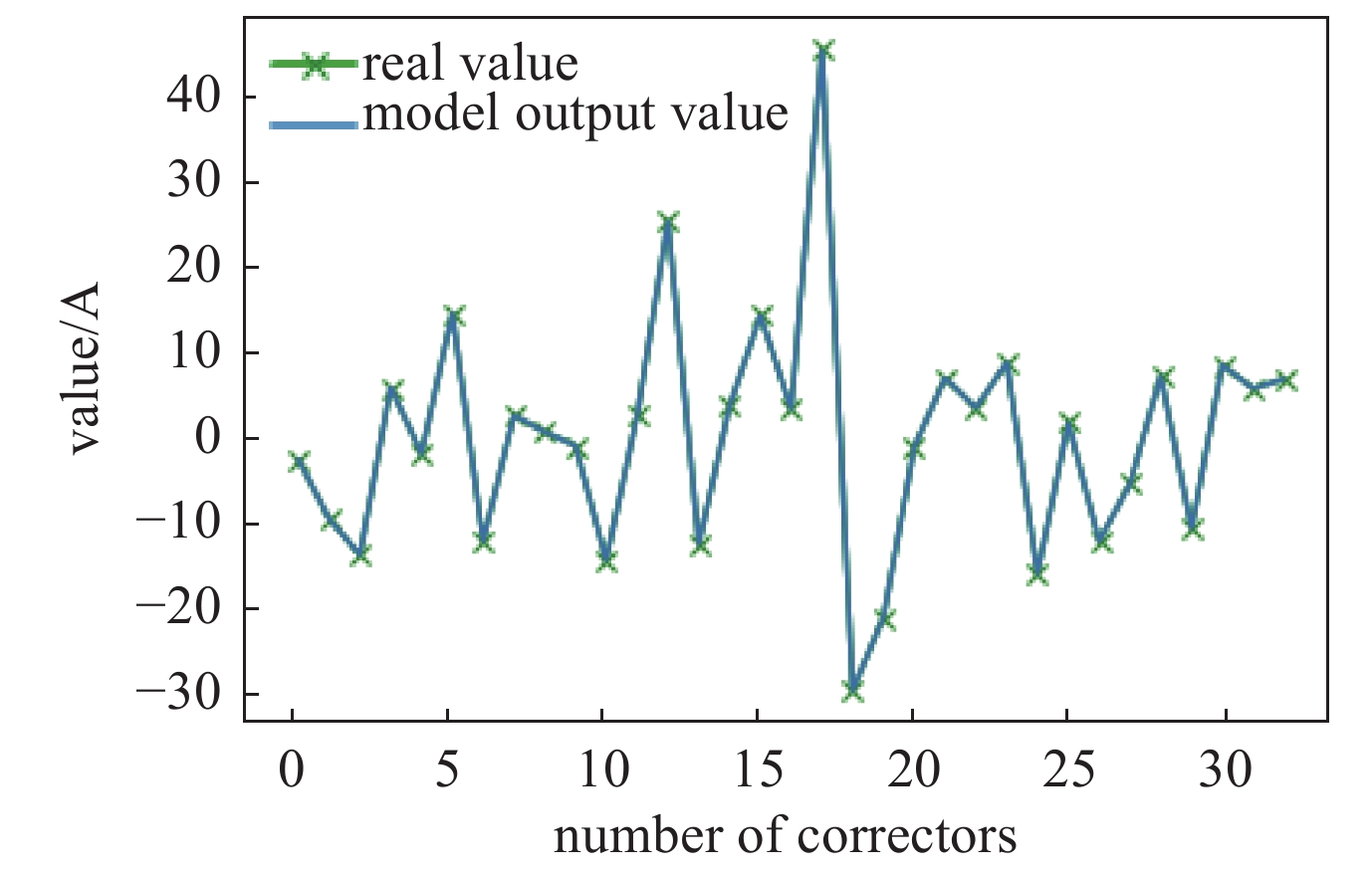
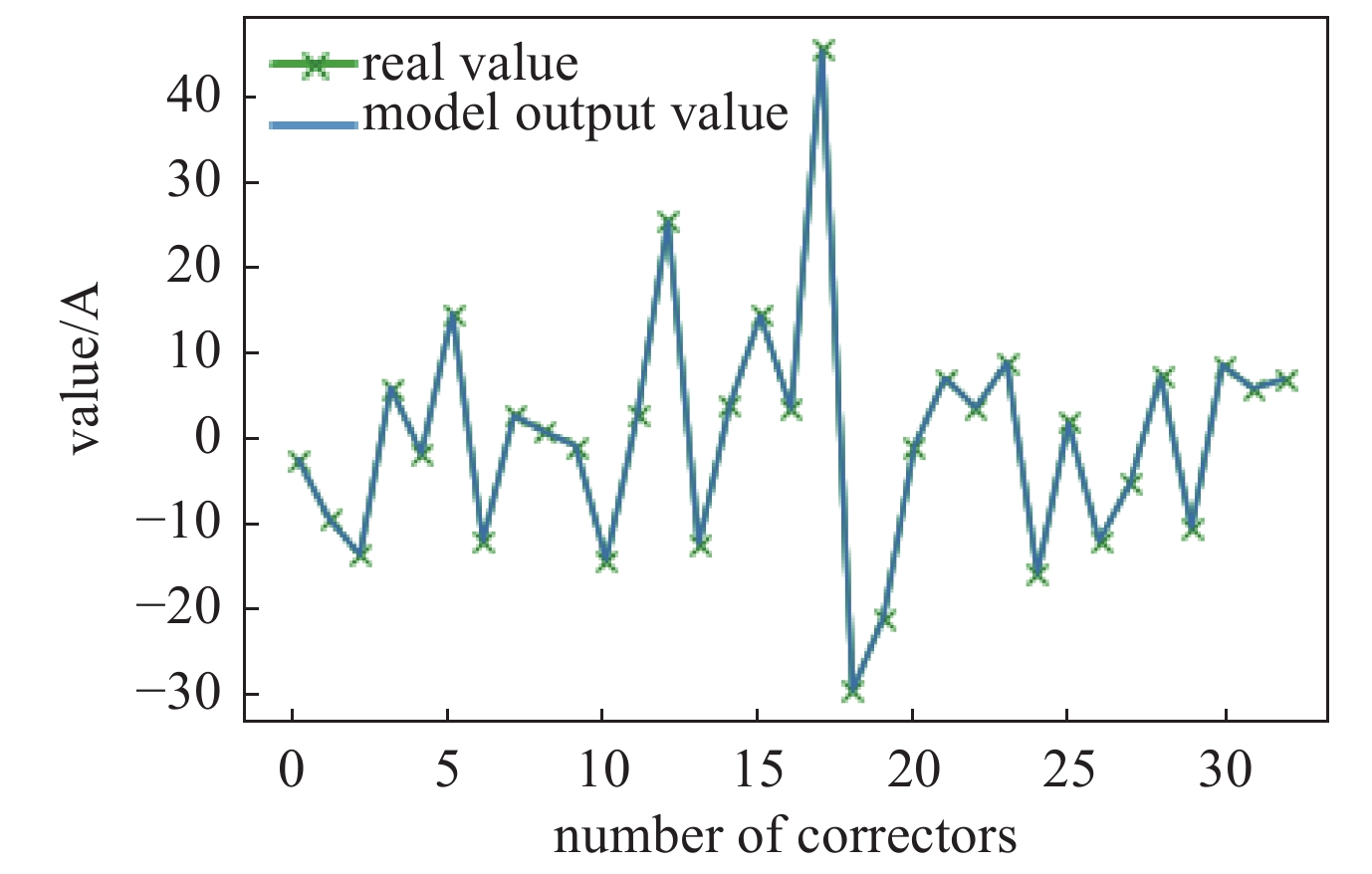
通过模拟仿真检验可以看出,该模型得到了很好的效果。为了进一步对该模型进行验证,采集BEPCⅡ电子环上的数据对该方法进行了检验。选取了2020年11月9日轨道及校正磁铁波动较大的时段进行了研究,读取了当日前50 min电子环上所有的垂直校正磁铁电流设定值、BPM束流垂直位置等数据对模型进行了训练。读取了训练数据时段10 min后的数据对模型进行检验。图7为应用该模型计算出的校正磁铁设置值和真实数值的对比,结果表明,模型计算出的校正磁铁电流设定值与真实校正磁铁电流设定值基本一致。
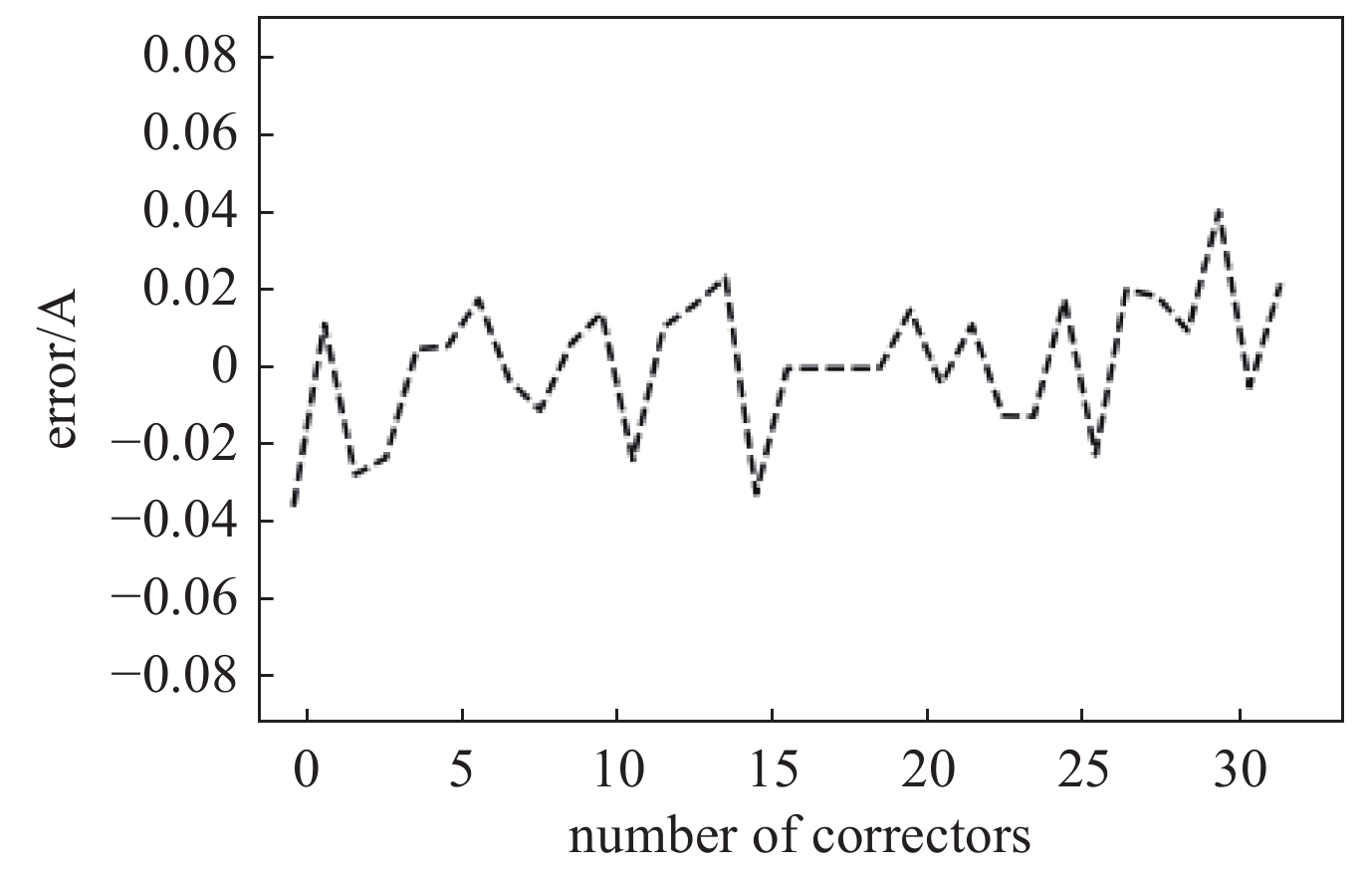
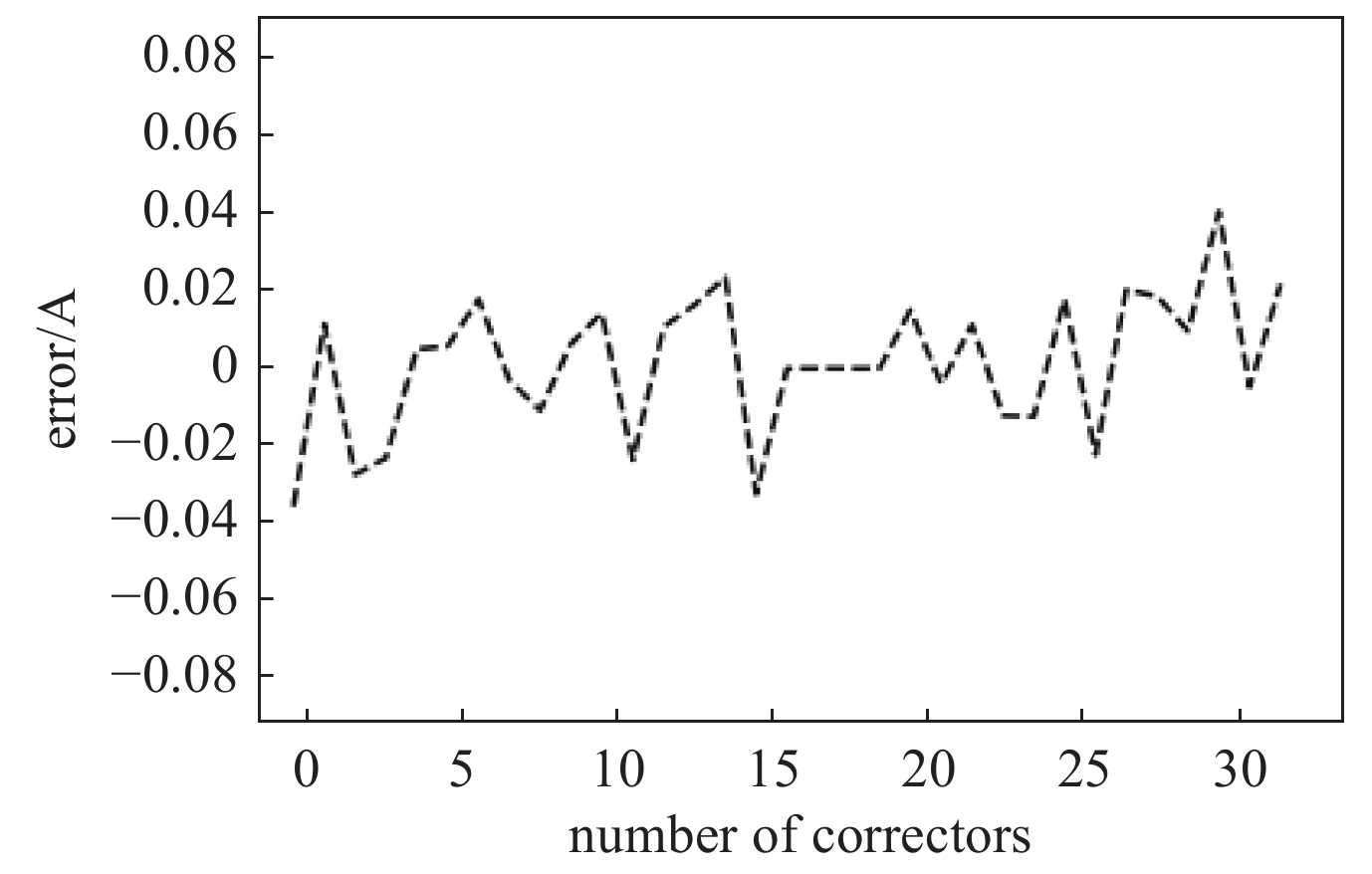
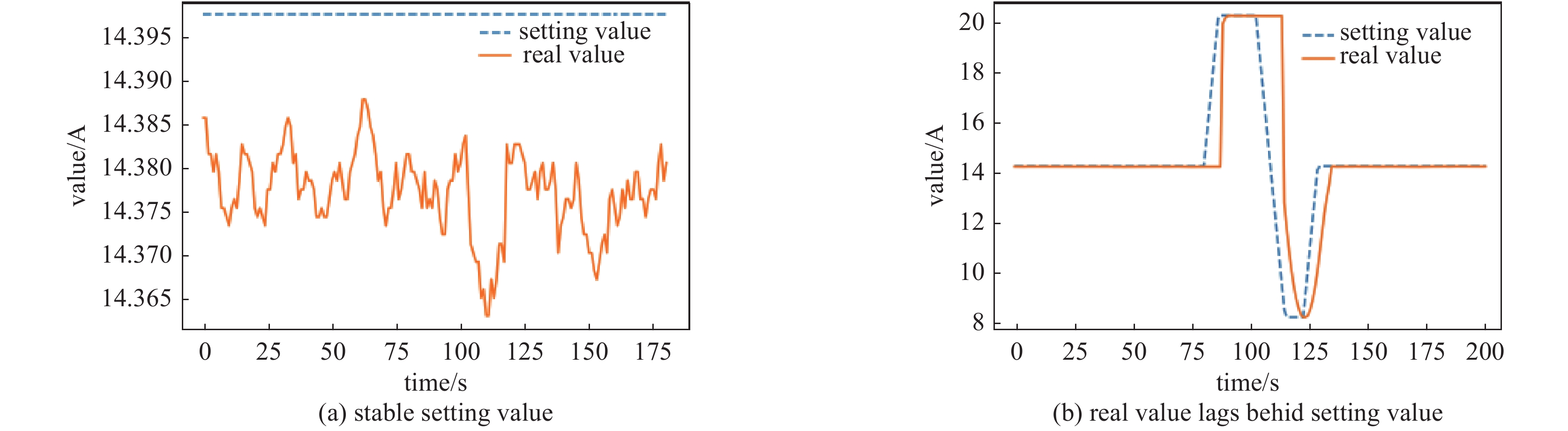
图8为模型计算出校正磁铁电流设置值与真实值之间的误差,最大误差基本在0.04 A以内。而如图9所示校正磁铁的电流设置值最大达到40 A以上,考虑到校正磁铁电流设定值与电流真实值之间的差异、校正磁铁电流真实值的波动以及校正磁铁电流真实值与设定值的滞后效应,可以认为,在数据本身所带来的误差范围内,模型对轨道校正要求的校正磁铁设置值进行了有效的计算。图9(a)展示了一段设定值稳定不变时真实值的波动变化情况,图9(b)展示了数据中校正磁铁电流真实值相对于电流设定值滞后的情况。图9表明,在实际运行中校正磁铁的真实值与设定值存在一定的误差,使得BPM处轨道响应的校正磁铁强度与设定值有些偏差。因此在机器学习模型训练的过程中,由于机器学习模型的参数是完全基于数据确定的,校正磁铁及BPM的数据噪声干扰被带入模型对计算的结果产生了影响,使得计算结果产生了一定的误差。
7. 结 论
本文介绍了一种基于机器学习的新型轨道校正方法。通过以目标轨道BPM数据作为模型输入,将轨道设定值作为模型输出,对广义矩阵进行拟合,并引入了L2范数正则化解决矩阵奇异性问题。在模拟仿真和真实数据中对该方法进行了验证,得到了一致的结果。在MADX模拟校正中,模型有效的将轨道偏差从8 mm量级校正到0.2 mm量级,并且计算时间相较传统算法SVD需要1 s量级压缩到了10 ms量级。在BEPCⅡ电子环的验证中,在误差范围内对校正磁铁设置值进行了准确的预测,达到了预期目标。同时机器学习方法作为一种以数据作为接口的方法,其易扩展性和多目标优化优势已在许多工程上应用展现出来,相较于传统方法,该方法在达到相同性能的同时,将具有更高的可扩展性。
结合该方法的垂直、水平方向轨道同时校正以及垂直、水平耦合调节将在下一步的工作中进行。同时基于数据驱动的控制系统还不够完善,且磁铁等各设备也无法在完全理想的设定值下运行,在数据收集和清洗过程中从数据本身带来了一些误差,传递到模型的误差中。开发相应的控制流程以及更好的数据收集清洗方法,将模型部署到机器上进行进一步的研究也将在接下来的工作中完成。
致 谢 感谢高能所加速器中心邢军、季大恒等所有运行组的老师在BEPCⅡ储存环及直线加速器运行值班和培训中给予的指导和帮助。感谢物理组段哲、夏文昊在模拟研究初期给予的帮助。感谢孙元胜的有益讨论。感谢高能所加速器中心控制组所有老师的有益帮助和建议。
-
表 1 磁铁误差设置范围
Table 1. Magnet error parameters
∆x/mm ∆y/mm ∆z/mm ∆θx/mrad ∆θy/mrad ∆θz/mrad dipole 0.10 0.10 0.10 0.10 0.10 0.05 quadrupole 0.10 0.10 0.25 0.25 0.25 0.10 表 2 数据集参数
Table 2. Data set parameters
features numbers train data test data total data BPM 66 350 150 500 corrector 33 350 150 500 -
[1] Hou Jie, Liu Guiming. Transport line orbit distortion correction based on response matrix and SVD algorithm[J]. High Energy Physics and Nuclear Physics-Chinese Edition, 2006, 30: 37-39. [2] Chung Y, Decker G, Evans K. Closed orbit correction using singular value decomposition of the response matrix[C]//Proceedings of 1993 IEEE Particle Accelerator Conference. 1993: 2263-2265. [3] Grote H, Iselin F C, Keil E, et al. The MAD program[C]//Particle Accelerator Conference. 1989. [4] Chu Zhongming, Xiao Dengjie, Qiao Yusi, et al. Machine learning applications for particle accelerators[J]. Frontiers of Data and Computing, 2019, 1(2): 110-120. [5] 魏源源. BEPCⅡ储存环基于响应矩阵的束流参数校正[D]. 北京: 中国科学院研究生院, 2007: 30-36.Wei Yuanyuan. Optics correction using response matrix at BEPCⅡ storage rings[D]. Beijing: Institute of High Energy Physics, Chinese Academy of Sciences, 2007: 30-36 [6] 刘渭滨. BEPCⅡ直线加速器束流光学轨道校正程序设计[D]. 北京: 中国科学院研究生院, 2004: 13-17.Liu Weibin. BEPCⅡ Linac optics calculations and orbit correction program design[D]. Beijing: Institute of High Energy Physics, Chinese Academy of Sciences, 2004: 13-17 [7] Xiao Dengjie, Chu Zhongming, Qiao Yusi. Orbit correction with machine learning[C]//Proceedings of the 10th International Particle Accelerator Conference. 2019: 2608-2610. [8] Bai Sha, Gao Jie, Geng Huiping. Orbit correction in CEPC[C]//Proceedings of the 6th International Particle Accelerator Conference. 2015: 2022-2024. [9] 乔予思. 大型加速器数据存储查询和处理的软件技术研究[D]. 北京: 中国科学院大学, 2019: 89-109.Qiao Yusi. Study of large particle accelerator’s data archiving, retrieving and processing software technology[D]. Beijing: University of Chinese Academy of Sciences, 2019: 89-109 [10] Mcdonald G C. Ridge regression[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 1: 93-100. [11] 杨楠. 岭回归分析在解决多重共线性问题中的独特作用[J]. 统计与决策, 2004(3):14-15. (Yang Nan. Ridge regression for nonorthogonal problems[J]. Statistics and Decision, 2004(3): 14-15 doi: 10.3969/j.issn.1002-6487.2004.03.007 [12] Hoerl A E, Kennard R W. Ridge regression: biased estimation for nonorthogonal problems[J]. Technometrics, 2012(12): 55-67. 期刊类型引用(1)
1. 侯明阳,郭玉辉,杨旭辉,杨贵进. 基于边缘加速节点的直线加速器束流轨道参数预测技术研究. 原子核物理评论. 2024(04): 975-983 .  百度学术
百度学术其他类型引用(5)
-





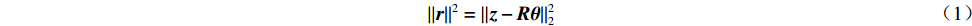
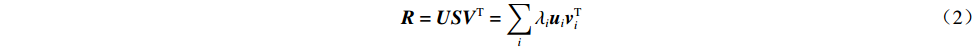

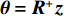
 下载:
下载:

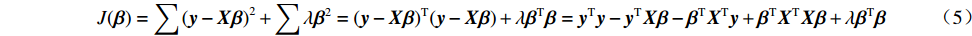
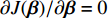
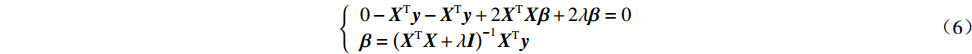
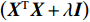









 下载:
下载: