近年来，随着计算机以及相关学科技术的发展，基于机器视觉的测量技术越来越受到关注。双目视觉测量技术因其设备简单、成本低、非接触测量、操作方便，以及具有实时、在线测量的潜力，广泛应用于工业生产、物体识别、工件测量、机器人自动导航、无人驾驶和航天等多个领域^[1]。

影响双目视觉系统的测量精度因素有：特征点的提取与匹配、摄像机标定误差以及系统结构参数的选取^[2]。在相机标定、目标识别、特征点提取、立体匹配等方面得到了较为充分的研究，而系统结构参数对测量精度影响的研究则比较少。大多机器视觉系统的搭建是靠人为经验来选择的，可以参考的资料很少。例如：闵新力等人首次在理论上系统、详尽地分析了系统结构参数与系统误差之间的关系，并通过实验对结论进行了验证^[3]；赵萍等人给出了在设计双目视觉系统时，光轴的夹角应该在20°～45°，基线距离应该在300～500 mm的结论^[4]；肖志涛等人从理论上分析了摄像机标定、镜头参数以及系统结构参数对双目视觉测量系统的影响，并用实验验证了理论分析的准确性^[5]；Yu Huan等人通过Matlab软件仿真，分析了平行双目立体视觉系统的水平视角、基线距离、透镜焦距等结构参数对测量误差的影响，并且得到了每个参数在特定范围内的测量误差最小^[6]；Lu Yang等人综合地分析了系统结构参数和摄像机标定参数对于双目视觉系统定位精度的影响^[7]；毕超等人通过公式推导得到了基线间距、相机焦距、物距和像素误差等结构参数与测量误差的表达式，并且分析了这些参数与测量误差的关系和影响^[8]；国外也有学者对此展开研究，Fahimeh Fooladgar等人通过仿真分析了基线长度、焦距和像素大小等参数对误差的影响^[9]；Kristiaan Schreve等人探讨了摄像机各参数的不确定性以及量化不确定性的影响，并提出了精度模型，有利于双目立体相机的结构设计^[10]；Zhang Tao等人提出了一个更为通用的误差模型，最大限度地减少重建误差，提高了双目系统的测量精度^[11]；Stefan Wenhardt等人建立了立体相机系统的参数与给定曲面三维重建误差之间的数学关系^[12]。

这些研究主要是根据双目立体视觉系统的数学模型从理论和仿真上来分析各种参数对测量误差的影响，并没有从真正意义上去仿真双目成像的过程。由于透镜的尺寸一方面直接影响着成像分辨率，另一方面又影响着系统的结构和景深。因此根据应用需要，兼顾系统结构、成像分辨率以及系统的景深合理选择成像系统的接收口径尺寸至关重要^[13]。

本文首先利用非相干成像的理论对双目视觉的成像过程进行了仿真和实验；其次通过加速鲁棒特征（SURF）算法来提取所采集的左右图像的特征点，并且对其进行特征点匹配，从而获取匹配点的坐标值，进而计算出左右两幅图像的视差均方根误差来表征系统的测量误差；最后通过改变透镜孔径大小在不同匹配点数目的条件下得出了透镜孔径与系统的测量误差之间的关系。

1.   研究方法

1.1   非相干成像

假如1个物函数为${U_0}\left ( {{x_0},{y_0}} \right )$，当用非相干光对物面进行照明时，物面上任意点发出的脉冲，即点扩散函数都非相干，在像面上相对应的脉冲响应非相干叠加，也就是强度叠加。非相干成像系统是关于强度的线性系统。其物像关系满足以下卷积积分^[14]

式中：$C$是常数，${I_0}$是物的强度分布，${I_{{i}}}$是像强度分布，${h_{\rm{I}}}$是强度点扩散函数。物像之间的关系在频域中可以表示为^[15]

式中：${G_0}\left( {\alpha ,\beta } \right)$，${G_{i}}\left( {\alpha ,\beta } \right)$，${H_{\rm{I}}}\left( {\alpha ,\beta } \right){\kern 1pt} {\kern 1pt} {\kern 1pt}$分别是${I_0}({x_{i}},{y_{i}})$，${I_{i}}({x_{i}},{y_{i}})$，${h_{\rm{I}}}({x_{i}},{y_{i}}){\kern 1pt}$的傅里叶变换。

实际应用中在意的是携带信息的那部分光强与零频分量的比值，即${G_0}\left( {\alpha ,\beta } \right)$，${G_{\rm{i}}}\left( {\alpha ,\beta } \right)$和${H_{\rm{I}}}\left( {\alpha ,\beta } \right)$分别与零频分量的比值，引入归一化频谱，由式（2）可得

${H_{\rm{I}}}\left( {\alpha ,\beta } \right)$定义为非相干成像系统的光学传递函数^[16]（OTF），它可以用来评价非相干成像系统在频域中的效应。

1.2   SURF算法的原理

特征点的提取与匹配对于获取准确的视差值具有很大的影响，这不仅与所获得的图像有关，还与所采用的匹配算法有关。目前比较常用的方法主要有尺度不变特征（SIFT）算法 ^[17]，SURF算法^[18]和快速特征点提取和描述（ORB）算法^[19]，由于SURF算法旋转鲁棒性、模糊鲁棒性、尺度变换鲁棒性都比其他两种算法要好，而计算速度仅次于ORB算法^[20]。因此，本文采用是Herbert Bay提出的SURF算法。其基本原理可以分为以下几个步骤。

（1）构建Hessian矩阵^[21]。其目的是为了生成图像的特征点，为后续的特征提取做准备。对于图像$I\left( {x,y} \right)$，其Hessian矩阵

它的判别式为

首先需要对图像进行高斯滤波再建立Hessian矩阵，其表达式如下

式中：$\left( {x,y} \right)$为图像的像素坐标，$L\left( {x,y,\sigma } \right) = G\left( \sigma \right) I\left( {x,y} \right)$表示图像的高斯尺度空间，是通过不同的高斯核与图像卷积获得的。

利用这种方法可以计算出图像中每个像素的H行列式的判定值，通过该值来判定图像$I\left( {x,y} \right)$中的特征点。${\rm{Det}}\left( H \right)$中的$L\left( {x,y} \right)$是初始图像的高斯卷积，因为高斯核服从正态分布，系数由中心点向外逐渐减小，为了加快运算速度，SURF算法用方块滤波器代替了高斯滤波器L，所以需要给${L_{{xy}}}$赋予一个权重系数0.9，这样才能抵消方块滤波器所带来的误差，可得Hessian矩阵的判别式

（2）构造尺度空间^[22]。在SURF算法中，不同组之间的图像大小都相同，不同组之间所用的方块滤波器的模板尺寸会逐渐变大，同一组不同层图像所用的滤波器的大小一样，但是滤波器的尺度空间因子逐渐变大。

（3）特征点定位^[23]。SURF算法将经过Hessian矩阵处理后的每个像素与图像域和尺度域的全部相邻点进行比较，只要该点大于或者小于所有邻域点，则确定其为特征点。

（4）确定特征点方向^[23]。采用了Harr小波特征，在一个圆形邻域内，统计在60°扇形区域内特征点在水平方向和垂直方向的Harr小波特征总和，然后以0.2 rad的间隔旋转扇形，并且再统计其Harr小波特征值，最后将最大值的扇形方向确定为该特征点的主方向。

（5）生成特征描述子^[24]。提取特征点范围内4×4的区域，其方向沿着特征点的主方向。在每一个子区域内统计25个像素点在水平和垂直方向的Harr小波特征，其具有4个方向的特征，分别为垂直方向值之和，水平方向值之和，垂直方向绝对值之和以及水平方向绝对值之和。因此一共有4×4×4=64维的特征描述子。

（6）特征点匹配。通过2个特征点之间的欧氏距离来确定其匹配度，距离越近则其匹配度越好。除此之外，还需要通过Hessian矩阵的迹剔除误匹配点，如果2个特征点的Hessian矩阵迹具有相同的正负号，则不需要剔除，否则即使欧氏距离为零，也要剔除。

1.3   计算视差均方根误差

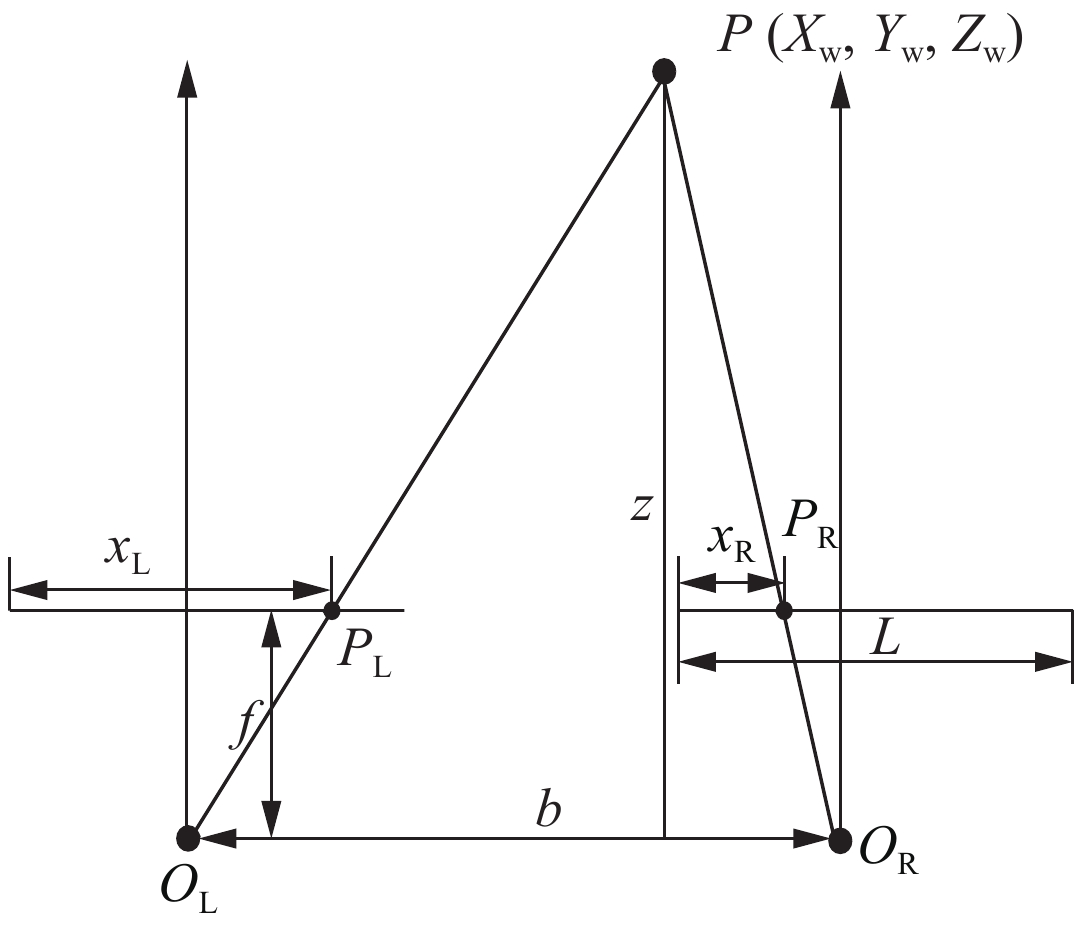
双目成像模型如图1所示，P为空间中的一点，P_L和P_R分别为点P在左右像平面上的像点，f是焦距，O_L和O_R是左右相机的光心，b为光心之间的距离（基线），${x_{\rm{L}}}$和${x_{\rm{R}}}$分别为像点P_L和P_R到成像面最左边缘的距离，其视差公式^[25]为

图  1  双目成像模型

Figure  1.  Binocular imaging model

下载: 全尺寸图片 幻灯片

根据均方根误差的公式可得计算视差均方根误差的公式为

式中：N为测试的次数，d_obs,i为视差的测试值，d_true,i为视差的真值。通过计算每一张图像对的视差均方根误差来表征系统误差。

2.   计算机模拟

首先在计算机上模拟非相干双目成像过程；然后采用SURF算法对所获得的左右图像对进行特征提取与匹配，进而计算出左右图像对的视差值；最后求得视差均方根误差来表征系统误差，分析透镜孔径大小与系统误差之间的关系。本文的仿真流程如图2所示。

图  2  仿真流程图

Figure  2.  Simulation flow chart

下载: 全尺寸图片 幻灯片

2.1   双目成像过程

分辨率板分别在左右2个相机上成像，共125组图像对，仿真所采用的物体为美国空军分辨率板，设该分辨率板的几何尺寸L_o为5 mm×5 mm，如图3所示。仿真时所设置的相关参数：波长λ=600 nm，透镜焦距f=30 mm，透镜的孔径D=0.2～28 mm。仿真时物体的采样点数目为512×512像素。

图  3  美国空军分辨率板

Figure  3.  United States Air Force resolution board

下载: 全尺寸图片 幻灯片

在非相干照明下，双目成像的主要流程如图4所示。

图  4  双目成像仿真流程图

Figure  4.  Binocular imaging simulation flow chart

下载: 全尺寸图片 幻灯片

2.2   特征点提取及匹配

由于匹配点数目达到一定的数值后，匹配点的数目对系统误差的影响不大，并且为了能够满足在一定的孔径范围内匹配到相同数量的匹配点数目，其设定不能超过最小孔径所能匹配到的匹配点数目。只有这样才可以排除匹配点数目对于系统误差的影响，保证了单一变量——孔径尺寸对系统误差的影响，因此将匹配点的数目设为25个、40个、55个、70个。

分别在设定的匹配点数目条件下采用SURF算法对双目成像仿真过程中所得到的分辨率板图像进行特征点提取与匹配，获取匹配点对的坐标，并且根据式（8）计算出匹配点的视差，根据式（9）计算出视差的均方根误差来表征系统误差。

2.3   分析仿真结果

通过计算机仿真实验，我们一共得到了4组实验数据，为了更加直观地表示透镜孔径大小与系统误差之间的关系，采用多项式拟合法将所得到的数据进行曲线拟合如图5所示，图中每条曲线分别表示在不同匹配点数目的条件下拟合的结果。

图  5  分辨率板:透镜孔径大小与系统误差之间的关系

Figure  5.  Resolution board: the relationship between lens aperture size and system error

下载: 全尺寸图片 幻灯片

由图5（a）可以看出，当匹配点的数目保持不变，即匹配点数目为25个时，随着透镜孔径的增大，系统误差持续减少，并且当透镜孔径增大到达到一定的数值时，系统误差趋近于0。图5（b）、图5（c）、图5（d）分别是在匹配点数目为40个、55个、70个的条件下透镜孔径大小与系统误差之间的关系，得到的结果与图5（a）的仿真结果一致。此外，从这4组实验数据中，我们还可以看出，当匹配点的数目增加时，系统误差的变化趋势基本保持一致。

为了保证仿真实验的准确性，本文还增加了2组仿真实验，所采用的输入图像如图6所示。

图  6  新增2张作为物的图像

Figure  6.  Two images added as objects

下载: 全尺寸图片 幻灯片

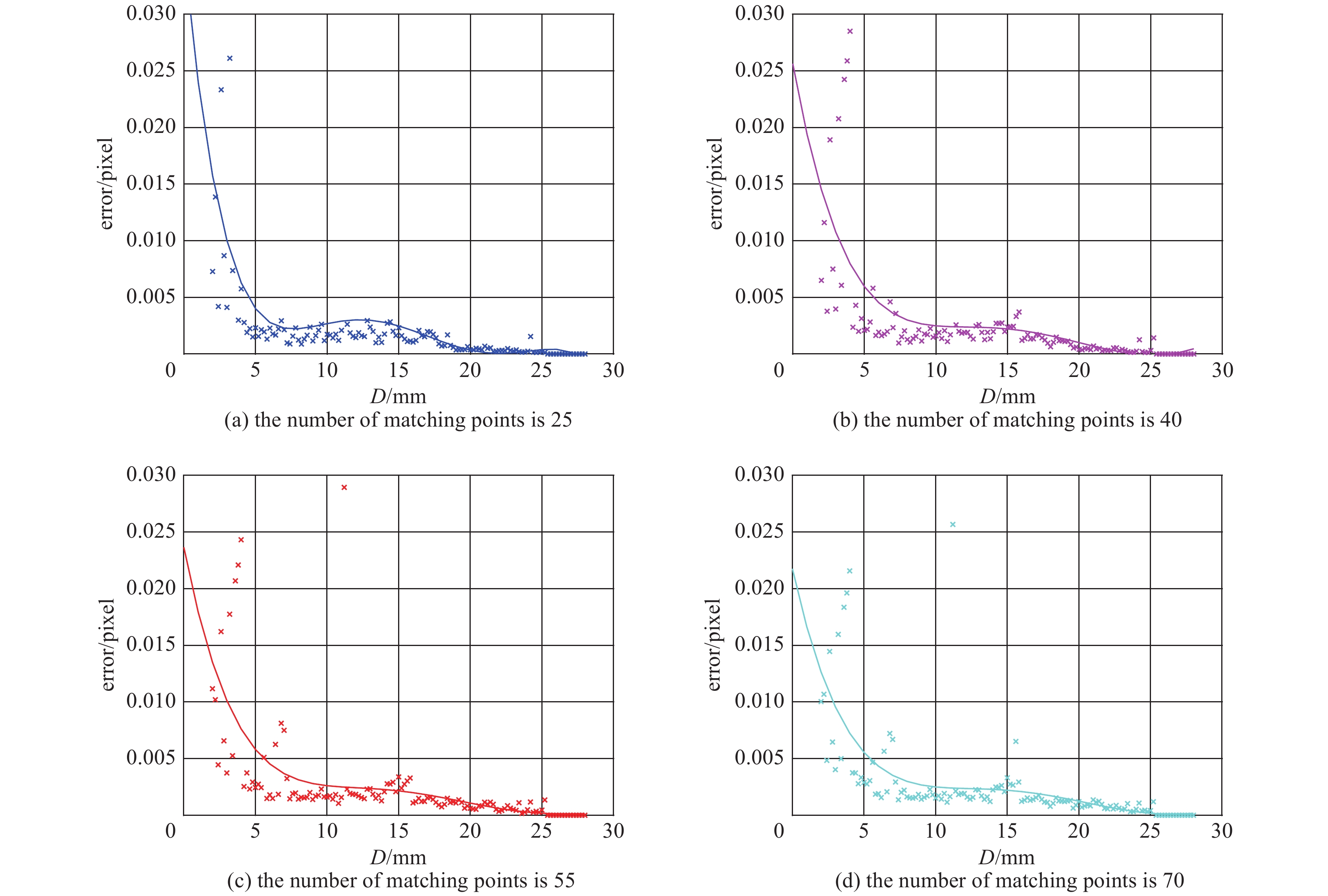
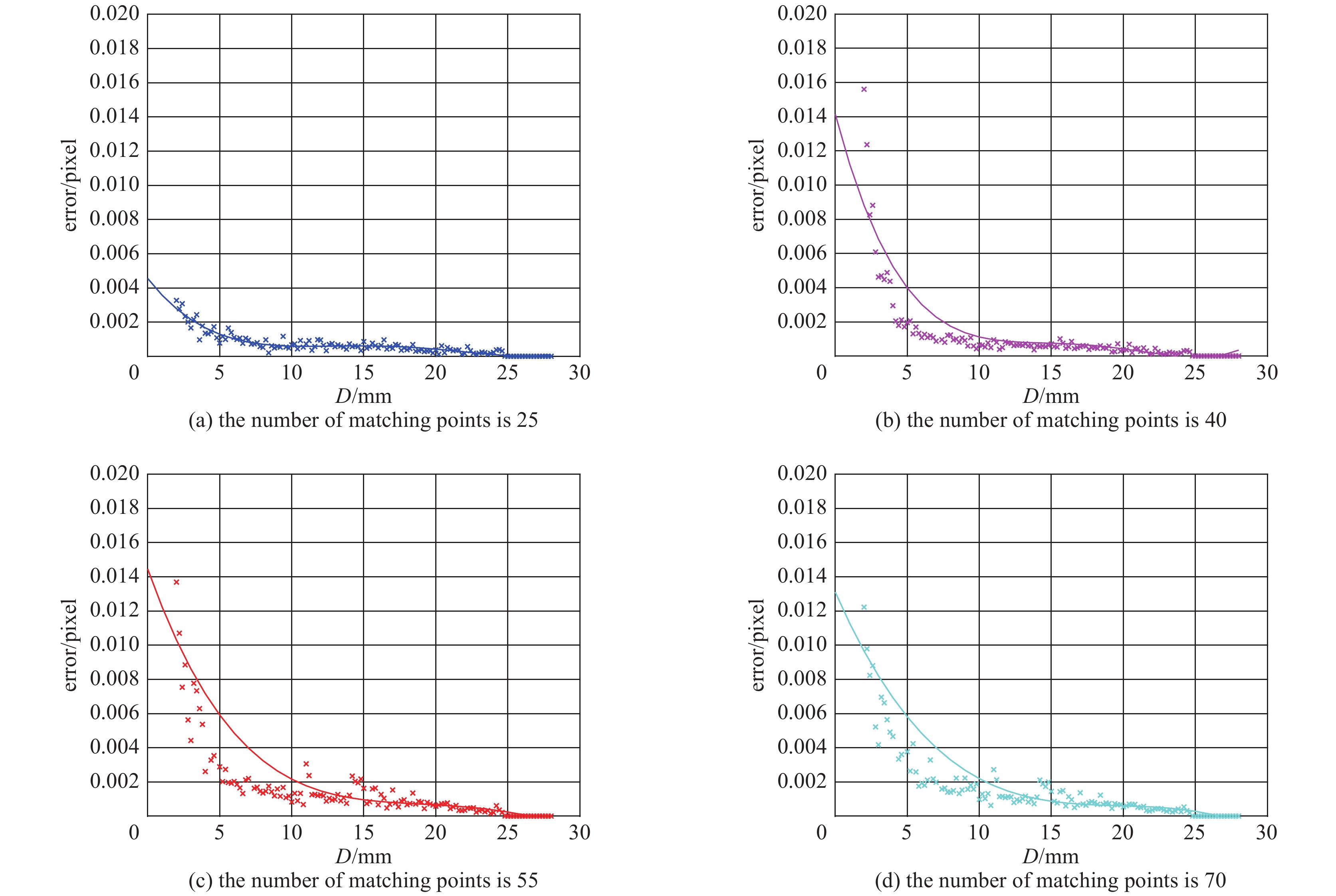
分别对这2张图像进行同样的处理，最后分别得到了这2组仿真实验在不同匹配点数目的条件下透镜孔径大小与系统误差之间的关系如图7、图8所示。

图  7  Cameraman：透镜孔径大小与系统误差之间的关系

Figure  7.  Relationship between lens aperture size and system error using “Cameraman” as input

下载: 全尺寸图片 幻灯片

图  8  Lena：透镜孔径大小与系统误差之间的关系

Figure  8.  Relationship between lens aperture size and system error using “Lena” as input

下载: 全尺寸图片 幻灯片

从图7和图8可以看出，当改变作为物的输入图像时，其仿真的结果与图5的仿真结果基本一致。

由这3组的仿真结果可以看出，对于输入的任何图像来说，在不同匹配点的条件下，随着透镜孔径的增大，系统误差持续减少，并且当透镜孔径增大到一定的数值时，系统误差趋近于0。因此，在设计双目视觉系统时，通过选取合适的透镜孔径大小，提高双目视觉系统的测量精度。

3.   实验验证及分析

3.1   实验设置

本文所需要的实验仪器主要包括数字工业相机、双胶合消色差透镜、电动光阑、电控平移台、二维组合平移台、分辨率测试靶、XY移动安装座、背光照明光源、激光器等。搭建好的实验平台如图9所示，实验仪器的相关参数如表1所示。

图  9  已搭建好的实验平台

Figure  9.  Established experimental platform

下载: 全尺寸图片 幻灯片

表  1  实验仪器的相关参数

Table  1.  Relevant parameters of the experimental instrument

laboratory apparatus	parameter values
digital industrial camera	resolution: 3840×2748; pixel size: 1.67 μm×1.67 μm
double cemented achromatic lens	diameter: ϕ25.4 mm; focal length: 30 mm
electric diaphragm	diameter range: ϕ2.5～28 mm
electronically controlled translation stage	moving direction: x; reading accuracy: 0.001 mm
two-dimensional combined translation stage	moving direction: x-y; reading accuracy: 0.001 mm
XY mobile mount	horizontal stroke: 50 mm; vertical stroke: 30 mm
resolution test target	size: 76.2 mm×25.4 mm
backlighting light source	power: 25 W; light source color: red
laser	wavelength: 532 nm; power: 50 mW

下载: 导出CSV 

| 显示表格

3.2   实验方案与方法

为了验证透镜孔径大小与系统误差之间的关系，需要固定视差值和物距。实验中通过电控平移台将分辨率测试靶分别向左向右平移，使其距离保持在1.16 mm，并结合光学倍率即可求出视差的真实值为80个像素值；分辨率测试靶离透镜的距离固定为300 mm。通过调节电动光阑的大小来限制参与成像的光束，其作用相当于改变了透镜的孔径大小，电动光阑的大小以间隔1 mm在5～26 mm范围内取值，当采集完所有图像后，将实验分为4组，分别在匹配点数目为25个、40个、55个、70个的条件下进行特征点提取和匹配并计算每组图像中匹配点的视差值，由于孔径尺寸会影响成像分辨率，导致SURF算法在进行特征点提取时产生偏差，计算出来的视差值为视差测试值，最后得出每组图像的视差均方根误差来表征系统误差，以此来分析透镜孔径大小与系统误差之间的关系。

具体的实验步骤为：

（1）搭建实验平台。

（2）调节电动光阑的大小，即改变透镜孔径的大小。

（3）将分辨率测试靶平移至视野中间的位置，然后将其向左移动0.58 mm，由工业相机采集左图。

（4）然后再将分辨率测试靶向右移动1.16 mm，同样由工业相机采集右图。

（5）重复步骤2，3，4，分别调节电动光阑的大小为5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26 mm，分别采集左右图像共22组，直至采集完所有图像后才进入下一步。

（6）对每一组图像分别提取特征点，提取的特征点数目分别设置为25，40，55，70个，并对所提取到的特征点进行匹配。

（7）计算每一组图像在不同匹配点数目下的视差值以及视差均方根误差来表征系统误差。

（8）分析透镜孔径大小与系统误差之间的关系。

其实验流程如图10所示。

图  10  实验流程图

Figure  10.  Flow chart of experiment

下载: 全尺寸图片 幻灯片

3.3   实验结果与分析

根据实验方案，结合计算机仿真结果进行实验，在不同匹配点数目的条件下一共得到了4组实验数据，为了更加直观地表示透镜孔径大小与系统误差之间的关系，同样采用了多项式拟合法将所得到的数据进行曲线拟合如图11所示。

图  11  透镜孔径大小与系统误差之间的关系

Figure  11.  Experimental relationship between lens aperture size and system error

下载: 全尺寸图片 幻灯片

与仿真实验结果基本一致，验证了仿真结果的准确性。由于在实验过程当中存在多种外在因素的干扰，因此不可避免地会引入各种误差，导致所获得的个别数据并不能够集中分布在拟合曲线的两侧，并且即使当透镜的孔径大小达到一定的数值时，其系统误差不能够像仿真结果一样近似于0，而是趋于一个较小的值。

4.   结　论

本文介绍了非相干双目成像、SURF算法和计算视差的原理，利用非相干成像理论仿真双目成像的过程，分析讨论了3组图像在不同匹配点下透镜孔径大小与系统误差之间的关系，通过实验验证了仿真结果的准确性，扩充了本领域的研究。最后得出结论：对于输入的任何图像来说，在不同匹配点数目的条件下，随着透镜孔径大小的增大，双目视觉测量系统误差减小，并且当透镜孔径大小取值为13 mm时，系统误差趋近于0。在其他的研究工作当中，许多工作都是致力于提高算法的提取和匹配的效果，而没有考虑到输入图像所携带信息的情况，如果采集的图像质量不好，即使算法的准确性和鲁棒性好，最终匹配效果也不够理想。而本文研究的是透镜孔径大小与系统误差之间的关系，这将为双目系统设计过程中孔径尺寸的选取提供理论和实验依据，进而使得立体匹配的效果达到最好。更进一步说，这将有利于双目视觉后续的一些工作的开展，如机器人导航、精密工业测量、物体识别、虚拟现实、场景重建等。