Self-consistent nonlinear numerical simulation of millimeter wave gyro-klystron amplifiers
-
摘要: 为了实现回旋速调管放大器的快速设计,基于经典的回旋管的稳态单模非线性理论方法,开展了回旋速调管放大器的束波作用效率的理论模拟研究。由于单模理论无法匹配回旋速调管放大器的输入腔、中间腔两端的突变边界条件,所以输入腔与中间腔都只能采用给定场法进行求解。回旋速调管的输出腔的功率输出端通常采用缓变结构,这种腔体可以采用单模自洽理论进行求解。对两腔毫米波回旋速调管放大器进行了理论模拟,并与商业粒子模拟软件的结果进行对比,验证了该数值理论模拟方法的有效性。Abstract: To realize quick design of the gyro-klystron amplifiers, a kind of numerical simulation method based on the single mode self-consistent nonlinear theory of gyrotrons was investigated. The single mode theory can’t be used to match the disrupt boundary conditions of the input and the middle cavities of the gyro-klystrons, thus the input and the middle cavities can only be processed through single mode theory based on given field distributions. As for the output cavities with smooth boundaries at the power output ends, the single mode nonlinear simulation could be self-consistent. A millimeter wave two cavity gyro-klystron amplifier with reported detailed parameters was simulated using the developed single mode theory. The effectiveness of the numerical simulation was verified by comparing the simulation results with those obtained in a commercial particle in cell (PIC) simulation tool.
-
由于效率潜力高、系统结构紧凑等优点,近年来超临界CO2布雷顿循环受到国内外的广泛关注[1-2]。针对其在太阳能、核能、余热回收、化石燃料等不同场景的应用,学者们也展开了相应的论证[3-4]。作为循环中体积最大、数量最多的部件,换热器的性能对循环效率影响显著,换热器的优化设计对系统的总体尺寸控制至关重要。
印刷电路板换热器(PCHE)是超临界CO2布雷顿循环中常用的换热器,可以满足高温高压的运行条件[5]。为方便设计计算,许多学者通过实验或仿真研究了CO2在PCHE中的流动换热特性,并拟合出相应的经验关系式。对于Z型通道的PCHE,Nikitin等[6]在2006年基于实验数据和数值计算结果,分别给出了热通道2800<Re<5800和冷通道6200<Re<12100在跨临界范围内的换热关系式。2009至2011年,Kim等[7-8]测试了亚临界状态下He-He和He-H2O工质对在PCHE中的流动换热特性,分析总结出Re<2500范围内的经验关系式。Kim等[9]在2016年通过数值方法,计算了跨临界状态下不同夹角的Z型通道内CO2的流动换热特性,并总结出了2000<Re<58000范围内的经验关系式。同年,Chen等[10]利用亚临界状态He测试并总结出特定结构PCHE的换热经验关系式。由于CO2物性不同于常规流体,且在临界点附近变化剧烈,现有的经验关系式所适用的范围有限,仅可保证特定几何结构和特定工况下的准确性。设计过程中,采用不同的经验关系式计算所得的结果往往存在较大差异。且根据经验关系式作设计计算所得的为换热面积,需要进一步细化和优化结构参数。然而,现有研究在比较不同几何结构对换热性能的影响时,重在讨论通道尺寸、通道形式等,大多忽略了几何结构的变化导致换热面积不同这一要素[11-12]。而对于换热器而言,换热面积往往是决定换热性能最重要的因素。
因此,本文重点分析了当换热面积固定时,回热器的不同几何结构对流动换热特性的影响,明确影响换热性能的关键因素,为回热器的优化设计提供理论依据。
1. 模型建立
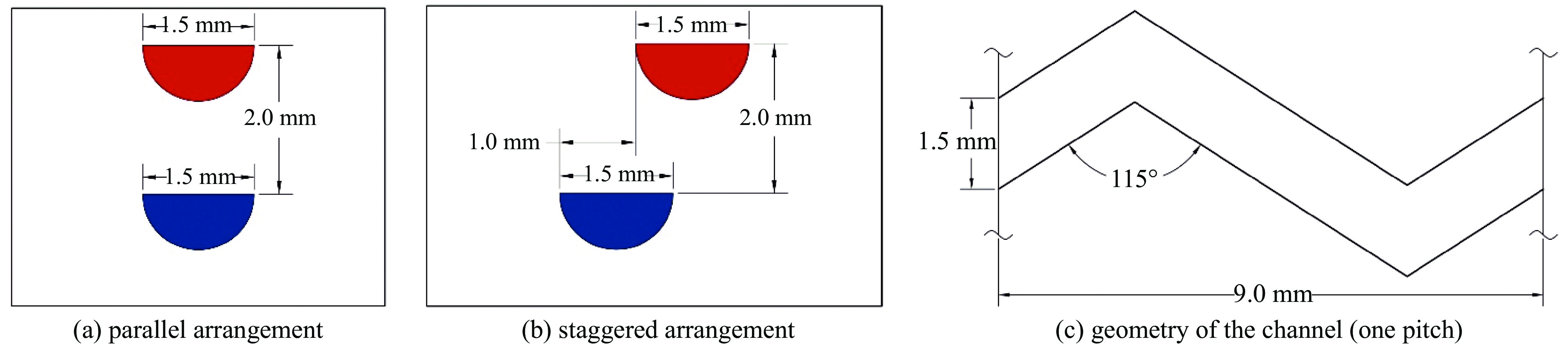
表1所示为中国科学院工程热物理研究所某回热器测试件的结构参数,该回热器采用Z字型通道,通道横截面为半圆形,直径1.5 mm,在板厚为2 mm的SS 316L钢板上进行化学蚀刻形成。回热器冷热通道结构相同,冷热板片交替堆放[13]。
表 1 回热器测试件结构参数Table 1. Geometry information of the test recuperatorchannel diameter/mm channel included angle/(°) pitch size/mm plate No. channel No. at each plate pitch No. hot side 1.5 115 9 30 27 60 cold side 1.5 115 9 31 27 1.1 计算单元模型
由于通道数量较多,且排列方式具有明显的周期性,为减少计算量,对回热器的结构进行简化,计算由一个热流道和一个冷流道构成的单元,并在四周设置周期性边界条件。回热器单元的结构如图1所示。
图1展示了冷热通道的两种不同排布方式,即顺排和叉排,考虑到高温高压下不锈钢板的力学性能,一般采用叉排方式。但由于文献[13]中未提及这一点,在模型验证时对这两种排布方式的换热特性都进行了计算。沿长度方向冷热通道的结构如图1(c)所示,为便于与实验结果进行比较,计算过程中不减少节距数,即回热器单元总长为540 mm。
1.2 网格划分
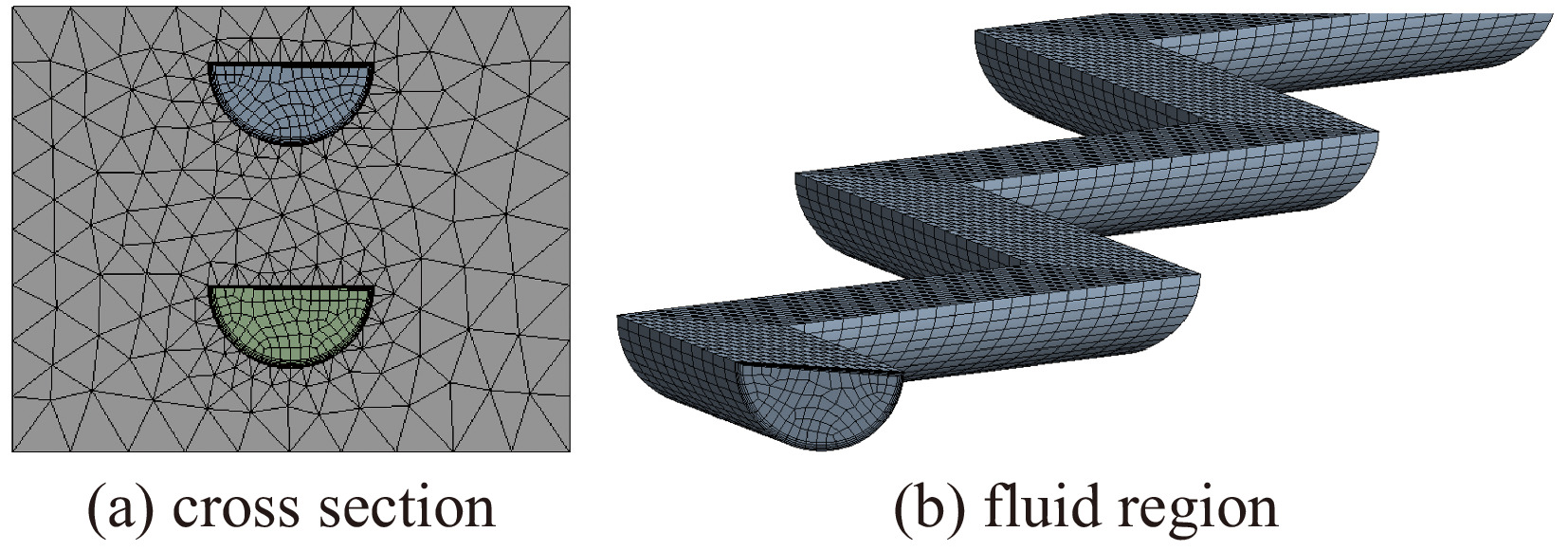
采用CATIA建立回热器单元的固体域模型,将其导入ANSYS Workbench中的Geometry模块,再利用“填充”指令构建回热器单元的流体域模型。
为保证流体域的网格质量,采用MultiZone方法进行流体域网格的划分,固体域采用非结构化网格。固体与流体的交界面采用控制第一层网格厚度的方式划分边界层网格,在进行网格无关性验证的过程中分别将第一层网格厚度设定为0.01 mm和0.015 mm,边界层层数设置了8层和5层两种不同规格,对应的生长率设定为1.12和1.2。以边界层第一层厚度为0.01 mm为例,回热器单元横截面以及流体域的网格如图2所示。
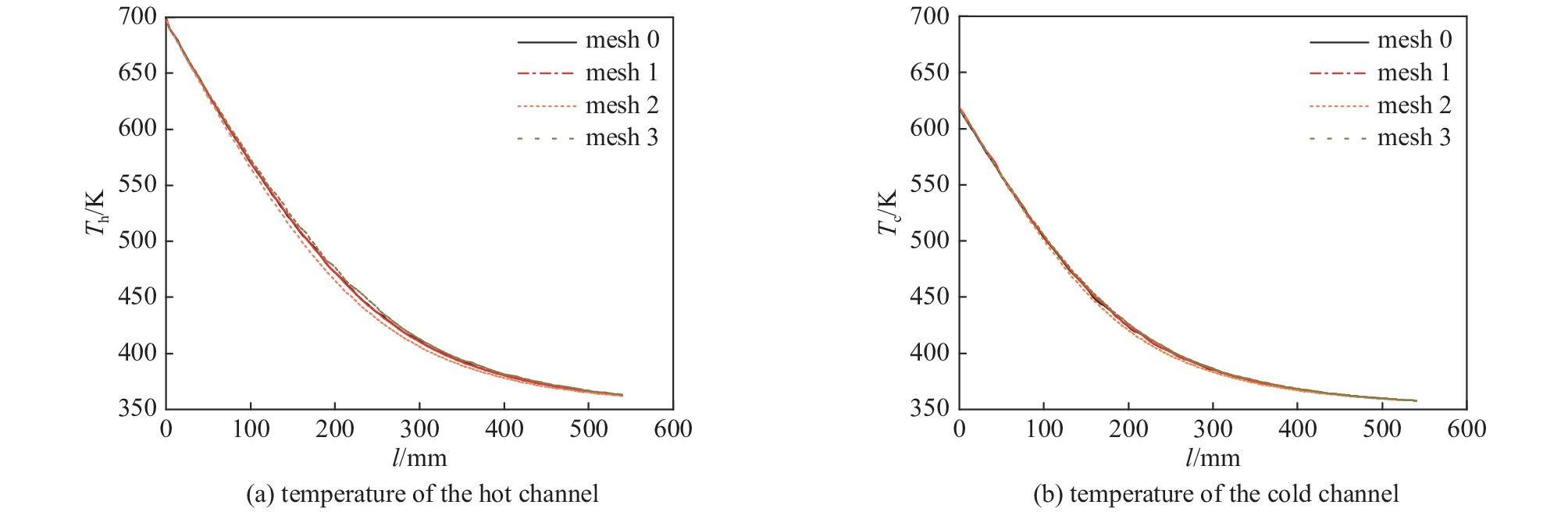
综合考虑计算机资源和计算时间等因素,比较了网格数量为2 320 018,5 522 582,8 762 918和10 653 951时回热器单元的换热特性。对应的热流体区域网格数量分别为420 480,741 840,1 630 223和1 951 200;冷流体区域的网格数量分别为408 960,741 840,1 636 705和1 832 400;固体域网格数量分别为1 490 578,4 038 902,5 495 990和6 870 351,所得计算结果如图3所示,冷热通道的温度与压力参数设置参照表2中case1进行。可以看出,随着网格数量的变化,冷热通道中CO2的温度变化曲线非常接近,以网格数量为5 522 582的算例作为参考,计算所得换热量偏差不超过±1%。为减少计算量,在进行后期其他结构的网格划分时,采用与网格数量为5 522 582算例类似的设置。
表 2 换热性能计算结果与实验结果对比Table 2. Comparison of the heat transfer performance between simulation and testscondition Th,i/K Th,o/K ph/MPa Tc,i/K Tc,o/K pc/MPa η/% case1 test 699.45 369.15 8.4 357.75 610.85 19.3 95.2 parallel 699.45 362.78 8.4 357.75 617.48 19.3 97.2 stagered 699.45 362.75 8.4 357.75 617.68 19.3 97.3 case2 test 705.15 363.25 7.6 355.45 601.85 20.6 94.2 simulation 705.15 360.43 7.6 355.45 619.95 20.6 98.2 1.3 边界条件
本研究采用ANSYS Fluent进行数值模拟,前期研究中使用较多的湍流模型为SST k-ω模型和标准k-ε模型[14-15]。由于SST k-ω模型是混合模型,在近壁面保留了原始的k-ω模型,在远离壁面区域应用了k-ε模型,因此超临界CO2在微通道中的流动换热计算广泛采用SST k-ω模型。为了得到更精确的计算结果,本文采用两种模型进行了计算,采用标准k-ε模型和SST k-ω模型计算所得的换热量相对实验结果的误差分别为3%和1%左右,因此后续其他结构的计算均采用SST k-ω模型。对于本文涉及的工况,具体以参考文献[13]中的结构为例。
固体域SS 316L的物性参数直接从Fluent中的GRANTA MDS物性库中选取,冷热流体域超临界CO2的物性参数从NIST-REFPROP数据库获取,拟合成温度的函数导入Fluent中。
根据参考文献[13]中所给的进出口条件,将冷热流体入口设置为质量流量入口,冷热流体出口均设置为压力出口,具体参数设置如表2中case1所示。
由于所选取的计算单元只是回热器中冷热流体通道阵列的一部分,如图2所示,回热器单元的四周设置为周期性边界条件。长度方向没有做简化处理,接近真实的回热器结构,为简化计算,将流体进出口侧的固体壁面设置为绝热壁面。
2. 模型验证
对于超临界CO2布雷顿循环中的回热器而言,换热效率是衡量其换热性能的一个重要指标。由于换热过程中超临界CO2的比热容变化较大,常规换热器的换热效率定义式不再适用,采用基于焓值的计算方法,综合夹点问题的考虑,回热器的换热效率η定义如下[16]
η = QrealQideal (1) Qideal=min(Q1,Q2,Q3) (2) Q1=mh{H(Th,i,ph)−H(Tc,i,ph)} (3) Q2=mc{H(Th,i,pc)−H(Tc,i,pc)} (4) Q3=mh{H(Th,i,ph)−H(Tm,ph)}+mc{H(Tm,pc)−H(Tc,i,pc)} (5) 式中:η表示换热效率;Q表示换热量(kW,下标real表示实际换热量,ideal表示理论最大换热量);m表示质量流量(kg∙s−1),p表示压力(Pa),下标h与c分别代表热流道和冷流道;T表示温度(K),i表示入口;H表示焓值(kJ∙kg−1);Tm代表夹点温度,可通过计算冷热流体在夹点处的温度平均值而得(K)[17]。
为保证超临界CO2布雷顿循环的效率,需精确控制压缩机入口的工质参数,换热器便是循环中达到此目的的重要环节,因此回热器的进出口参数也是重要指标。表2中对比了两种不同工况下计算和实验所得的回热器进出口温差及换热效率,因文献[13]中未明确通道阵列的排布方式,故将顺排和叉排两种排布方式的计算结果均与case1的实验结果进行了对比。
从表2可以看到,计算所得的冷热通道进出口温差与实验结果接近。case1顺排和叉排两种排布方式与实验结果的偏差不超过±3%,case2热通道偏差约1%,冷通道偏差约7%。从表1的板片数可以看到,靠近壳体为冷流道,存在更多的热量损失,也造成了冷流道计算结果与实验结果更大的偏差。两个算例换热效率与实验结果同样非常接近,case1顺排和叉排的计算值与实验测试值的偏差为2%左右,case2的计算值与测试值偏差为4%左右。因此,可以应用该模型进行分析计算。此外,为了减小金属材料的热应力,PCHE的通道排布方式通常选择叉排,但从计算结果可以看出,两种排布方式的换热性能差异非常小。为了减少网格数量,节省计算时间,后续其他结构的计算按照顺排的方式进行。
3. 结果与分析
减小Z型通道夹角和增加通道长度均可达到强化换热的目的,此两种方式也都会增加换热面积。减小Z型通道夹角会增加局部阻力,从而导致压降增大。增加通道长度相当于增加沿程阻力,同样也会导致压降增大,且增加通道长度会增大回热器的尺寸和重量,此外,由于PCHE价格高昂,还会导致成本的上升。因此,回热器的优化设计需要综合对比分析以上各要素。
为了明确回热器的优化设计方法,以下对比了当换热面积不变,Z型通道夹角分别为105°,110°,115°,120°和125°时的流动换热性能。
3.1 换热性能分析
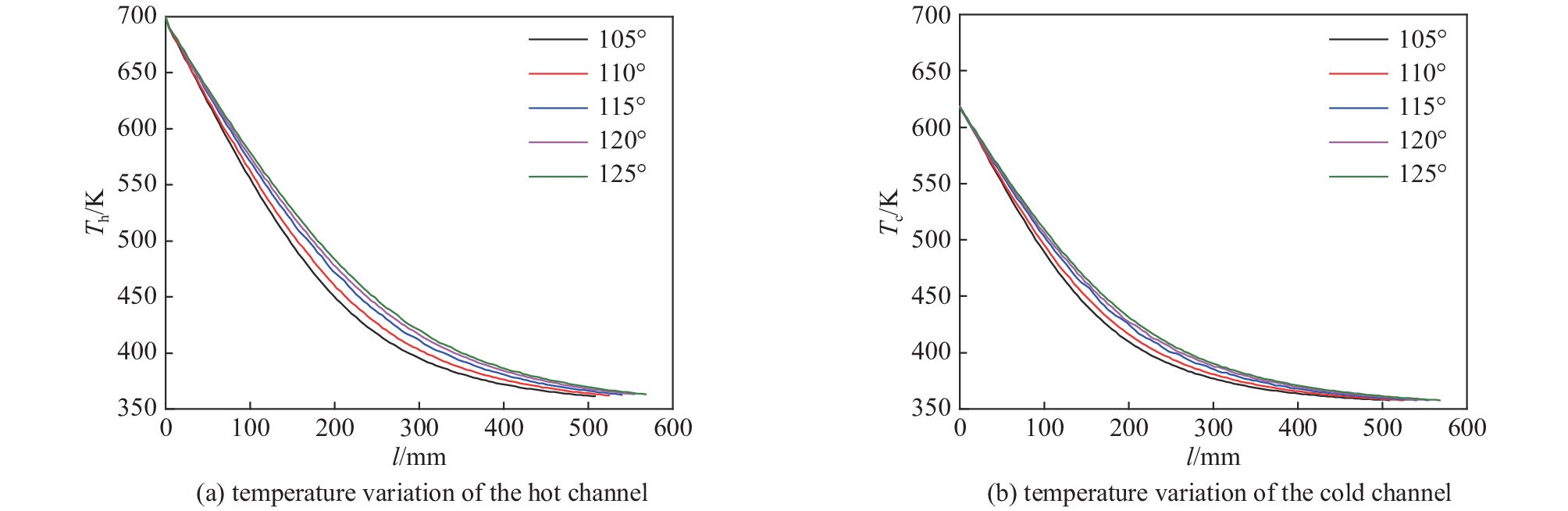
相比实验测试,CFD计算的优势在于可以明确回热器内部的流场与温度场。为了直观地比较不同夹角下的换热性能,图4中首先对比了通道截面的平均温度沿长度方向的变化。
从图4中可以看到,随着通道夹角的增加,冷热通道流体的温度变化速率均逐渐减缓,当通道夹角大于115°后夹角的进一步增大带来的流体温度变化幅度减小。由此说明减小通道夹角可有效强化换热,但并非随着夹角的减小线性提高,Z型通道夹角的选择存在最佳范围。此外,回热器热端冷热通道内CO2的温度变化速率均明显高于冷端,这主要是由于热端的换热温差更大。其中,通道夹角为105°时热端冷热通道内CO2的温度变化最快,在冷端端头附近100 mm冷热通道内CO2的温度变化不足热端端头附近100 mm温度变化的1/10,据此可以初步判定回热器冷端的换热量低于热端。同时,这也意味着不锈钢板两头存在较大的温差,从而导致力学性能的差异。
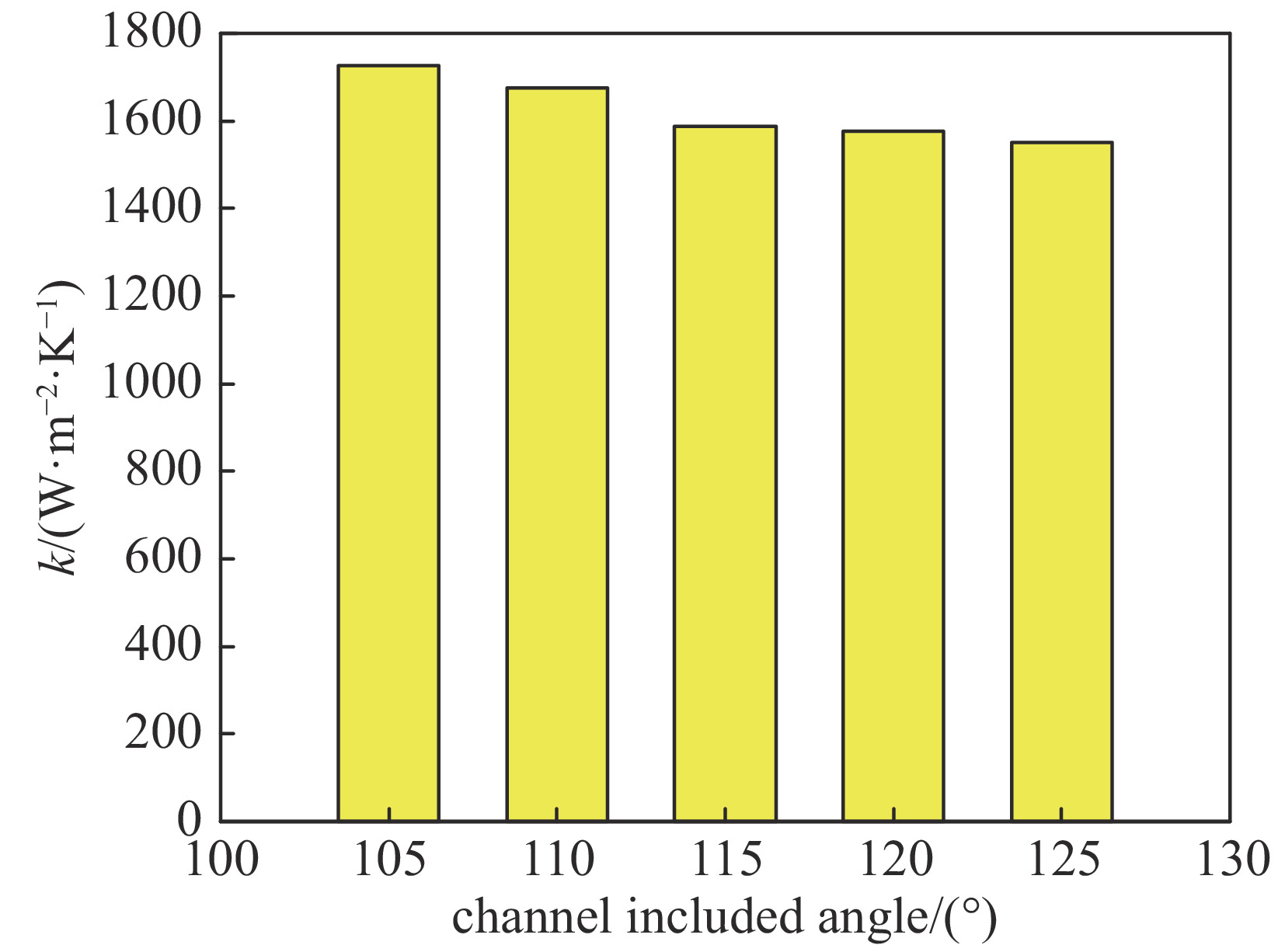
从冷热通道CO2的进出口温度来看,5种结构的差异并不明显,说明整体换热性能比较接近。换热系数是衡量换热器结构设计优劣的重要指标,是与换热面积和换热温差无关的量。为了进一步说明通道夹角的变化所带来的换热性能变化,图5中对比了五种结构回热器的总体换热系数。
随着通道夹角的增加,总换热量其实并没有太大的变化,图4中冷热通道CO2的进出口温度相近也可以佐证这一点。但整体换热系数却存在比较明显的差异,这主要是由于冷热通道内CO2的平均换热温差造成。通道夹角为105°时,冷热通道CO2在回热器冷端较长的距离内保持着小温差,从而导致平均温差较小,因此其整体换热系数最高。从图4中可以看到,不同通道夹角的回热器之间热通道内CO2温度差异较冷通道大,因此冷热通道CO2的换热温差会随着通道夹角的增大而增大,从而使得整体换热系数呈下降趋势。与图4中CO2温度的变化趋势类似,当通道夹角从110°增加至115°时换热系数的变化幅度最大,通道夹角为115°~125°时冷热通道CO2的温度接近,其换热系数也无明显差别。
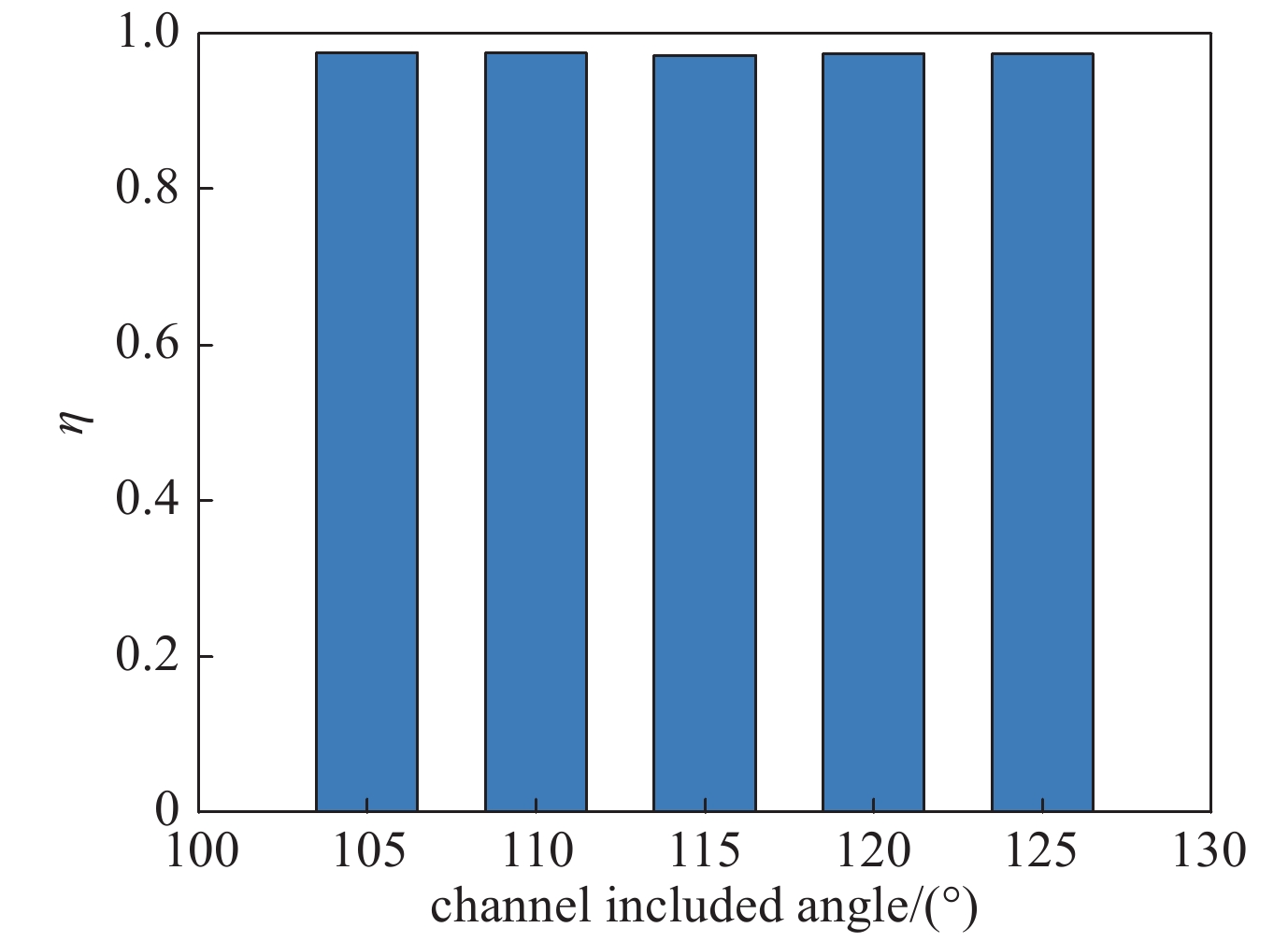
由于超临界CO2比热容的大幅变化,虽然回热器冷端端头冷热通道CO2的换热温差已小于6 K,热端端头冷热通道CO2却仍然存在较大的温差。为了说明热端端头的温差并不意味着大量的热能未被成功回收,图6中对比了五种结构回热器的换热效率。可以看到,虽然不同的通道夹角造成了回热器换热系数的差异,该工况下五种结构的回热器回热效率却无明显差距,均在97%以上。由此说明该换热面积已使得该工况下的冷热通道CO2接近换热极限,实现了热能的有效回收。结合图4可以推断,若同时减少换热面积,则不同的结构会有不同的换热效率。
3.2 流动性能分析
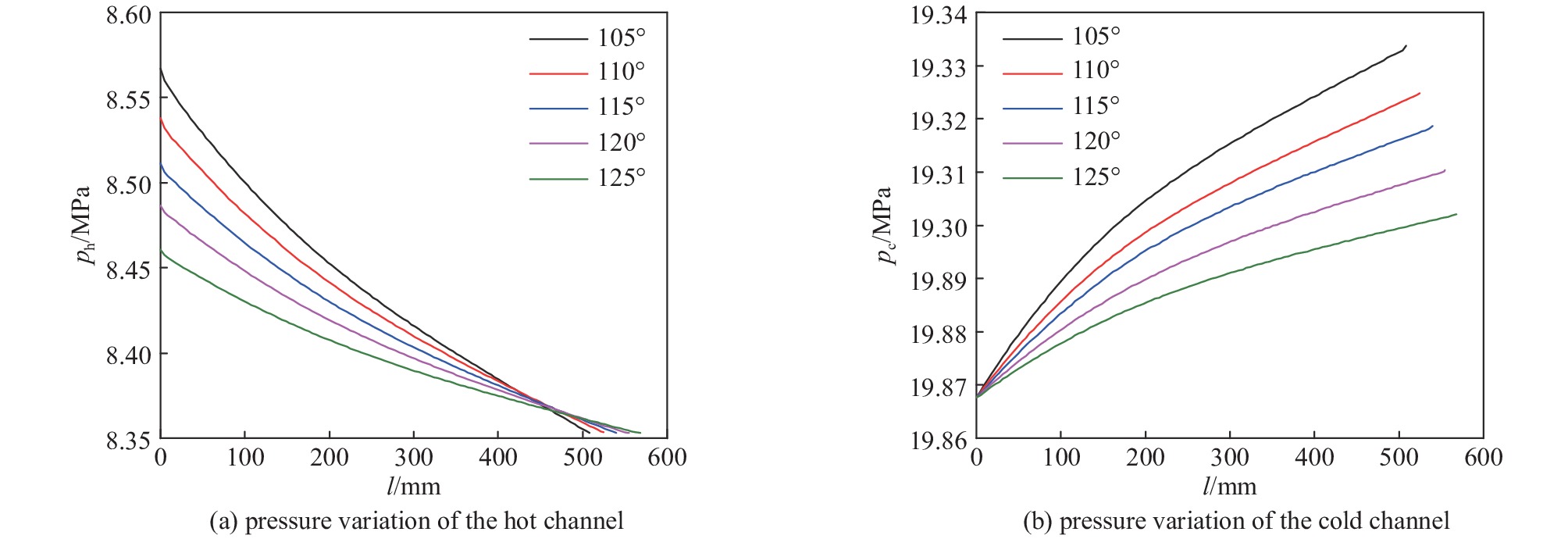
由于采用微通道,整个布雷顿循环的阻力损失主要来自换热器,因此,压降也是回热器设计需要重点考虑的因素。图7中分别对比了冷热通道中的压力变化。
从图7(a)中可以看到,热通道内CO2的压力降低速率逐渐减缓,这主要是由于密度和粘性的变化。随着温度的降低,密度逐渐变大,从而流速降低,因此流动阻力损失减少。此外,该温度区间内粘性系数随着温度的降低而降低,同样也会使得阻力损失减少。图7(b)中也可以观察到类似的现象。相对温度而言,冷热通道CO2在长度方向的压力变化更接近线性,因为当温度从400 K降至350 K,CO2的比热容急剧升高,再加上换热温差的减小,从而导致图4中低于400 K段的温度变化速率缓慢。
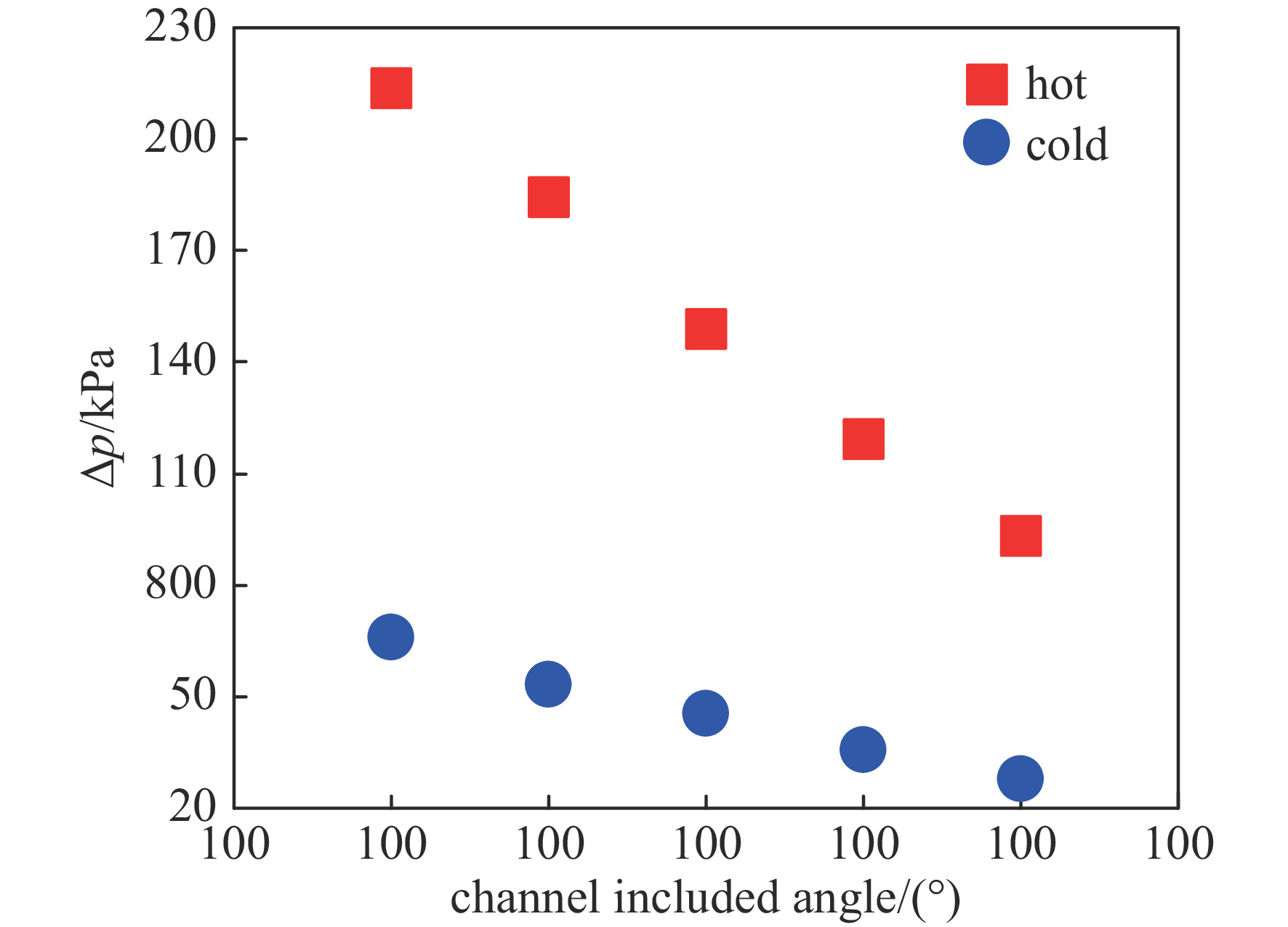
为了明确减小Z型通道夹角对流动阻力的影响,图8中对比了5种设计方案的冷热通道进出口压降。可以看到,冷热通道内的压降随着通道夹角的增大的确逐渐减小,但变化速率不同。由于热通道内压力相对较低,CO2的密度也较冷通道内低,因此热通道内CO2的流速更快,流动阻力损失更大,对通道夹角的变化也更敏感。冷通道内的压降变化线性度相较热通道低,以实验测试件即115°夹角为参考基准,105°和110°夹角减少回热器长度所需付出的压降代价分别为640 Pa/mm和509 Pa/mm,120°和125°夹角增加回热器长度所带来的压降收益分别为669 Pa/mm和623 Pa/mm。结合换热性能考虑,将通道夹角减小至110°可明显提高换热系数。由于PCHE造价高昂,减小通道夹角还可同时降低回热器成本,但将通道夹角进一步减小至105°则会导致压降的大幅上升。将通道夹角增大至120°可明显降低压降,且对换热性能不造成显著影响,但继续增大通道夹角来降低压降则会导致成本的快速上升。因此,Z型通道的夹角宜在110°~120°之间选取,根据应用场景对压降和成本的控制要求选择合适的结构。
4. 结 论
本研究采用CFD计算,分析对比了相同换热面积、不同通道结构的回热器的换热性能,得到如下结论:
(1)通道内CO2的温度沿着流动方向呈现出非常明显的非线性变化,回热器热端的温度变化速率明显高于冷端。
(2)由于换热面积相同,不同通道结构的回热器换热效率并无明显差异,但换热系数不同。当通道夹角从110°增加至115°时换热系数出现明显下降,超过115°后几乎没有变化。
(3)综合换热性能、压降与成本三方面考虑,Z型通道回热器的通道夹角最佳范围为110°~120°。对于换热量大的场合,为提高换热性能和降低成本可选择110°夹角,对于需严格控制压降的场合,可选择120°夹角。
本研究可用于相近结构和尺寸的回热器设计参考,对于通道尺寸相差较大的回热器或者冷却器的参考性有待进一步验证。
-
表 1 Ka波段两腔二次谐波回旋速调管放大器参数
Table 1. Parameters of a Ka band two cavity second harmonic gyro-klystron amplifier
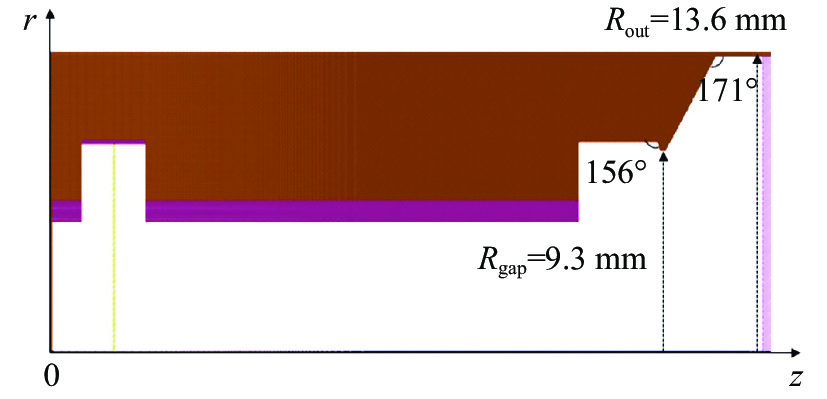
stage radius/mm length/mm Q frequency/GHz input 9.77 20.6 300 35.0 output 9.66 25.3 610 34.96 drift 7.0 122 -
[1] Danly B G, Blank M, Calame J P, et al. Development and testing of a high-average power, 94-GHz gyroklystron[J]. IEEE Transactions on Plasma Science, 2000, 28(3): 713-726. doi: 10.1109/27.887710 [2] 罗勇. 回旋速调放大器高频系统及注-波互作用研究[D]. 成都: 电子科技大学, 2003Luo Yong. High frequency system and beam-wave interaction study of gyro-klystron amplifiers[D]. Chengdu: University of Electronic Science and Technology of China, 2003 [3] 罗勇, 李宏福. 回旋速调管放大器注-波互作用分析[J]. 强激光与粒子束, 2005, 17(5):724-728. (Luo Yong, Li Hongfu. Study on the interaction between electron beam and waves in gyroklystron amplifiers[J]. High Power Laser and Particle Beams, 2005, 17(5): 724-728 [4] Chu K R. The electron cyclotron maser[J]. Reviews of Modern Physics, 2004, 76(2): 489-540. doi: 10.1103/RevModPhys.76.489 [5] Levush B, Blank M, Calame J, et al. Modeling and design of millimeter wave gyroklystrons[J]. Physics of Plasmas, 1999, 6(5): 2233-2240. doi: 10.1063/1.873476 [6] Latham P E, Lawson W, Irwin V. The design of a 100 mw, Ku band second harmonic gyroklystron experiment[J]. IEEE Transactions on Plasma Science, 1994, 22(5): 804-817. doi: 10.1109/27.338296 [7] Vlasov A N, Antonsen T M, Jr Chernin D P, et al. Simulation of microwave devices with external cavities using MAGY[J]. IEEE Transactions on Plasma Science, 2002, 30(3): 1277-1291. [8] 马俊建, 朱小芳, 金晓林, 等. 回旋速调管放大器时域非线性理论与模拟[J]. 物理学报, 2012, 61:208402. (Ma Junjian, Zhu Xiaofang, Jin Xiaolin, et al. A time-dependent nonlinear theory and simulation for gyroklystron amplifier[J]. Acta Physica Sinica, 2012, 61: 208402 doi: 10.7498/aps.61.208402 [9] Fliflet A W, Read M E, Chu K R, et al. A self-consistent field theory for gyrotron oscillators: application to a low Q gyromonotron[J]. International Journal of Electronics, 1982, 53(6): 505-521. doi: 10.1080/00207218208901545 [10] 刘迎辉, 李宏福, 雷朝军, 等. 输入腔高频场的矩阵分析[J]. 强激光与粒子束, 2007, 19(6):931-933. (Liu Yinghui, Li Hongfu, Lei Chaojun, et al. Analysis of RF field in an input cavity by parameter matrix[J]. High Power Laser and Particle Beams, 2007, 19(6): 931-933 [11] 耿志辉, 刘濮鲲. 回旋速调管放大器输出腔的特性研究[J]. 强激光与粒子束, 2004, 16(11):1445-1448. (Geng Zhihui, Liu Pukun. Characteristic study of output cavity in gyroklystron amplifier[J]. High Power Laser and Particle Beams, 2004, 16(11): 1445-1448 [12] Geng Zhihui, Liu Pukun. Design of a Ka-band second harmonic gyroklystron amplifier by using a self-consistent nonlinear simulation[J]. IEEE Transactions on Plasma Science, 2006, 34(3): 534-540. doi: 10.1109/TPS.2006.875761 [13] Zhou Jun, Liu Dagang, Liao Chen, et al. CHIPIC: an efficient code for electromagnetic PIC modeling and simulation[J]. IEEE Transactions on Plasma Science, 2009, 37(10): 2002-2011. doi: 10.1109/TPS.2009.2026477 [14] 耿志辉. 毫米波回旋速调管放大器的自洽非线性理论与模拟[D]. 北京: 中国科学院研究生院(电子学研究所), 2005Geng Zhihui. Self-consistent nonlinear theory and simulation of millimeter wave gyro-klystron amplifier[D]. Beijing: Institute of Electronic, Chinese Academy of Sciences, 2005 [15] 孙迪敏. W波段三次谐波回旋管理论与实验研究[D]. 北京: 清华大学, 2014Sun Dimin. Theoretical and experimental study of W-band third harmonic gyrotrons[D]. Beijing: Tsinghua University, 2014 -





 下载:
下载:



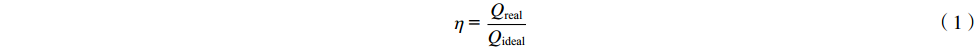
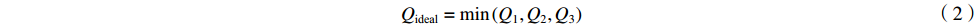
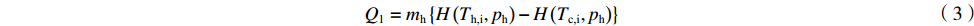
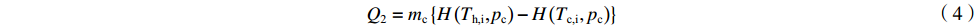
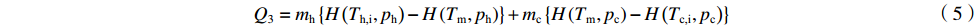





 下载:
下载: