Study on nonstationary oscillation in continuous frequency tunable terahertz gyrotron
-
摘要: 太赫兹回旋管可实现高功率输出,并具有一定的频率调谐范围,是核磁共振波谱系统理想的高功率太赫兹辐射源。设计了263 GHz,TE5,2基波连续调谐回旋管,通过磁场调节实现频率调谐范围为1.39 GHz,利用时域多模多频自洽非线性理论对设计的连续调谐回旋管非稳定振荡状态进行了研究。结果表明,在低次纵向谐波模式工作磁场范围内,当工作电流大于起振电流时,连续调谐回旋管先进入稳定状态,高次纵向谐波模式被抑制,工作模式TE5,2的输出功率随时间不变;当电流增大,纵向谐波模式间的竞争引起回旋管由稳定状态进入到非稳定振荡状态,工作模式TE5,2的输出功率随时间呈振荡变化且互作用效率大大降低;随着电流的进一步增大,回旋管又回到与低电流不同的稳定状态,互作用效率进一步降低。同时发现非稳定振荡状态的起始电流随着磁场增加而增大。本研究对需工作于稳定状态的面向DNP-NMR应用的连续调谐太赫兹回旋管的研制具有一定指导意义。Abstract: Terahertz gyrotron can achieve high output power and has a certain frequency tuning range, thus it is an ideal high power terahertz radiation source for NMR spectroscopy system. A 263 GHz, TE5,2 fundamental harmonic frequency continuously tunable gyrotron is designed, the corresponding frequency tuning range can reach 1.4 GHz through adjusting the magnetic field. The unstable oscillation state of the designed gyrotron is studied by using the time domain multi-mode multi frequency self-consistent nonlinear theory. The results show that in the magnetic field range of low order axial mode, when the operating current is greater than the starting current, the continuously tuned gyrotron enters the stable state, where the high order axial mode is suppressed, and the output power of TE5,2 remains unchanged with time. When the current increases, the competition between axial modes causes the gyrotron to enter the unstable oscillation state from the stable state, the output power of TE5,2 oscillates with time and the interaction efficiency decreases greatly. With the further increase of current, the gyrotron returns to another stable state different from that of low current. It is also found that the initial current increases with the increase of magnetic field. The research of this paper has a certain guiding significance for the development of continuously tuned THz gyrotron for DNP-NMR applications.
-
Key words:
- terahertz /
- gyrotron /
- nonstationary oscillation /
- continuously frequency tuning
-
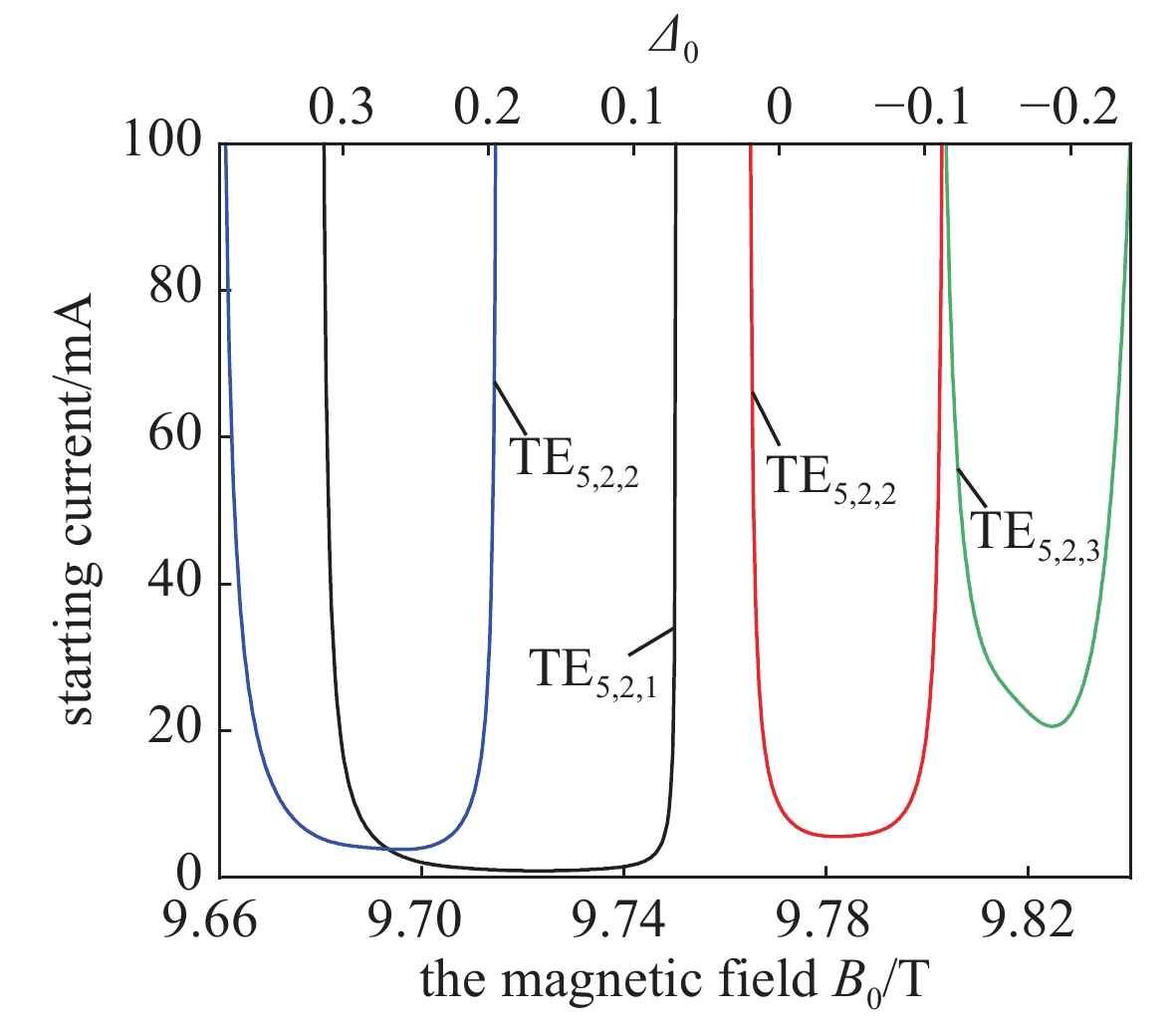
图 2 不同纵向谐波模式起振电流(
$ {\rm{\sigma }}=2.9\times {10}^{7} $ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ )Figure 2. Starting currents of different order axial modes (wall conductivity
$ {\rm{\sigma }}=2.9\times {10}^{7} $ S/m, beam voltage$ {U}_{0}=20 $ kV, beam guiding center$ {R}_{\rm{g}}=1.4 $ mm, pitch angle$ {\rm{\alpha }}=1.75 $ )图 3 稳定工作状态(
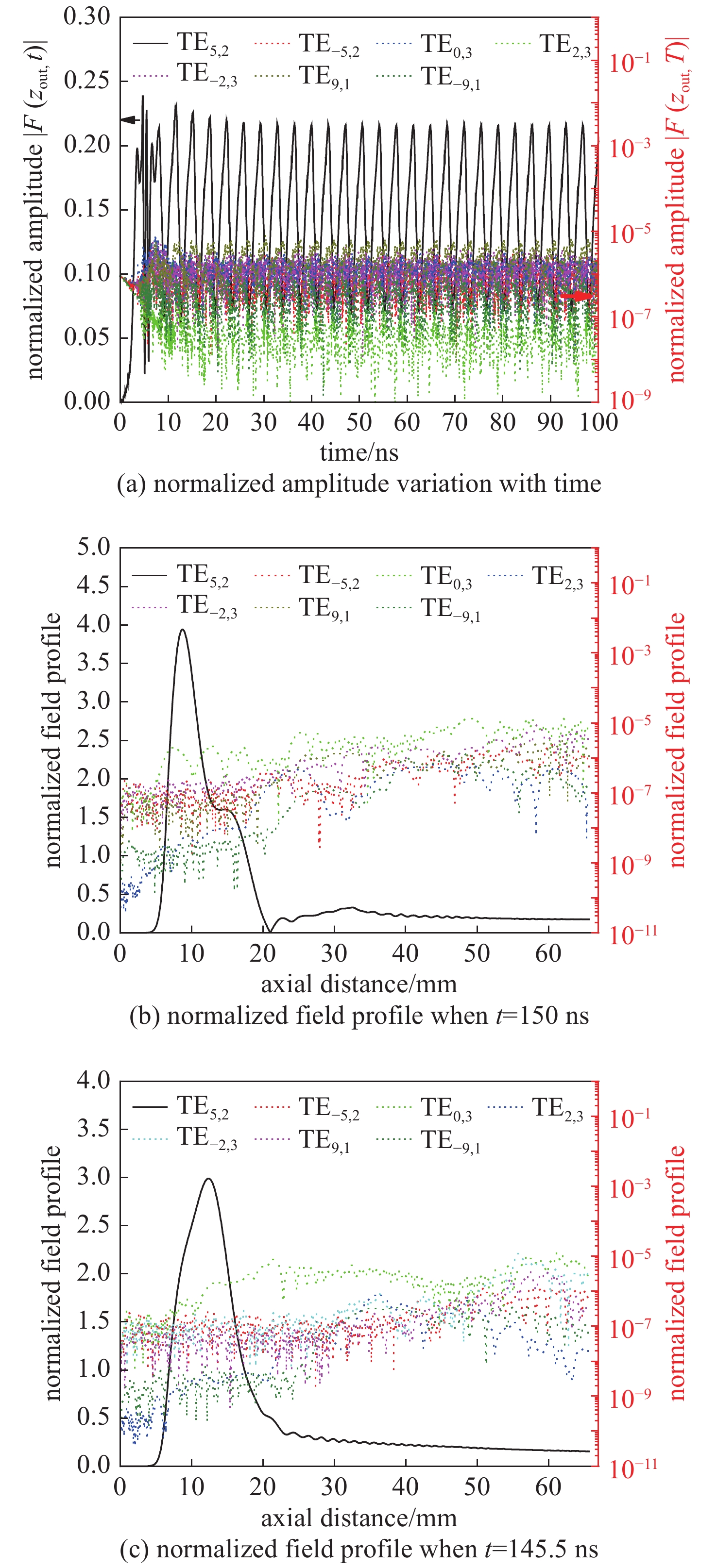
$ {\rm{\sigma }}={\infty } $ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.65 $ T,$ {I}_{0}=25 $ mA)Figure 3. Stationary oscillation when
$ {\rm{\sigma }}={\infty } $ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.65 $ T,$ {I}_{0}=25 $ mA图 4 稳定工作状态(
$ {\rm{\sigma }}={\infty } $ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.65 $ T,$ {I}_{0}=25 $ mA)Figure 4. Stationary oscillation when
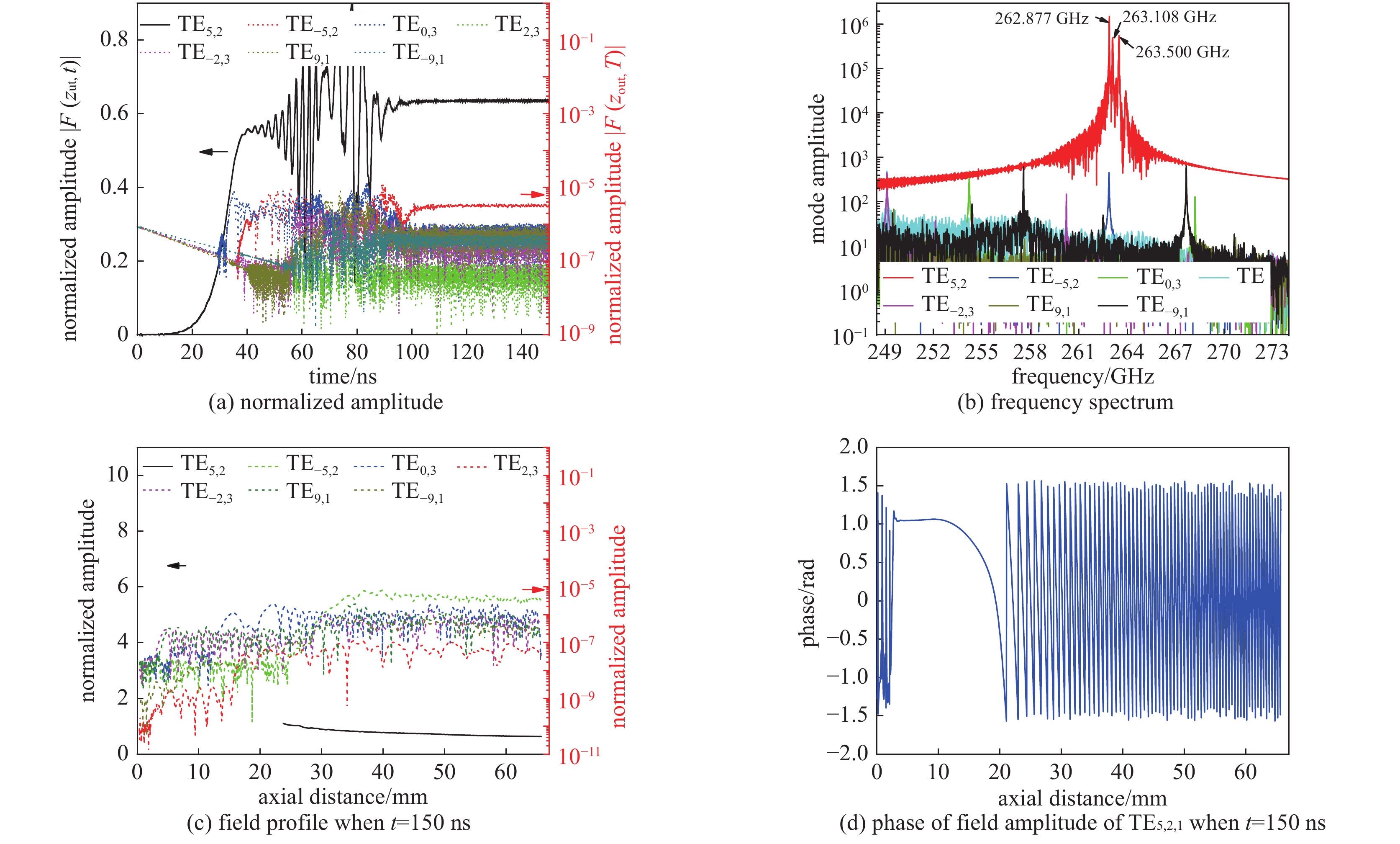
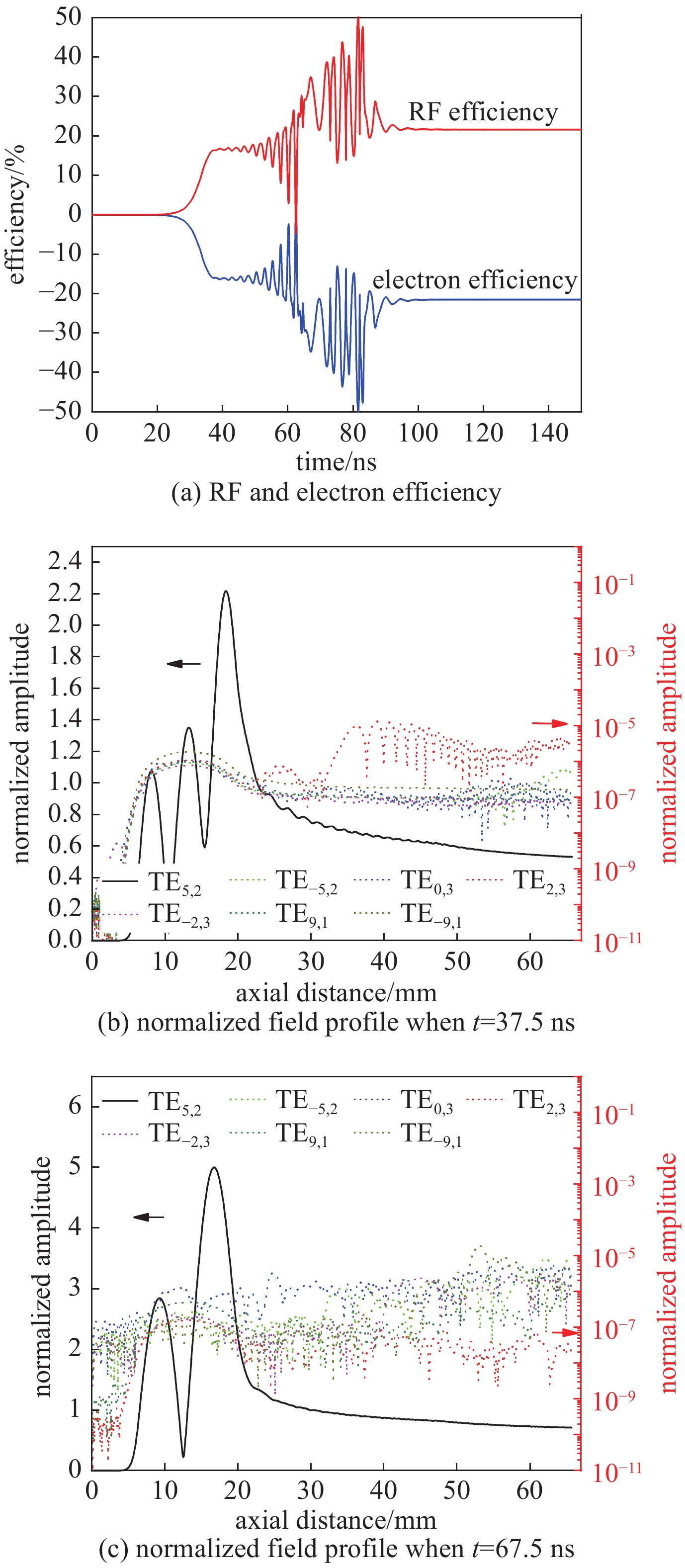
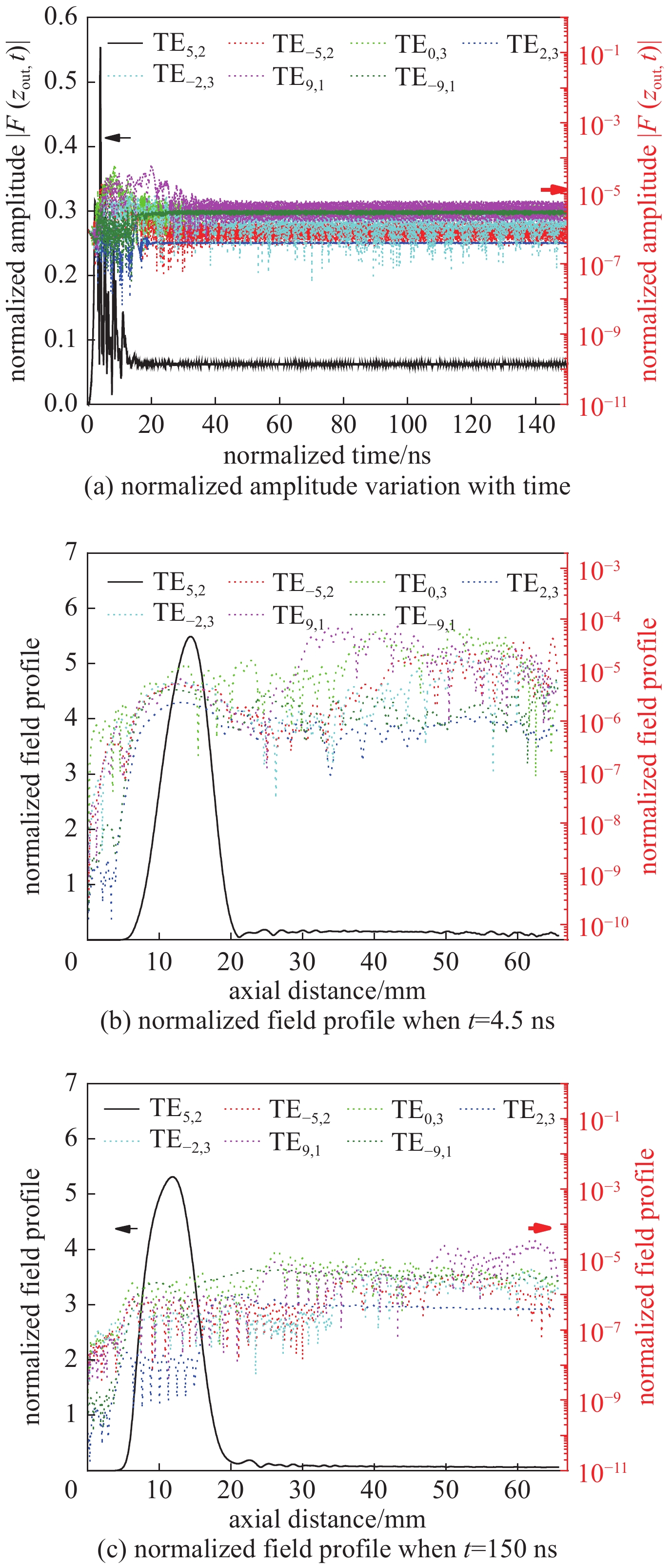
$ {\rm{\sigma }}={\infty } $ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.65 $ T,$ {I}_{0}=25 $ mA图 5 模拟得到的连续调谐回旋管非稳定工作状态,其中
${\rm{\sigma }}=2.9\times $ $ {10}^{7}$ ,$ {U}_{0}= 20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=25 $ mAFigure 5. Nonstationary oscillation when
$ {\rm{\sigma }}=2.9\times {10}^{7} $ S/m,$ {U}_{0}= $ $ 20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=25 $ mA图 6 连续调谐回旋管非稳定工作状态(
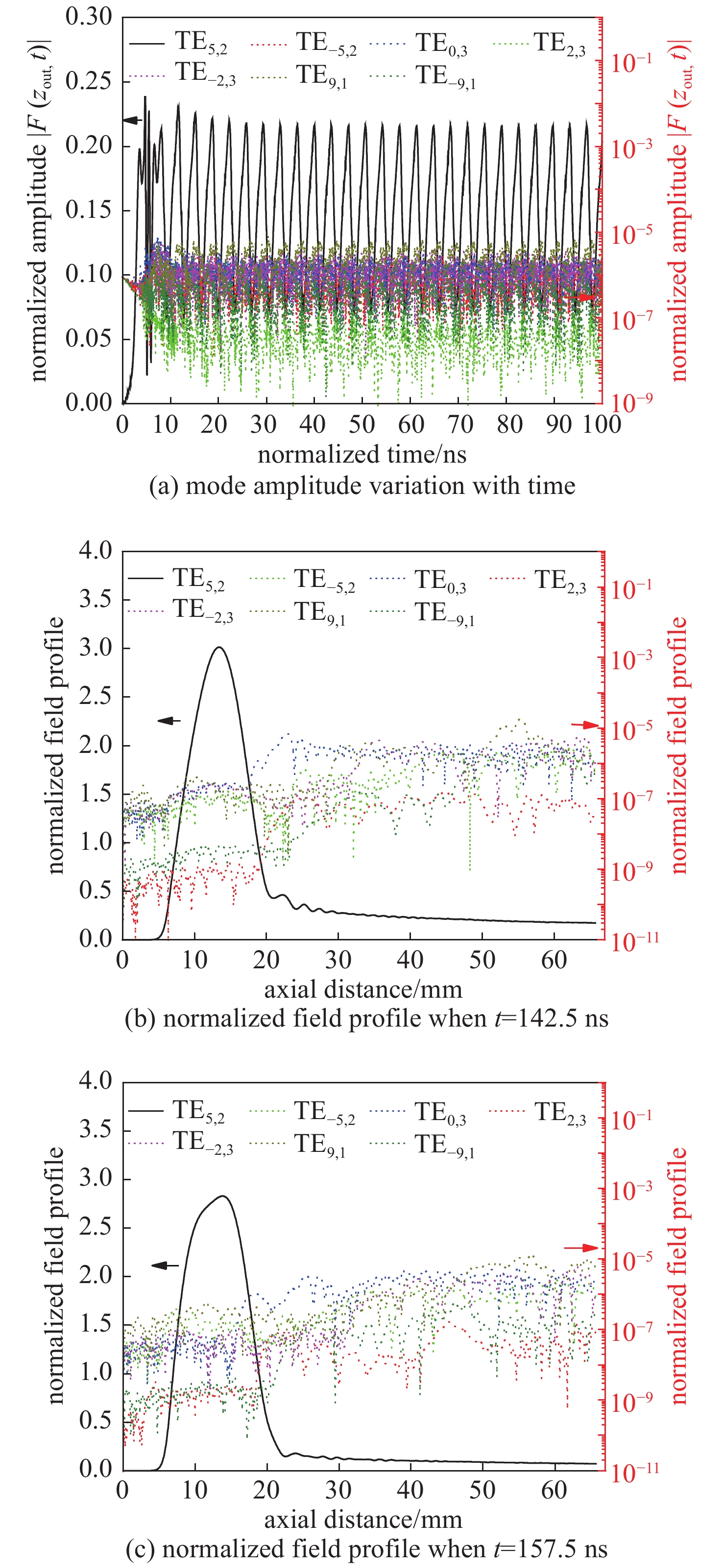
$ {\rm{\sigma }}=2.7\times {10}^{7} $ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}= 1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=35 $ mA)Figure 6. Nonstationary oscillation when
${\rm{\sigma }}=2.7\times {10}^{7}$ ,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}= 1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=35 $ mA;图 7 连续调谐回旋管稳定工作状态(
$ {\rm{\sigma }}=2.7\times {10}^{7} $ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=85 $ mA)Figure 7. Stationary oscillation when
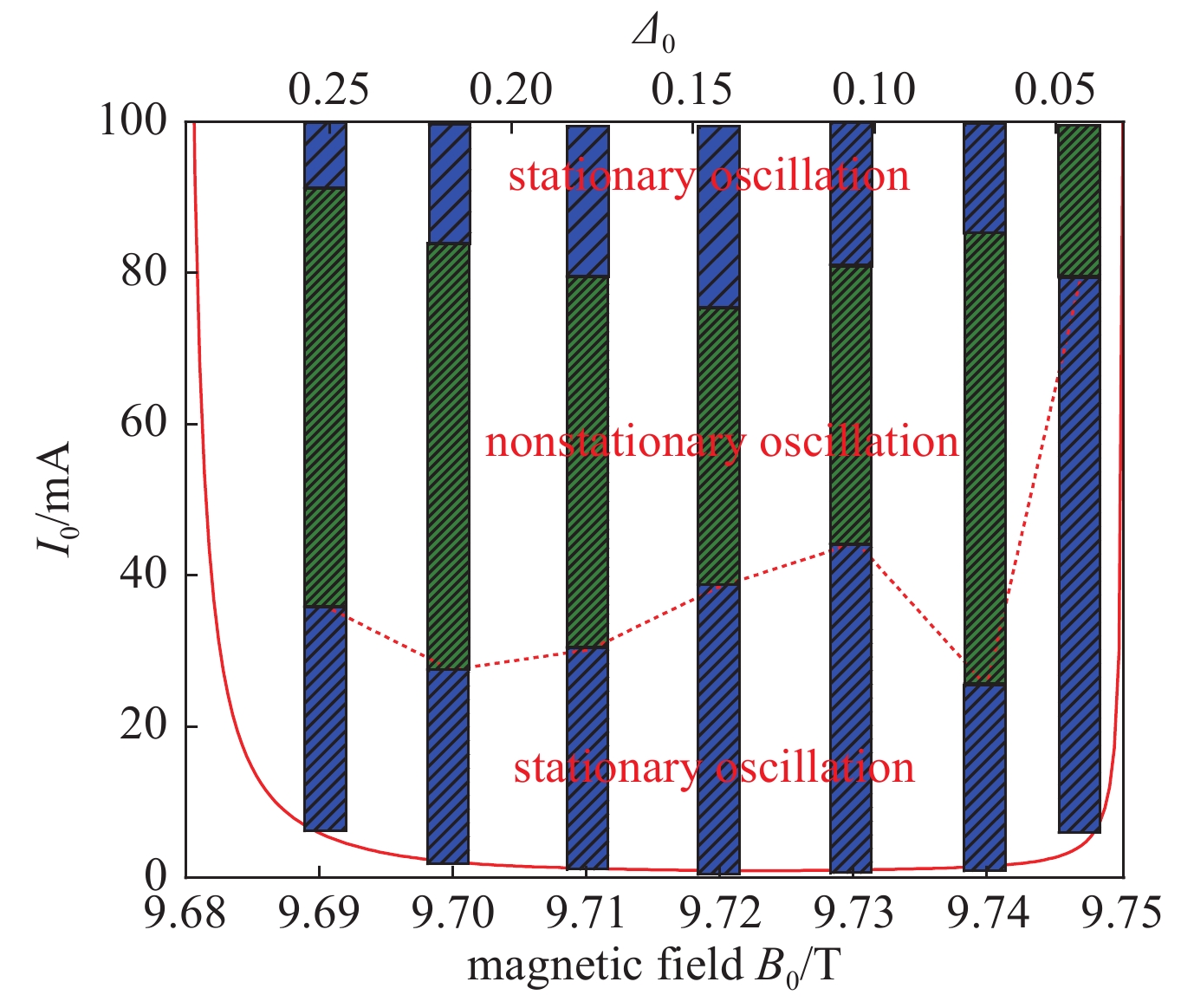
$ {\rm{\sigma }}=2.7\times {10}^{7} $ S/m,$ {U}_{0}= $ $ 20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ ,$ {B}_{0}=9.74 $ T,$ {I}_{0}=85 $ mA;图 8 非稳定振荡状态在磁场和电流平面上的分布(
${\rm{\sigma }}=2.7\times $ $ {10}^{7}$ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ )Figure 8. Categorization of non-stationary oscillation on plane of beam current and magnetic field (
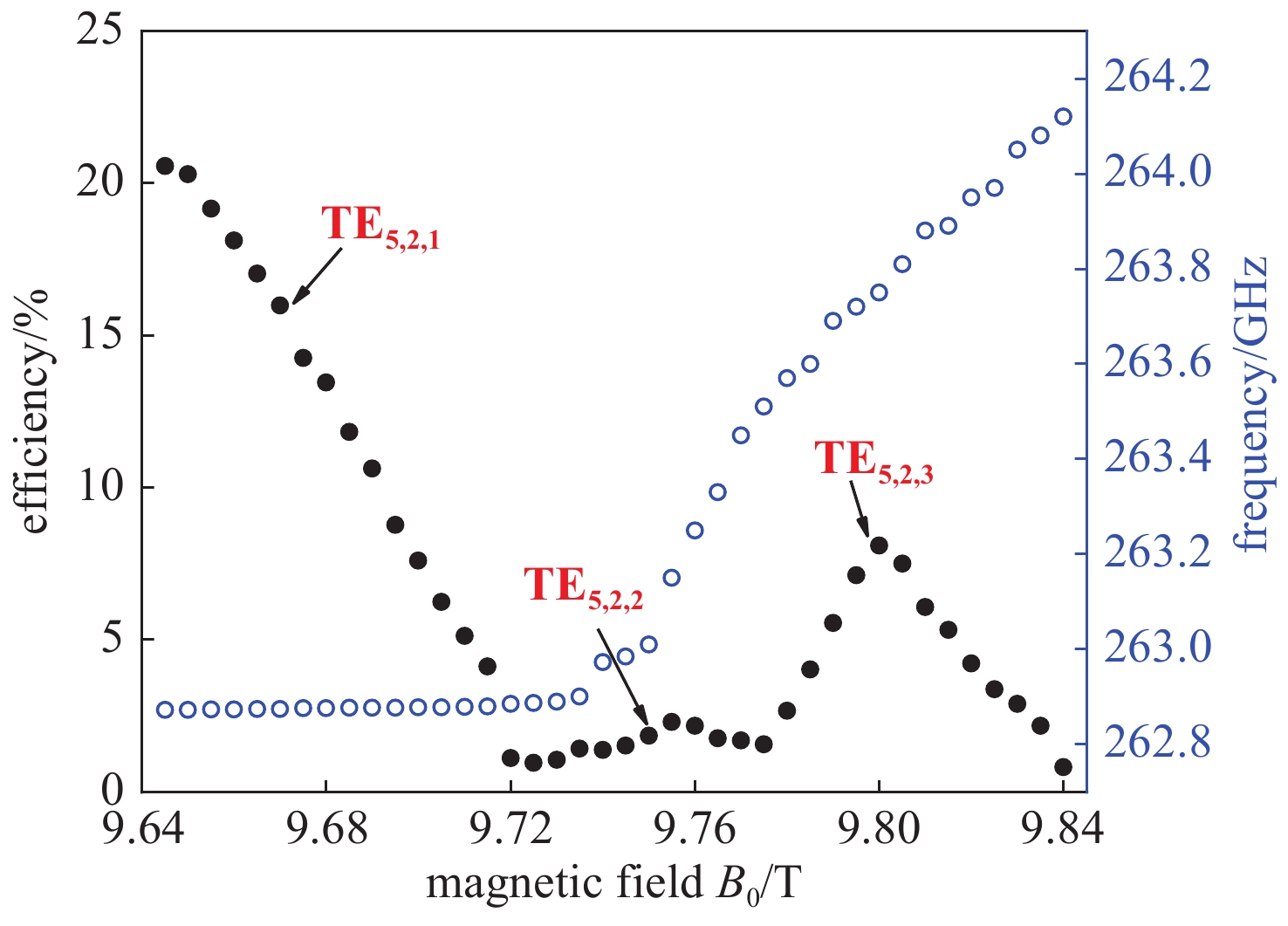
$ {\rm{\sigma }}=2.7\times {10}^{7} $ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {\rm{\alpha }}=1.75 $ )图 9 互作用效率和谐振频率随磁场的变化(
$ {\rm{\sigma }}=2.7\times $ $ {10}^{7} $ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {I}_{0}=20 $ mA)Figure 9. Beam wave interaction efficiency and oscillation frequency variation with magnetic field when
$ {\rm{\sigma }}=2.7\times {10}^{7} $ S/m,$ {U}_{0}=20 $ kV,$ {R}_{\rm{g}}=1.4 $ mm,$ {I}_{0}=20 $ mA表 1 263 GHz,
$ {\bf{TE}}_{{\bf{5,2}}} $ 基波连续调谐回旋管工作参数Table 1. Operating parameters for 263 GHz,
$ {\bf{TE}}_{\bf{{5,2}}} $ fundamental harmonic frequency continuously tunable gyrotronoperating
modebeam
current/mAbeam
voltage/kVguiding center
radius/mmpitch
factoroperating
frequency/GHzwall
conductivity/(S·m−1)frequency tunable
range/GHzpower tunable
range/W${\rm{TE} }_{5,2}$ 20 20 1.40 1.75 263 $ 2.7\times {10}^{7} $ 1.39 80 -
[1] Nanni E A, Barnes A B, Griffin R G, et al. THz dynamic nuclear polarization NMR[J]. IEEE Transactions onTerahertz Science and Technology, 2011, 1(1): 145-163. doi: 10.1109/TTHZ.2011.2159546 [2] Griffin R G, Prisner T F. High field dynamic nuclear polarization—the renaissance[J]. Physical Chemistry Chemical Physics, 2010, 12(22): 5737-5740. doi: 10.1039/c0cp90019b [3] Masion A, Alexandre A, Ziarelli F, et al. Dynamic Nuclear Polarization NMR as a new tool to investigate the nature of organic compounds occluded in plant silica particles[J]. Scientific Reports, 2017, 7: 3430. doi: 10.1038/s41598-017-03659-z [4] Liao S Y, Lee M, Wang T, et al. Efficient DNP NMR of membrane proteins: sample preparation protocols, sensitivity, and radical location[J]. Journal of Biomolecular NMR, 2016, 64(3): 223-237. doi: 10.1007/s10858-016-0023-3 [5] Leggett J, Hunter R, Granwehr J, et al. A dedicated spectrometer for dissolution DNPNMR spectroscopy[J]. Physical Chemistry Chemical Physics, 2010, 12(22): 5883-5892. doi: 10.1039/c002566f [6] Plainchont B, Berruyer P, Dumez J N, et al. Dynamic nuclear polarization opens new perspectives for NMR spectroscopy in analytical chemistry[J]. Analytical Chemistry, 2018, 90(6): 3639-3650. doi: 10.1021/acs.analchem.7b05236 [7] Mompeán M, Sánchez-Donoso R M, De LaHoz A, et al. Pushing nuclear magnetic resonance sensitivity limits with microfluidics and photo-chemically induced dynamic nuclear polarization[J]. Nature Communications, 2018, 9: 108. doi: 10.1038/s41467-017-02575-0 [8] 李志良, 冯进军, 蔡军. 太赫兹回旋管和动态核极化核磁共振的研究发展[J]. 真空科学与技术学报, 2015, 35(6):744-751. (Li Zhiliang, Feng Jinjun, Cai Jun. Latest progress of THz gyrotron and dynamic nuclear polarization enhanced nuclear magnetic resonance[J]. Chinese Journal of Vacuum Science and Technology, 2015, 35(6): 744-751 [9] 李志良, 冯进军, 刘本田, 等. DNP-NMR用263 GHz回旋振荡管高频系统的研究[J]. 真空科学与技术学报, 2017, 37(7):693-698. (Li Zhiliang, Feng Jinjun, Liu Bentian, et al. Circuit design of 263 GHz gyrotrono scillator for dynamic nuclear polarization enhanced nuclear magnetic resonance[J]. Chinese Journal of Vacuum Science and Technology, 2017, 37(7): 693-698 [10] 史少辉, 韩万强, 封顺珍, 等. 频率可调太赫兹回旋振荡管互作用电路的设计与研究[J]. 微波学报, 2020, 36(3):59-64. (Shi Shaohui, Han Wanqiang, Feng Shunzhen, et al. Investigation and design of a frequency-tunable terahertz gyrotron oscillator[J]. Journal of Microwaves, 2020, 36(3): 59-64 [11] 宋韬, 王维, 刘頔威, 等. 应用于动态核极化核磁共振的太赫兹回旋管[J]. 中国激光, 2019, 46:0614001. (Song Tao, Wang Wei, Liu Diwei, et al. Terahertz gyrotron used for dynamic nuclear-polarization-enhanced nuclear magnetic resonance[J]. Chinese Journal of Lasers, 2019, 46: 0614001 doi: 10.3788/CJL201946.0614001 [12] 雷蕾, 刘頔威, 鄢扬. 0.42 THz频率连续可调同轴回旋管[J]. 红外与毫米波学报, 2013, 32(6):559-562. (Lei Lei, Liu Diwei, Yan Yang. Continuous frequency tunable 0.42 THz coaxial gyrotron[J]. Journal of Infrared and Millimeter Waves, 2013, 32(6): 559-562 doi: 10.3724/SP.J.1010.2013.00559 [13] Temkin R J. Development of terahertz gyrotrons for spectroscopy at MIT[J]. Terahertz Science and Technology, 2014, 7(2): 1-9. [14] Hornstein M K, Bajaj V S, Griffin R G, et al. Design of a 460 GHz second harmonic gyrotron oscillator for use in dynamic nuclear polarization[C]//Proceedings of the Twenty Seventh International Conference on Infrared and Millimeter Waves. San Diego: IEEE, 2002: 193-194. [15] Idehara T, Kosuga K, Agusu L, et al. Continuously frequency tunable high power sub-THz radiation source—gyrotron FU CW VI for 600 MHz DNP-NMR spectroscopy[J]. Journal ofInfrared, Millimeter, and Terahertz Waves, 2010, 31(7): 775-790. doi: 10.1007/s10762-010-9643-y [16] Glyavin M Y, Chirkov A V, Denisov G G, et al. Experimental tests of a 263 GHz gyrotron for spectroscopic applications and diagnostics of various media[J]. Review ofScientific Instruments, 2015, 86: 054705. doi: 10.1063/1.4921322 [17] Yoon D, Soundararajan M, Cuanillon P, et al. Dynamic nuclear polarization by frequency modulation of a tunable gyrotron of 260 GHz[J]. Journal of Magnetic Resonance, 2016, 262: 62-67. doi: 10.1016/j.jmr.2015.11.008 [18] Braunmüller F. Gyrotron physics from linear to chaotic regimes: experiment and numerical modeling[D]. Lausanne: École Polytechnique Fédérale de Lausanne, 2016: 50-76. [19] Airila M I, Dumbrajs O, Reinfelds A, et al. Nonstationary oscillations in gyrotrons[J]. Physicsof Plasmas, 2001, 8(10): 4608-4612. doi: 10.1063/1.1402173 [20] Kern S. Numerische simulation der gyrotron-wechselwirkung in koaxialen resonatoren[D]. Karlsruhe: Universität Karlsruhe, 1996. [21] Kartikeyan M V, Borie E, Thumm M K A. Gyrotrons— high power microwave and millimeter wave technology[M]. Berlin: Springer Press, 2003. [22] Dumbrajs O, Nusinovich G S. Self-consistent non-stationary theory of the gyrotron[J]. Physics of Plasmas, 2016, 23: 083125. doi: 10.1063/1.4961962 [23] Li Zhengdi, Du Chaohai, Qi Xiangbo, et al. A 0.33-THz second-harmonic frequency-tunable gyrotron[J]. Chinese Physics B, 2016, 25: 029401. [24] Zhao Qixiang, Yu Sheng, Zhang Yanyan, et al. Investigation of the influence of electron beam quality on the operation in 0.42-THz second harmonic gyrotron[J]. IEEE Transactions on Plasma Science, 2016, 44(5): 749-754. doi: 10.1109/TPS.2016.2551734 [25] 张延庆. 频率超宽带连续可调太赫兹回旋管电子枪研究[D]. 成都: 电子科技大学, 2020.Zhang Yanqing. Research on magnetron injected gun of a ultra-wideband continuously adjustable terahertz gyrotron[D]. Chengdu: University of Electronic Science and Technology of China, 2020 [26] 刘冲, 赵青, 胡以怀, 等. 双注磁控注入电子枪[J]. 强激光与粒子束, 2014, 26:083005. (Liu Chong, Zhao Qing, Hu Yihuai, et al. Double-beam magnetron injection gun[J]. High Power Laser and Particle Beams, 2014, 26: 083005 doi: 10.11884/HPLPB201426.083005 -




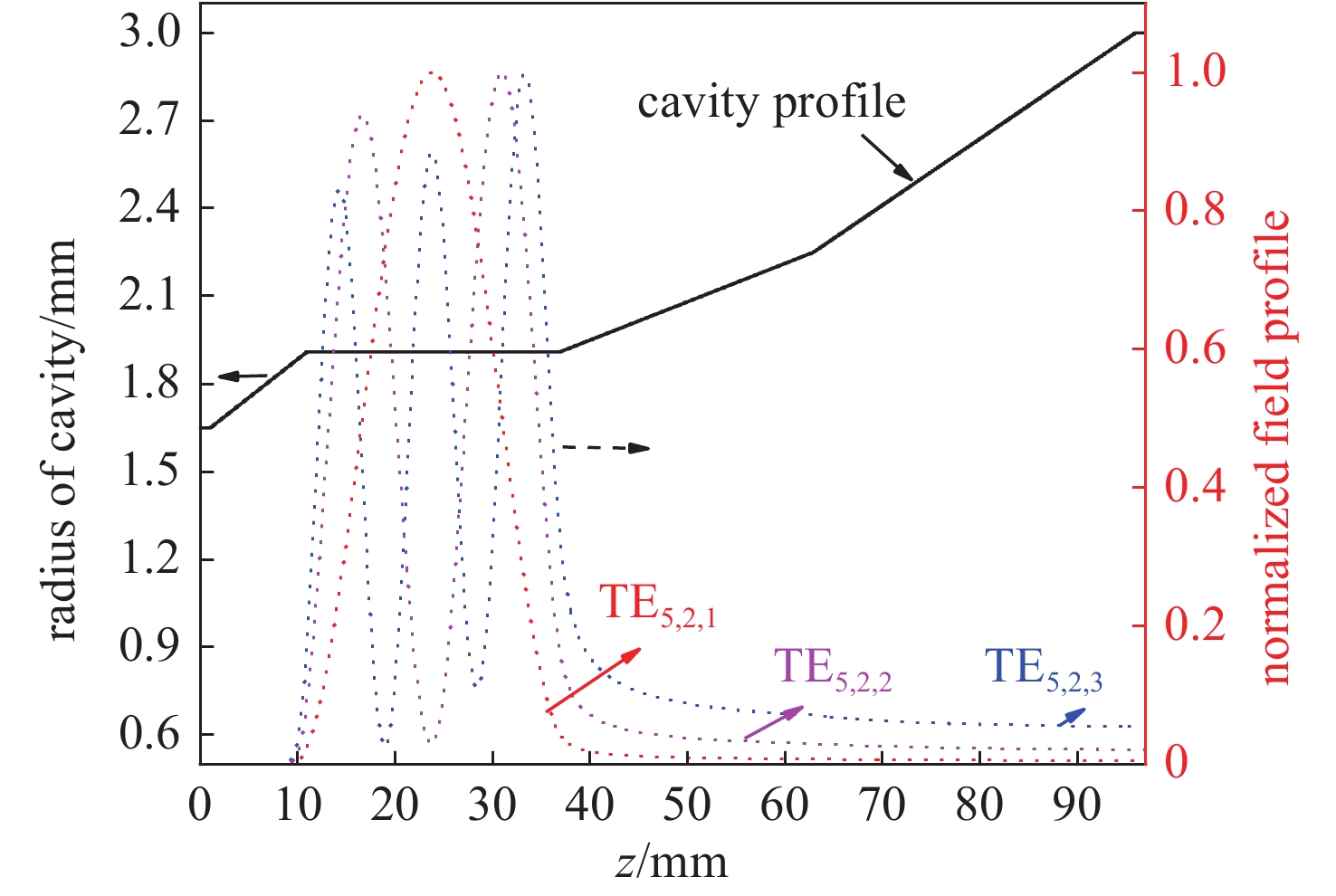
 下载:
下载: