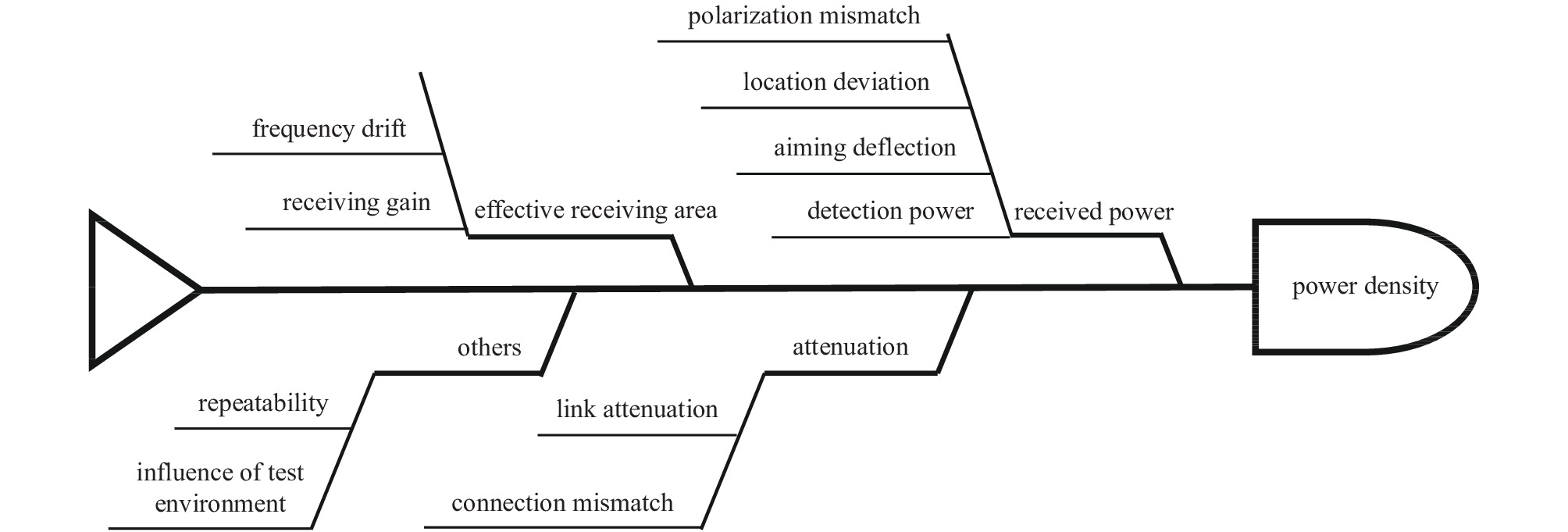
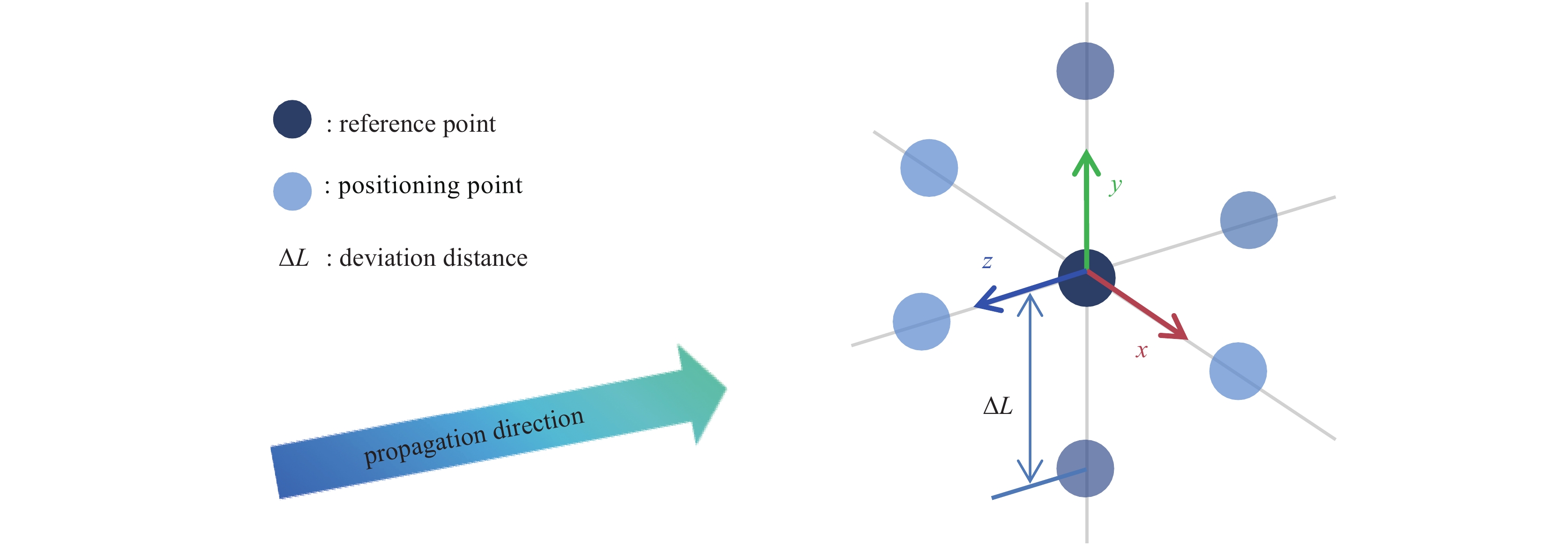
Evaluation of measurement uncertainty about power density for high power microwave effects test
-
摘要: 针对窄带高功率微波（HPM）效应试验的辐射场准确测试需求，分析补充了功率密度参数的测量不确定度主要分量，提出了一个参数更为全面的乘式测量不确定度评估模型。采用B类评估方法，根据相关标准和信息对各分量进行了一组赋值，计算得到了相对形式的分量标准不确定度。给出了评估测试环境影响、位置偏差等分量不确定度半宽度的实验方法，为HPM效应功率密度参数测量不确定度的合理评定提供了参考，为实现其全部分量基于实测数据客观评估测量不确定度提供了操作方法。Abstract: For the requirement of accurate measurement of radiation field in narrow band high power microwave (HPM) effects test, the quantities of measurement uncertainty about power density were analyzed and supplemented. A multiplicative and comprehensive model of measurement uncertainty was derived. On the basis of set values according to relating standards and information, the evaluation of quantity standard uncertainty in relative form was realized by using type B method. Besides, measurement evaluation method was given for quantities of influence of test environment and location deviation. This work provides a reference for reasonable evaluation of measurement uncertainty of power density parameters of HPM effect and an operation method for objective evaluation of measurement uncertainty of all components based on measured data.
-
图 2 功率密度测量不确定度输入分量关系鱼骨图
Figure 2. Fish bone diagram of input quantities for power density measurement uncertainty
图 3 环境影响分量测试评估布设示意图
Figure 3. Measurement evaluation layout for quantity of influence of test environment
图 4 位置偏差测试评估布设示意图
Figure 4. Measurement evaluation layout for quantity of location deviation
表 1 HPM效应测试中功率密度参数测量不确定度B类评定参数
Table 1. Type B evaluation parameters of measurement uncertainty about power density for high power microwave effects test
uncertainty quantity distribution k-value sensitivity coefficient relative standard uncertainty/dB relative standard uncertainty/% detection power ${P_{ {\text{det} } } }$ triangular $ \sqrt{6} $ 1 0.46 10.58 link attenuation $ {A'} $ normal 2 1 1.20 27.60 receiving gain $ {G_{\text{r}}} $ rectangular $ \sqrt{3} $ −1 0.87 19.92 location deviation $ {A_{\text{l}}} $ rectangular $ \sqrt{3} $ 1 0.14 3.31 frequency drift $ f $ rectangular $ \sqrt{3} $ 2 0.06 1.41 aiming deflection $ {A_{\text{d}}} $ rectangular $ \sqrt{3} $ 1 0.14 3.31 polarization mismatch ${A_{\text{P}}}$ rectangular $ \sqrt{3} $ 1 0.15 3.54 connection mismatch $ {A_{\text{c}}} $ arc sine $ \sqrt{2} $ 1 0.21 4.83 influence of test environment $ {A_{{\text{te}}}} $ rectangular $ \sqrt{3} $ 1 1.22 28.06 repeatability $ {C_{\text{r}}} $ normal 2 1 0.13 2.89 
下载: 导出CSV
-
[1] GJB 8385-2015, 军用电子系统窄带高功率微波注入法效应试验规程[S]GJB 8385-2015, Test specifications of injection method for narrow-band HPM effects on military electronic systems[S] [2] GJB 8848-2016, 系统电磁环境效应试验方法[S]GJB 8848-2016, Electromagnetic environmental effects test methods for systems[S] [3] GJB 9257-2017, 高功率微波效应试验方法 窄带高功率微波辐照法[S]GJB 9257-2017, Test method for high power microwave effects: narrow band high power microwave radiation method[S] [4] GJB 9896-2020, 高功率微波效应试验方法 超宽带高功率微波辐照法[S]GJB 9896-2020, Test method for high power microwave effects: ultra wide band high power microwave radiation method[S] [5] GJB 9382-2018, 窄谱高功率微波功率测量方法[S]GJB 9382-2018, The method of power measurement for narrow band high power microwave[S] [6] 刘英君, 晏峰, 景洪, 等. 高功率微波辐射场功率密度测量不确定度分析方法[J]. 电波科学学报, 2017, 32(4):398-402. (Liu Yingjun, Yan Feng, Jing Hong, et al. Measurement uncertainty on power density of high power microwave radiation[J]. Chinese Journal of Radio Science, 2017, 32(4): 398-402 [7] 张伟伟, 杨绪军, 陈云梅. 相对测量不确定度在微波功率计量中的应用[J]. 宇航计测技术, 2015, 35(5):1-5. (Zhang Weiwei, Yang Xujun, Chen Yunmei. Application of relative measurement uncertainty in microwave power measurement[J]. Journal of Astronautic Metrology and Measurement, 2015, 35(5): 1-5 doi: 10.3969/j.issn.1000-7202.2015.05.001 [8] 倪育才. 实用测量不确定度评定[M]. 3版. 北京: 中国计量出版社, 2009: 70Ni Yucai. Practical evaluation of measurement uncertainty[M]. 3rd ed. Beijing: China Metrology Press, 2009: 70 [9] ZWB 475-2016, 微波检波器校准规程[S]ZWB 475-2016, Calibration specification for microwave detector[S] [10] 刘钰, 韩峰, 陆希成, 等. 基于回归分析的检波器标定实验测量不确定度评定[J]. 现代应用物理, 2013, 4(3):303-306. (Liu Yu, Han Feng, Lu Xicheng, et al. Uncertainty analysis in detector calibration experiments based on regression[J]. Modern Applied Physics, 2013, 4(3): 303-306 doi: 10.3969/j.issn.2095-6223.2013.03.016 [11] 成真伯, 刘小龙, 闫军凯. 蒙特卡罗方法评定峰值检波器标定不确定度[J]. 强激光与粒子束, 2016, 28:113007. (Cheng Zhenbo, Liu Xiaolong, Yan Junkai. Evaluation of uncertainty in peak detector calibration based on Monte-Carlo method[J]. High Power Laser and Particle Beams, 2016, 28: 113007 doi: 10.11884/HPLPB201628.151066 [12] CNAS GL026-2018, 无线电领域测量不确定度评估指南及实例[S]CNAS GL026-2018, Guidance and illustration on evaluating the uncertainty in radio field[S] [13] 蒋廷勇, 高林, 刘小龙, 等. 抑制地面反射影响的高功率微波辐射场测量方法[J]. 强激光与粒子束, 2015, 27:123007. (Jiang Tingyong, Gao Lin, Liu Xiaolong, et al. Minimizing the impact of ground reflection on high power microwave E-field measurement[J]. High Power Laser and Particle Beams, 2015, 27: 123007 doi: 10.11884/HPLPB201527.123007 [14] GB/T 6113.402-2018, 无线电骚扰和抗扰度测量设备和测量方法规范 第4-2部分: 不确定度、统计学和限值建模 测量设备和设施的不确定度[S]GB/T 6113.402-2018, Specification for radio disturbance and immunity measuring apparatus and methods—Part 4-2: Uncertainties, statistics and limit modelling—Measurement instrumentation uncertainty[S] [15] JJF 1059.1-2012, 测量不确定度评定与表示[S]JJF 1059.1-2012, Evaluation and expression of uncertainty in measurement[S] -
点击查看大图
图(4) / 表(2)
计量
- 文章访问数: 1068
- HTML全文浏览量: 358
- PDF下载量: 95
- 被引次数: 0
