Uncertainty analysis method of induced voltage of transmission line based on interval
-
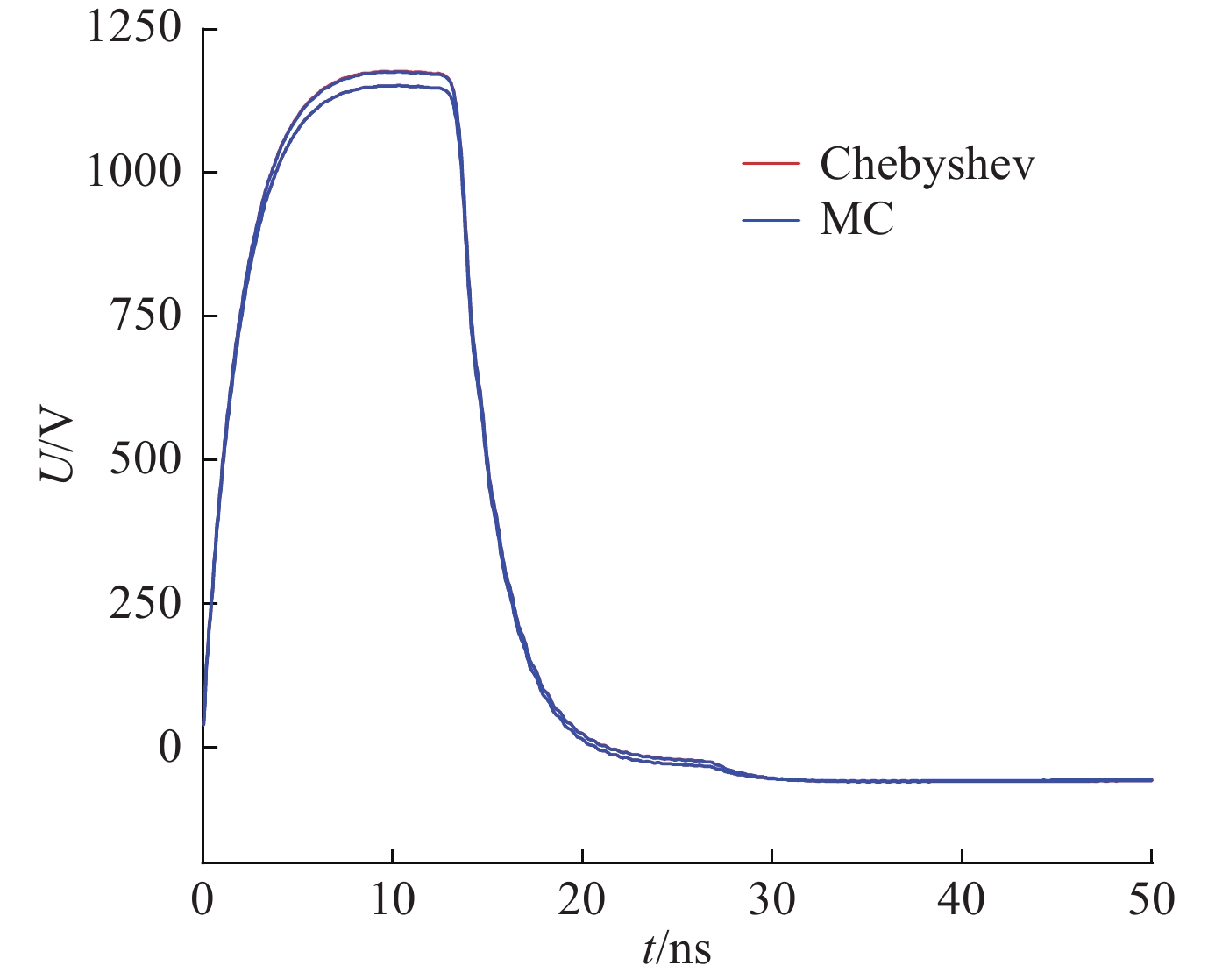
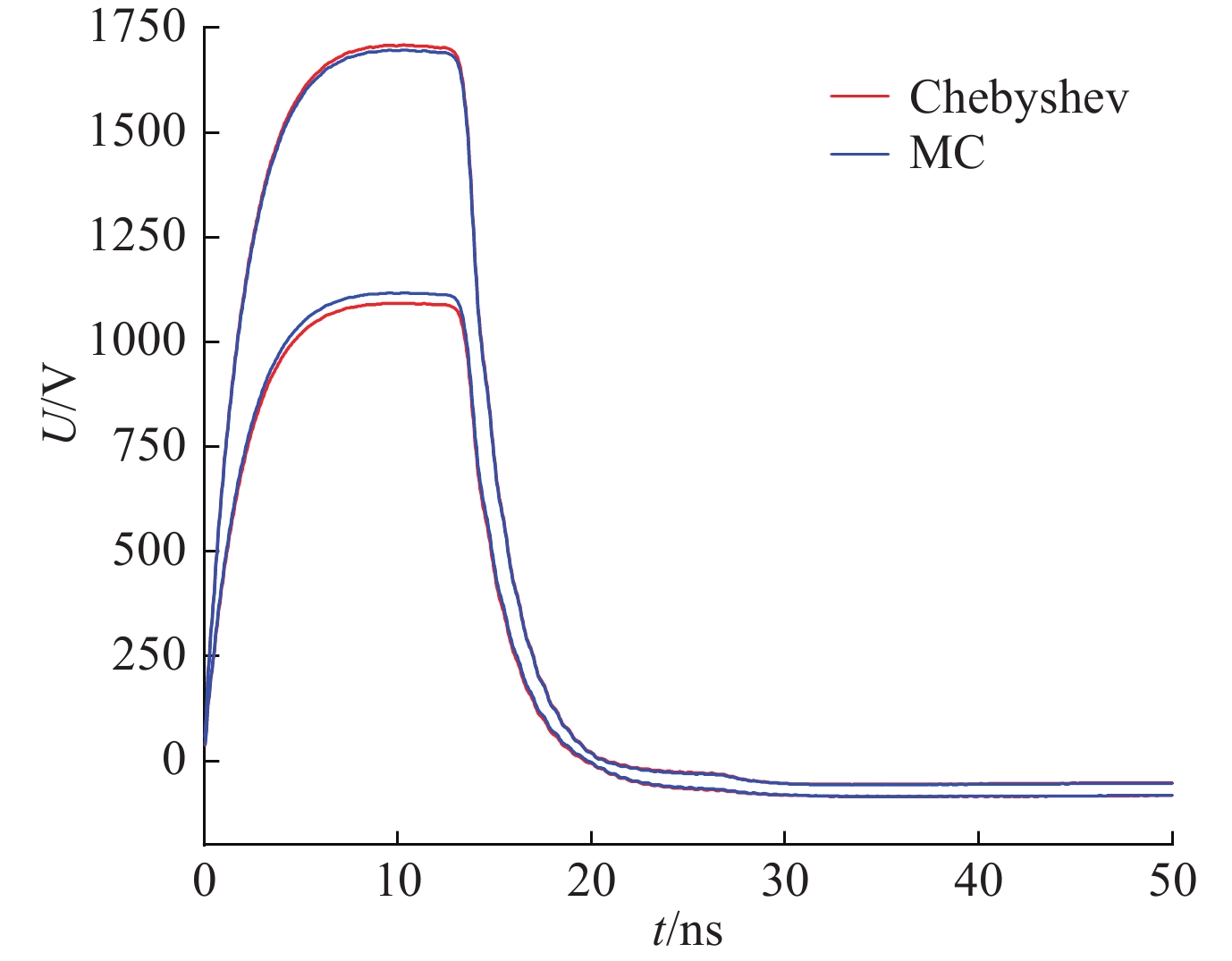
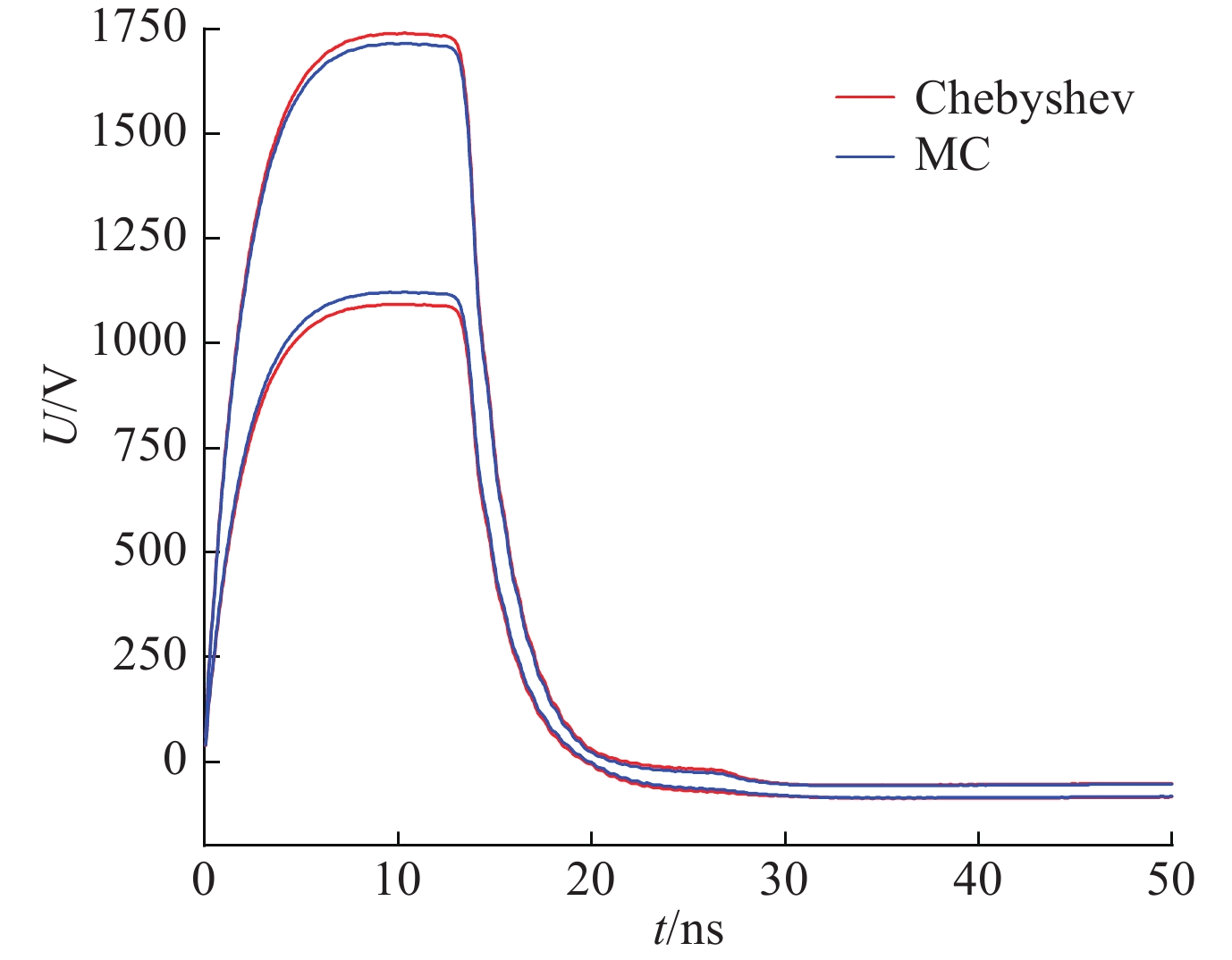
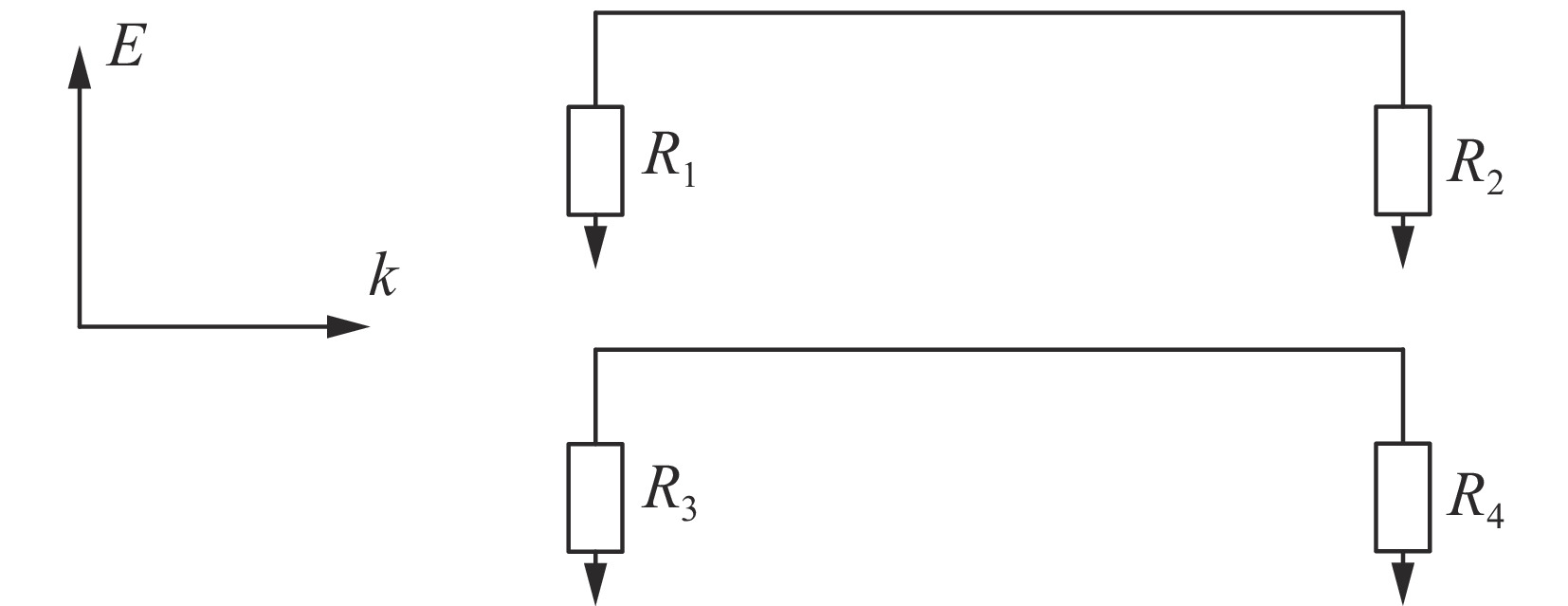
摘要: 为分析多导体传输线耦合情况下线缆结构参数的不确定性对终端电压的影响,引入了一种基于区间分析的切比雪夫(Chebyshev)多项式逼近方法。该方法首先将传输线电报方程转换为常微分方程求解;其次采用Chebyshev多项式求得电报方程的扩张函数,进而获得终端电压的波动范围。相比于混沌多项式方法和蒙特卡罗(MC)法,此方法只需要输入随机参数的波动范围。针对电磁脉冲辐照下高度和间距随机变动的多导体线束进行仿真,仿真结果表明,间距基本不影响终端电压,终端电压对高度更为敏感。在计算结果基本一致的情况下,Chebyshev多项式逼近方法的计算耗时远小于MC方法。Abstract: To analyze the effect of the uncertainty of cable structure parameters on terminal voltage under the coupling of multi-conductor transmission lines, a method of Chebyshev polynomial approximation based on interval analysis is introduced. Firstly, the telegraph equation of transmission line is transformed into an ordinary differential equation. Secondly, the extension function of the telegraph equation is obtained by Chebyshev polynomial, and then the fluctuation range of terminal voltage is obtained. Compared with the mixed polynomial method and MC (Monte Carlo) method, this method only needs to input the range of fluctuation of random parameters. The multi-conductor wire beam with random variation of height and spacing under electromagnetic pulse irradiation was simulated. The simulation results show that the distance has little effect on terminal voltage, and the terminal voltage is more sensitive to height. Under the condition that the calculated results are in agreement with each other, the computation time of Chebyshev polynomial approximation method is much less than that of MC method.
-
Key words:
- interval analysis /
- multiconductor transmission line /
- uncertainty /
- Monte Carlo method
-
表 1 MC方法与Chebyshev多项式逼近方法的计算耗时
Table 1. Time consuming computation of MC method and Chebyshev polynomial approximation method
item calculation time/s random d,h random d random h MC 7492 7381 7430 Chebyshev 490 22 67 -
[1] 刘尚合, 刘卫东. 电磁兼容与电磁防护相关研究进展[J]. 高电压技术, 2014, 40(6):1605-1613. (Liu Shanghe, Liu Weidong. Progress of relevant research on electromagnetic compatibility and electromagnetic protection[J]. High Voltage Engineering, 2014, 40(6): 1605-1613 [2] 谢彦召, 王赞基, 王群书, 等. 高空核爆电磁脉冲波形标准及特征分析[J]. 强激光与粒子束, 2003, 15(8):781-787. (Xie Yanzhao, Wang Zanji, Wang Qunshu, et al. High altitude nuclear electromagnetic pulse waveform standards: a review[J]. High Power Laser and Particle Beams, 2003, 15(8): 781-787 [3] 杨春山, 程柏林. 雷电电磁脉冲对电缆的耦合效应研究[J]. 空军雷达学院学报, 2005, 19(2):1-5. (Yang Chunshan, Cheng Bolin. Study of coupling effects of lightning electromagnetic pulse on cable[J]. Journal of Air Force Radar Academy, 2005, 19(2): 1-5 [4] 孙丹峰, 季幼章. 雷电的危害及实例分析[J]. 电源世界, 2016(1):52-57. (Sun Danfeng, Ji Youzhang. The harm and the example analysis of lightning[J]. The World of Power Supply, 2016(1): 52-57 [5] 齐磊. 多导体传输线的时域有限差分法研究[D]. 保定: 华北电力大学(河北), 2003: 18-22Qi Lei. Research of the multi-conductor transmission lines with the finite difference-time domain method[D]. Baoding: North China Electric Power University (Hebei), 2003: 18-22 [6] 齐磊, 卢铁兵, 张重远, 等. 考虑多层土壤时架空线的瞬态分析[J]. 中国电机工程学报, 2003, 23(5):66-69. (Qi Lei, Lu Tiebing, Zhang Zhongyuan, et al. Transient analysis of overhead lines with multi-layer soil[J]. Proceedings of the CSEE, 2003, 23(5): 66-69 doi: 10.3321/j.issn:0258-8013.2003.05.015 [7] 卢铁兵, 崔翔. 有损土壤上的多导体传输线的时域分析[J]. 电波科学学报, 2000, 15(3):269-274. (Lu Tiebing, Cui Xiang. FDTD analysis of multi conductor transmission lines over lossy ground[J]. Chinese Journal of Radio Science, 2000, 15(3): 269-274 doi: 10.3969/j.issn.1005-0388.2000.03.004 [8] 焦重庆, 汪贝, 李昱蓉, 等. 用于半波长输电线路的精细化传输线模型[J]. 高电压技术, 2018, 44(1):3-13. (Jiao Chongqing, Wang Bei, Li Yurong, et al. Refined transmission line model for half-wavelength transmission lines[J]. High Voltage Engineering, 2018, 44(1): 3-13 [9] 张希. 有损均匀传输线数值解的研究[D]. 重庆: 重庆大学, 2003: 42-59Zhang Xi. Rearch on lossy and uniform transmission line unmerical solution[D]. Chongqing: Chongqing University, 2003: 42-59 [10] 王旭桐, 周辉, 马良, 等. 传输线方程的高精度龙格-库塔数值求解方法[J]. 强激光与粒子束, 2020, 32:033202. (Wang Xutong, Zhou Hui, Ma Liang, et al. High-precision Runge-Kutta method for transmission line equation[J]. High Power Laser and Particle Beams, 2020, 32: 033202 [11] 张瑛, Wang J M, 肖亮, 等. 工艺参数随机扰动下的传输线建模与分析新方法[J]. 电子学报, 2005, 33(11):1959-1964. (Zhang Ying, Wang J M, Xiang Liang, et al. A new stochastic modeling and analysis method for transmission lines in the presence of random process variations[J]. Acta Electronica Sinica, 2005, 33(11): 1959-1964 doi: 10.3321/j.issn:0372-2112.2005.11.010 [12] 程市, 黄斌科, 师振盛. 一种分析微带线随机参数敏感性的多项式混沌展开方法[J]. 西安交通大学学报, 2016, 50(12):121-127. (Cheng Shi, Huang Binke, Shi Zhensheng. A polynomial chaos expansion method for sensitivity analysis of microstrip transmission lines with stochastic parameters[J]. Journal of Xi’an Jiaotong University, 2016, 50(12): 121-127 [13] 吴景铼. 基于Chebyshev多项式的动力学不确定性区间算法研究[D]. 武汉: 华中科技大学, 2013: 53-58Wu Jinglai. Dynamics uncertainty research based on interval arithmetic using Chebyshev polynomials[D]. Wuhan: Huazhong University of Science and Technology, 2013: 53-58 [14] 魏莎. 含区间不确定性参数的风电齿轮传动系统动力学特性研究[D]. 北京: 清华大学, 2015: 52-60Wei Sha. Studies on dynamic characteristics of wind turbine geared transmission system with interval uncertain parameters[D]. Beijing: Tsinghua University, 2015: 52-60 [15] 魏莎, 韩勤锴, 褚福磊. 考虑不确定参数的齿轮副非线性动态特性分析[J]. 振动与冲击, 2016, 35(10):44-48,59. (Wei Sha, Han Qinkai, Chu Fulei. Nonlinear dynamic analysis of gear-pair systems with uncertainties[J]. Journal of Vibration and Shock, 2016, 35(10): 44-48,59 -




 下载:
下载: