氘钛等离子体高压查尔特鞘层特性理论研究

沈伯昊; 董烨; 周前红; 杨温渊; 董志伟

doi:10.11884/HPLPB202234.210457

氘钛等离子体高压查尔特鞘层特性理论研究

doi: 10.11884/HPLPB202234.210457

沈伯昊^{1, 2,},
董烨^1, ,,
周前红¹,
杨温渊¹,
董志伟¹

1.
北京应用物理与计算数学研究所, 北京 100094
2.
中国工程物理研究院研究生部, 北京 100088

基金项目: 国家自然科学基金项目（11875094）；国家自然科学基金委员会与中国工程物理研究院联合基金项目（U1730247）

详细信息

作者简介:
沈伯昊，shenbohao20@gscaep.ac.cn

通讯作者:
董　烨，dongye0682@sina.com

中图分类号: TN752.5
计量
- 文章访问数: 735
- HTML全文浏览量: 247
- PDF下载量: 48
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-30
- 修回日期: 2022-01-17
- 网络出版日期: 2022-07-04
- 刊出日期: 2022-05-12

Theoretical study on characteristics of high voltage Child-sheath of mixed D⁺ and Ti²⁺ plasmas

1.
Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
2.
Graduate School of China Academy of Engineering Physics, Beijing 100088, China

摘要

摘要: 建立了混合多组分等离子体高压查尔特鞘层动力学模型，数值研究了氘钛等离子体高压查尔特鞘层特性。理论与数值研究结果表明，提升D⁺离子比例、降低D⁺离子及Ti²⁺离子入鞘速度、降低等离子体密度等方式，均会有效增加鞘层厚度，并降低靶面场强幅值，这些方式有利于离子汇聚传输和降低靶面击穿风险。随加速电压的增加，离子引出稳定工作区域范围呈现先增加后减小的趋势。增加D⁺离子比例、减小D⁺离子及Ti²⁺离子入鞘速度，均会显著增加离子引出稳定工作区域范围。
- 混合多组分等离子体 /
- 高压查尔特鞘层 /
- 动力学模型
Abstract: A dynamic model for high voltage Child-sheath of mixed multi-component plasmas is built up, and the characteristics of high voltage Child-sheath of mixed D⁺ and Ti²⁺ plasmas is numerically studied. The theoretical and numerical results demonstrate as follows. The depth of Child-sheath will increase and electric field intensity on target will decrease by increasing the ratio of D⁺ to Ti²⁺, decreasing the sheath-entering velocity of D⁺ or Ti²⁺, and decreasing the density of mixed plasmas. Through the above ways, ions could achieve convergent transportation and breakdown risk on target could also be reduced. As the increase of accelerating voltage, the range of stable ion-extraction operating region will firstly increase and then decrease. By increasing the ratio of D⁺ to Ti²⁺ and decreasing the sheath-entering velocity of D⁺ or Ti²⁺, the range of stable ion-extraction operating region could be notably increased.
- mixed multi-component plasmas /
- high voltage Child-sheath /
- dynamic model

HTML全文

真空弧离子源具有结构简单、不需充气和外加磁场约束的优势，可产生高密度等离子体，广泛应用于工业镀膜、真空开关、空间电推进等诸多领域^[1-4]。离子源要加以利用，就必须使用高电压将离子从中性等离子体区引出，其引出机理是由等离子体发射特性和空间限制流限制双重机制决定的^[5-6]。离子从等离子中性区边界到靶面区域的特性极为重要，这个区域就是高压等离子鞘层。它又分为板形鞘层和查尔特鞘层，由于板形鞘层假定鞘层内离子密度均匀分布，因此其只能瞬态存在并不能达到稳态；而查尔特鞘层是高压鞘层趋于稳态的形式^[7]，因此，研究它更具价值和实际意义。

目前，研究工作主要集中于单组分离子高压鞘层，Riemann，Benilnov等人开展了解析理论研究^[8-9]；针对金属离子超声速运动的高压鞘层特性，Brown研究了考虑离子漂移速度的单组分等离子体高压鞘层特性^[10]；Anders计算了单组分铝离子高压等离子体鞘层厚度与基片场强关系^[11]；Bilek计算获得了金属单组分等离子体板形鞘层及查尔特鞘层稳定工作区、击穿区以及等离子体耗损区^[12]。国内陈磊等人开创性地开展了混合离子束真空弧等离子体鞘层特性理论研究，研究了固定组分比例、固定离子入鞘速度条件下氘钛混合离子的高压鞘层特性^[13]。实际应用中，含氢金属电极真空弧放电过程中产生的混合组分氘钛等离子体状态较为复杂，需要对多种复杂可变因素下的高压鞘层特性进行快速理论评估。

基于上述应用背景，本文建立了更具普适意义的混合多组分等离子体高压查尔特鞘层动力学物理模型，原则上适用于任意多种离子组分构成的无碰撞等离子体，且各离子组分比例可变、各离子入鞘速度可变。此外，利用建立的动力学模型，数值研究了多因素影响下氘钛混合等离子体高压查尔特鞘层特性，可为离子引出及材料改性方面的应用提供理论依据和参考。

1. 混合多组分等离子体高压查尔特鞘层的动力学建模

真空弧离子源放电后产生的混合多组分等离子体，需要使用高电压将离子引出，这个高电压区基本上只有多组分离子的存在，而电子则被抑制在这个高压鞘层之外的中性等离子体区域。等离子体发射面会根据等离子体发射特性和空间限制流限制双重机制进行动态调节，当发射面的场强和电位近似为零时，鞘层状态达到稳定。此时的高压鞘层称为高压查尔特鞘层，其中性等离子体区无碰撞等离子体。为建立混合多组分等离子体高压查尔特鞘层动力学模型，首先需要确定多组分离子的入鞘速度关系，其次需要利用边界条件对静电泊松方程进行定解，来完整获得多组分离子高压查尔特鞘层的动力学模型。

1.1 多组分离子入鞘速度的确定

假设等离子体由 $N$ 种正离子和电子构成，其中，第m种离子（ $m = 1,\;2,\; \cdots ,\;N$ ）的电荷量为 $+ {q_m}$ ，质量为 ${M_m}$ ；电子电荷量为 $- e$ 。由等离子体中性区与鞘层交界面的准电中性特性可得

$\displaystyle\sum\limits_{m = 1}^N {{q_m}{n_{{\rm{s}}m}}} = e{n_{{\rm{se}}}}$

(1)

式中： ${n_{{\rm{s}}m}}$ 为中性区与鞘层交界面处第m种离子密度； ${n_{{\rm{se}}}}$ 为中性区与鞘层交界面处的电子密度。

无碰撞情况下，由离子能量守恒，可得

$\begin{array}{*{20}{c}} {\dfrac{1}{2}{M_m}u_m^2\left( x \right) = \dfrac{1}{2}{M_m}u_{{\rm{s}}m}^2 - {q_m}{\mathit{\Phi}} \left( x \right)}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(2)

式中： ${u_{{\rm{s}}m}}$ 为中性区与鞘层交界面第m种离子的速度；边界面位置设为 $x = 0$ ，边界面电位 ${\mathit{\Phi}} \left( 0 \right) = 0$ ， ${\mathit{\Phi}} \left( x \right)$ 为鞘层区域电位分布。鞘层区域 $x \geqslant 0$ ，式（2）求解区域 ${\mathit{\Phi}} \left( x \right) \leqslant 0$ 。

假设在鞘层中无电离过程发生，由各组分离子通量连续性，可得

$\begin{array}{*{20}{c}} {{n_m}\left( x \right){u_m}\left( x \right) = {n_{{\rm{s}}m}}{u_{{\rm{s}}m}}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(3)

式中： ${n_m}\left( x \right)$ 和 ${u_m}\left( x \right)$ 分别为鞘层区域第m种离子的密度和速度。

将式（2）代入式（3），可得

$\begin{array}{*{20}{c}} {{n_m}\left( x \right) = {n_{{\rm{s}}m}}{{\left( {1 - \dfrac{{2{q_m}{\mathit{\Phi}} \left( x \right)}}{{{M_m}u_{{\rm{s}}m}^2}}} \right)}^{ - 1/2}}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(4)

电子密度可由玻耳兹曼关系式给出

${n_{\rm{e}}}\left( x \right) = {n_{{\rm{se}}}}\exp \left( {{{\mathit{\Phi}} \mathord{\left/ {\vphantom {{\mathit{\Phi}} {{T_e}}}} \right. } {{T_{\rm{e}}}}}} \right)$

(5)

式中： ${T_{\rm{e}}}$ 为电子温度（单位eV）； ${n_{\rm{e}}}\left( x \right)$ 为鞘层区域电子密度。

将式（1）、式（4）和式（5）代入泊松方程，可得

$\dfrac{{{{\rm{d}}^2}{\mathit{\Phi}} \left( x \right)}}{{{\rm{d}}{x^2}}} = \dfrac{e}{{{\varepsilon _0}}}\left[ {{n_{\rm{e}}}\left( x \right) - \displaystyle\sum\limits_{m = 1}^N {\left( {\dfrac{{{q_m}}}{e}{n_m}\left( x \right)} \right)} } \right] = \displaystyle\sum\limits_{m = 1}^N {\dfrac{{{q_m}{n_{{\rm{s}}m}}}}{{{\varepsilon _0}}}\left[ {\exp \left( {\dfrac{{{\mathit{\Phi}} \left( x \right)}}{{{T_{\rm{e}}}}}} \right) - {{\left( {1 - \dfrac{{{\mathit{\Phi}} \left( x \right)}}{{{\varepsilon _{{\rm{s}}m}}}}} \right)}^{ - 1/2}}} \right]}$

(6)

式中： ${\varepsilon _0}$ 为真空介电常数； ${\varepsilon _{{\rm{s}}m}} = {{{M_m}u_{{\rm{s}}m}^2} \mathord{\left/ {\vphantom {{{M_m}u_{{\rm{s}}m}^2} {\left( {2{q_m}} \right)}}} \right. } {\left( {2{q_m}} \right)}}$ 为第m种离子入鞘动能。式（6）两边乘以 ${{{\rm{d}}{\mathit{\Phi}} } \mathord{\left/ {\vphantom {{d{\mathit{\Phi}} } {{\rm{d}}x}}} \right. } {{\rm{d}}x}}$ 对 $x$ 积分，可得

$\displaystyle\int_0^{\mathit{\Phi}} {\dfrac{{{\rm{d}}{\mathit{\Phi}} }}{{{\rm{d}}x}}\dfrac{{\rm{d}}}{{{\rm{d}}x}}\left( {\dfrac{{{\rm{d}}{\mathit{\Phi}} }}{{{\rm{d}}x}}} \right){\rm{d}}x} = \displaystyle\sum\limits_{m = 1}^N {\dfrac{{{q_m}{n_{{\rm{s}}m}}}}{{{\varepsilon _0}}}\displaystyle\int_0^{\mathit{\Phi}} {\dfrac{{{\rm{d}}{\mathit{\Phi}} }}{{{\rm{d}}x}}\left[ {\exp \left( {\dfrac{{\mathit{\Phi}} }{{{T_{\rm{e}}}}}} \right) - {{\left( {1 - \dfrac{{\mathit{\Phi}} }{{{\varepsilon _{{\rm{s}}m}}}}} \right)}^{ - 1/2}}} \right]{\rm{d}}x} }$

(7)

式（7）中消掉 ${\rm{d}}x$ ，并对 ${\mathit{\Phi}}$ 求积分，可得

$\dfrac{1}{2}{\left( {\dfrac{{{\rm{d}}{\mathit{\Phi}} }}{{{\rm{d}}x}}} \right)^2} = \displaystyle\sum\limits_{m = 1}^N {\dfrac{{{q_m}{n_{{\rm{s}}m}}}}{{{\varepsilon _0}}}\left[ {{T_{\rm{e}}}\exp \left( {\dfrac{{\mathit{\Phi}} }{{{T_{\rm{e}}}}}} \right) - {T_{\rm{e}}} + 2{\varepsilon _{{\rm{s}}m}}{{\left( {1 - \dfrac{{\mathit{\Phi}} }{{{\varepsilon _{{\rm{s}}m}}}}} \right)}^{1/2}} - 2{\varepsilon _{{\rm{s}}m}}} \right]}$

(8)

式（8）右端项用Taylor级数展开并保留至二阶项后，可得

$\displaystyle\sum\limits_{m = 1}^N {\dfrac{{{q_m}{n_{{\rm{s}}m}}}}{{{\varepsilon _0}}}\left[ {\dfrac{{{{\mathit{\Phi}} ^2}}}{{2{T_{\rm{e}}}}} - \dfrac{{{{\mathit{\Phi}} ^2}}}{{4{\varepsilon _{{\rm{s}}m}}}}} \right]} \geqslant 0$

(9)

式（9）成立的充分非必要条件是

$\begin{array}{*{20}{c}} {\dfrac{{{{\mathit{\Phi}} ^2}}}{2{{T_{\rm{e}}}}} - \dfrac{{{{\mathit{\Phi}} ^2}}}{{4{\varepsilon _{{\rm{s}}m}}}} \geqslant 0}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(10)

由式（10）可得

$\begin{array}{*{20}{c}} {{u_{{\rm{s}}m}} \geqslant {u_{{\rm{B}}m}} = \sqrt {{{{q_m}{T_{\rm{e}}}} \mathord{\left/ {\vphantom {{{q_m}{T_{\rm{e}}}} {{M_m}}}} \right. } {{M_m}}}} }&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(11)

式中： ${u_{{\rm{B}}m}}$ 为第m种离子玻姆速度。式（11）表明，离子到达中性区与鞘层边界面的入鞘速度不小于玻姆速度。

1.2 多组分等离子体高压查尔特鞘层的理论解

假设中性区与鞘层交界面处的总离子密度为 ${n_{{\rm{si}}}}$ ，各组分比例分别为 ${r_1}$ ， ${r_2}$ ，…， ${r_N}$ ，满足

$\left\{ \begin{gathered} \begin{array}{*{20}{c}} {{n_{{\rm{s}}m}} = {n_{{\rm{si}}}}{r_m}}&{\left( {m = 1,2, \cdots ,N} \right)} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\displaystyle\sum\limits_{m = 1}^N {{r_m}} = 1,}&{\displaystyle\sum\limits_{m = 1}^N {{n_{{\rm{s}}m}}} = {n_{{\rm{si}}}}} \end{array} \hfill \\ \end{gathered} \right.$

(12)

当离子初始能量远小于鞘层电压对应势能时，对于第m种离子的能量守恒和流连续方程可表示为

$\left\{ \begin{array}{l} {\dfrac{1}{2}{M_m}u_m^2\left( x \right) = - {q_m}{\mathit{\Phi}} \left( x \right)}\\ {{q_m}{n_m}\left( x \right){u_m}\left( x \right) = {J_m} = {q_m}{n_{{\rm{s}}m}}{u_{{\rm{s}}m}} = {q_m}{n_{{\rm{si}}}}{r_m}{u_{{\rm{s}}m}}} \end{array} \right. {\left( {m = 1,\;2,\; \cdots ,\;N} \right)}$

(13)

式中： ${u_m}\left( x \right)$ 为鞘层区域第m种离子的速度； ${\mathit{\Phi}} \left( x \right)$ 为鞘层区域电位分布。鞘层区域 $x \geqslant 0$ ， ${\mathit{\Phi}} \left( x \right) \leqslant 0$ 。

由式（13）可以推导出

$\begin{array}{*{20}{c}} {{n_m}\left( x \right) = \dfrac{{{J_m}}}{{{q_m}}}{{\left[ { - \dfrac{{2{q_m}{\mathit{\Phi}} \left( x \right)}}{{{M_m}}}} \right]}^{ - 1/2}}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(14)

式中： ${J_m}$ 代表鞘层区域内第m种离子的电流密度。各组分离子在鞘层区域不同位置的电流密度不变。

将式（14）代入泊松方程，可得

$\dfrac{{{{\rm{d}}^2}{\mathit{\Phi}} }}{{{\rm{d}}{x^2}}} = - \displaystyle\sum\limits_{m = 1}^N {\dfrac{{{J_m}}}{{{\varepsilon _0}}}{{\left( { - \dfrac{{2{q_m}{\mathit{\Phi}} }}{{{M_m}}}} \right)}^{ - 1/2}}}$

(15)

将式（15）乘以 ${{{\rm{d}}{\mathit{\Phi}} } \mathord{\left/{\vphantom {{{\rm{d}}{\mathit{\Phi}} } {dx}}} \right.} {{\rm{d}}x}}$ 并对其从0到x积分，可得

$\dfrac{1}{2}{\left( {\dfrac{{{\rm{d}}{\mathit{\Phi}} }}{{{\rm{d}}x}}} \right)^2} = \dfrac{2}{{{\varepsilon _0}}}\left[ {\displaystyle\sum\limits_{m = 1}^N {{J_m}{{\left( {\dfrac{{2{q_m}}}{{{M_m}}}} \right)}^{ - 1/2}}} } \right]{\left( { - {\mathit{\Phi}} } \right)^{1/2}}$

(16)

利用中性区与鞘层交界（ $x = 0$ 处），近似满足 ${\mathit{\Phi}} = 0$ 且 ${{{\rm{d}}{\mathit{\Phi}} } \mathord{\left/ {\vphantom {{{\rm{d}}{\mathit{\Phi}} } {{\rm{d}}x}}} \right. } {{\rm{d}}x}} = 0$ 的查尔特-朗谬尔定律边界条件，对式（16）求平方根，并取负值（ ${{{\rm{d}}{\mathit{\Phi}} } \mathord{\left/ {\vphantom {{{\rm{d}}{\mathit{\Phi}} } {{\rm{d}}x}}} \right. } {{\rm{d}}x}} < 0$ ，因鞘层区的电场为正），再次积分可得

${\left( { - {\mathit{\Phi}} } \right)^{3/4}} = \dfrac{{3x}}{2}\sqrt {\dfrac{1}{{{\varepsilon _0}}}\displaystyle\sum\limits_{m = 1}^N {\left( {{J_m}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)} }$

(17)

式（17）两端平方可得

$\dfrac{4}{9}{\varepsilon _0}\dfrac{{{{\left( { - {\mathit{\Phi}} } \right)}^{3/2}}}}{{{x^2}}} = \displaystyle\sum\limits_{m = 1}^N {\left( {{J_m}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)}$

(18)

$\begin{array}{*{20}{c}} {{J_m} = {q_m}{n_{{\rm{s}}m}}{u_{{\rm{s}}m}} = {q_m}{n_{{\rm{si}}}}{r_m}{u_{{\rm{s}}m}}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(19)

将靶面（金属壁面）处（ $x = S$ ）的电位 ${\mathit{\Phi}} = - {V_0}$ 代入式（18），可得

$\dfrac{4}{9}{\varepsilon _0}\dfrac{{{{\left( {{V_0}} \right)}^{3/2}}}}{{{S^2}}} = \displaystyle\sum\limits_{m = 1}^N {\left( {{J_m}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)}$

(20)

将式（19）代入式（20），可得

${n_{{\rm{si}}}} = \dfrac{4}{9}{\varepsilon _0}\dfrac{{V_0^{3/2}}}{{{S^2}}}{\left[ {\displaystyle\sum\limits_{m = 1}^N {\left( {{q_m}{r_m}{u_{{\rm{s}}m}}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)} } \right]^{ - 1}}$

(21)

由式（21）可得鞘层厚度表达式

$S = \dfrac{2}{3}\sqrt {{\varepsilon _0}\dfrac{{V_0^{3/2}}}{{{n_{{\rm{si}}}}}}{{\left[ {\displaystyle\sum\limits_{m = 1}^N {\left( {{q_m}{r_m}{u_{{\rm{s}}m}}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)} } \right]}^{ - 1}}}$

(22)

将式（21）代入式（19），可得

${J_m} = \dfrac{4}{9}{\varepsilon _0}\dfrac{{V_0^{3/2}}}{{{S^2}}}\dfrac{{{q_m}{r_m}{u_{{\rm{s}}m}}}}{{\displaystyle\sum\limits_{m = 1}^N {\left( {{q_m}{r_m}{u_{{\rm{s}}m}}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)} }}$

(23)

由查尔特-朗缪尔定律可知：阴极电子发射的空间限制流仅与电压、间距以及电子质量和电量相关。由式（23）给出的多组分离子高压鞘层空间限制流关系可知：多组分离子高压鞘层中每个组分的离子空间限制流除了与电压、鞘层厚度、其自身质量、电量相关，还与其初始速度、组分比例相关，另外还与其他组分离子的质量、电量、初始速度、组分比例关系密切相关。而鞘层厚度也并非是固定的，由式（22）可知：鞘层厚度是由鞘层电压、等离子体密度、各组分离子的质量、电量、初始速度、组分比例关系共同决定的。

将式（23）代入式（18），可得电势表达式，由 $E = - {{{\rm{d}}{\mathit{\Phi}} } \mathord{\left/ {\vphantom {{{\rm{d}}{\mathit{\Phi}} } {{\rm{d}}x}}} \right. } {{\rm{d}}x}}$ ，可得场强表达式为

${\mathit{\Phi}} = - {V_0}{\left( {\dfrac{x}{S}} \right)^{4/3}}$

(24)

$E = \dfrac{4}{3}\dfrac{{{V_0}}}{S}{\left( {\dfrac{x}{S}} \right)^{1/3}}$

(25)

由式（25）可知：鞘层区域场强幅值达到最大值位于靶面处。靶面处场强的表达式为

${E_{\max }} = \dfrac{4}{3}\dfrac{{{V_0}}}{S} = \dfrac{{2{V_0}}}{{\sqrt {{\varepsilon _0}\dfrac{{V_0^{3/2}}}{{{n_{{\rm{si}}}}}}{{\left[ {\displaystyle\sum\limits_{m = 1}^N {\left( {{q_m}{r_m}{u_{{\rm{s}}m}}\sqrt {\dfrac{{{M_m}}}{{2{q_m}}}} } \right)} } \right]}^{ - 1}}} }}$

(26)

对于鞘层区域中的第m种离子，由能量守恒关系式可得

$\begin{array}{*{20}{c}} {\dfrac{1}{2}{M_m}u_m^2\left( x \right) = \dfrac{1}{2}{M_m}u_{{\rm{s}}m}^2 - {q_m}{\mathit{\Phi}} \left( x \right)}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(27)

由连续性方程可得

$\begin{array}{*{20}{c}} {{n_m}\left( x \right){u_m}\left( x \right) = {n_{{\rm{s}}m}}{u_{{\rm{s}}m}}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(28)

由式（27）、式（28）可得

$\begin{array}{*{20}{c}} {{n_m}\left( x \right) = {n_{{\rm{s}}m}}{{\left[ {1 - \dfrac{{2{q_m}{\mathit{\Phi}} \left( x \right)}}{{{M_m}u_{{\rm{s}}m}^2}}} \right]}^{ - 1/2}}}&{\left( {m = 1,\;2, \; \cdots ,\;N} \right)} \end{array}$

(29)

将式（24）代入式（29），可得鞘层内第m种离子的密度分布关系式

$\begin{array}{*{20}{c}} {{n_m}\left( x \right) = \dfrac{{{n_{{\rm{s}}m}}}}{{\sqrt {1 + \dfrac{{2{q_m}{V_0}{{\left( {x/S} \right)}^{4/3}}}}{{{M_m}u_{{\rm{s}}m}^2}}} }} = \dfrac{{{n_{{\rm{si}}}}{r_m}}}{{\sqrt {1 + \dfrac{{2{q_m}{V_0}{{\left( {x/S} \right)}^{4/3}}}}{{{M_m}u_{{\rm{s}}m}^2}}} }}}&{\left( {m = 1,\;2,\; \cdots ,\;N} \right)} \end{array}$

(30)

2. 氘钛等离子体高压查尔特鞘层特性的计算与分析

氘钛合金电极储氢量高，常用作真空弧离子源的阴极材料，放电时除了会产生D离子还会产生Ti离子，从而形成氘钛混合等离子体^[14]。利用混合多组分等离子体高压查尔特鞘层动力学建模所获得的解析结果，对真空弧离子源放电产生的D⁺离子与Ti²⁺离子混合等离子体高压查尔特鞘层特性进行数值计算，分析其影响因素和行为规律。由于真空弧离子源由一系列连续的非稳态阴极斑产生，强大的内外压差导致产生的离子具有典型的超声速喷射行为，根据文献[15]的实验测试数据，D⁺离子和Ti²⁺离子的漂移能量分别为8.4，36.5 eV，换算后D⁺离子漂移速度大约为28 km/s，Ti²⁺离子漂移速度约为12.1 km/s。

等离子体参数和电参数对混合多组分等离子体高压查尔特鞘层特性的影响较为复杂，因此采用控制变量法开展多种因素（包括等离子体密度、组分比例、离子入鞘速度、引出电压等）影响下的鞘层特性（鞘层厚度、靶面场强）规律研究，最终获得离子引出稳定工作区分布范围的快速评估。

高压查尔特鞘层特性研究过程中，主要关心鞘层厚度和靶面场强2个物理量，鞘层厚度会影响引出离子的传输状态，靶面场强则对器件是否击穿的评估有重要作用。一般来说，增加鞘层厚度有利于引出离子汇聚传输，减小靶面场强则有利于避免器件内部击穿的发生。

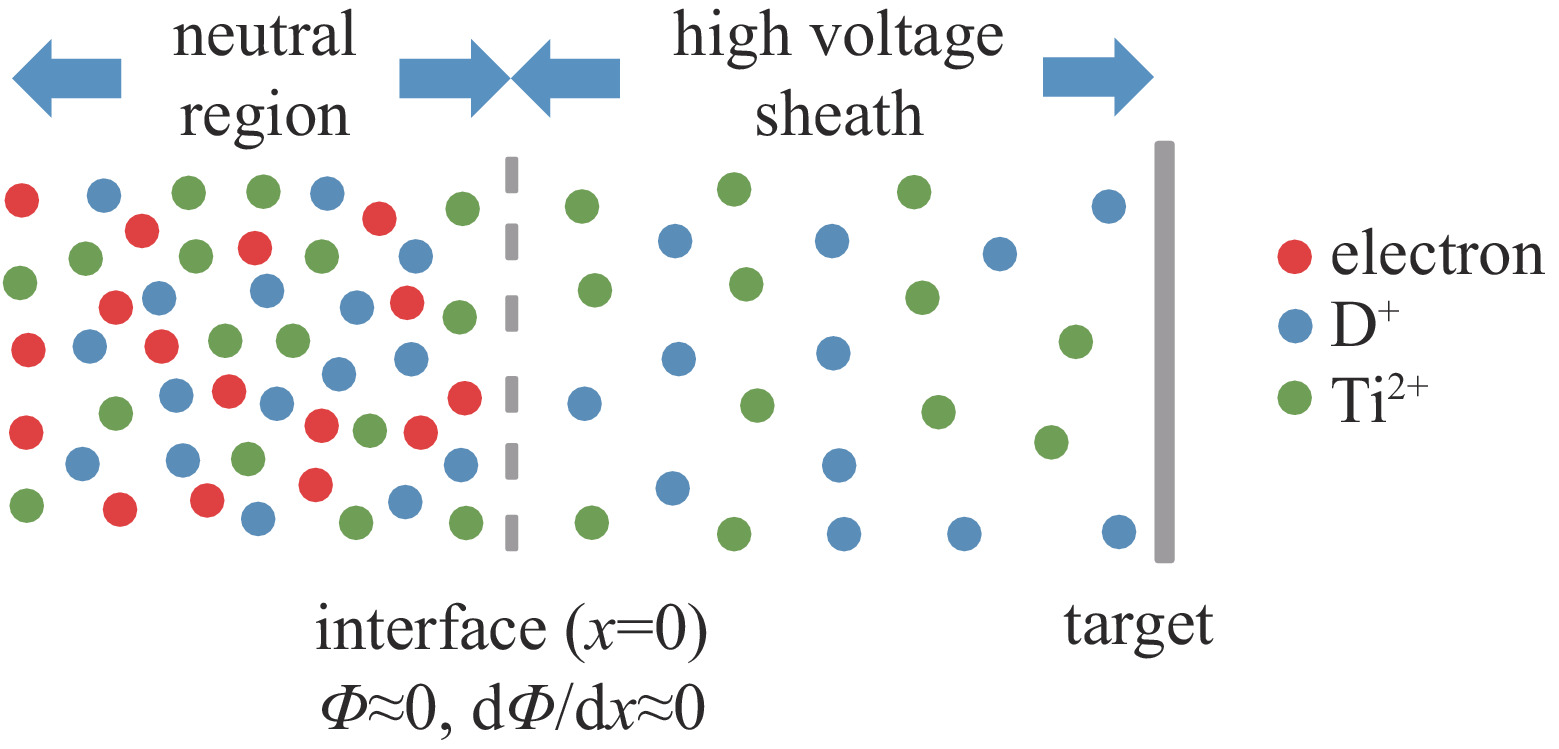
为了便于理解，图1给出了氘钛等离子体中性区和高压鞘层区示意图。这里关注和研究的是高压鞘层区域。数值计算中，设定第一类离子为D⁺离子，第二类离子为Ti²⁺离子，等离子体组分比例分别为 ${r_1}$ 和 ${r_2}$ ， ${r_2} = 1 - {r_1}$ ，D⁺和Ti²⁺离子的入鞘速度分别为 ${u_{{\rm{s}}1}}$ 和 ${u_{{\rm{s}}2}}$ ，鞘层电压为 ${V_0}$ ，鞘层边界面等离子体密度为 ${n_{{\rm{si}}}}$ 。

图 1 氘钛等离子体中性区域和高压鞘层区域示意图

Figure 1. Schematic of neutral region and high voltage sheath of mixed D⁺ and Ti²⁺ plasmas

下载: 全尺寸图片幻灯片

2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响

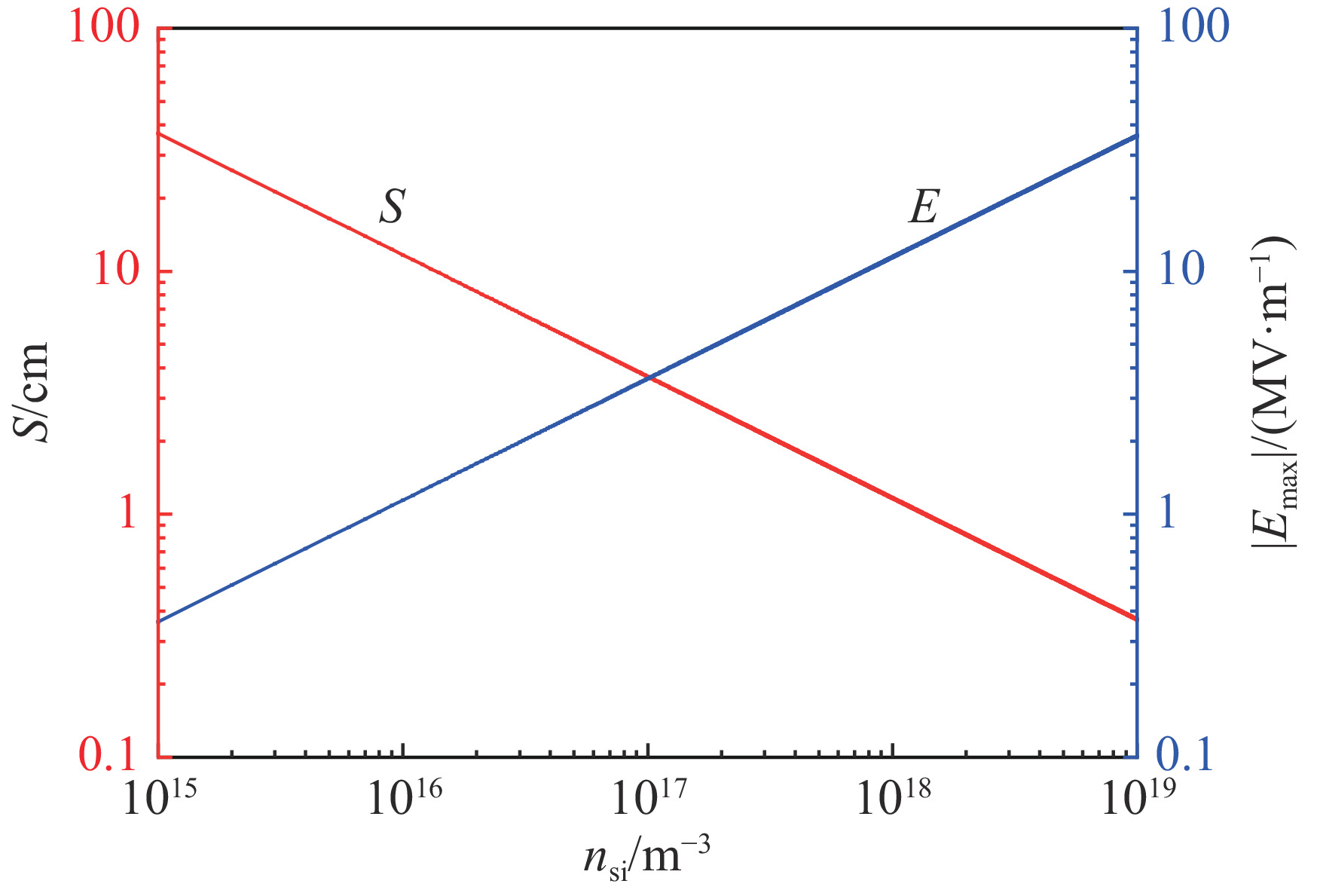
首先，设定 ${V_0} = 100\;{\rm{kV}}$ ， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论鞘层边界面等离子体密度（取值范围 ${n_{{\rm{si}}}} = {10^{15}}\sim {10^{19}}\;{{\rm{m}}^{ - 3}}$ ）与鞘层厚度 $S$ 及靶面场强 ${E_{\max}}$ 的关系。相关参数代入式（22）和式（26），可获得如图2所示的计算结果。由图2可以看出，鞘层厚度随等离子体密度的增加而减小，靶面场强随等离子体密度的增加而增加。由此可知，增加离子源等离子体密度将会导致高压鞘层厚度减小，容易造成束流发散。除此之外，增加离子源等离子体密度还会导致靶面场强增加，增大器件内部击穿风险。

图 2 鞘层厚度及靶面场强随等离子密度变化关系

Figure 2. Sheath depth and electric-field strength as a function of ion density

下载: 全尺寸图片幻灯片

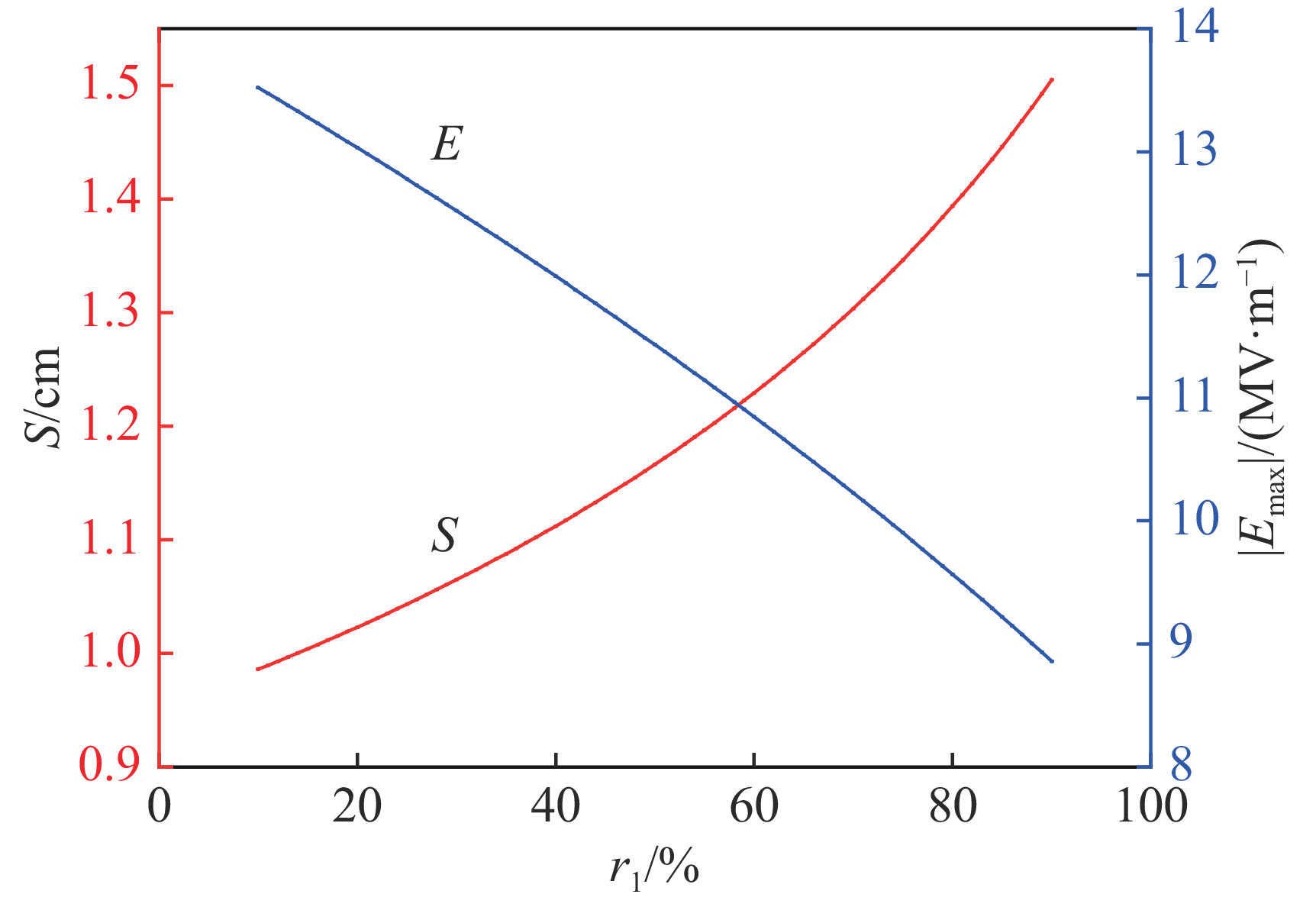
其次，设定 ${V_0} = 100\;{\rm{kV}}$ ， ${n_{{\rm{si}}}} = {10^{18}}\;{{\rm{m}}^{ - 3}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论等离子体组分比例 ${r_1}$ 和 ${r_2}$ 与鞘层厚度 $S$ 以及靶面场强 ${E_{\max}}$ 的关系。相关参数代入式（22）和式（26），可获得如图3所示的计算结果。由图3可以看出，鞘层厚度随D⁺离子比例增加而增加，靶面场强随D⁺离子比例增加而减小。由此可知，提升D⁺离子比例有利于束流的汇聚以及降低器件内部击穿风险。

图 3 鞘层厚度及靶面场强随D⁺离子占比变化关系

Figure 3. Sheath depth and electric-field strength as a function of D⁺ proportion

下载: 全尺寸图片幻灯片

2.2 各组分离子入鞘速度对鞘层特性的影响

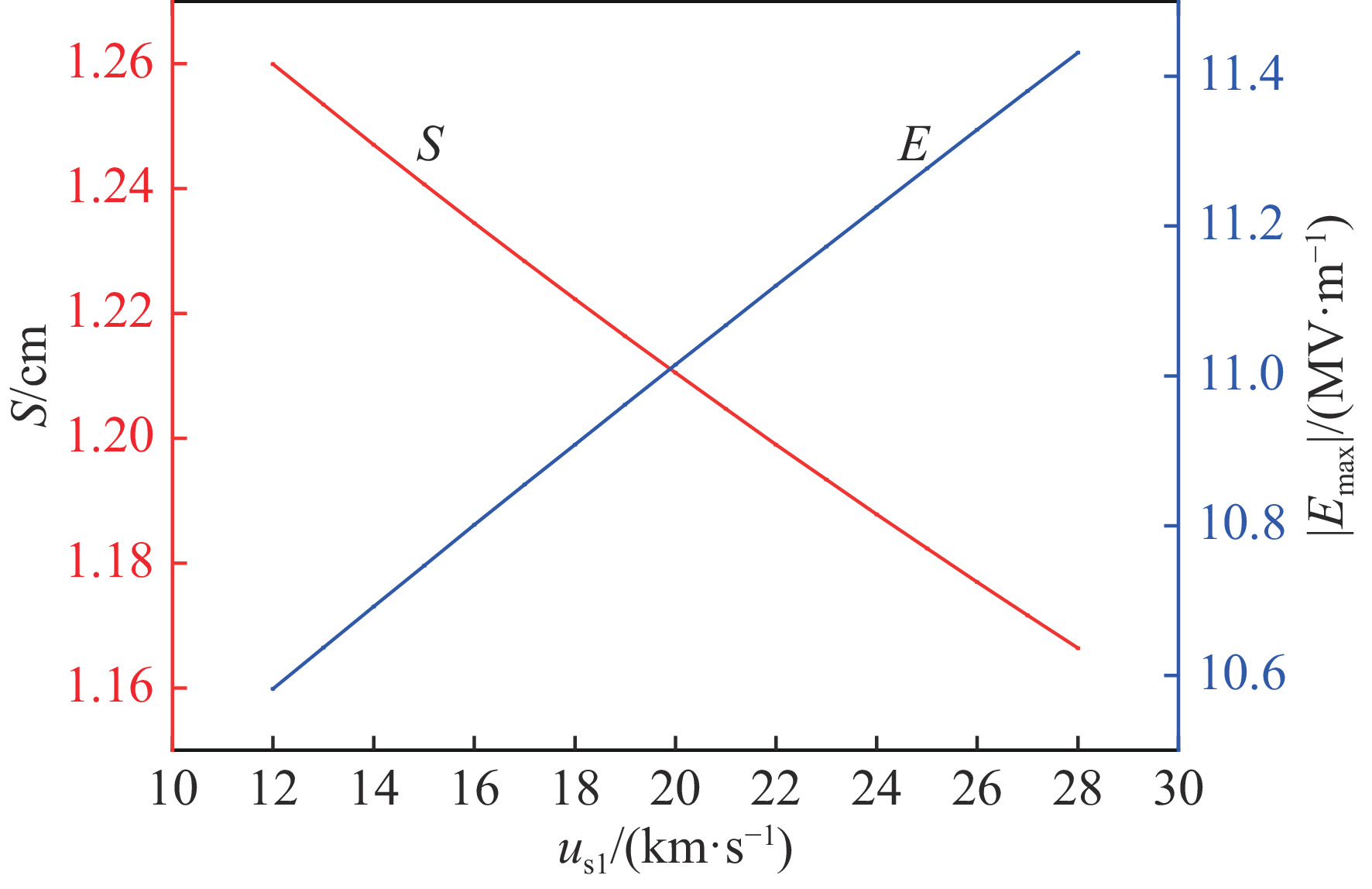
首先，设定 ${V_0} = 100\;{\rm{kV}}$ ， ${n_{{\rm{si}}}} = {10^{18}}\;{{\rm{m}}^{ - 3}}$ ， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论D⁺离子的入鞘速度 ${u_{{\rm{s}}1}}$ （范围取 $1.198 \times {10^4}\sim 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，其中 $1.198 \times {10^4}\;{\rm{m}}/{\rm{s}}$ 为D⁺离子的玻姆速度）与鞘层厚度 $S$ 以及靶面场强 ${E_{\max}}$ 的关系。相关参数代入式（22）和式（26），可获得如图4所示的计算结果。由图4可以看出，鞘层厚度随D⁺离子入鞘速度增加而减小，靶面场强随D⁺离子入鞘速度增加而增加。由此可知，降低D⁺离子入鞘速度有利于束流汇聚及降低器件内部击穿风险。

图 4 鞘层厚度及靶面场强随D⁺入鞘速度变化关系

Figure 4. Sheath depth and electric-field strength vs sheath-entering velocity of D⁺

下载: 全尺寸图片幻灯片

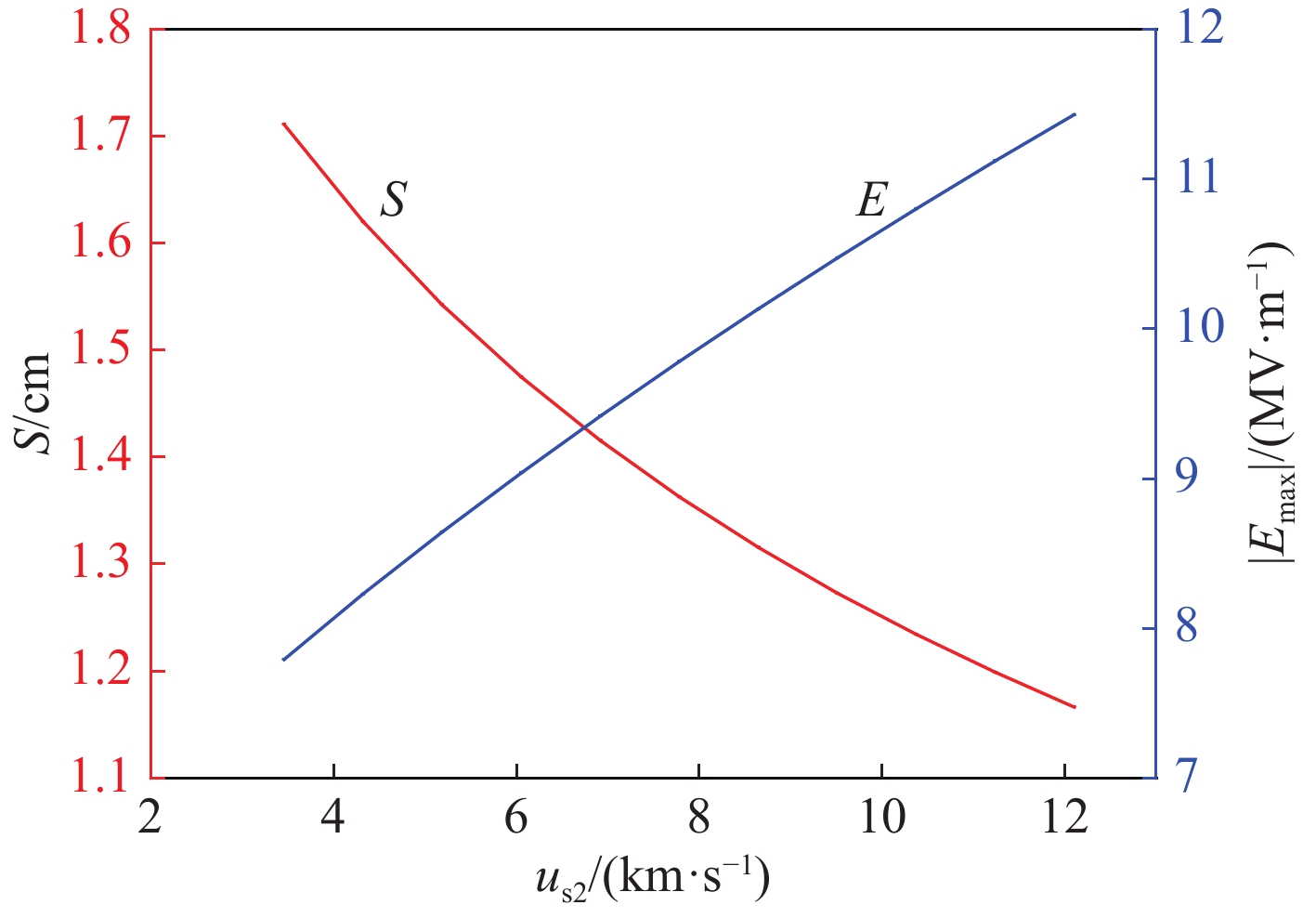
其次，设定 ${V_0} = 100\;{\rm{kV}}$ ， ${n_{{\rm{si}}}} = {10^{18}}\;{{\rm{m}}^{ - 3}}$ ， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论Ti²⁺离子的入鞘速度 ${u_{{\rm{s}}2}}$ （范围取 $3.458 \times {10^3}\sim 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，其中 $3.458 \times {10^3}\;{\rm{m}}/{\rm{s}}$ 为Ti²⁺离子的玻姆速度）与鞘层厚度 $S$ 以及靶面场强 ${E_{\max}}$ 的关系。相关参数代入式（22）和式（26），可获得如图5所示的计算结果。由图5可以看出，鞘层厚度随Ti²⁺离子入鞘速度增加而减小，靶面场强随Ti²⁺离子入鞘速度增加而增加。由此可知，降低Ti²⁺离子入鞘速度有利于束流汇聚及降低器件内部击穿风险。

图 5 鞘层厚度及靶面场强随Ti²⁺入鞘速度变化关系

Figure 5. Sheath depth and electric-field strength vs sheath-entering velocity of Ti²⁺

下载: 全尺寸图片幻灯片

2.3 电压对鞘层特性的影响

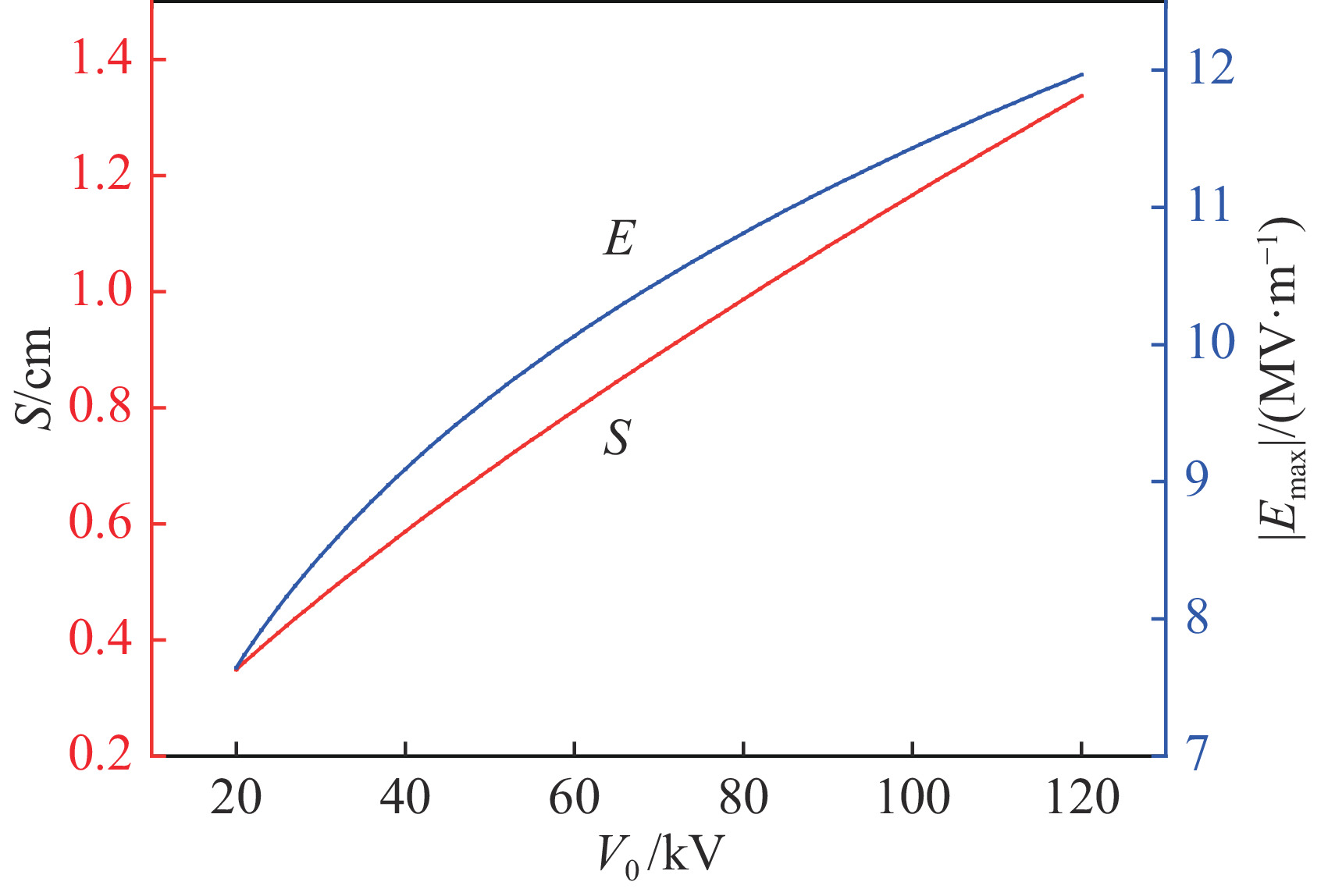
设定 ${n_{{\rm{si}}}} = {10^{18}}\;{{\rm{m}}^{ - 3}}$ ， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论电压 ${V_0}$ （范围取 $20\sim 120\;{\rm{kV}}$ ）与鞘层厚度 $S$ 以及靶面场强 ${E_{\max}}$ 的关系。相关参数代入式（22）和式（26），可获得如图6所示的计算结果。由图6可以看出，鞘层厚度随加速电压增加而增加，靶面场强随加速电压增加而增加。由此可知，增加加速电压虽然有利于束流汇聚，但会增加器件内部击穿风险。

图 6 鞘层厚度及靶面场强随加速电压变化关系

Figure 6. Sheath depth and electric-field strength as a function of accelerating voltage

下载: 全尺寸图片幻灯片

2.4 电压对各组分电流密度和总电流密度的影响

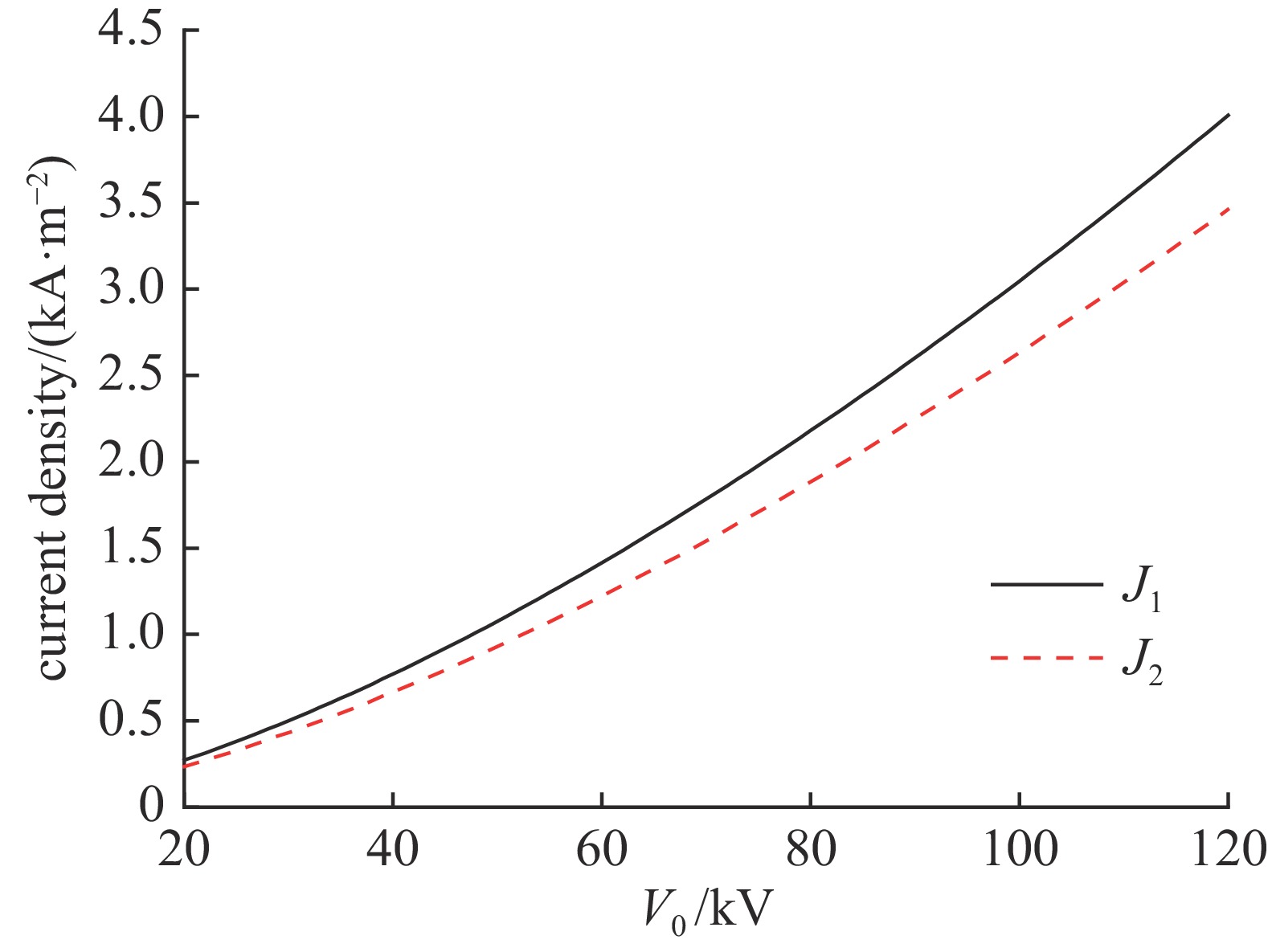
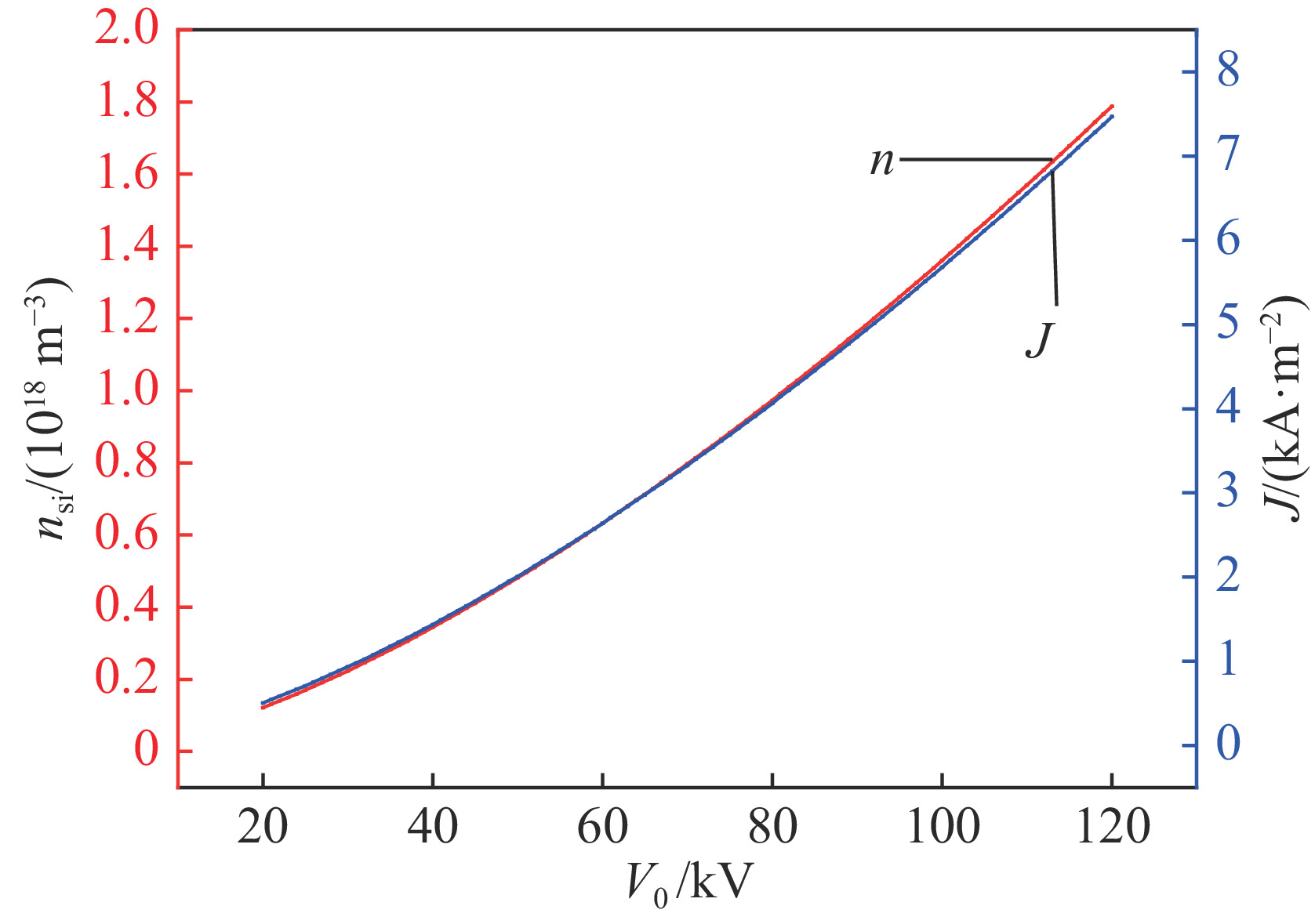
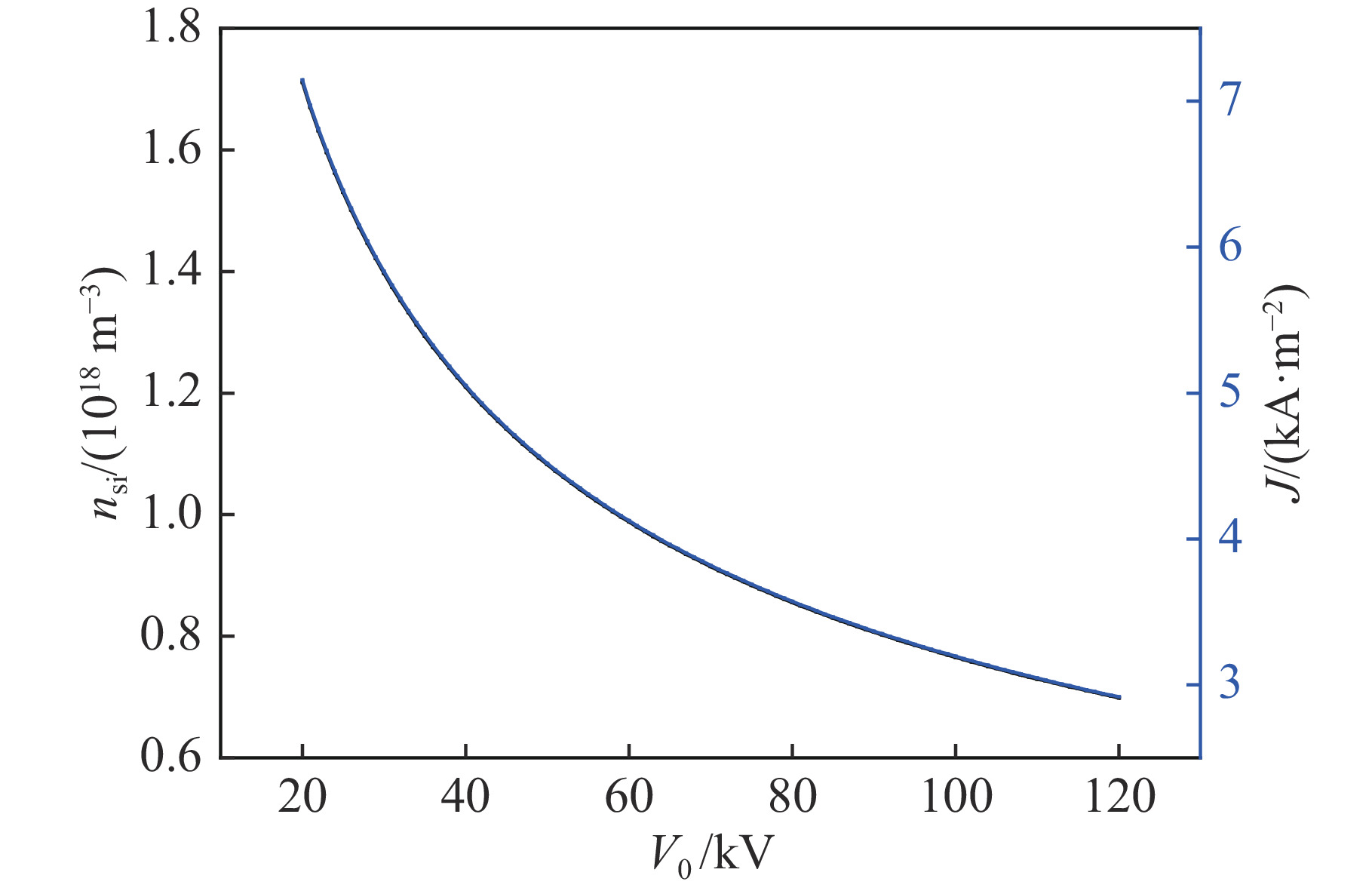
首先，设定鞘层厚度 $S = 0.01\;{\rm{m}}$ 保持不变， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论电压 ${V_0}$ （范围取 $20\sim 120\;{\rm{kV}}$ ）与鞘层交界面等离子体密度 ${n_{{\rm{si}}}}$ 、总电流密度 $J$ 以及D⁺离子电流密度 ${J_1}$ 和Ti²⁺离子电流密度 ${J_2}$ 的关系。相关参数代入式（21）和式（23），可获得如图7和图8所示的计算结果。由图7、图8可以看出，保持鞘层厚度不变情况下，D⁺离子和Ti²⁺离子电流密度均随加速电压增加而增加，D⁺离子电流密度随加速电压增幅度大于Ti²⁺离子电流密度增加幅度。保持鞘层厚度不变情况下，鞘层交界面等离子体密度及总电流密度均随加速电压增加而增加。

图 7 组分电流密度随电压变化关系（保持鞘层厚度不变）

Figure 7. Current density components vs voltage (fixed sheath depth)

下载: 全尺寸图片幻灯片

图 8 等离子体密度和总电流密度随电压变化关系（保持鞘层厚度不变）

Figure 8. Total current density and interface plasma density vs voltage (fixed sheath depth)

下载: 全尺寸图片幻灯片

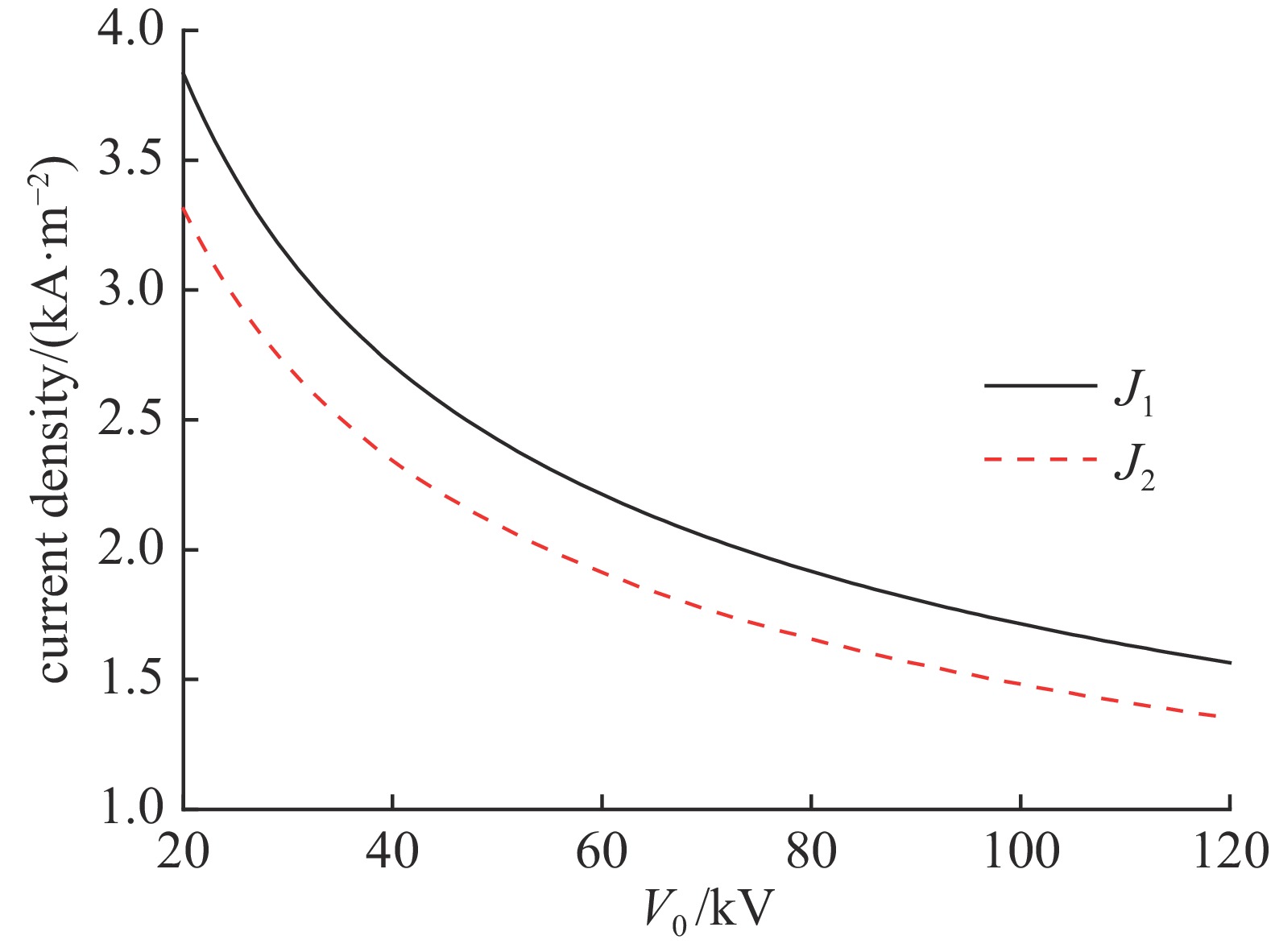
其次，设定靶面场强 ${E_{\max }} = 10\;{\rm{MV}}/{\rm{m}}$ 保持不变， ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，讨论电压 ${V_0}$ （范围取 $20\sim 120\;{\rm{kV}}$ ）与鞘层交界面等离子体密度 ${n_{{\rm{s}}i}}$ 、总电流密度 $J$ 以及D⁺离子电流密度 ${J_1}$ 和Ti²⁺离子电流密度 ${J_2}$ 的关系。相关参数代入式（21）、式（23）和式（26），可获得如图9和图10所示的计算结果。由图9、图10可以看出，保持靶面场强幅值不变情况下，D⁺离子和Ti²⁺离子电流密度均随加速电压增加而减小。保持靶面场强幅值不变情况下，鞘层交界面等离子体密度及总电流密度均随加速电压增加而降低。

图 9 组分电流密度随加速电压变化关系（保持靶面场强不变）

Figure 9. Current density components vs voltage (fixed E_max)

下载: 全尺寸图片幻灯片

图 10 等离子体密度及总电流密度随加速电压变化关系（保持靶面场强不变）

Figure 10. Total current density and interface plasma density vs voltage (fixed E_max)

下载: 全尺寸图片幻灯片

2.5 多组分混合离子引出稳定工作区域的选取

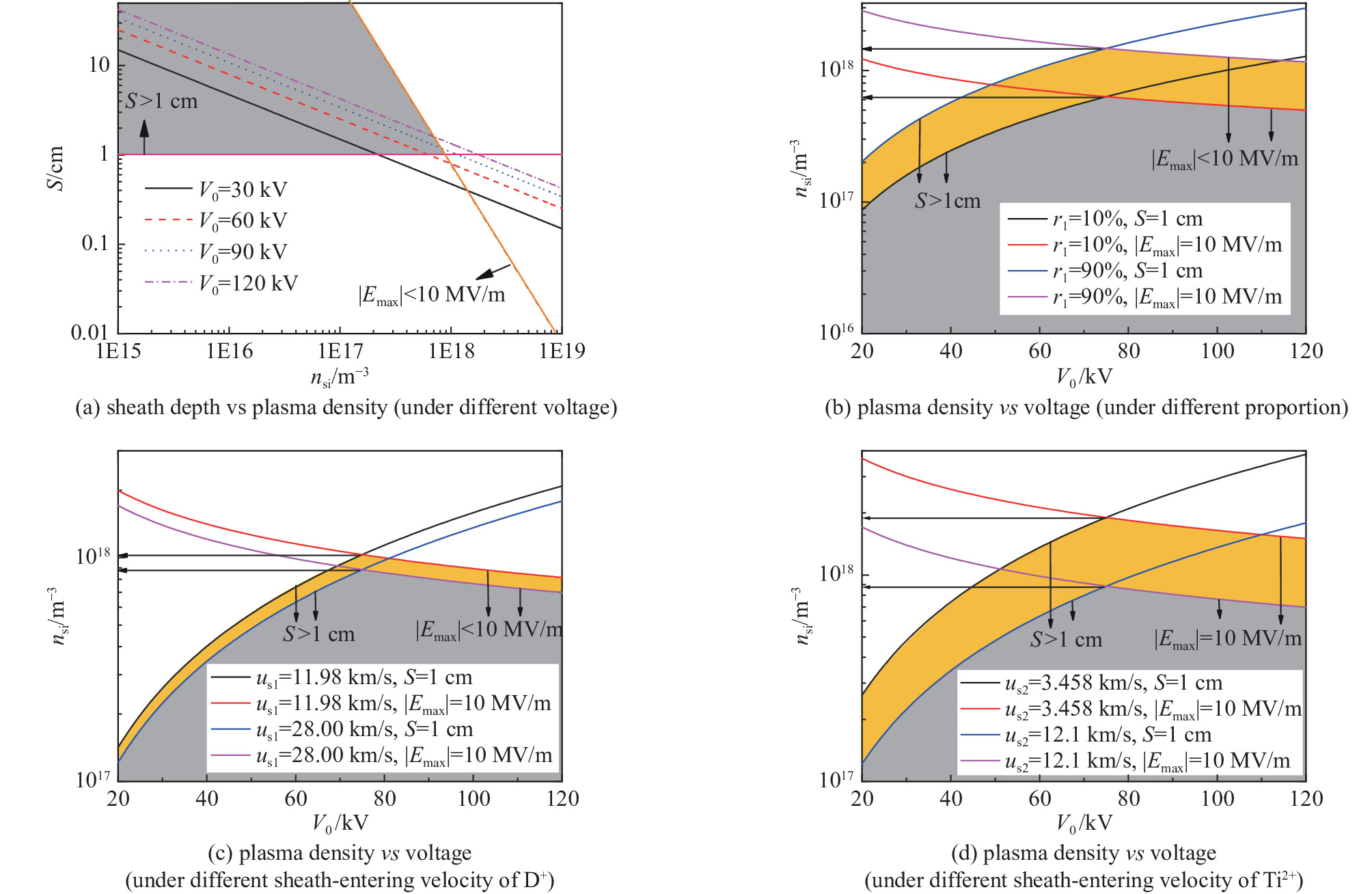
设定 ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，图11（a）给出了不同电压（ ${V_0}$ 范围取 $30\sim 120\;{\rm{kV}}$ ）情况下鞘层交界面等离子体密度与鞘层厚度的关系。图11（a）中粉红色实线为鞘层厚度 $S = 1\;{\rm{cm}}$ 的分界线，相关数据表明 $S < 1\;{\rm{cm}}$ 束流多呈发散趋势，而 $S > 1\;{\rm{cm}}$ 束流多呈汇聚特性。图11中黄色实线代表靶面场强幅值 $\left| {{E_{\max }}} \right| = 10\;{\rm{MV}}/{\rm{m}}$ 的分界线，相关数据表明 $\left| {{E_{\max }}} \right| > 10\;{\rm{MV}}/{\rm{m}}$ 器件易发生击穿。因此，离子引出稳定工作区域应满足： $S > 1\;{\rm{cm}}$ 且 $\left| {{E_{\max }}} \right| < 10\;{\rm{MV}}/{\rm{m}}$ 。其含义是：既要防止鞘层发生击穿，还要确保离子束流达到汇聚传输状态。图11（a）中灰色区域即为离子引出稳定工作区域，可以看出，随着加速电压的增加，离子引出稳定工作区域范围有增加趋势。等离子体密度较高或加速电压较高，容易发生击穿；等离子体密度较高或加速电压较低，容易造成束流引出发散。

图 11 多组分混合离子引出稳定工作区域图

Figure 11. Stable operating region for extraction of mixed plasmas

下载: 全尺寸图片幻灯片

设定 ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，图11（b）给出了不同组分占比（ ${r_1} = 10{\text{%}}$ ， ${r_1} = 90{\text{%}}$ ）情况下鞘层交界面等离子体密度与加速电压的关系。图11（b）中灰色区域为 ${r_1} = 10{\text{%}}$ 情况下的离子引出稳定工作区域，灰色区域加橘色区域为 ${r_1} = 90{\text{%}}$ 情况下的离子引出稳定工作区域，因此混合多组分等离子体中D⁺离子所占比例越大，混合离子引出稳定工作区域的范围更广。另外，可以更加明显地看出：随加速电压的增加，离子引出稳定工作区域范围呈现先增加后减小的趋势。

设定 ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，图11（c）给出了不同D⁺离子入鞘速度（ ${u_{{\rm{s}}1}} = 1.198 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ）情况下鞘层交界面等离子体密度与加速电压的关系。图11（c）中灰色区域为 ${u_{{\rm{s}}1}} = 2.8 \times {10^4}\;{\rm{m}}/{\rm{s}}$ 情况下的离子引出稳定工作区域，灰色区域加橘色区域为 ${u_{{\rm{s}}1}} = 1.198 \times {10^4}\;{\rm{m}}/{\rm{s}}$ 情况下的离子引出稳定工作区域，因此混合多组分等离子体中D⁺离子入鞘速度越小，混合离子引出稳定工作区域的范围更广。另外，随加速电压的增加，离子引出稳定工作区域范围呈现先增加后减小的趋势。

设定 ${r_1} = {r_2} = 50{\text{%}}$ ， ${u_{{\rm{s}}1}} = 1.198 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ，图11（d）给出了不同Ti²⁺离子入鞘速度（ ${u_{{\rm{s}}2}} = 3.458 \times {10^3}\;{\rm{m}}/{\rm{s}}$ ， ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ ）情况下鞘层交界面等离子体密度与加速电压的关系。图11（d）中灰色区域为 ${u_{{\rm{s}}2}} = 1.21 \times {10^4}\;{\rm{m}}/{\rm{s}}$ 情况下的离子引出稳定工作区域，灰色区域加橘色区域为 ${u_{{\rm{s}}2}} = 3.458 \times {10^3}\;{\rm{m}}/{\rm{s}}$ 情况下的离子引出稳定工作区域，因此混合多组分等离子体中Ti²⁺离子入鞘速度越小，混合离子引出稳定工作区域的范围更广。另外，随加速电压的增加，离子引出稳定工作区域范围呈现先增加后减小的趋势。

3. 结　论

首先建立了混合多组分等离子体高压查尔特鞘层动力学模型，获得了多组分离子入鞘玻姆速度、鞘层厚度、鞘内电势、鞘内场强以及鞘内各组分密度分布的解析表达式。其次，应用建立的混合多组分等离子体高压查尔特鞘层动力学模型，数值研究了氘钛等离子体高压查尔特鞘层特性及其影响因素和相关规律。

动力学理论的研究结果表明，保持工作电压、离子组分比例以及入鞘速度不变情况下，增加等离子体密度将导致鞘层厚度减小以及靶面场强幅值增加，不利聚束且易击穿。保持工作电压、等离子体密度以及入鞘速度不变情况下，增加D⁺离子比例将导致鞘层厚度增加以及靶面场强幅值减小，利于聚束且防击穿。保持工作电压、等离子体密度及离子组分比例不变情况下，减小D⁺离子或Ti²⁺离子入鞘速度将导致鞘层厚度增加以及靶面场强幅值减小，利于聚束且防击穿。保持等离子体密度、离子组分比例以及入鞘速度不变情况下，鞘层厚度及靶面场强均随加速电压增加而增加，增加加速电压虽有利于聚束，但会增加击穿风险。保持鞘层厚度固定不变情况下，D⁺和Ti²⁺离子电流密度、等离子体密度以及总电流密度均随加速电压增加而增加。保持靶面场强幅值固定不变情况下，D⁺和Ti²⁺离子电流密度、等离子体密度及总电流密度均随加速电压增加而降低。保持离子组分比例和入鞘速度不变情况下，随加速电压的增加，离子引出稳定工作区域范围呈现先增加后减小的趋势。保持其他条件不变情况下，增加D⁺离子比例，或减小D⁺离子和Ti²⁺离子入鞘速度，均会显著增加混合离子引出稳定工作区域范围。

图 1 氘钛等离子体中性区域和高压鞘层区域示意图

Figure 1. Schematic of neutral region and high voltage sheath of mixed D⁺ and Ti²⁺ plasmas

下载: 全尺寸图片幻灯片

图 2 鞘层厚度及靶面场强随等离子密度变化关系

Figure 2. Sheath depth and electric-field strength as a function of ion density

下载: 全尺寸图片幻灯片

图 3 鞘层厚度及靶面场强随D⁺离子占比变化关系

Figure 3. Sheath depth and electric-field strength as a function of D⁺ proportion

下载: 全尺寸图片幻灯片

图 4 鞘层厚度及靶面场强随D⁺入鞘速度变化关系

Figure 4. Sheath depth and electric-field strength vs sheath-entering velocity of D⁺

下载: 全尺寸图片幻灯片

图 5 鞘层厚度及靶面场强随Ti²⁺入鞘速度变化关系

Figure 5. Sheath depth and electric-field strength vs sheath-entering velocity of Ti²⁺

下载: 全尺寸图片幻灯片

图 6 鞘层厚度及靶面场强随加速电压变化关系

Figure 6. Sheath depth and electric-field strength as a function of accelerating voltage

下载: 全尺寸图片幻灯片

图 7 组分电流密度随电压变化关系（保持鞘层厚度不变）

Figure 7. Current density components vs voltage (fixed sheath depth)

下载: 全尺寸图片幻灯片

图 8 等离子体密度和总电流密度随电压变化关系（保持鞘层厚度不变）

Figure 8. Total current density and interface plasma density vs voltage (fixed sheath depth)

下载: 全尺寸图片幻灯片

图 9 组分电流密度随加速电压变化关系（保持靶面场强不变）

Figure 9. Current density components vs voltage (fixed E_max)

下载: 全尺寸图片幻灯片

图 10 等离子体密度及总电流密度随加速电压变化关系（保持靶面场强不变）

Figure 10. Total current density and interface plasma density vs voltage (fixed E_max)

下载: 全尺寸图片幻灯片

图 11 多组分混合离子引出稳定工作区域图

Figure 11. Stable operating region for extraction of mixed plasmas

下载: 全尺寸图片幻灯片

参考文献(15)

[1]	Brown I G. The physics and technology of ion sources[M]. 2nd ed. Weinheim: Wiley-VCH, 2004.
[2]	Boxman R L, Goldsmith S, Greenwood A. Twenty-five years of progress in vacuum arc research and utilization[J]. IEEE Transactions on Plasma Science, 1997, 25(6): 1174-1186. doi: 10.1109/27.650894
[3]	Boxman R L, Sanders D M, Martin P J. Handbook of vacuum arc science and technology[M]. Park Ridge: Noyes Publications, 1995.
[4]	Benilov M S. Understanding and modelling plasma-electrode interaction in high-pressure arc discharges: a review[J]. Journal of Physics D: Applied Physics, 2008, 41: 144001. doi: 10.1088/0022-3727/41/14/144001
[5]	Kovaleski S D. Calculation of the ion extraction boundary of a plasma ion source[J]. IEEE Transactions on Plasma Science, 2006, 34(1): 23-27. doi: 10.1109/TPS.2005.863565
[6]	金大志, 戴晶怡, 杨中海. 等离子体离子源发射面的理论计算与数值模拟[J]. 强激光与粒子束, 2008, 20(4):679-682. (Jin Dazhi, Dai Jingyi, Yang Zhonghai. Estimation and simulation of emitting surface in plasma ion source[J]. High Power Laser and Particle Beams, 2008, 20(4): 679-682 Jin Dazhi, Dai Jingyi, Yang Zhonghai. Estimation and simulation of emitting surface in plasma ion source[J]. High Power Laser and Particle Beams, 2008, 20(4): 679-682
[7]	Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing[M]. 2nd ed. Hoboken: Wiley-Interscience, 2005.
[8]	Riemann K U. The Bohm criterion and sheath formation[J]. Journal of Physics D:Applied Physics, 1991, 24(4): 493-518. doi: 10.1088/0022-3727/24/4/001
[9]	Benilov M S. The Child-Langmuir law and analytical theory of collisionless to collision-dominated sheaths[J]. Plasma Sources Science and Technology, 2009, 18: 014005. doi: 10.1088/0963-0252/18/1/014005
[10]	Brown I G, Monteiro O R, Bilek M M M. High voltage sheath behavior in a drifting plasma[J]. Applied Physics Letters, 1999, 74(17): 2426-2428. doi: 10.1063/1.123869
[11]	Anders A. Breakdown of the high-voltage sheath in metal plasma immersion ion implantation[J]. Applied Physics Letters, 2000, 76(1): 28-30. doi: 10.1063/1.125645
[12]	Bilek M M M. Effect of sheath evolution on metal ion implantation in a vacuum arc plasma source[J]. Journal of Applied Physics, 2001, 89(2): 923-927. doi: 10.1063/1.1331072
[13]	陈磊, 金大志, 石磊, 等. 混合离子束阴极真空弧等离子体鞘层特性[J]. 强激光与粒子束, 2012, 24(8):1856-1860. (Chen Lei, Jin Dazhi, Shi Lei, et al. Sheath characteristics of vacuum arc plasma for mixed ion beam[J]. High Power Laser and Particle Beams, 2012, 24(8): 1856-1860 doi: 10.3788/HPLPB20122408.1856 Chen Lei, Jin Dazhi, Shi Lei, et al. Sheath characteristics of vacuum arc plasma for mixed ion beam[J]. High Power Laser and Particle Beams, 2012, 24(8): 1856-1860 doi: 10.3788/HPLPB20122408.1856
[14]	董攀, 李杰, 郑乐, 等. 真空弧放电TiH合金阴极表面形貌分析[J]. 强激光与粒子束, 2018, 30:014001. (Dong Pan, Li Jie, Zheng Le, et al. Surface morphology analysis of TiH cathode in vacuum arc discharge[J]. High Power Laser and Particle Beams, 2018, 30: 014001 doi: 10.11884/HPLPB201830.170356 Dong Pan, Li Jie, Zheng Le, et al. Surface morphology analysis of TiH cathode in vacuum arc discharge[J]. High Power Laser and Particle Beams, 2018, 30: 014001 doi: 10.11884/HPLPB201830.170356
[15]	Chen Lei, Jin Dazhi, Cheng Liang, et al. Ion charge state distribution and ion velocities in the titanium hydride cathodic vacuum arc plasmas[J]. Vacuum, 2012, 86(7): 813-816. doi: 10.1016/j.vacuum.2011.01.014

施引文献

资源附件(0)

访问统计

点击查看大图

图(11)

计量

文章访问数: 735
HTML全文浏览量: 247
PDF下载量: 48
被引次数: 0

1. 混合多组分等离子体高压查尔特鞘层的动力学建模
1.1 多组分离子入鞘速度的确定
1.2 多组分等离子体高压查尔特鞘层的理论解
2. 氘钛等离子体高压查尔特鞘层特性的计算与分析
2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响
2.2 各组分离子入鞘速度对鞘层特性的影响
2.3 电压对鞘层特性的影响
2.4 电压对各组分电流密度和总电流密度的影响
2.5 多组分混合离子引出稳定工作区域的选取
3. 结　论

1. 混合多组分等离子体高压查尔特鞘层的动力学建模
1.1 多组分离子入鞘速度的确定
1.2 多组分等离子体高压查尔特鞘层的理论解
2. 氘钛等离子体高压查尔特鞘层特性的计算与分析
2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响
2.2 各组分离子入鞘速度对鞘层特性的影响
2.3 电压对鞘层特性的影响
2.4 电压对各组分电流密度和总电流密度的影响
2.5 多组分混合离子引出稳定工作区域的选取
3. 结　论

参考文献(15)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

氘钛等离子体高压查尔特鞘层特性理论研究

doi: 10.11884/HPLPB202234.210457

作者简介:
沈伯昊，shenbohao20@gscaep.ac.cn

通讯作者:
董　烨，dongye0682@sina.com

计量

Theoretical study on characteristics of high voltage Child-sheath of mixed D⁺ and Ti²⁺ plasmas

1. 混合多组分等离子体高压查尔特鞘层的动力学建模

1.1 多组分离子入鞘速度的确定

1.2 多组分等离子体高压查尔特鞘层的理论解

2. 氘钛等离子体高压查尔特鞘层特性的计算与分析

2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响

2.2 各组分离子入鞘速度对鞘层特性的影响

2.3 电压对鞘层特性的影响

2.4 电压对各组分电流密度和总电流密度的影响

2.5 多组分混合离子引出稳定工作区域的选取

3. 结　论

计量

目录

1. 混合多组分等离子体高压查尔特鞘层的动力学建模

1.1 多组分离子入鞘速度的确定

1.2 多组分等离子体高压查尔特鞘层的理论解

2. 氘钛等离子体高压查尔特鞘层特性的计算与分析

2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响

2.2 各组分离子入鞘速度对鞘层特性的影响

2.3 电压对鞘层特性的影响

2.4 电压对各组分电流密度和总电流密度的影响

2.5 多组分混合离子引出稳定工作区域的选取

3. 结　论

留言板

氘钛等离子体高压查尔特鞘层特性理论研究

doi: 10.11884/HPLPB202234.210457

作者简介: 沈伯昊，shenbohao20@gscaep.ac.cn

通讯作者: 董 烨，dongye0682@sina.com

计量

出版历程

Theoretical study on characteristics of high voltage Child-sheath of mixed D+ and Ti2+ plasmas

1. 混合多组分等离子体高压查尔特鞘层的动力学建模

1.1 多组分离子入鞘速度的确定

1.2 多组分等离子体高压查尔特鞘层的理论解

2. 氘钛等离子体高压查尔特鞘层特性的计算与分析

2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响

2.2 各组分离子入鞘速度对鞘层特性的影响

2.3 电压对鞘层特性的影响

2.4 电压对各组分电流密度和总电流密度的影响

2.5 多组分混合离子引出稳定工作区域的选取

3. 结 论

计量

出版历程

目录

1. 混合多组分等离子体高压查尔特鞘层的动力学建模

1.1 多组分离子入鞘速度的确定

1.2 多组分等离子体高压查尔特鞘层的理论解

2. 氘钛等离子体高压查尔特鞘层特性的计算与分析

2.1 鞘层边界面等离子体密度及各组分离子比例关系对鞘层特性的影响

2.2 各组分离子入鞘速度对鞘层特性的影响

2.3 电压对鞘层特性的影响

2.4 电压对各组分电流密度和总电流密度的影响

2.5 多组分混合离子引出稳定工作区域的选取

3. 结 论

作者简介:
沈伯昊，shenbohao20@gscaep.ac.cn

通讯作者:
董　烨，dongye0682@sina.com

Theoretical study on characteristics of high voltage Child-sheath of mixed D⁺ and Ti²⁺ plasmas

3. 结　论

3. 结　论