95 MeV射频电子直线加速器辐射防护分析

李迪开; 曹磊峰; 池云龙; 周征; 陈秋宏; 张春晖; 代艳萌; 俞健; 颜苗苗; 邓嘉玲; 汪雪; 周沧涛

doi:10.11884/HPLPB202234.210518

95 MeV射频电子直线加速器辐射防护分析

doi: 10.11884/HPLPB202234.210518

李迪开^{1, 2,},
曹磊峰^{2, 3, ,},
池云龙⁴,
周征⁵,
陈秋宏⁶,
张春晖^{2, 3},
代艳萌^{1, 2},
俞健^{2, 3},
颜苗苗^{2, 3},
邓嘉玲^{2, 3},
汪雪^{2, 3},
周沧涛^{1, 2, 3}

1.
深圳技术大学工程物理学院，广东深圳 518118
2.
深圳技术大学深圳市超强激光与先进材料技术重点实验室，广东深圳 518118
3.
深圳技术大学先进材料测试技术研究中心，广东深圳 518118
4.
中国科学院高能物理研究所，北京 100049
5.
中国工程物理研究院应用电子学研究所，四川绵阳 621900
6.
广东中科揽胜辐射防护有限公司，广东佛山 528200

基金项目: 广东省教育厅普通高校特色创新项目(2021KTSCX113); 博士后出站留（来）深科研资助项目; 深圳技术大学新引进高端人才财政补助项目（20200206）。

详细信息

作者简介:
李迪开，lidikai@sztu.edu.cn

通讯作者:
曹磊峰，caoleifeng@sztu.edu.cn

中图分类号: TL508
计量
- 文章访问数: 979
- HTML全文浏览量: 197
- PDF下载量: 96
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-25
- 修回日期: 2022-03-16
- 网络出版日期: 2022-04-06
- 刊出日期: 2022-06-15

Radiation protection analysis of 95 MeV RF electron linac

Li Dikai^{1, 2
,},
Cao Leifeng^{2, 3
, ,},
Chi Yunlong⁴,
Zhou Zheng⁵,
Chen Qiuhong⁶,
Zhang Chunhui^{2, 3},
Dai Yanmeng^{1, 2},
Yu Jian^{2, 3},
Yan Miaomiao^{2, 3},
Deng Jialing^{2, 3},
Wang Xue^{2, 3},
Zhou Cangtao^{1, 2, 3}

1.
College of Engineering Physics, Shenzhen Technology University, Shenzhen 518118, China
2.
Shenzhen Key Laboratory of Ultraintense Laser and Advanced Material Technology, Shenzhen Technology University, Shenzhen 518118, China
3.
Center for Advanced Material Diagnostic Technology, Shenzhen Technology University, Shenzhen 518118, China
4.
Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
5.
Institute of Applied Electronics, CAEP, Mianyang 621900, China
6.
ZhongkeLansheng Radiate Protection Technology Coperation Limited, Foshan 528200, China

摘要

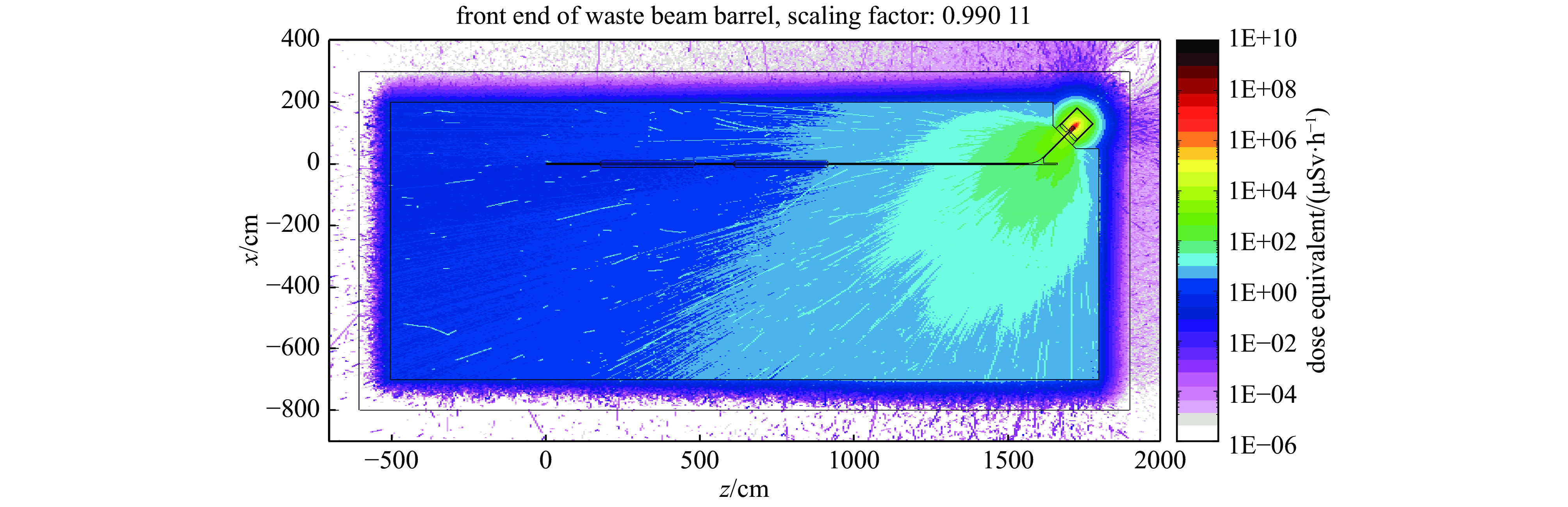
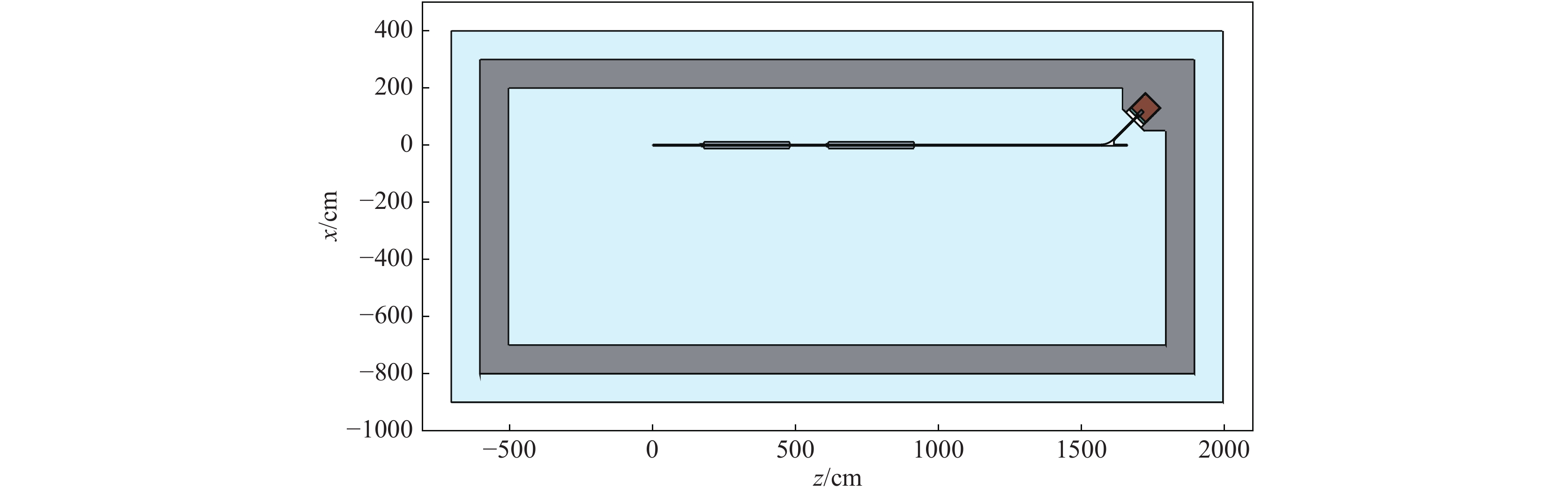
摘要: 应相关建设安评、环评、稳评以及职业健康评估的要求，电子加速器设计过程中即应对其辐射情况进行分析。针对电子能量为40～95 MeV可调的光阴极微波电子枪直线加速器，对其辐射源项进行分析，并讨论了可能的辐射防护措施的效果。采用蒙特卡罗软件FLUKA对电子束流和加速器进行建模，通过模拟计算发现，加速器产生的等效剂量分布主要位于废束桶中，废束桶以外辐射剂量迅速下降，在电子加速器实验大厅四周设置混凝土墙体的情况下辐射等效剂量率将随墙体厚度迅速下降。若混凝土墙体厚度设置为1 m，则墙体外工作人员所在区域辐射等效剂量率不高于1 μSv/h量级，能够有效屏蔽加速器产生的电离辐射，给工作人员提供有效防护。研究方法及结果对同能区同类型加速器建设中的辐射分析及辐射防护评估具有一定的参考价值。
- 电子加速器 /
- FLUKA模拟 /
- 电离辐射 /
- 辐射源项分析 /
- 辐射防护
Abstract: According to the requirements of relevant construction safety assessment, environmental assessment, stability assessment and occupational health assessment, the radiation situation of electron accelerator should be analyzed in the design process. The radiation source of photocathode RF electron gun linac with adjustable electron energy from 40 MeV to 95 MeV was analyzed, and the effect of possible radiation protection was discussed. Monte Carlo software FLUKA was used to model the electron beam and accelerator. Through simulation calculation, it is found that the dose equivalent distribution generated by the accelerator is mainly located in the beam dump, and the radiation dose outside the beam dump decreases rapidly. When the concrete shielding wall is set around the electron accelerator experimental hall, the radiation dose equivalent will decrease rapidly with the wall thickness. If the thickness of the concrete shielding wall was set to 1 m, the radiation dose equivalent in the area where the staff outside the shielding wall were located should not be higher than 1 μSv/h. So, the wall can effectively shield the ionizing radiation generated by the accelerator and provide effective protection for the staff.
- electron accelerator /
- FLUKA simulation /
- ionizing radiation /
- radiation source term analysis /
- radiation protection

HTML全文

图 1 加速器及四周防护混凝土墙体整体几何建模

Figure 1. Overall geometric modeling of accelerator and surrounding protective shielding wall

下载: 全尺寸图片幻灯片

图 2 废束桶工程设计图

Figure 2. Engineering drawing of beam dump

下载: 全尺寸图片幻灯片

图 3 束流从废束桶前开始运动产生的等效剂量分布(水平面图)

Figure 3. Dose equivalent distribution produced by the beam moving from the front of the beam dump(horizontal plane)

下载: 全尺寸图片幻灯片

图 4 束流从废束桶前开始运动产生的等效剂量分布(垂直面图)

Figure 4. Dose equivalent distribution produced by the beam moving from the front of the beam dump (vertical plane)

下载: 全尺寸图片幻灯片

图 5 束流从废束桶前开始运动产生的等效剂量在顶棚混凝土厚度0.5 m处分布(水平面图)

Figure 5. Dose equivalent distribution, at the height where the concrete thickness of the ceiling is 0.5 m, produced by the beam moving from the front of the beam dump (horizontal plane)

下载: 全尺寸图片幻灯片

表 1 各重要点位束流参数表

Table 1. Parameters of beam at important positions

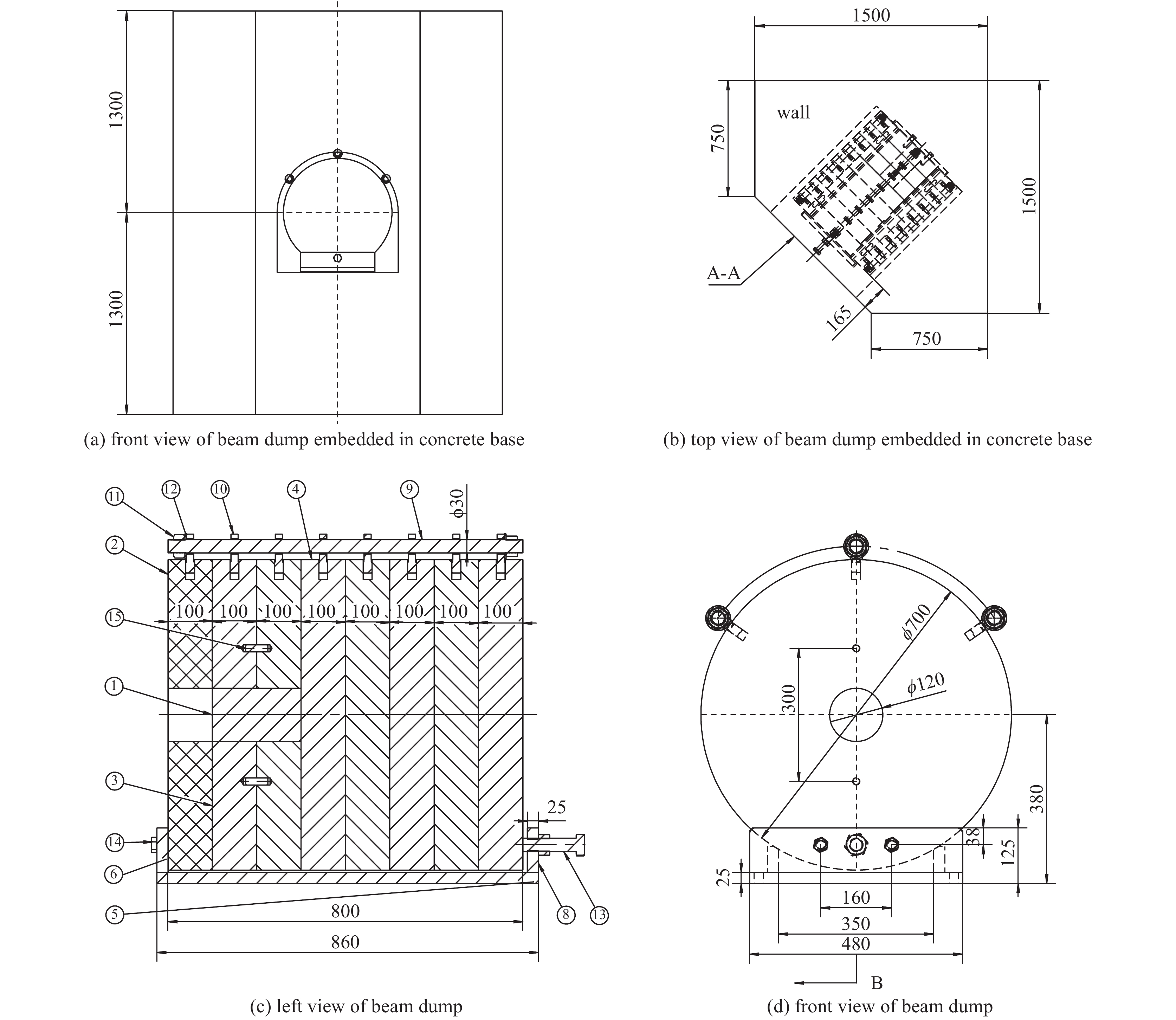
No.	important position	remnant beam/%	normalization parameter	path length/cm	path length after interaction point/cm	beam energy/MeV	γ
①	origin point	100.000	0.00038	0.00	—	5	9.785
②	YAG1	99.962	0.00064	67.00	—	5	9.785
③	start of acceleration1	99.898	0.00170	180.00	—	5	9.785
④	end of acceleration1	99.727	0.00057	480.00	—	50	97.847
⑤	YAG2	99.670	0.00019	581.00	—	50	97.847
⑥	start of acceleration 2	99.651	0.00170	614.00	—	50	97.847
⑦	end of acceleration 2	99.481	0.00030	914.00	—	95	185.91
⑧	YAG3	99.450	0.00040	967.00	—	95	185.91
⑨	YAG4	99.411	0.00147	1037.00	—	95	185.91
⑩	interaction point	99.263	0.00139	1296.00	0.00	95	185.91
⑪	YAG5	99.124	0.00015	1541.00	245.00	95	185.91
⑫	start of bending magnetic field	99.109	0.00043	1568.10	272.10	95	185.91
⑬	YAG6	99.066	0.00055	1644.10	348.10	95	185.91
⑭	front end of beam dump	99.011	0.99011	1740.75	444.75	95	185.91

下载: 导出CSV

No.	important position	normalized divergence/ (mm·mrad⁻¹)	geometric divergence/ (mm·mrad⁻¹)	beam size/ mm(rms)	beam size/cm (FWHM)	divergence angle/ mrad	divergence angle/mrad (FWHM)
①	origin point	0.20000	0.02044	0.25000	0.05888	0.08176	0.19254
②	YAG1	0.21551	0.02203	0.23785	0.05601	0.09260	0.21807
③	start of acceleration1	0.24167	0.02470	0.21736	0.05119	0.11363	0.26759
④	end of acceleration1	0.31111	0.00318	0.16296	0.03838	0.01951	0.04595
⑤	YAG2	0.33449	0.00342	0.14465	0.03406	0.02363	0.05566
⑥	start of acceleration 2	0.34213	0.00350	0.13867	0.03266	0.02522	0.05938
⑦	end of acceleration 2	0.41157	0.00221	0.08427	0.01984	0.02627	0.06187
⑧	YAG3	0.42384	0.00228	0.07466	0.01758	0.03054	0.07192
⑨	YAG4	0.44005	0.00237	0.06196	0.01459	0.03820	0.08996
⑩	interaction point	0.50000	0.00269	0.01500	0.00353	0.17930	0.42225
⑪	YAG5	0.50000	0.00269	0.43929	0.10345	0.17930	0.42225
⑫	start of bending magnetic field	0.50000	0.00269	0.48788	0.11489	0.17930	0.42225
⑬	YAG6	0.50000	0.00269	0.62415	0.14699	0.17930	0.42225
⑭	front end of beam dump	0.50000	0.00269	0.79744	0.18780	0.17930	0.42225

下载: 导出CSV

参考文献(16)

[1]	赵振堂, 高杰. 高能粒子对撞机加速器物理与设计[M]. 上海: 上海交通大学出版社, 2020 Zhao Zhentang, Gao Jie. Physics and design for accelerators of high energy particle colliders[M]. Shanghai: Shanghai Jiao Tong University Press, 2020
[2]	李成龙, 汤振兴, 裴元吉. 低发射度L波段光阴极微波电子枪物理设计[J]. 核技术, 2016, 39:090203. (Li Chenglong, Tang Zhenxing, Pei Yuanji. Physical design of low-emittance L-band photocathode microwave electron gun[J]. Nuclear Techniques, 2016, 39: 090203 doi: 10.11889/j.0253-3219.2016.hjs.39.090203
[3]	陈佳洱. 加速器物理基础[M]. 北京: 北京大学出版社, 2012. (Chen Jia’er. Physics basics of accelerator[M]. Beijing: Peking University Press, 2012))
[4]	方锦清, 陈关荣. 强流加速器中的束晕-混沌现象的定性分析[J]. 中国原子能科学研究院年报, 2000:69-70. (Fang Jinqing, Chen Guanrong. Qualitative analysis of beam halo chaos in high current accelerator[J]. Annual Report for China Institute of Atomic Energy, 2000: 69-70
[5]	何丽娟. 高能电子直线加速器(NSRL Linac)感生放射性研究[D]. 合肥: 中国科学技术大学, 2016: 7-30 He Lijuan. Induced radioactivity research of high-energy electron linear accelerator (NSRL Linac)[D]. Hefei: University of Science and Technology of China, 2016: 7-30
[6]	GB 5172-1985, 粒子加速器辐射防护规定[S] GB 5172-1985, The rule for radiation protection of particle accelerators[S]
[7]	HJ 979-2018, 电子加速器辐照装置辐射安全和防护[S] HJ 979-2018, Radiation safety and protection on electron accelerator irradiation facilities[S]
[8]	邱睿, 李君利, 武祯, 等. 四种蒙特卡罗程序的比较计算[J]. 原子能科学技术, 2008, 42(12):1149-1152. (Qiu Rui, Li Junli, Wu Zhen, et al. Comparison calculation of four Monte-Carlo codes[J]. Atomic Energy Science and Technology, 2008, 42(12): 1149-1152
[9]	Diamond W T, Ross C K. Actinium-225 production with an electron accelerator[J]. Journal of Applied Physics, 2021, 129: 104901. doi: 10.1063/5.0043509
[10]	Huang Mingyang. Study of accelerator neutrino detection at a spallation source[J]. Chinese Physics C, 2016, 40: 063002. doi: 10.1088/1674-1137/40/6/063002
[11]	Perillo-Marcone A, Calviani M, Solieri N, et al. Design and operation of the air-cooled beam dump for the extraction line of CERN's Proton Synchrotron Booster[J]. Physical Review Accelerators and Beams, 2020, 23: 063001. doi: 10.1103/PhysRevAccelBeams.23.063001
[12]	Ganter R. SwissFEL conceptual design report[R]. PSI Bericht 10-04, 2011: 10-04.
[13]	Ahdida C, Bozzato D, Calzolari D, et al. New capabilities of the FLUKA multi-purpose code[J]. Frontiers in Physics, 2022, 9: 788253. doi: 10.3389/fphy.2021.788253
[14]	Battistoni G, Boehlen T, Cerutti F, et al. Overview of the FLUKA code[J]. Annals of Nuclear Energy, 2015, 82: 10-18. doi: 10.1016/j.anucene.2014.11.007
[15]	Vlachoudis V. FLAIR: a powerful but user friendly graphical interface for FLUKA[C]//Proceedings of International Conference on Mathematics, Computational Methods & Reactor Physics. New York: American Nuclear Society, 2009, 2: 790-800.
[16]	Kutcher G J. Radiation protection design guidelines for 0.1 to 100 MeV particle accelerator facilities[J]. Medical Physics, 1978, 5(1): 73. doi: 10.1118/1.594404