中子在大气中产生氮俘获γ的蒙特卡罗模拟研究

刘利; 左应红; 牛胜利; 朱金辉; 李夏至

doi:10.11884/HPLPB202234.220055

中子在大气中产生氮俘获γ的蒙特卡罗模拟研究

doi: 10.11884/HPLPB202234.220055

刘利^1,,
左应红¹,
牛胜利¹,
朱金辉¹,
李夏至^{1, 2}

1.
西北核技术研究所，西安 710024
2.
中国科学技术大学地球和空间科学学院，合肥 230026

基金项目: 强脉冲辐射环境模拟与效应国家重点实验室专项经费项目（SKLIPR.1504）

详细信息

作者简介:
刘　利，liuli@nint.ac.cn

中图分类号: TL99
计量
- 文章访问数: 667
- HTML全文浏览量: 280
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2022-02-25
- 修回日期: 2022-04-22
- 录用日期: 2022-04-28
- 网络出版日期: 2022-04-29
- 刊出日期: 2022-08-15

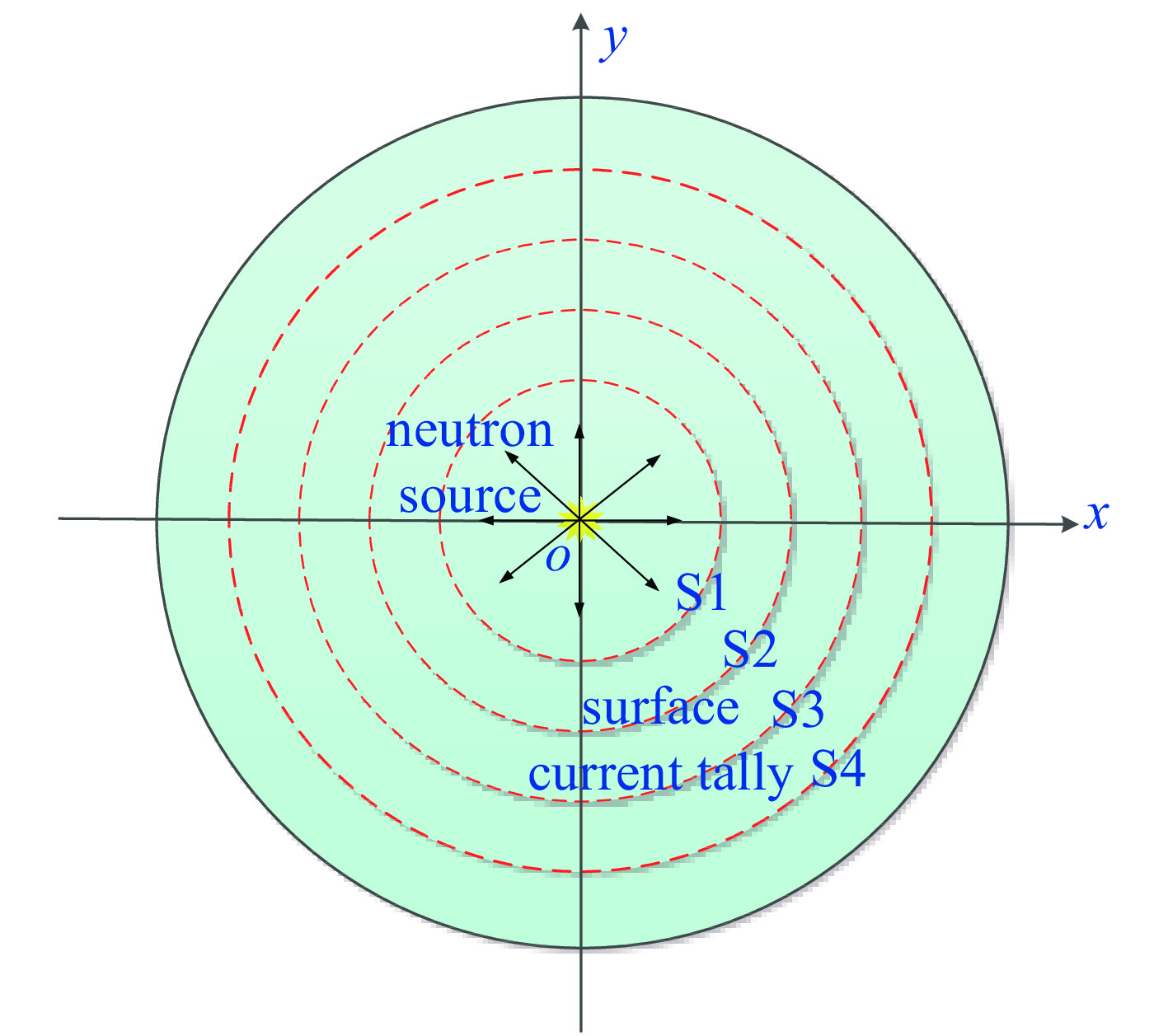
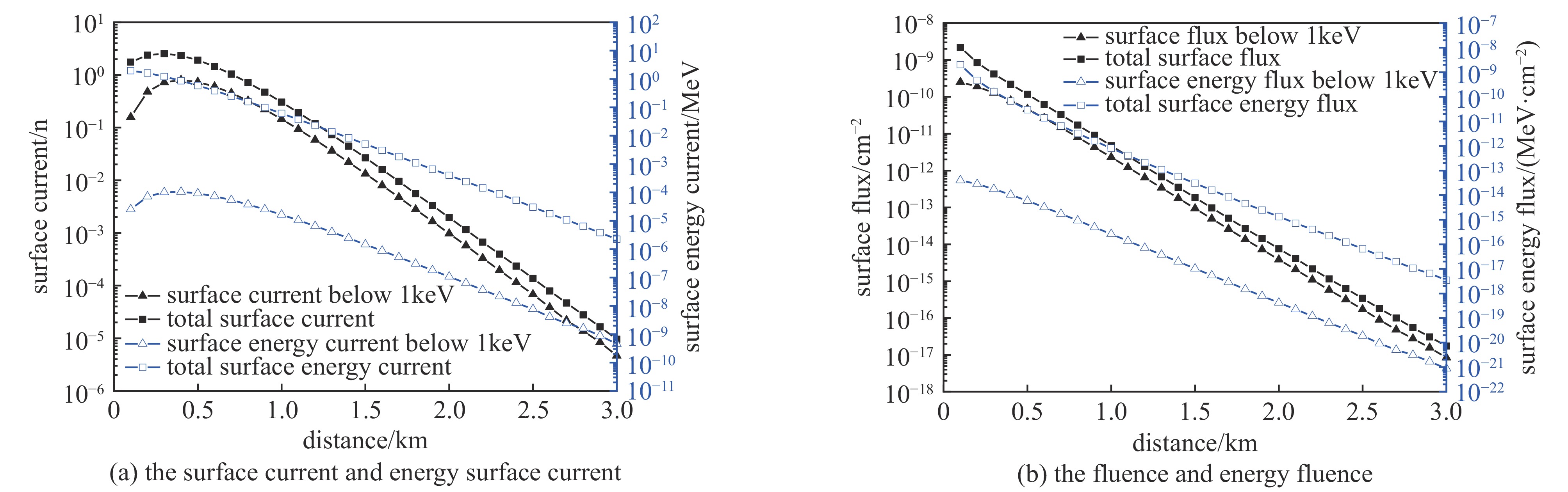
Monte Carlo simulation of neutron capture γ-rays from nitrogen in the atmosphere

1.
Northwest Institute of Nuclear Technology, Xi’an 710024, China
2.
School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China

摘要

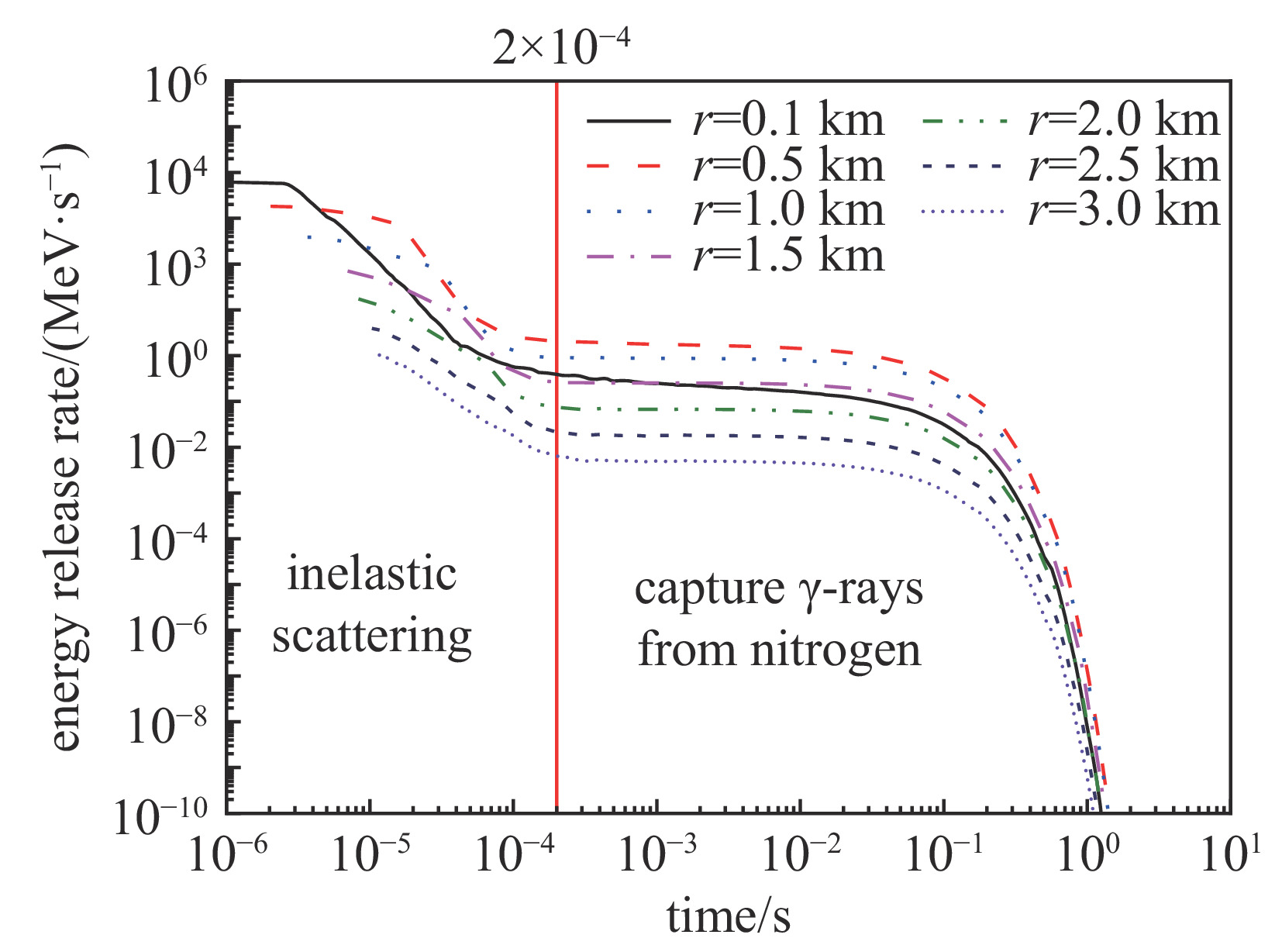
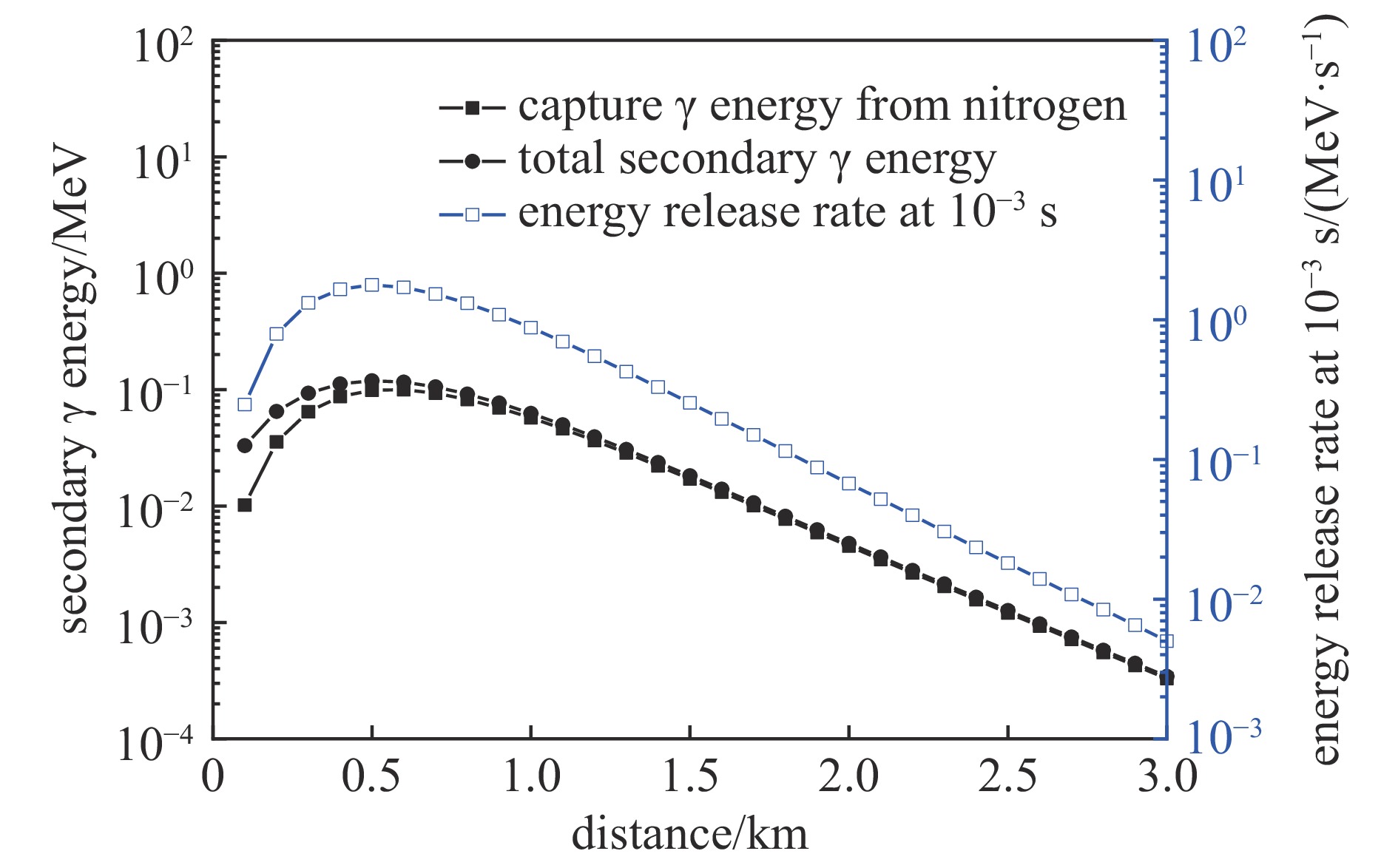
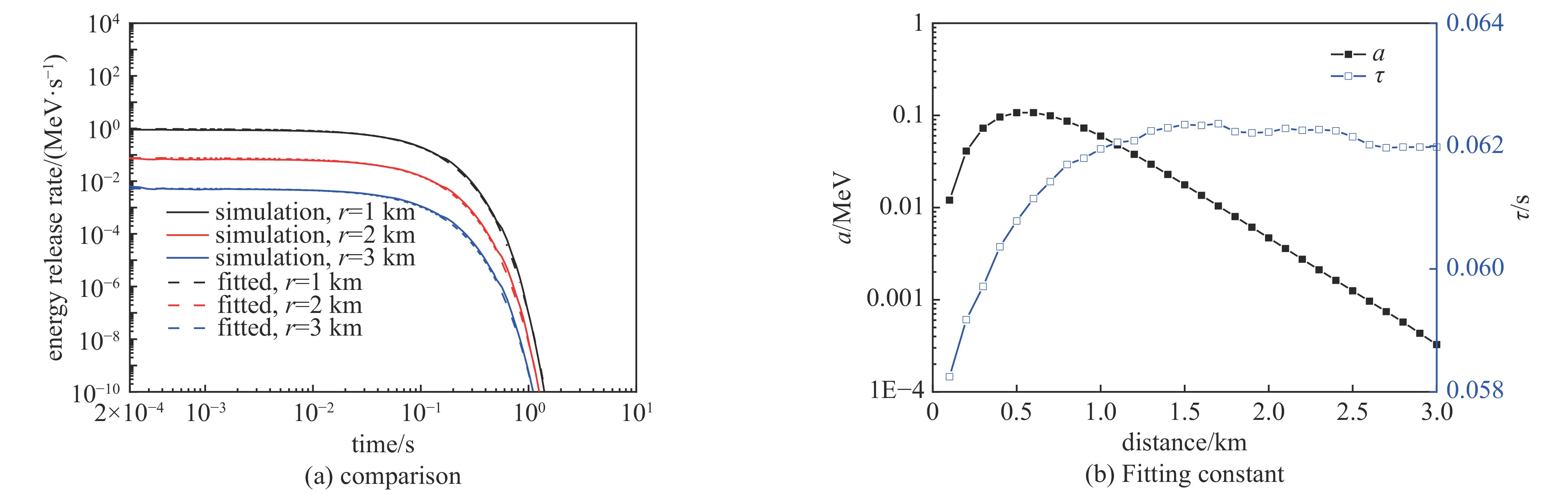
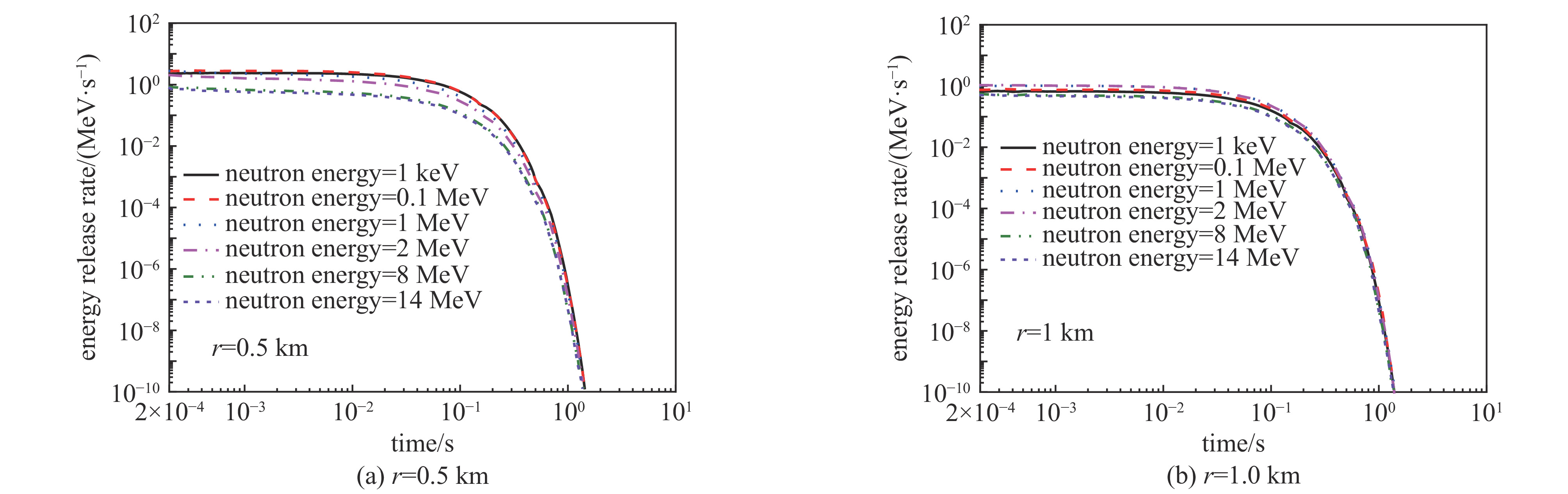
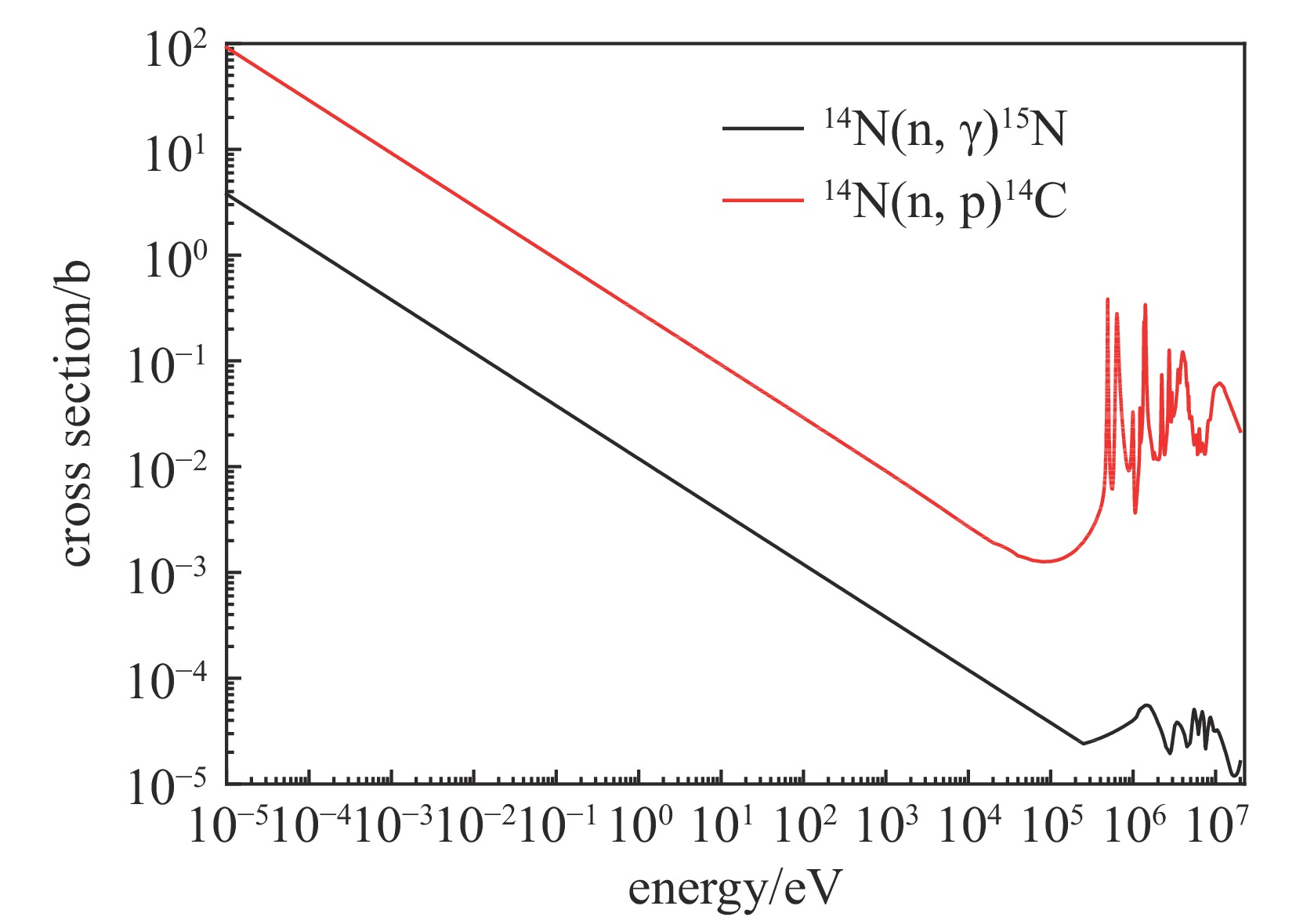
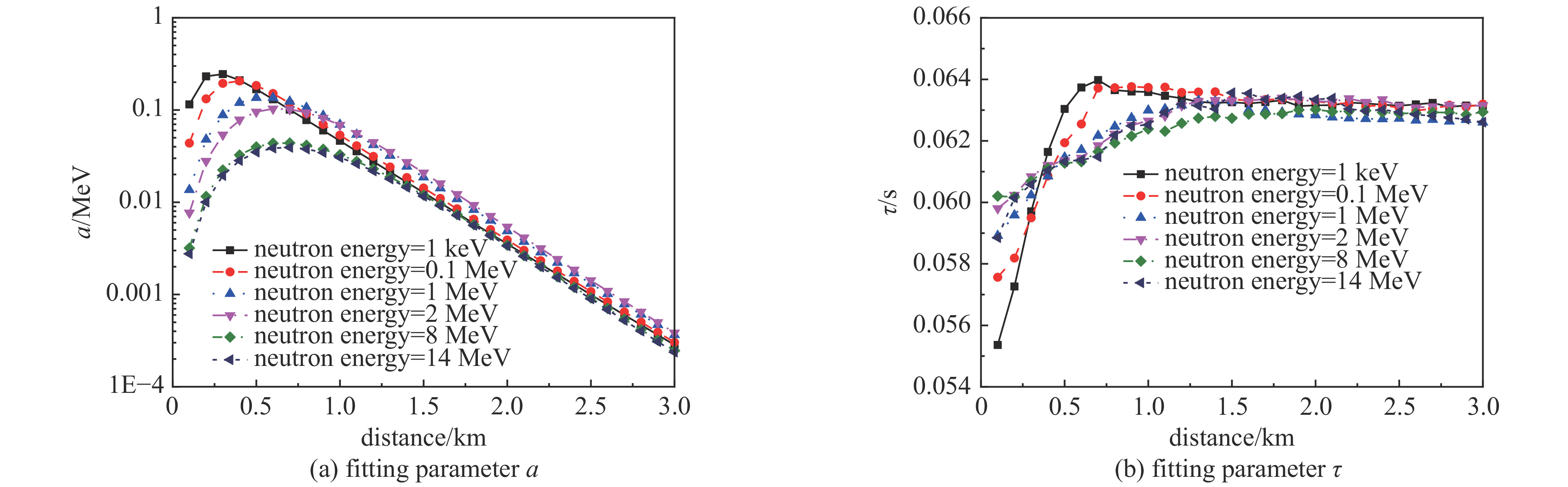
摘要: 为了精确计算早期核辐射，建立了中子及次级γ在大气中输运的蒙特卡罗计算模型，并利用几何分裂算法与时间分裂算法等减方差技巧提高计算效率，计算得到了距源点不同距离球面上中子与中子次级γ的信息，给出了不同位置不同时间的氮俘获γ能量释放率。开展了氮俘获γ能量释放率的规律性研究，并分析了中子能量对氮俘获γ的影响。结果表明，氮俘获γ能量释放率先随源点的距离增加而增大，在距源点约500 m达到峰值，而后随距离增加指数衰减。氮俘获γ能量释放率在时间上服从指数衰减规律，衰减时间在0.1 s左右。引入表征氮俘获γ辐射强度参数a和特征衰减时间参数$ \tau $，拟合得到了不同距离不同时间氮俘获γ能量释放率的快速计算公式。研究表明，氮俘获γ辐射强度、衰减时间及其空间分布均与中子能量密切相关。
- 氮俘获γ /
- 能量释放率 /
- 中子大气输运 /
- 蒙特卡罗方法
Abstract: Neutron capture γ-rays from nitrogen is an important part of initial nuclear radiation. To accurately calculate the early nuclear radiation, the Monte Carlo computing model for the neutron and secondary γ-rays transport in the atmosphere is established. Some variance reduction techniques, such as geometric splitting algorithm and time splitting algorithm are used in the Monte Carlo method to improve computing efficiency. The neutron and secondary γ-rays information on the spherical surface at different distances are calculated. The energy release rates of capture γ-rays from nitrogen at different positions and at different times are given. The regularity of the energy release rate of capture γ-rays from nitrogen is studied, and the influence of neutron energy on capture γ-rays from nitrogen is analyzed. The results show that the energy release rate of capture γ from nitrogen increases with the increase of distance from the source at first, reaches the peak at about 500 m from the source, and then decreases exponentially with the increase of distance. The energy release rate of capture γ-rays from nitrogen obeys exponential decay law in time, and the decay time is about 0.1 s. By introducing the parameter of a representing the radiation intensity and the characteristic attenuation time parameter of τ, a fast calculation formula for the energy release rate of capture γ-rays from nitrogen at different distances and times is obtained by fitting formulas. Results show that the intensity radiation, the decay time scale of capture γ-rays from nitrogen and their spatial distribution are closely related to neutron energy.
- neutron capture γ-ray from nitrogen /
- energy release rate /
- neutron transport in the atmosphere /
- Monte Carlo method

HTML全文

图 1 中子与¹⁴N的核反应截面

Figure 1. Reaction cross-section between neutron and ¹⁴N

下载: 全尺寸图片幻灯片

图 2 中子在大气中输运的几何模型

Figure 2. Geometry model of neutron transport in the atmosphere

下载: 全尺寸图片幻灯片

图 3 中子与低能中子面积分流和注量随距离变化

Figure 3. Neutron surface current and fluence vs. distances

下载: 全尺寸图片幻灯片

图 4 不同距离的中子次级γ能量释放率随时间变化

Figure 4. Neutron secondary gamma energy release rate vs time at different distances

下载: 全尺寸图片幻灯片

图 5 中子次级γ能量及能量释放率随距离变化

Figure 5. Neutron secondary gamma energy and energy release rate vs distances

下载: 全尺寸图片幻灯片

图 6 氮俘获γ能量释放率拟合参数公式

Figure 6. Fitting of neutron capture γ-ray energy release rate

下载: 全尺寸图片幻灯片

图 7 不同能量中子对氮俘获γ能量释放率随时间的变化

Figure 7. Neutron secondary gamma energy release rate vs. time for different neutron energy

下载: 全尺寸图片幻灯片

图 8 不同能量中子的氮俘获γ能量释放率拟合参数

Figure 8. Fitting parameters of neutron capture γ-ray energy release rate for different neutron energy

下载: 全尺寸图片幻灯片

表 1 采用不同减方差方法模拟所得γ注量率、相对误差及FOM因子

Table 1. Gamma ray fluence rate, relative error and FOM factor by using different variance reduction method

distance/km	method of variance reduction	fluence rate of γ at 1×10⁻² s /(10⁻³cm⁻²·s⁻¹)	relative error	FOM factor
2.0	none	59.8	8.1%	2.7
	time splitting	63.1	1.4%	3.5
	geometry splitting	62.4	2.3%	11
	time splitting + geometry splitting	62.2	0.6%	13
3.0	none	3.57	36%	0.14
	time splitting	4.77	5.3%	0.24
	geometry splitting	4.71	4.9%	2.4
	time splitting + geometry splitting	4.58	1.1%	3.2

下载: 导出CSV

表 2 不同距离球面处的中子及次级γ的平均能量

Table 2. Energy of neutron and secondary gamma at different distances

distance/km	neutron energy/MeV	gamma energy/MeV
0.1	0.92	1.54
0.3	0.39	1.46
0.5	0.26	1.46
1.0	0.17	1.33
1.5	0.16	1.24
2.0	0.18	1.24
2.5	0.20	1.27
3.0	0.23	1.32

下载: 导出CSV

参考文献(15)

[1]	Glasstone S, Dolan P J. The effects of nuclear weapons[M]. Washington: U. S. Department of Defense, 1977.
[2]	乔登江. 核爆炸物理概论[M]. 北京: 国防工业出版社, 2003 Qiao Dengjiang. Introduction to the physics of nuclear explosion[M]. Beijing: National Defense Industry Press, 2003
[3]	王建国, 牛胜利, 张殿辉, 等. 高空核爆炸效应参数手册[M]. 北京: 原子能出版社, 2010 Wang Jianguo, Niu Shengli, Zhang Dianhui, et al. Parameter handbook of high altitude nuclear detonation effect[M]. Beijing: Atomic Energy Press, 2010
[4]	刘晓红, 王伟力, 孟涛, 等. 早期核辐射毁伤效应空间建模及剖切算法[J]. 火力与指挥控制, 2012, 37(9):190-192,197 doi: 10.3969/j.issn.1002-0640.2012.09.051 Liu Xiaohong, Wang Weili, Meng Tao, et al. Research on 3D spatial data models for early nuclear radiation damage effects and slitting algorithm[J]. Fire Control & Command Control, 2012, 37(9): 190-192,197 doi: 10.3969/j.issn.1002-0640.2012.09.051
[5]	王泰春, 贺云汉, 王玉芝. 电磁脉冲导论[M]. 北京: 国防工业出版社, 2011 Wang Taichun, He Yunhan, Wang Yuzhi. Introduction to electromagnetic pulse[M]. Beijing: National Defense Industry Press, 2011
[6]	郭力生, 鲁华玉. 防原医学[M]. 北京: 原子能出版社, 2006 Guo Lisheng, Lu Huayu. Antigenic medicine[M]. Beijing: Atomic Energy Press, 2006
[7]	王瑞宏, 姬志成, 裴鹿成. 深穿透粒子输运问题的自适应抽样方法[J]. 强激光与粒子束, 2012, 24(12):2941-2945 doi: 10.3788/HPLPB20122412.2941 Wang Ruihong, Ji Zhicheng, Pei Lucheng. Adaptive sampling method in deep-penetration particle transport problem[J]. High Power Laser and Particle Beams, 2012, 24(12): 2941-2945 doi: 10.3788/HPLPB20122412.2941
[8]	郑征, 梅其良, 邓力. 全局减方差方法的HBR-2基准题应用[J]. 原子能科学技术, 2018, 52(6):987-993 doi: 10.7538/yzk.2017.youxian.0510 Zheng Zheng, Mei Qiliang, Deng Li. Global variance reduction method applied to HBR-2 benchmark[J]. Atomic Energy Science and Technology, 2018, 52(6): 987-993 doi: 10.7538/yzk.2017.youxian.0510
[9]	申靖文, 胡也, 郑俞, 等. 蒙特卡罗输运模拟软件JMCT的深穿透屏蔽计算[J]. 强激光与粒子束, 2018, 30:046002 doi: 10.11884/HPLPB201830.170222 Shen Jingwen, Hu Ye, Zheng Yu, et al. Three-dimensional Monte Carlo transport code JMCT in shielding engineering application[J]. High Power Laser and Particle Beams, 2018, 30: 046002 doi: 10.11884/HPLPB201830.170222
[10]	Booth T E. MCNP variance reduction examples[R]. LA-UR-12-25907, 2012.
[11]	史涛, 马纪敏, 邱有恒, 等. 基于蒙特卡罗正算输运的全局减方差方法[J]. 强激光与粒子束, 2018, 30:016006 doi: 10.11884/HPLPB201830.170163 Shi Tao, Ma Jimin, Qiu Youheng, et al. Global variance reduction based on forward Monte Carlo calculation[J]. High Power Laser and Particle Beams, 2018, 30: 016006 doi: 10.11884/HPLPB201830.170163
[12]	郑征, 丁谦学, 周岩. 基于共轭离散纵标的减方差方法[J]. 强激光与粒子束, 2018, 30:026004 doi: 10.11884/HPLPB201830.170223 Zheng Zheng, Ding Qianxue, Zhou Yan. Variance reduction method based on adjoint discrete ordinate[J]. High Power Laser and Particle Beams, 2018, 30: 026004 doi: 10.11884/HPLPB201830.170223
[13]	Culbertson C N, Hendricks J S. An assessment of the MCNP4C weight window[R]. LA-13668, 1999.
[14]	左应红, 牛胜利, 商鹏, 等. 权窗减方差方法在γ射线长距离输运模拟中的应用[J]. 现代应用物理, 2020, 11:010205 Zuo Yinghong, Niu Shengli, Shang Peng, et al. Weight window variance reduction method for simulating long distance γ-ray transport[J]. Modern Applied Physics, 2020, 11: 010205
[15]	刘利, 左应红, 牛胜利, 等. 中子及次级γ在高空长距离蒙特卡罗输运模拟中的减方差方法[J]. 现代应用物理, 2022, 13:010202 Liu Li, Zuo Yinghong, Niu Shengli, et al. A varaince reduction method for simulating the long-distance transport of neutrons and secondary γ in high-altitude atmosphere by Monte Carlo method[J]. Modern Applied Physics, 2022, 13: 010202