Simulation research on pulse steepening technology based on ferrite transmission line
-
摘要: 铁氧体传输线的脉冲陡化技术能够实现高频高功率快前沿脉冲输出，且具有固态化和紧凑化优点，已广泛应用于高功率微波源。关于铁氧体传输线脉冲陡化特性的仿真计算缺乏较为精确的模型，因此利用COMSOL仿真软件建立了铁氧体传输线仿真模型，考虑电磁波传播与磁芯磁化进动之间的相互影响，将Maxwell方程与Landau-Lifshitz-Gilbert （LLG）方程结合进行仿真计算，与实验结果进行对比验证了仿真模型的准确性。再在此模型基础上，研究了不同传输线长度、不同电压幅值，以及不同外加偏置磁场对脉冲波形的影响。结果表明：脉冲前沿随传输线长度的增大及电压幅值的增大而减小；外加偏置磁场对脉冲前沿有影响，选择合适的外加偏置磁场可以实现最小脉冲前沿输出。Abstract: The pulse steepening technology of ferrite transmission lines can realize high-frequency and high-power fast front pulse output and has the advantages of solid-state and compactness. It has been widely used in high-power microwave sources. The simulation calculation of pulse steepening characteristics of ferrite transmission lines lacks a more accurate model. Therefore, this paper establishes the simulation model of the ferrite transmission line by using COMSOL simulation software, considering the interaction between electromagnetic wave propagation and magnetic core magnetization precession. The Maxwell equation and Landau-Lifshitz-Gilbert (LLG) equation are combined for simulative calculation. Compared with the experimental results, the accuracy of the simulation model is verified. Based on this model, simultaneous interpreting of the effect of different transmission line lengths, voltage amplitude, and external bias magnetic field on pulse waveform is studied. The results show that the pulse front decreases with the increase of transmission line length and the increase of voltage amplitude; The output of the minimum pulse front can be realized by selecting an appropriate external bias magnetic field.
-
Key words:
- ferrite transmission line /
- COMSOL /
- Maxwell equation /
- LLG equation /
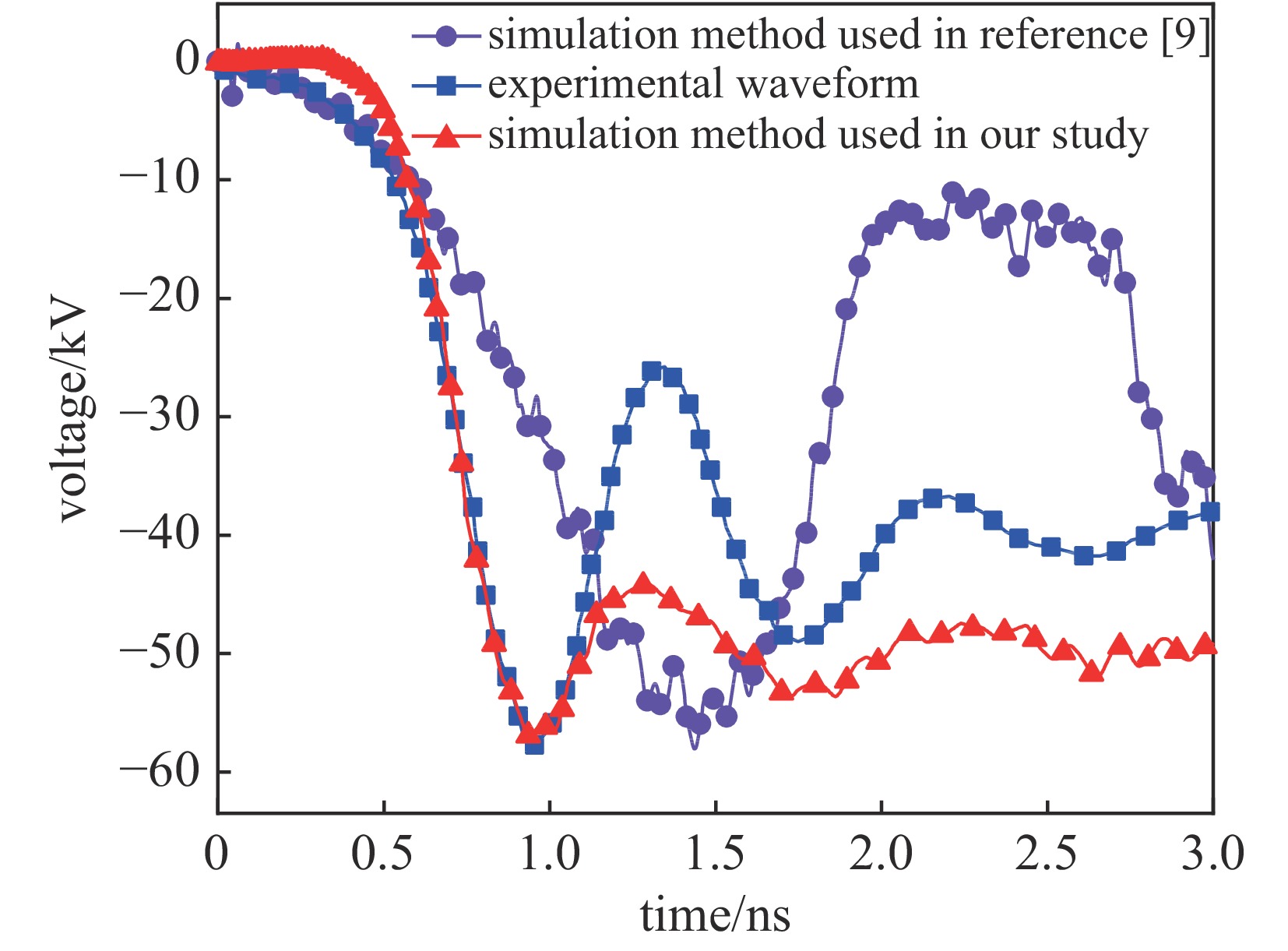
- pulse front steepening
-
图 1 铁氧体传输线陡化的宏观解释
Figure 1. Macroscopic explanation of the steepening of ferrite transmission line
图 3 传输线结构及电路模型示意图
Figure 3. Schematic diagram of transmission line structure and circuit model
图 6 输入电压50 kV模拟与实验输出波形对比图
Figure 6. 50 kV comparison diagram of analog and experimental output waveforms
图 11 不同偏置磁场的仿真输出波形图
Figure 11. Simulation output waveforms of different bias magnetic fields
图 12 不同偏置磁场的10%～90%电压上升时间
Figure 12. 10%～90% voltage rise time of different bias magnetic field
表 2 GNLTL材料属性
Table 2. GNLTL material properties
material $\mu $ $\varepsilon $ brass 1 1 Ni-Zn ferrite 4.8 14 SF6 1 1 
下载: 导出CSV
-
[1] French D M, Hoff B W. Spatially dispersive ferrite nonlinear transmission line with axial bias[J]. IEEE Transactions on Plasma Science, 2014, 42(10): 3387-3390. doi: 10.1109/TPS.2014.2348492 [2] Romanchenko I V, Rostov V V, Gunin A V, et al. High power microwave beam steering based on gyromagnetic nonlinear transmission lines[J]. Journal of Applied Physics, 2015, 117: 214907. doi: 10.1063/1.4922280 [3] Reale D V, Parson J M, Neuber A A, et al. Investigation of a stripline transmission line structure for gyromagnetic nonlinear transmission line high power microwave sources[J]. Review of Scientific Instruments, 2016, 87: 034706. doi: 10.1063/1.4942246 [4] Ulmaskulov M R, Mesyats G A, Sadykova A G, et al. Energy compression of nanosecond high-voltage pulses based on two-stage hybrid scheme[J]. Review of Scientific Instruments, 2017, 88: 045106. doi: 10.1063/1.4979641 [5] Katayev I G. Electromagnetic shock waves[M]. London: Iliffe Books Ltd. , 1923. [6] Pouladian-Kari R, Benson T M, Shapland A J, et al. The electrical simulation of pulse sharpening by dynamic lines[C]//Proceedings of the 7th Pulsed Power Conference. IEEE, 1989. [7] Dolan J E. Simulation of shock waves in ferrite-loaded coaxial transmission lines with axial bias[J]. Journal of Physics D: Applied Physics, 1999, 32(15): 1826-1831. doi: 10.1088/0022-3727/32/15/310 [8] 俞建国. 基于铁氧体传输线的脉冲陡化技术研究[D]. 西安: 西安电子科技大学, 2010: 9-13Yu Jianguo. Research of pulse sharpening based on ferrite line[D]. Xi'an: Xidian University, 2010: 9-13 [9] 乔中兴, 刘恺, 董寅. 铁氧体同轴传输线脉冲锐化特性的研究[J]. 电工技术学报, 2015, 30(s2):21-25. (Qiao Zhongxing, Liu Kai, Dong Yin. Investigation of ferrite-filled coaxial transmission lines for pulse sharpening[J]. Transactions of China Electrotechnical Society, 2015, 30(s2): 21-25Qiao Zhongxing, Liu Kai, Dong Yin. Investigation of ferrite-filled coaxial transmission lines for pulse sharpening[J]. Transactions of China Electrotechnical Society, 2015, 30(s2): 21-25 [10] 张兴家, 卢彦雷, 樊亚军, 等. 一种三传输线型亚纳秒脉冲压缩装置[J]. 强激光与粒子束, 2017, 29:115002. (Zhang Xingjia, Lu Yanlei, Fan Yajun, et al. Triple transmission line type subnanosecond pulse-compression device[J]. High Power Laser and Particle Beams, 2017, 29: 115002 doi: 10.11884/HPLPB201729.170101Zhang Xingjia, Lu Yanlei, Fan Yajun, et al. Triple transmission line type subnanosecond pulse-compression device[J]. High Power Laser and Particle Beams, 2017, 29: 115002 doi: 10.11884/HPLPB201729.170101 [11] Tie Weihao, Meng Cui, Zhao Chengguang, et al. Optimized analysis of sharpening characteristics of a compact RF pulse source based on a gyro-magnetic nonlinear transmission line for ultrawideband electromagnetic pulse application[J]. Plasma Science and Technology, 2019, 21: 095503. doi: 10.1088/2058-6272/ab2626 [12] 铁维昊, 赵程光, 孟萃, 等. 旋磁型非线性传输线调制脉冲特性数值分析[J]. 高电压技术, 2019, 45(1):301-309. (Tie Weihao, Zhao Chengguang, Meng Cui, et al. Numerical analysis on modulated RF pulse characteristics of gyro-magnetic nonlinear transmission line[J]. High Voltage Engineering, 2019, 45(1): 301-309Tie Weihao, Zhao Chengguang, Meng Cui, et al. Numerical analysis on modulated RF pulse characteristics of gyro-magnetic nonlinear transmission line[J]. High Voltage Engineering, 2019, 45(1): 301-309 [13] Greco A F G, Rossi J O, Yamasaki F S, et al. 1D-FDTD simulation of microwave generation using ferrite electromagnetic shock lines[C]//Proceedings of 2020 IEEE Electrical Insulation Conference (EIC). IEEE, 2020. [14] 方旭, 潘亚峰, 丁臻捷, 等. 非线性铁氧体传输线的脉冲陡化作用[J]. 强激光与粒子束, 2014, 26:115006. (Fang Xu, Pan Yafeng, Ding Zhenjie, et al. Pulse sharpening effect of nonlinear ferrite-loaded transmisstion line[J]. High Power Laser and Particle Beams, 2014, 26: 115006 doi: 10.11884/HPLPB201426.115006Fang Xu, Pan Yafeng, Ding Zhenjie, et al. Pulse sharpening effect of nonlinear ferrite-loaded transmisstion line[J]. High Power Laser and Particle Beams, 2014, 26: 115006 doi: 10.11884/HPLPB201426.115006 [15] 胡月川. 铁磁纳米管中的磁化强度动力学[D]. 天津: 河北工业大学, 2016: 3-9Hu Yuechuan. The magnetization dynamics in magnetic nanotubes[D]. Tianjin: Hebei University of Technology, 2016: 3-9 [16] 宛德福, 马兴隆. 磁性物理学[M]. 成都: 电子科技大学出版社, 1994: 437-441Wan Defu, Ma Xinglong. Magnetic physics[M]. Chengdu: University of Electronic Science and Technology of China Press, 1994: 437-441 [17] Gilbert T L. A phenomenological theory of damping in ferromagnetic materials[J]. IEEE Transactions on Magnetics, 2004, 40(6): 3443-3449. doi: 10.1109/TMAG.2004.836740 -
点击查看大图
图(12) / 表(2)
计量
- 文章访问数: 622
- HTML全文浏览量: 216
- PDF下载量: 65
- 被引次数: 0
