磷酸二氢钾（KH₂PO₄，简称KDP）晶体具有良好的光电性能，其损伤阈值高且能够生长成大尺寸晶体，是目前唯一可用于惯性约束聚变（ICF）研究的非线性晶体材料。在工程应用中，其光学元件的实际损伤阈值远低于理论值，限制了激光的输出能量，降低了元器件的使用寿命。磷酸二氢铵（NH₄H₂PO₄，简称ADP）晶体是KDP的同类晶体，两者具有相似的晶体结构，在四倍频方面有更广阔的应用。

缺陷是现阶段影响晶体损伤阈值的主要因素。研究表明，不仅本征点缺陷对晶体损伤有重要影响，金属杂质离子在很大程度上也会影响晶体的光学性能及损伤阈值^[1-8]。2001年，Garces等研究者^[9]利用电子顺磁共振的方法研究了掺Fe的KDP晶体的光学吸收和电荷转移情况，他们认为Fe在270 nm附近引入的吸收峰是由Fe³⁺取代K⁺引起，200～300 nm的吸收峰主要由Fe取代P原子形成FeO₄²⁻分子基团引起。2002年，Eremina等研究者^[10-12]在晶体化学分析和KDP晶体结构模型的基础上分析了二价金属离子（Ni²⁺, Co²⁺, Fe²⁺, Mn²⁺）和三价金属离子（Al³⁺, Fe³⁺, Mn³⁺, Y³⁺, La³⁺）对于KDP晶体结构及光学质量的影响，他们认为二价金属离子主要影响晶体结构而三价金属离子主要影响晶体的光学吸收性质。2005年，他们利用实验方法研究了这类掺杂离子对KDP晶体生长动力学和表面形貌的影响^[4]。同年，王波等研究者^[13-14]研究了Fe³⁺对KDP晶体生长的影响，发现一定浓度的掺杂量可以提高溶液的稳定性，且Fe³⁺对晶体柱面的影响较大。

晶体生长的原料中存有多种微量杂质离子，Fe是最常见最具代表性的金属杂质离子，其对晶体性能的影响不容忽视。然而，由于实验技术手段的限制，Fe掺杂缺陷对晶体性能及损伤的影响机制尚不明确，实验推测并没有得到明确证实。2017年，Liu等研究者^[15]利用第一性原理方法研究了掺杂Fe³⁺缺陷对KDP晶体的电子结构及光学性质的影响。尽管KDP晶体的此类研究取得了一定的成果，但这类点缺陷及其引入的团簇缺陷对晶体的能量、微观应力以及磁性的影响尚未可知。与此同时，ADP作为KDP晶体的同类晶体，金属离子及其团簇缺陷对其晶体结构以及性能的影响亦不容忽视，杂质离子对于两种晶体损伤阈值的影响差异也尚不清楚。因此，本文将采用第一性原理方法，探究掺杂Fe的点缺陷及其部分团簇缺陷对KDP和ADP晶体结构、能量、微观应力、电子结构和光吸收性质的影响。

1.   理论计算方法

本文采用了基于密度泛函理论的VASP软件进行理论模拟。计算中价电子和原子核的相互作用选用投影缀加波（PAW）。K、H、P、O、N、Fe原子的价电子分别为K 4s¹、H 1s¹、P 3s²sp³、O 2s²2p⁴、N 2s²sp³、Fe 3d⁶4s²，其中在点缺陷的研究中Fe原子考虑顺磁（NM）、铁磁（FM）和反铁磁（AFM）的状态^[16-30]。采用Monkhorst-Pack方法选取布里渊区k空间网格点来进行积分^[26]。为了提高计算效率，KDP晶体的计算参数依据文献选取，对ADP晶体的计算参数进行了收敛性测试^[27-30]。对KDP晶体原有的晶格常数^[31] a = b = 0.75 nm ，c = 0.697 nm和ADP晶体原有晶格常数^[32] a = b = 0.75 nm，c = 0.755 nm重新定义了晶格矢量^[29]，即

建立含有8个KDP分子(包含64个原子)和4个ADP分子(含有48个原子)的超胞，在团簇缺陷的研究中，建立含有32个KDP分子（包含256个原子）和32个ADP分子（含有384个原子）的超胞。截断能分别设置为680 eV和400 eV。计算中电子交换相关势选用GGA-PBE泛函来优化晶体的结构^[33]，选用HSE06泛函来进行能量和电子性质的计算^[34-35]。HSE06泛函中屏蔽距离和混合参数分别固定为1 nm和0.25。相对应点缺陷的k点^[29]分别设置为4×4×4和2×2×2，团簇缺陷的k点选为1×1×1。对晶胞参数和晶胞内的原子坐标均进行了结构弛豫，达到了收敛标准使受力小于0.1 eV/nm。在ADP晶体的计算中加入范德华修正项DFT/vdW-WF2来考虑晶体中氢键的作用^[36-38]。

2.   结果与讨论

室温下，KDP和ADP晶体都属于四方晶系，$D_{2{{d}}}^{12} - I\mathop 4\limits^ - 2{{d}}$空间群^[31]。为确保研究模型和结果的准确性，构建了缺陷可能存在的位点，以确定Fe原子进入KDP和ADP晶体后结构稳定的最佳位置。在模型构建中分别从晶胞中移除一个H、K和P原子，并将Fe原子添加到相应位置，除此之外，将Fe原子加入到间隙位置，分别得到Fe取代H (Fe_H)、Fe取代K (Fe_K)、Fe取代P (Fe_P) 和Fe间隙 (Fe_i) 模型，并计算缺陷形成能，如表1所示。计算缺陷形成能时，采用常温常压下稳定化合物Fe₂O₃来计算Fe元素的化学势，表达式为

表  1  KDP晶体中Fe取代不同位点的模型体系的缺陷形成能

Table  1.  Defect formation energies of the KDP crystal with Fe in different locations

location	defect formation energy/eV
FeH	8.7
FeP	2.74
FeK	12.59
Fei	16.10

下载: 导出CSV 

| 显示表格

式中：Fe₂O₃为三方晶系，空间群为R-3c。计算得到Fe的化学势为−16.40 eV。从表中可以看出，在KDP晶体中，Fe原子取代P原子形成的Fe_P缺陷具有最低的缺陷形成能，为2.74 eV, 明显低于Fe取代其他位置的缺陷形成能。尽管Fe与K原子的原子半径相差相对较小，但其取代K原子的缺陷形成能明显大于取代H原子的缺陷形成能。Fe原子在间隙位置形成的缺陷形成能最大，结构最不稳定，主要由于Fe原子本身的原子半径较大，在间隙位置出现引起晶体产生极大的晶格畸变致使结构不稳定。ADP是KDP的同类晶体，两者具有相似的晶体结构，通过对晶体中点缺陷形成能的计算结果可知，在ADP晶体中各缺陷的形成能大小的总体趋势与KDP晶体相同，只是具体数值有所差异，可以认为在ADP晶体中Fe_P缺陷也有最低的缺陷形成能，因此后续只研究了Fe_P缺陷。除构筑点缺陷外，在计算中考虑了Fe取代P原子形成点缺陷后与周围缺陷形成复合缺陷的情况，通过电荷补偿形成Fe_P缺陷与V_O缺陷同时存在^[32]，在此基础上，通过去掉与V_O缺陷相连的H原子，构成Fe_P与V_OH缺陷同时存在的环境，计算了缺陷的形成能，如表2所示。通过结果可以看出，晶体中存在Fe_P与V_OH团簇缺陷的几率很小，其形成能分别为24.38 eV和16.41 eV，比晶体中点缺陷的形成能高很多，因此可以认为晶体中不会存在这种形式的团簇缺陷，因此在后续计算中不予考虑。

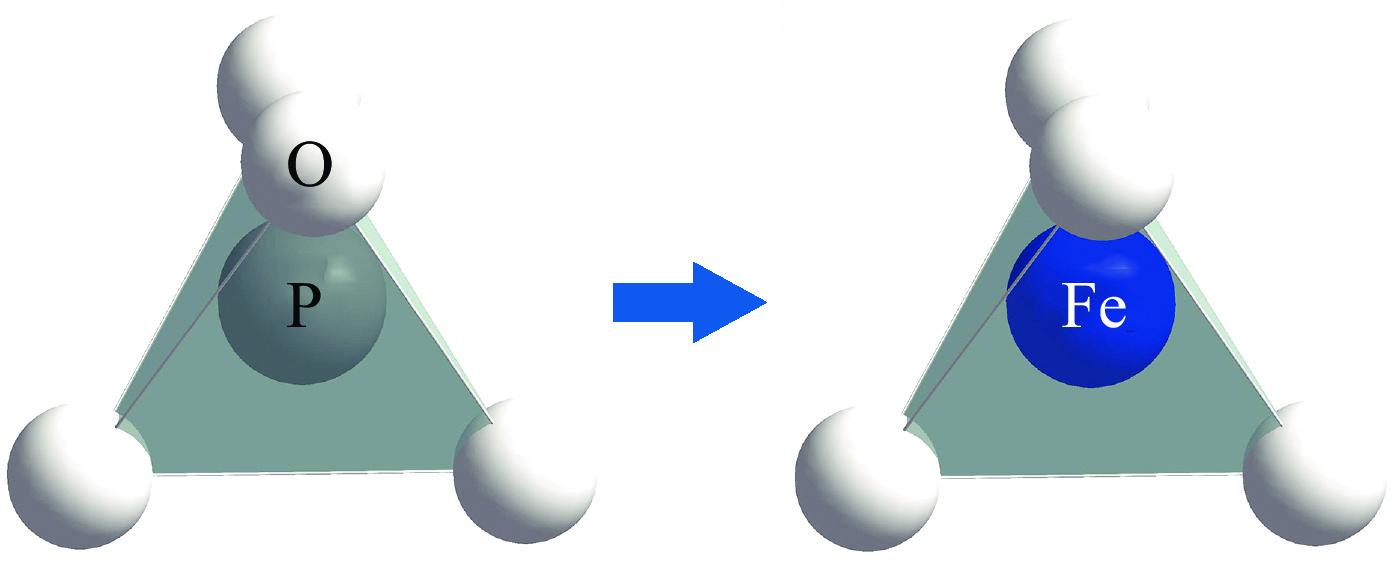
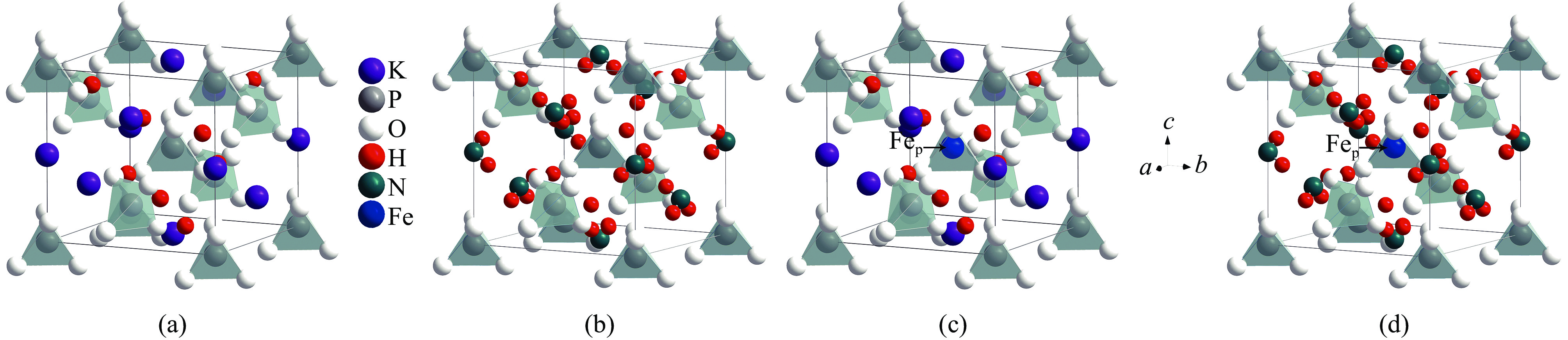
表  2  KDP和ADP晶体中Fe团簇缺陷的缺陷形成能

Table  2.  Defect formation energies of the KDP crystal with Fe atom in different locations

defect	defect formation energy/eV
	KDP	ADP
VOH	8.56	0.15
FeP+VOH	24.38	16.41

下载: 导出CSV 

| 显示表格

Fe_P缺陷的取代基团结构如图1和图2所示，在KDP晶体中，移除的P原子处在PO₄³⁻骨架结构中，Fe_P的位置为（0.500, 0.500, 0.500），缺陷浓度为1.56%。在ADP晶体中，Fe_P的位置也为（0.500, 0.500, 0.500），缺陷浓度为2.08%。带电荷的缺陷模型是在中性缺陷体系中加入或去除相应数量的电子得到的，所有的结构均进行了优化。

图  1  完美KDP和ADP晶体及其FeP缺陷的结构模型

Figure  1.  Crystal structures of the pristine KDP (a) and ADP (b) as well as the crystals with FeP (c, d) defects

下载: 全尺寸图片 幻灯片

图  2  Fe替代P原子的结构示意图

Figure  2.  Schematic diagram of the structure for Fe replacing P atom

下载: 全尺寸图片 幻灯片

从图中可以看出，KDP和ADP晶体中的化学键没有明显改变。只有处于中心区域的PO₄骨架结构转变为FeO₄基团结构。为分析掺杂取代之后的结构变化，研究了顺磁（NM）、铁磁（FM）和反铁磁（AFM）条件下的Fe−O键的键长变化，如表3所示。可以看出，无论是顺磁、铁磁或是反铁磁时，在同一磁性条件下随缺陷得电子数量的增加，KDP和ADP晶体中Fe−O键的键长不断增长，Fe原子与周围O原子形成的Fe−O键的键强减弱。例如，在顺磁（NM）条件下，随着Fe_P缺陷得电子数量增加，KDP晶体中Fe−O键的键长变化率分别为4.52%，5.16%，7.10%和9.68%。在同磁性同电荷条件下，由于晶体结构的相似性，KDP和ADP晶体中的Fe−O键的键长相差较小，仅为0.01 eV。不同磁性状态对于两晶体同电荷状态下的Fe−O键键长的影响几乎不变，可以认为磁性状态对于晶体结构几乎没有影响。可以看出在铁磁条件下KDP晶体中的Fe_P²⁻缺陷的Fe−O键键长的变化相对较大，说明在此情况下，结构产生较大的晶格畸变。

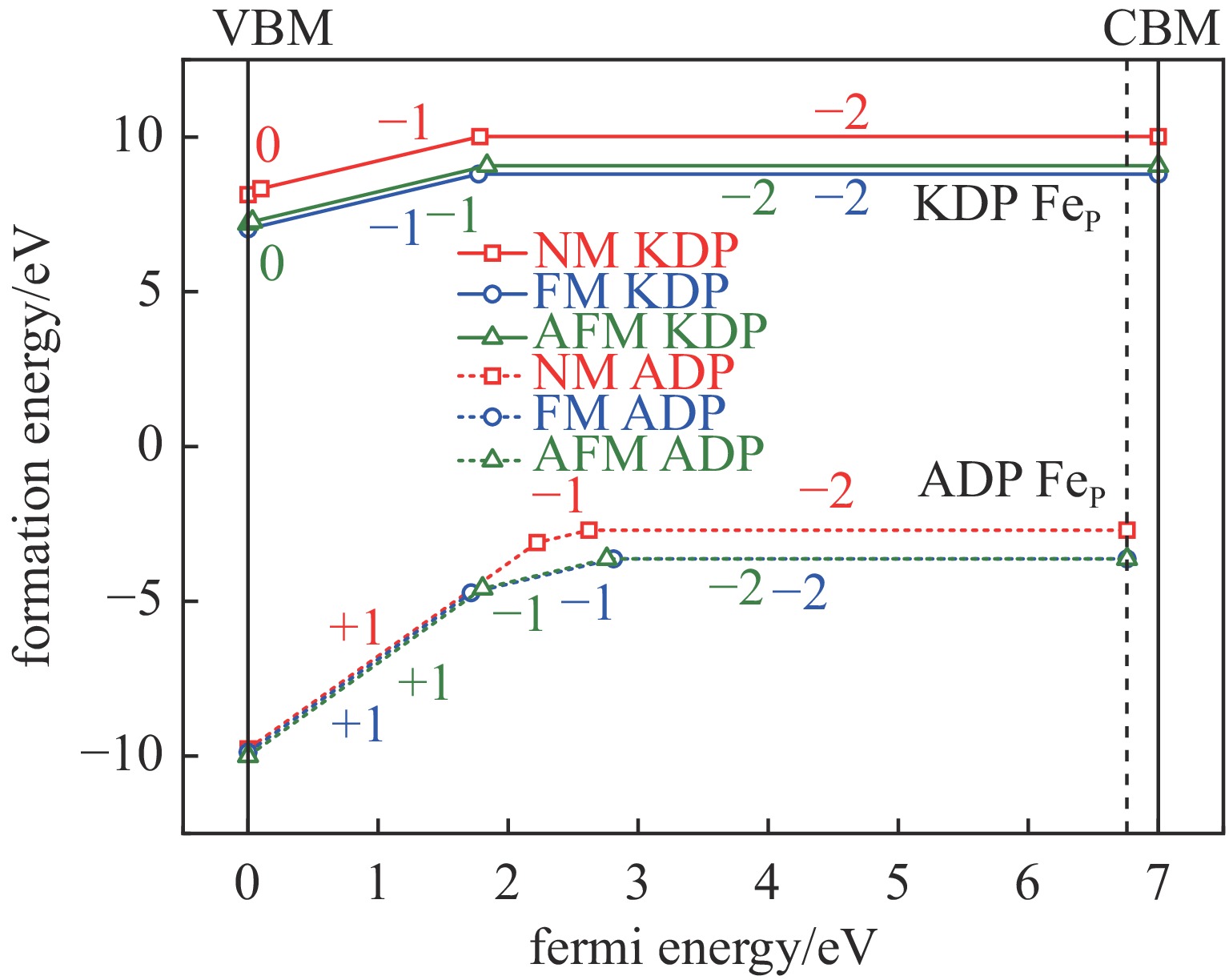
表  3  KDP和ADP晶体不同磁性条件下Fe−O键的键长变化

Table  3.  Fe−O bond lengths in KDP and ADP with different magnetic states

defects	bond length of Fe−O/nm
	KDP	ADP
pristine P-O	0.155	0.155
NM FeP+	0.162	0.160
NM FeP0	0.163	0.162
NM FeP−	0.166	0.165
NM FeP2−	0.170	0.169
FM FeP+	0.162	0.160
FM FeP0	0.163	0.162
FM FeP−	0.166	0.165
FM FeP2−	0.191	0.169
AFM FeP+	0.162	0.161
AFM FeP0	0.163	0.162
AFM FeP−	0.166	0.165
AFM FeP2−	0.170	0.169

下载: 导出CSV 

| 显示表格

为进一步探究晶体中缺陷中心捕获载流子引起的能量变化，研究了不同磁性状态的带电Fe_P缺陷的缺陷形成能随费米能级（E_F）的变化，如图3所示。图中CBM和VBM分别表示晶体的导带底和价带顶，KDP和ADP完美晶体的带隙值分别为7.00 eV和6.76 eV，费米能级在0～7.00 eV和0～6.76 eV之间变化。从图中可以看出，晶体初始状态费米能级在3.50 eV时，ADP晶体FM和AFM状态的Fe_P²⁻缺陷具有相对较低的缺陷形成能，比KDP晶体同磁性状态的Fe_P²⁻缺陷的形成能低约12 eV, 这说明Fe_P²⁻缺陷在ADP晶体中更易形成，此时Fe在晶体中为Fe³⁺。在KDP和ADP晶体中，不同磁性状态对应的缺陷的电荷转换能级有明显差异。例如，在KDP晶体中，NM状态下，Fe_P⁰缺陷具有最低的缺陷形成能，但其存在的范围很小，在E_F = 0.10 eV时即捕获一个电子转换成Fe_P⁻缺陷，随着缺陷浓度的增加，在E_F = 1.78 eV时继续捕获一个电子转换成稳定存在的Fe_P²⁻缺陷。在FM状态下，Fe_P⁻缺陷具有最低的缺陷形成能，在E_F = 1.77 eV时转换成稳定存在的Fe_P²⁻缺陷。AFM状态下缺陷的转换情况与NM相似，但体系的能量低于NM状态，表现出更稳定的结构特性。在ADP晶体中，NM状态下Fe_P⁺缺陷具有相对较低的缺陷形成能，且存在范围比KDP晶体中的Fe_P⁰缺陷大，随着缺陷浓度的增加，其在E_F = 2.23 eV时转换成Fe_P⁻缺陷，并在E_F = 2.62 eV转换成更稳定存在的Fe_P²⁻缺陷。与KDP晶体不同，ADP晶体的FM和AFM状态的缺陷的电荷态转换情况与其NM状态相似，缺陷经+1和−1电荷态转换成稳定存在的Fe_P²⁻缺陷，FM和AFM两个状态下体系的能量相差很小，约0.14 eV。在两种晶体中，FM和AFM状态都具有最低的缺陷形成能，三种磁性状态下体系能量差异很小，差值小于1.5 eV。但磁性状态改变了KDP晶体缺陷稳定存在的状态，而对ADP晶体的缺陷电荷态没有明显影响。虽然ADP晶体更容易受到Fe掺杂缺陷的影响，但结合表3中的Fe−O键变化情况分析，Fe原子掺杂带来的ADP晶体结构的变化比KDP晶体小，尤其是掺杂取代后稳定存在的Fe_P²⁻缺陷态。因此，能量上ADP晶体内更易产生Fe原子取代缺陷，且该缺陷对晶体结构的影响小于同条件下的KDP晶体，另外，电荷转换不受磁性条件变化的影响，所以在同样出现Fe原子掺杂点缺陷时，ADP晶体表现出相对较高的晶体结构稳定性和更高抵抗损伤的能力。

图  3  KDP和ADP晶体中不同磁性状态下Fe_P缺陷形成能随费米能级的变化

Figure  3.  Defect formation energies of the charged Fe_P defects in KDP and ADP as a function of Fermi energy with different magnetic states

下载: 全尺寸图片 幻灯片

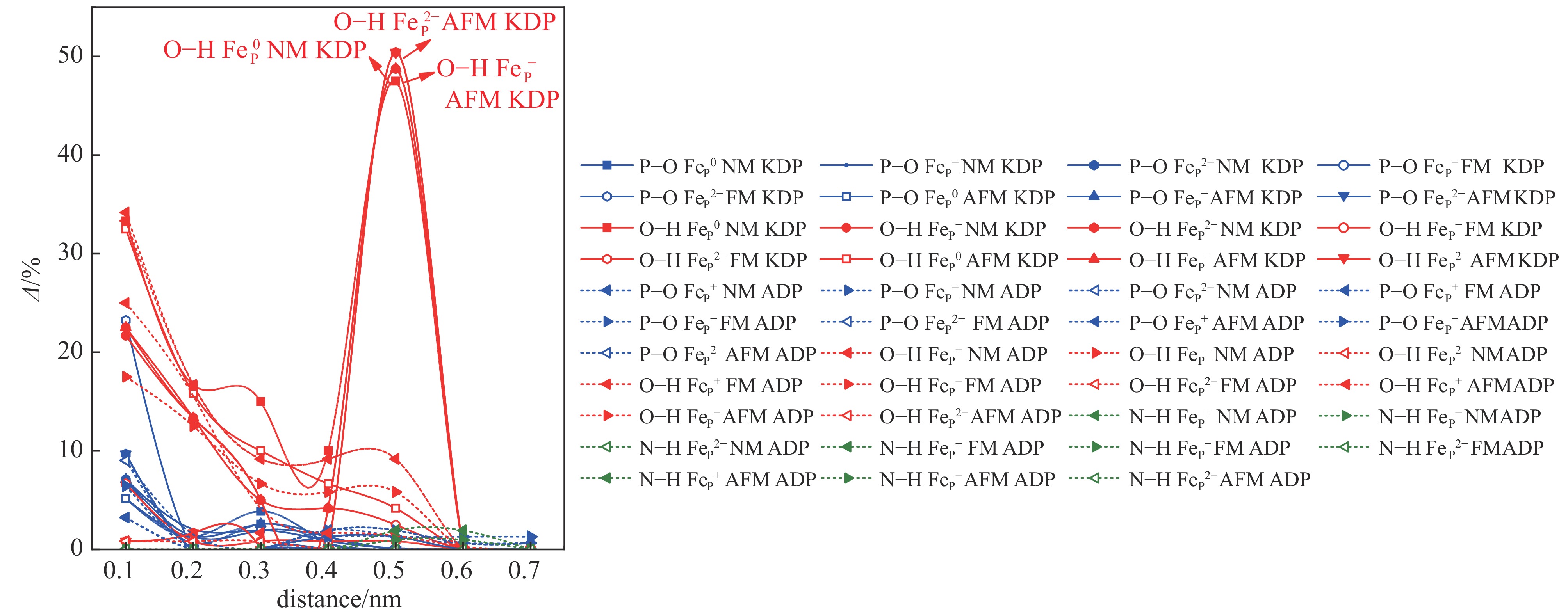
应力是影响光学损伤的一个重要因素，而缺陷是引起微观应力的主要来源。为研究掺杂Fe缺陷带来的微观应力变化，对不同磁性条件下Fe_P缺陷在KDP和ADP晶体中引起的微观应力变化情况进行了研究，结果如图4所示。从图中可以看出，距离缺陷处0.5 nm左右KDP晶体中O−H键产生相对较大的局域微观应力，这种微观应力主要表现在NM状态和AFM状态中，其中AFM状态下Fe_P²⁻缺陷的O−H键变化率最大，达到50.42%，其次是AFM状态下Fe_P⁻和NM状态下Fe_P⁰缺陷，O−H键的变化率分别为48.75%和47.08%。O−H键在近邻缺陷处的变化率也相对较大，这说明Fe取代P原子破坏了PO₄³⁻骨架结构之间的连接，使相互连接的O−H键发生相对较大的形变，造成晶体结构的不稳定，通过之前能量的计算可以判断O−H键的较大形变还不至于使其发生断裂。而在ADP晶体中，O−H键的变化率小于其在KDP晶体中的值，表现出相对更强的氢键相互牵连作用，使结构稳定性受Fe原子的影响较小。但微观应力具有传播性，随着缺陷浓度的逐渐增大，微观应力不断增大、累积，会对整个晶体结构造成破坏，其影响不容忽视。与此同时，P−O键的变化率大部分不超过20%，N−H键的变化率更小，不超过10%，证明Fe_P缺陷对P−O和N−H键微观应力的影响较小。与本征缺陷造成的微观应力的影响相比，掺杂离子对晶体结构的影响较小，在一定程度上说明掺杂离子对晶体结构的影响不足以使晶体的抗损伤能力有较大破坏，其对晶体的影响可能体现在电子及光学性质方面。

图  4  不同磁性状态下KDP和ADP晶体中Fe_P缺陷的各化学键引起的微观应力变化

Figure  4.  Micro-structural stress induced by various chemical bonds of Fe_P defect with different magnetic states in KDP and ADP crystals

下载: 全尺寸图片 幻灯片

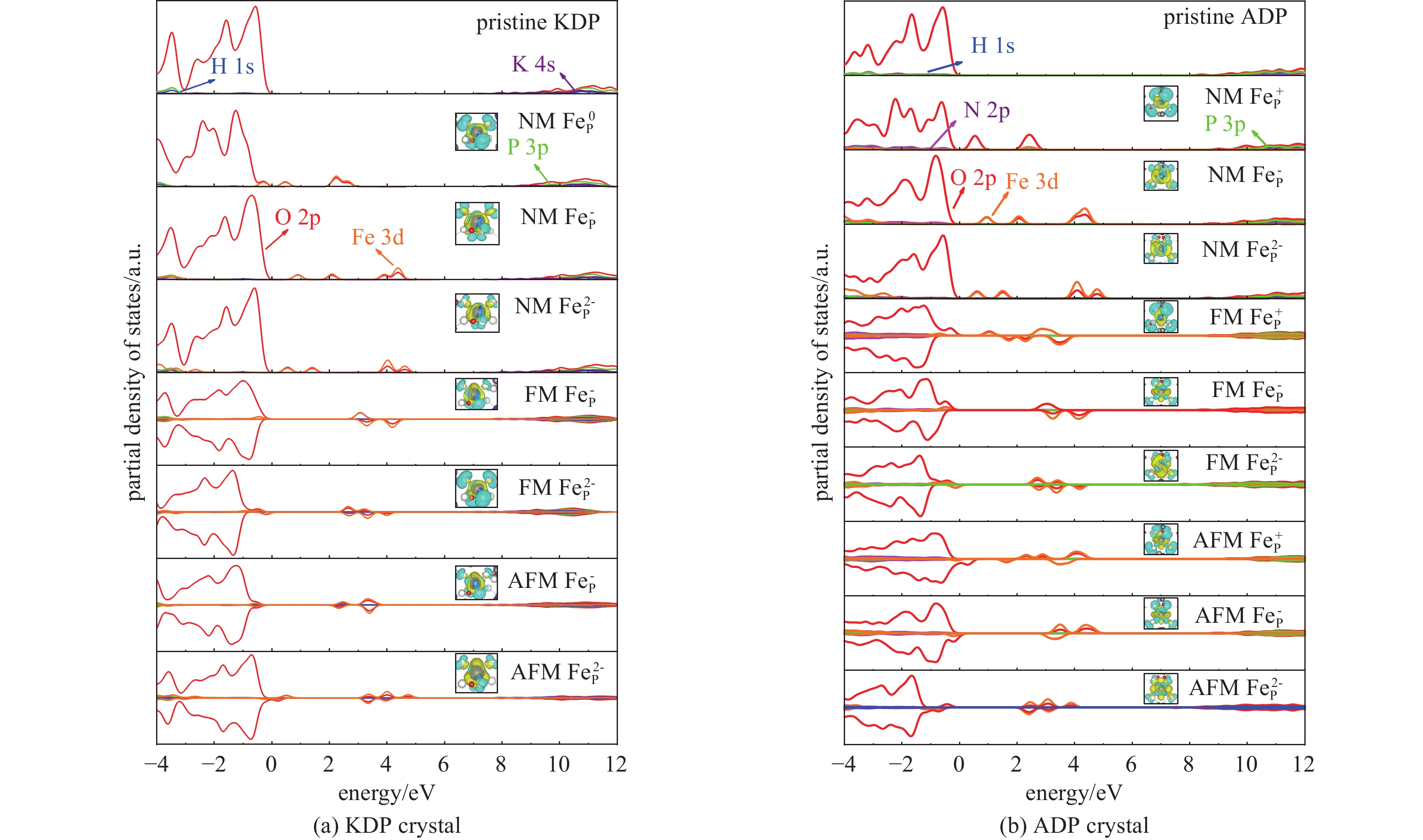
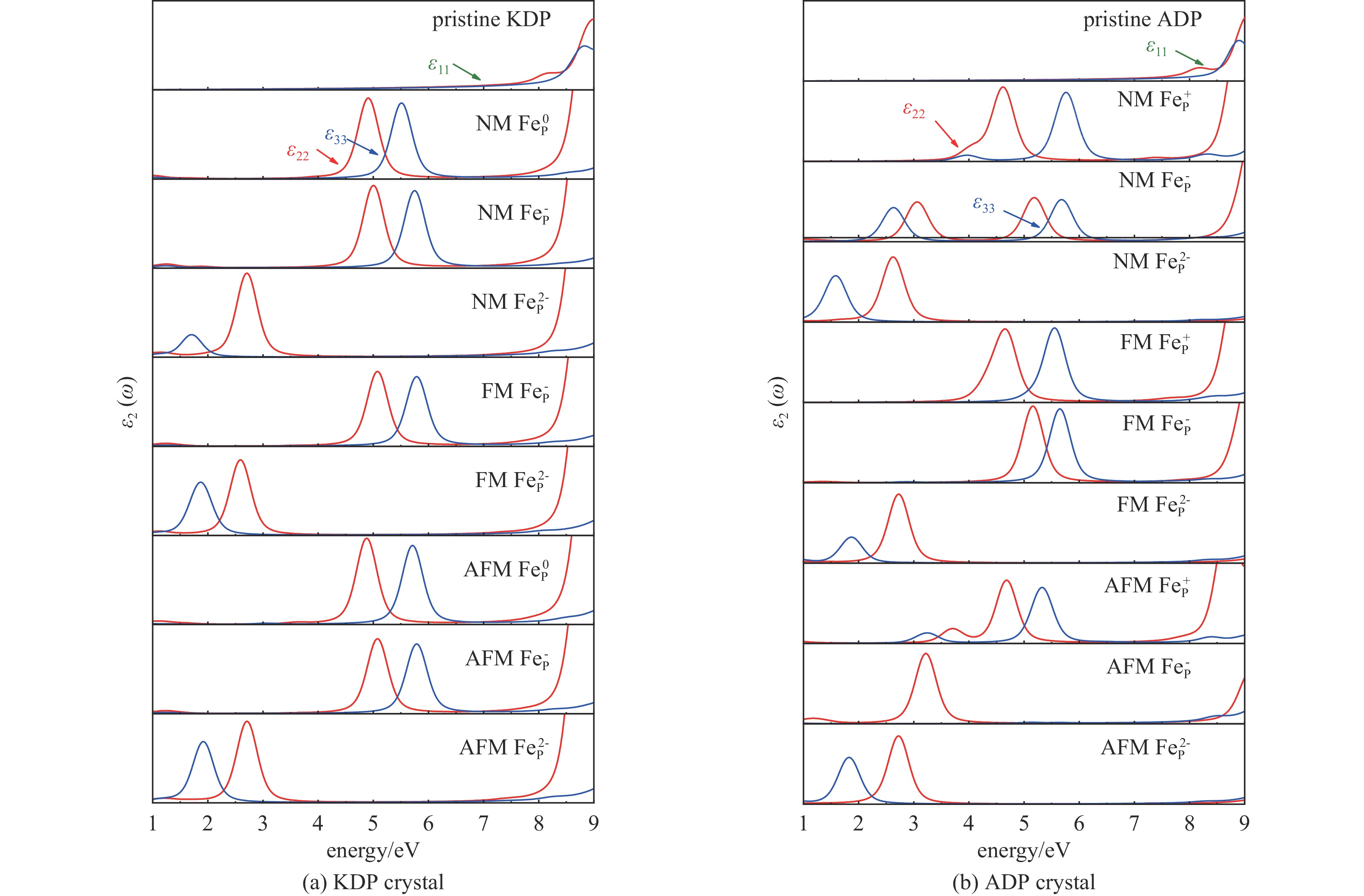
为证实这一推测，计算了KDP和ADP晶体中Fe_P缺陷不同自旋极化状态下的电子结构及其光学性质^[33-37]，分态密度如图5所示，图5中插图为电荷差分密度图，黄色和蓝色分别表示电子的累积和消耗，介电函数虚部ε₂（ω）如图6所示。从图5可以看出，顺磁（NM）状态下KDP晶体中Fe_P⁰缺陷在近价带顶引入孤立的未占据的杂质能级，主要由O 2p电子态和Fe 3d电子态共同作用。当缺陷捕获一个电子形成Fe_P⁻缺陷，杂质态向导带底的方向移动约1.5 eV，杂质态仍由O 2p电子态和Fe 3d电子态贡献。以上两种缺陷态均在5 eV（248 nm）和5.8 eV（213.8 nm）位置引入沿ε₂₂方向和ε₃₃方向的吸收峰，吸收沿晶体bc方向分布，如图6（a）所示。当缺陷继续捕获电子形成稳定的Fe_P²⁻缺陷时，杂质态移至价带顶约0.5、1.5和4 eV处，引起位于1.5 eV（826.7 nm）及2.8 eV（442.9 nm）的吸收峰，分别沿c轴和b轴方向分布。缺陷态的电子得失主要来源于近邻O与Fe之间的电子转移。在铁磁（FM）状态下，Fe_P⁻缺陷引入一个自旋向上的空杂质态，位于3 eV处，两个自旋向下的空杂质态，位于3.3和4.2 eV处。O 2p和Fe 3d电子态之间的电子跃迁引起在5 eV（248 nm）和5.8 eV（213.8 nm）位置的沿着ε₂₂方向和ε₃₃方向的吸收峰，吸收沿晶体的bc方向分布，如图6（a）所示，这种光吸收情况与NM状态下相同。当Fe_P⁻缺陷捕获电子形成稳定的Fe_P²⁻缺陷时，电子占据的杂质态部分移至价带顶中，其余占据的杂质态分别在2.6、3.2和4.0 eV处，杂质态同样由Fe与O原子的杂化贡献，与NM状态相同，杂质态引入1.5 eV（826.7 nm）及2.8 eV（442.9 nm）的吸收峰，分别沿c轴和b轴方向分布，但在c轴方向的吸收峰强度明显高于NM状态下c轴的吸收峰强度。在反铁磁（AFM）状态下，Fe_P⁻的缺陷态位于2.8 eV和3.8 eV，Fe_P⁻缺陷和Fe_P²⁻缺陷表现出与FM状态下相似的电子性质，Fe_P²⁻缺陷的缺陷态分别占据3.8、4.0和4.6 eV，均来自O 2p和Fe 3d电子态，O与Fe之间的杂化使晶体出现了与NM状态下类似的明显光吸收现象。以上状态中出现的较强的光学吸收将会明显影响晶体抗光损伤的能力，在强光辐照条件下极易出现损伤，严重影响晶体的性能。

图  5  KDP和ADP晶体中不同磁性条件下Fe_P 缺陷电荷态的分态密度图，插图为各状态下缺陷的差分电荷密度图

Figure  5.  Partial density of states of KDP and ADP crystals with charged Fe_P defects in different magnetic states, and the insets are electronic charge differences of charged Fe_P defects with different magnetic states

下载: 全尺寸图片 幻灯片

图  6  KDP和ADP晶体中不同磁性条件下Fe_P缺陷电荷态的介电函数虚部ε₂ (ω)

Figure  6.  Imaginary part of the dielectric function ε₂ (ω) of charged Fe_P defects with different magnetic states in KDP and ADP crystals

下载: 全尺寸图片 幻灯片

在ADP晶体中，Fe原子掺杂缺陷表现出与KDP晶体相似的电子与光学性质的影响。在顺磁（NM）状态下，Fe_P⁺缺陷在价带顶0.5 eV及2.5 eV左右处引入由O 2p和Fe 3d电子态贡献的缺陷态，O原子与Fe原子的电子跃迁使4.5 eV（275.6 nm）及5.8 eV（213.8 nm）处出现分别沿ε₂₂和ε₃₃方向分布的光学吸收峰。当缺陷捕获两个电子形成Fe_P⁻缺陷时，4.3 eV处新引入一个同样由O 2p和Fe 3d电子态贡献的杂质态。从图6（b）可以看出，杂质态引起位于3.2 eV（387.5 nm）和5.5 eV（225.5 nm）沿ε₂₂方向分布的光学吸收峰，以及位于2.5 eV（486 nm）和5.8 eV（213.8 nm）沿ε₃₃方向分布的光学吸收峰。缺陷继续捕获电子形成更稳定的Fe_P²⁻缺陷，4.8 eV处新引入一个由O 2p和Fe 3d电子态贡献的杂质态。与KDP晶体中的NM状态类似，杂质态引入位于1.5 eV（826.7 nm）及2.8 eV（442.9 nm）的吸收峰，分别沿c轴和b轴方向分布。在铁磁（FM）状态下，Fe_P⁺缺陷引入自旋向上和自旋向下的空的缺陷态，同样来源于O 2p和Fe 3d电子态，并分别在4.5 eV（275.6 nm）和5.5 eV（225.5 nm）处引入光学吸收峰。当缺陷捕获两个电子，从图5（b）可以看出，被捕获的电子分布在缺陷中心及近邻O原子周围，缺陷态同样引入类似于Fe_P⁺缺陷的光学吸收峰。当缺陷继续捕获电子形成更稳定的Fe_P²⁻缺陷时，两对自旋平行的电子占据2.8 eV和3.2 eV的杂质态，一个自旋向下的电子占据4.1 eV的杂质态，缺陷态引入了与NM状态下相同的光学吸收峰。在反铁磁（AFM）的状态下，Fe_P⁺缺陷不断捕获电子最终形成稳定存在的Fe_P²⁻缺陷，随着缺陷捕获电子数量的增加，缺陷态的位置不断向价带顶的方向移动，Fe 3d和O 2p电子态之间的电荷转移引起的光学吸收峰不断蓝移，在晶体中形成沿bc方向分布的较大范围的光学吸收峰。

综上所述，KDP和ADP晶体中的Fe原子掺杂，在不同磁性状态下引起的缺陷态的位置略有不同，引起光学吸收峰的位置也有所差异，但缺陷态的主要来源均为O 2p和Fe 3d电子态，电子跃迁引起光学吸收的变化，致使晶体沿b和c方向200～300 nm范围出现明显的光学吸收峰，严重影响晶体的光学性能，这与文献中报道的实验值相近^[9]。与KDP晶体相比，ADP晶体更易受到掺杂Fe元素的影响，表现出明显的光学吸收性质，晶体中的氢键不足以制约光学吸收在晶体中的传播，抵抗光损伤的能力下降。模拟的结果说明，即使Fe原子掺杂的ADP晶体的抗损伤能力下降，其在掺杂缺陷的情况下反映出的抵抗激光损伤的能力也高于同条件下Fe原子掺杂的KDP晶体。但Fe³⁺等杂质离子对晶体损伤的影响不容忽视，尤其是Fe³⁺杂质在晶体中与本征缺陷复合成团簇缺陷时，其对晶体结构和性质的影响也主要以Fe³⁺的影响为主，因此在生长和加工过程中应严格控制杂质离子的含量。

3.   结　论

本文基于第一性原理方法，研究了掺杂Fe点缺陷对KDP和ADP晶体结构和性能的影响，分析了其对晶体光损伤的影响及机理。从结构和能量的角度分析了KDP和ADP晶体中掺杂Fe点缺陷引起的结构变化和稳定性。通过理论模拟发现Fe原子进入晶体取代P原子形成FeO₄基团，没有对骨架结构造成坍塌性破坏；Fe的磁性状态几乎对两晶体的结构不产生影响；与KDP晶体相比，Fe原子掺杂更易在ADP晶体中形成。 KDP晶体中距离缺陷处0.5 nm左右的O−H键具有相对较大的局域微观应力，缺陷破坏了PO₄³⁻骨架结构之间的连接，使相互连接的O−H键发生相对较大的形变，造成晶体结构的不稳定。在ADP晶体中，O−H键的变化率小于其在KDP晶体中的值，表现出相对更强的氢键的相互牵连作用，结构稳定性相对更强。尽管ADP晶体中存在大量的氢键可以牵制晶体中缺陷带来的结构变化，但掺杂缺陷对光学性质的影响却依旧存在。 KDP和ADP晶体不同磁性状态的电子性质及光吸收性质表现形式不同，但两者均引入由Fe 3d和O 2p电子态共同作用的缺陷能级，电子的跃迁引起了200～300 nm范围明显的光学吸收峰，致使晶体的光学吸收性能明显降低，使其抵抗损伤的能力下降，从而影响晶体的损伤阈值。在晶体的实际应用中，应控制晶体中杂质缺陷的含量，尽量降低杂质离子对晶体损伤阈值的影响。