High-resolution reconstruction of the ablative RT instability flow field via convolutional neural networks
-
Abstract:
High-resolution flow field data has important applications in meteorology, aerospace engineering, high-energy physics and other fields. Experiments and numerical simulations are two main ways to obtain high-resolution flow field data, while the high experiment cost and computing resources for simulation hinder the specific analysis of flow field evolution. With the development of deep learning technology, convolutional neural networks are used to achieve high-resolution reconstruction of the flow field. In this paper, an ordinary convolutional neural network and a multi-time-path convolutional neural network are established for the ablative Rayleigh-Taylor instability. These two methods can reconstruct the high-resolution flow field in just a few seconds, and further greatly enrich the application of high-resolution reconstruction technology in fluid instability. Compared with the ordinary convolutional neural network, the multi-time-path convolutional neural network model has smaller error and can restore more details of the flow field. The influence of low-resolution flow field data obtained by the two pooling methods on the convolutional neural networks model is also discussed.
摘要:高分辨率流场数据在气象学、航空航天工程、高能物理等领域有着重要的应用价值。实验和数值模拟是两种获取高分辨率流场数据的主要途径。但是高昂的实验成本和仿真计算资源阻碍了研究者对流场演化的具体分析。随着深度学习技术的发展,卷积神经网络被用来实现流场的高分辨率重建。针对烧蚀瑞利-泰勒不稳定性流场重建提出了普通卷积神经网络模型和多重时间路径卷积神经网络模型。这两个模型可以在很短的时间内对流场进行高分辨率重建,极大地丰富了高分辨率重建技术在流体不稳定性研究中的应用。与普通卷积神经网络相比,多重时间路径卷积神经网络模型的误差较小,可以还原流场的更多细节。此外,还讨论了用于获取低分辨率流场的不同池化方法对卷积神经网络模型性能的影响。
-
关键词:
- 卷积神经网络 /
- 烧蚀瑞利-泰勒不稳定性 /
- 高分辨率重建 /
- 多重时间路径 /
- 池化
-
High-resolution flow field data play an important role in fluid mechanics, fluid dynamics research, engineering design and technological innovations. Accurate acquisition and analysis of high-resolution flow field data is of great significance for understanding flow phenomena. There are two main ways to obtain high-resolution flow field data, one is experimental measurements, such as Particle Image Velocimetry (PIV)[1], the other is Computational Fluid Dynamics (CFD)[2], such as Direct Numerical Simulation (DNS)[3-5]. However, obtaining high-resolution flow field data through experiments or CFD is either costly or time-consuming, thus new methods need to be developed.
Artificial intelligence technology has been booming unprecedentedly nowadays[6]. As the main method of artificial intelligence, Convolutional Neural Networks (CNN)[7] has been widely used in various fields and promoted many innovations and progress. CNN is a deep learning model inspired by the biological vision system. The development of CNN has experienced many milestones. The earliest CNN model can be traced back to the 1990s, such as LeNet[8] proposed by LeCun for handwritten digit recognition. In the 2012 ImageNet Large-Scale Visual Recognition Challenge, the emergence of the AlexNet[9] model has greatly promoted the development of CNN, which uses a deeper networks structure and a large amount of image data for training, and achieved breakthrough results. Since then, various improved CNN models have emerged, such as VGGNet[10], GoogLeNet[11], ResNet[12], etc., which have achieved excellent performance in different computer vision tasks.
The vigorous development of CNN has been spread to various fields, including fluid mechanics. Especially in recent years, fluid mechanics has been closely combined with CNN. In 2018, Jin et al designed a fused CNN model[13]. Through this model, the velocity field around the cylinder can be predicted only according to the pressure fluctuation on the cylinder. This model has good performance under different Reynolds numbers. In 2019, Sekar et al first used CNN to extract the geometric features of the airfoil[14], and to predict the flow field around the airfoil through the fully connected layer with the help of other state information. In the direction of high-resolution reconstruction of the flow field, Fukaimi et al proposed a hybrid Down sampled Skip-Connection Multi-Scale model to reconstruct the flow field[15] in 2019. In this model, only dozens of training samples are used to produce a good performance. At the same year, Deng et al constructed two models based on generative adversarial networks to enhance the spatial resolution of the complex wake behind two side-by-side cylinders[16]. In 2020, Liu et al developed the multi-time-path CNN model for high-resolution reconstruction of turbulence[17]. In 2021, Zhou et al used the geometric parameters of the coarse velocity field and the pore structure as the input of the CNN model to achieve super-resolution reconstruction of the pore flow field in porous media[18]. In 2022, Jagodinski et al designed a three-dimensional CNN model to identify significant structures related to ejection events in wall-bounded turbulent flows[19].
The ablative Rayleigh–Taylor instability (ARTI)[20] flow field data is mainly obtained by numerical simulations and experiments. At present, high-precision simulation requires fine meshing, however, it is costly and time-consuming. Low-precision simulation takes a short time, but it cannot describe the physical characteristics of the flow field in detail. Therefore, we need to develop a new method that can obtain high-precision ablation Rayleigh-Taylor instability flow field data at a relatively small computational cost. In this study, two different CNN models are given out to perform the high-resolution reconstruction. These two models can quickly transform low-resolution data into high-resolution data, which allows us to obtain high-resolution ARTI flow field data rapidly.
1. Methods
1.1 ARTI and DNS
The Rayleigh–Taylor instability (RTI) occurs at the perturbation interface of two fluids with different densities, where the light fluid accelerates or supports the heavy fluid[21]. In inertial confinement fusion (ICF), RTI can break the symmetry of implosions by dismantling the integrity of the spherical ablator-fuel shell. Therefore, it is crucial to predict the growth of RTI to improve the success probability of ICF. The inclusion of thermal conduction influences leads to a different hydrodynamic instability, which is then identified as ARTI, occurring between the internal and external layers during the implosion phase of ICF[22].
The control equations of the ARTI over a constantly accelerating 2D reference frame are as follows
∂tρ=−∂x(ρu)−∂y(ρv), (1) ∂t(ρu)=−∂x(ρu2+p)−∂y(ρuv)+ρg, (2) ∂t(ρv)=−∂x(ρuv)−∂y(ρv2+p), (3) ∂t(ρe)=−∂x[(ρe+p)u]−∂y[(ρe+p)v]+∂x(κ∂xT)+∂y(κ∂yT)+ρug, (4) where
ρ , u, v and T represent density, x-axis velocity component, y-axis velocity component and temperature, respectively. g is acceleration,p=ΓρT is the pressure, ande=CvρT+ρv22 is the total energy, whereCv=Γ/(γh−1) is the constant-volume specific heat. For CH material,γh=5/3 andΓ=57.51cm2/(μs2⋅MK) .κ=κSHf(T)h is the coefficient of thermal conductivity, whereκSH∝T5/2 is the classical electron thermal conductivity coefficient.f(T)=1+bT+c/T3/2 is the preheating function, andh=1/[1+B⋅ln(TmaxT0)] because there is a large temperature gradient near the critical surface,T0 andTmax are the initial electron temperature and the maximum electron temperature, respectively, in the corona region, and B is an adjustable parameter, usuallyB=1 . For the strong preheat case discussed in this paper, we set h=1, b=8.6, c=1.6.The data used in this work are derived from the DNS of ARTI in Ref.[4], and the Euler code which has been usually applicated in high energy density physics is used in our study. Before the formal training of the CNN model, we process the original DNS data through region selection, dislocation stitching, pooling and other processes to obtain the sample data. In this paper, both maximum pooling and average pooling are used to implement down-sampling.
1.2 Two CNN models
In this paper, the application of ordinary CNN model and multi-time-path CNN model are discussed, and the results are also compared with those of the BiCubic interpolation method[23].
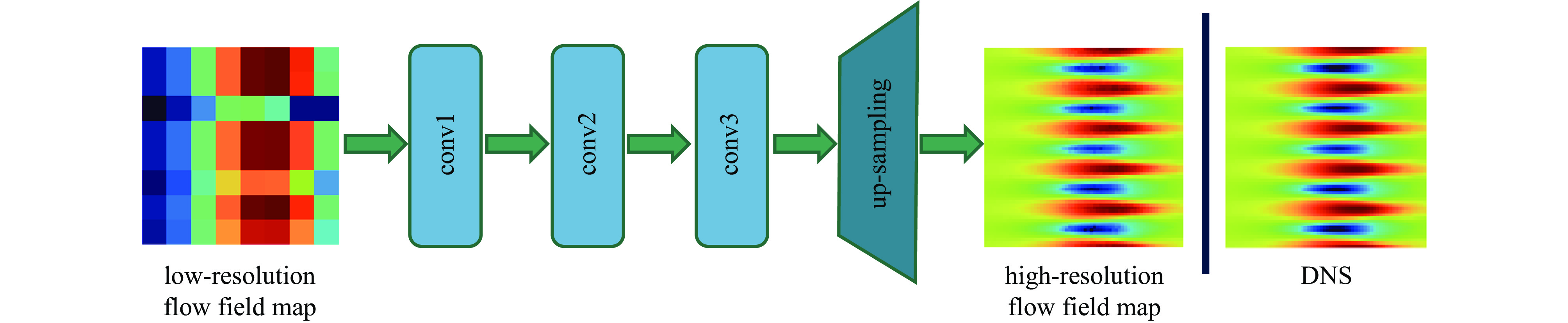
The ordinary CNN model consists of three convolution layers and an up-sampling layer, as shown in Fig.1. The input of the model is the low-resolution flow field data and the output is the high-resolution flow field data at the same time. The role of the convolution layer is to extract the characteristics of the flow field data. The size of the convolution kernel is
3×3 . The function of the up-sampling layer is to integrate and enlarge the feature maps obtained by convolution operation, so as to achieve high-resolution reconstruction. The PixelShuffle up-sampling method[24] is adopted to transform the feature map with the input size of(r2×C,H,W) into the flow field map with the input size of(C,r×H,r×W) by pixel recombination of the low-resolution feature map,where r is the reconstruction magnification, C is the number of channels, H is the height of the feature map, W is the width of the feature map.The second model is a multi-time-path CNN. The schematic diagram of the model is shown in Fig.2.
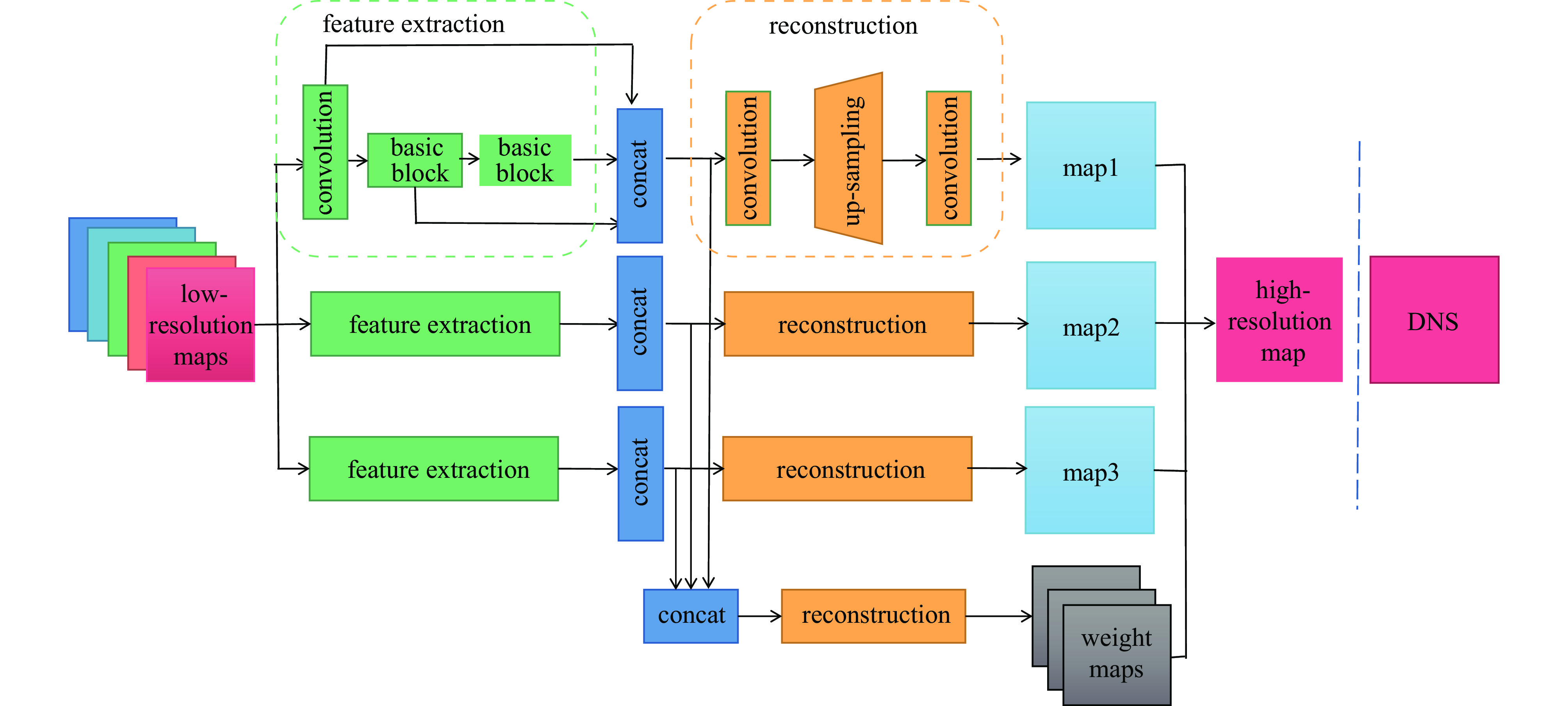
The input of the multi-time-path CNN is the low-resolution flow field data of the five moments at
t−2Δt ,t−Δt , t,t+Δt ,t+2Δt respectively and the output is the high-resolution flow field data of the moment t. The model includes four paths, three of which are time paths and the other is the weight path. The time paths include the backward time path, central time path and forward time path. The input of each time path is the low-resolution flow field data at three consecutive moments. The input of the backward time path is the flow field data at three moments oft−2Δt ,t−Δt , t. The input of the central time path is the flow field data at three moments oft−Δt , t,t+Δt . The input of the forward time path is the flow field data at three moments of t,t+Δt ,t+2Δt . Therefore, a set of input data of the model contains low-resolution flow field data at five moments. The structures of all the time paths are the same, including feature extraction module and reconstruction module. The feature extraction module consists of two basic blocks, each of which is an enhanced multi-scale residual block[25], and a jump connection method is used on each time path to avoid the loss of features caused by convolution operations. In the weight path, the input is the feature maps extracted by the feature extraction module of the three time paths, and the output is three weight maps. The summation of the products of the obtained weight map and the reconstructed flow field map obtained by the three time paths will finally give the high-resolution flow field map at the moment t. In other words, the final high-resolution flow field data is actually the weighted average of the high-resolution flow field data obtained by the three time paths.Compared with the ordinary CNN, multi-time-path CNN has more input data and more complex networks structure, thus the expected results should also be better than those of the ordinary CNN. It is worth mentioning that the multi-time-path CNN takes the time series as the model input, combines the timing of the flow field changing with time, and has the superiority that the ordinary CNN cannot achieve.
1.3 Model training
After a series of data processing, we randomly divided
2000 samples into 80% training set (1600 samples) and 20% test set (400 samples). Taking a magnification of 4 as an example, the input size of our ordinary CNN model is [C, 16, 16], and the input size of the multi-time-path CNN is [3, C * 3, 16, 16]. Because the multi-time-path CNN has three paths, there is an additional dimension on the input scale. Each path of the multi-time-path CNN contains data of three moments, thus, the number of channels is C * 3. The last two dimensions represent the height and width of the feature map. We set the batch size to be 32 and Epoch to be 2000.Before putting into training, the input data should be normalized, which will make the model converge faster. We select activation function as the ReLU function, which is often used in neural networks. Because our super-resolution reconstruction task is actually a regression task, we cannot use the activation function in the last convolution layer. For weight initialization, we also use the corresponding initialization method of ReLU function.
The loss function in the above two models is written as
L=∑Ni=1(Hi−Pi)2N, (5) where L is also called as Mean Square Error (MSE), N is the number of data point, H, P are the real value and the predicted value of the point, respectively.
All the models in this paper are in Python, which mainly depends on PyTorch to realize the construction of CNN model. As for gradient update, Adam[26] (Adaptive Moment Estimation) optimization algorithm is used to adaptively adjust the parameters in the neural networks, which can converge to the optimal solution quickly. In the parameter setting of Adam, we choose the learning rate 0.0001. The training process of the model involves iterating through 2000 epochs. The ordinary CNN takes 4 h and 2 min, and the multi-time-path CNN takes 4 h and 23 min. The structure of the multi-time-path CNN is more complex and has more parameters than the ordinary CNN, thus requiring a slightly longer computation time. After the model training is completed, the high-resolution reconstruction task can be achieved in a few seconds.
2. Results and analysis
The DNS data used here are ARTI flow field data with a disturbance wavelength
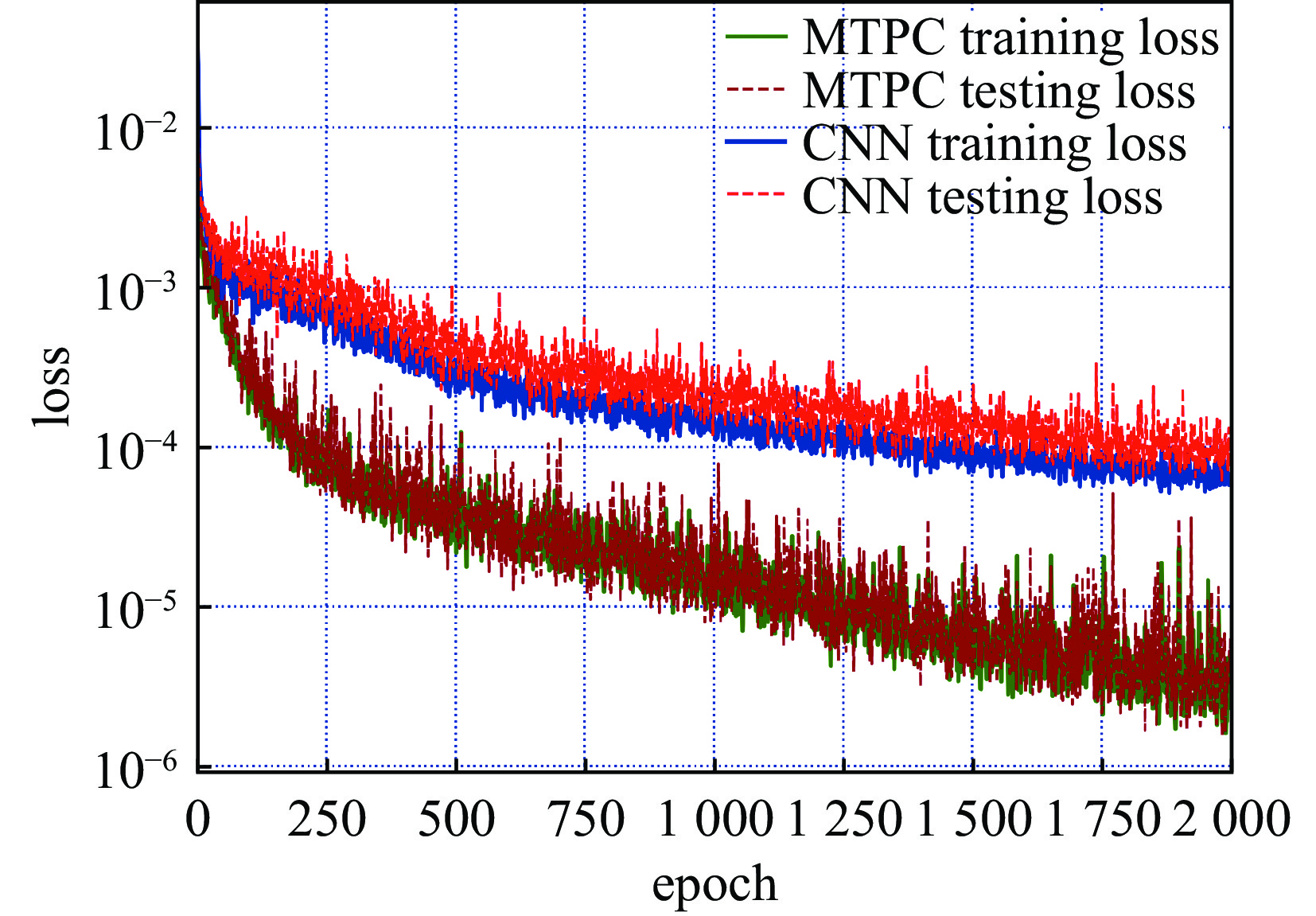
Ld=12μm . Firstly, the velocity field is reconstructed by using the data of the two channels in the x, y directions as the input of the model. The training error and test set error of the ordinary CNN model and the multiple CNN model are shown in Fig.3.In Fig.3, CNN represents the ordinary CNN, MTPC represents the multi-time-path CNN, training loss refers to the training set error, and testing loss refers to the test set error. Compared with the ordinary CNN, the error of the multi-time-path CNN is smaller, reduced by nearly 10 times. It can be said that the multi-time-path CNN has better reconstruction performance than the ordinary CNN.
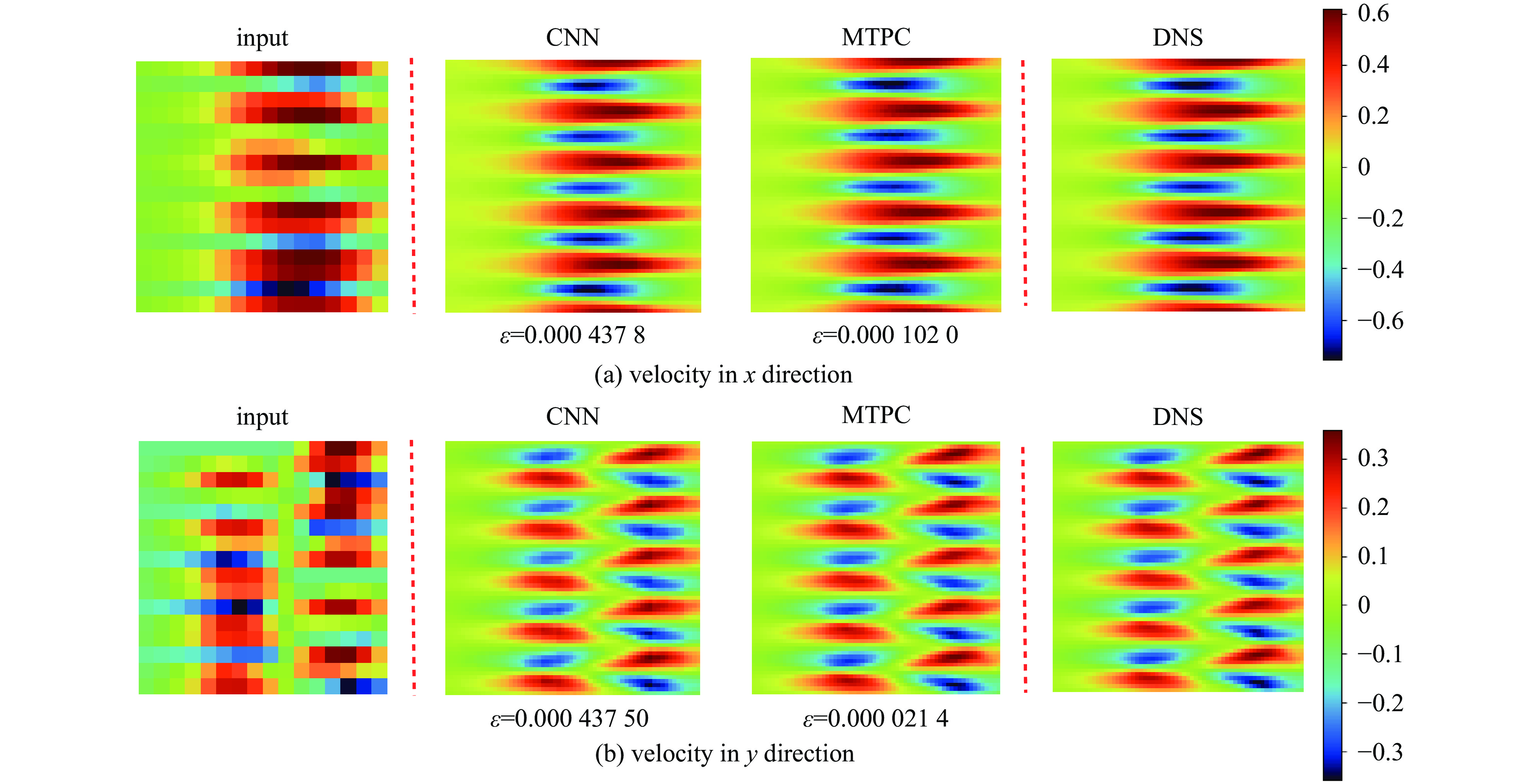
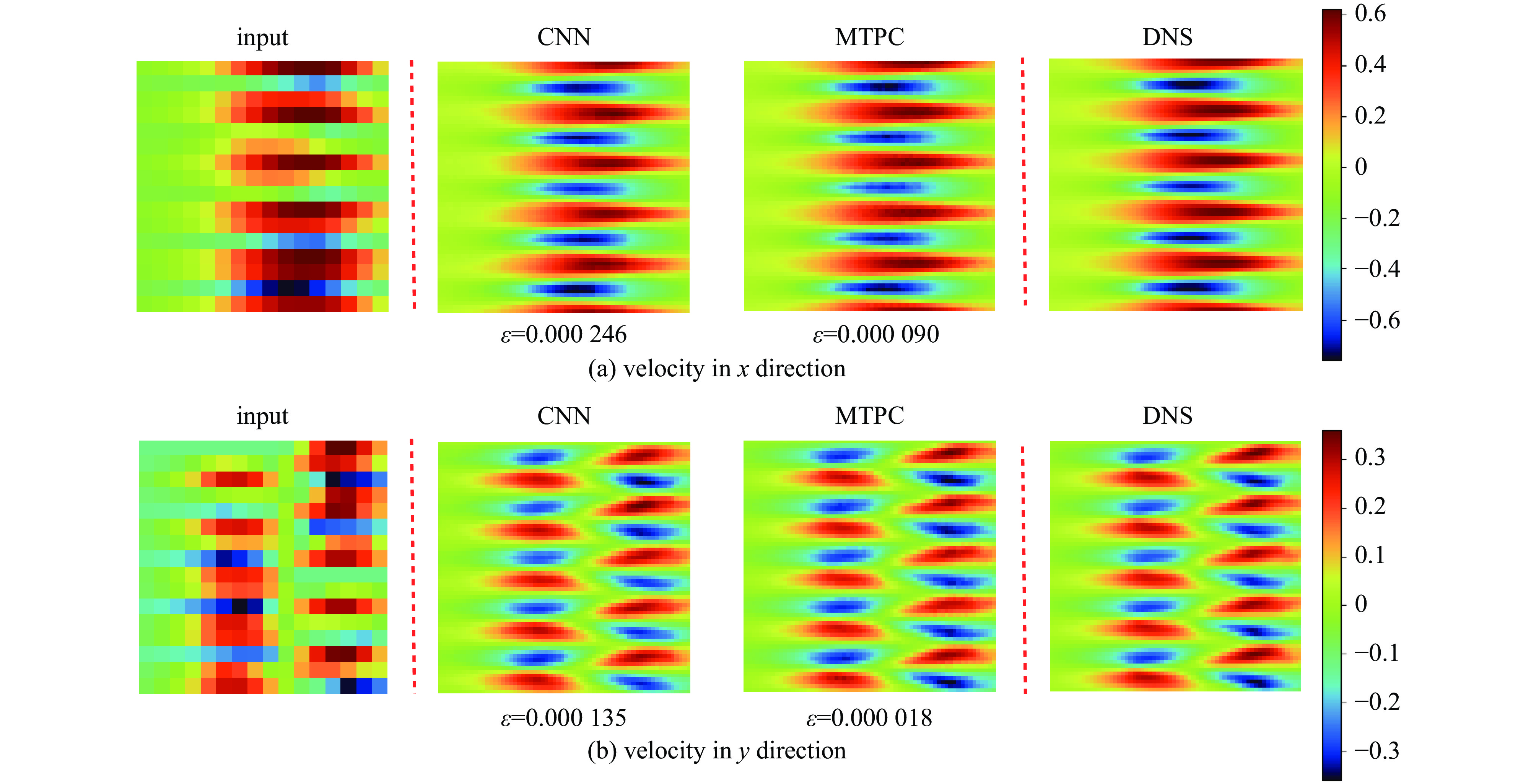
To more clearly show the superiority of the multi-time-path CNN, we compare the reconstructed results of the two models. All the data shown in Fig.4 and Fig.5 come from the same flow field,which are the flow field velocity data of the same position at the same time.
Fig.4 is the comparison of the reconstruction results when the input is the flow field velocity data in x and y directions after average pooling. Fig.5 is the comparison of the reconstruction results when the input is the flow field velocity data in two directions after maximum pooling. The reconstruction magnification r of the two figures is 4, and the
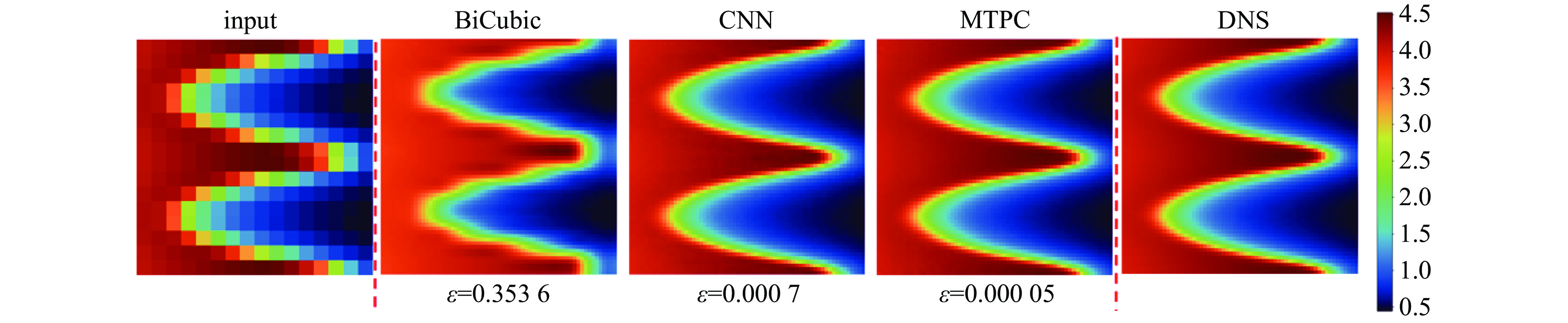
ε in the figure is the MSE. It can be clearly seen that the MSE of the multi-time-path CNN is much smaller than that of the ordinary CNN for both the average pooling case and the maximum pooling case. To show that the performance of the multi-time-path CNN is better than that of the ordinary CNN, we also compare the reconstruction results of models with magnification r= 8. The results show that even when the magnification r is 8, the error of the multi-time-path CNN is still much smaller than that of the ordinary CNN. Compared with the case of magnification r being 4, the error increases when the magnification r is 8, which is also in line with expectations: as the magnification increases, the amount of input data decreases, and the error of the model should also increase. Comparing the results of average pooling and maximum pooling, average pooling will lead to smooth prediction results but reduce accuracy, while maximum pooling can retain more details and help to improve prediction accuracy, but the results are not as smooth as average pooling.Furthermore, the density of the flow field is also used for training the model as a separate input. To demonstrate the universality of the model, we analyze the flow field density data of four cases (r=4). The first case is the density data of the weak nonlinear stage with ablation (disturbance wavelength=12 μm), as shown in Fig.6.
BiCubic in Fig.6 denotes the results of the BiCubic interpolation reconstruction method, and the BiCubic interpolation method is widely used in image processing. The prediction results of the BiCubic interpolation method exhibit excessive smoothness, resulting in the loss of numerous detailed characteristics within the flow field. It can be clearly seen from Fig.6 that the performance of both ordinary CNN and multi-time-path CNN in high-resolution reconstruction of flow field data is far superior to that of BiCubic interpolation method. The multi-time-path CNN consistently demonstrates superior performance compared to the ordinary CNN, effectively recovering more flow field details with a lower error.
Fig.7 is the classical linear flow field density data (disturbance wavelength=12 μm), and Fig.8 is the density data of the nonlinear stage with ablation (disturbance wavelength=12 μm). In addition, we also discuss the flow field with the disturbance wavelength of 30 μm, as shown in Fig.9.
In these cases, the prediction error of the multi-time-path CNN is generally at the order of 10−5, while the error of the ordinary CNN is at the order of 10−4. Both of these errors are significantly lower than that of the the BiCubic interpolation method. It is shown by these cases that the multi-time-path CNN still exhibits excellent performance in the face of different flow parameters, different stages and different flow field data.
For the velocity component input case and the density component input case, the error of reconstructing the flow field based on multi-time-path CNN is low enough, and the performance is sufficiently good. This also fully demonstrates the feasibility of combining machine learning with fluid mechanics. The methods used in this paper can also be applied to other flow field data. Given a sufficient amount of flow field data, a corresponding high-resolution reconstruction model can be trained.
3. Conclusion
We have built an ordinary CNN and a multi-time-path CNN to achieve high-resolution reconstruction of the low-resolution ablation Rayleigh-Taylor instability flow field. Compared with the ordinary CNN, the multi-time-path CNN shows better performance and smaller error. In terms of the acquisition of input data, we first pooled the existing high-precision DNS data of our research group to obtain low-resolution flow field data, and then we performed dislocation splicing on the data to obtain training sample data. The influence of input data obtained by two pooling methods on model training is compared. The prediction results of the average pooling model are smoother, and the accuracy of the maximum pooling model is slightly higher. Different cases are discussed in this paper, and it is found that the multi-time-path CNN model still maintains excellent performance in different flow fields. Once the CNN model is trained, the high-resolution reconstruction task can be completed in just a few seconds. The introduction of these two models has enriched the application of CNN in fluid instability. With the development of computer technology, the training speed of CNN model will be faster and faster. We can construct more complex models to make the reconstruction accuracy higher and higher.
-
-
[1] Adrian R J. Twenty years of particle image velocimetry[J]. Exp Fluids, 2005, 39: 159-169. doi: 10.1007/s00348-005-0991-7 [2] Yan Chao, Yu Jian, Xu Jinglei, et al. On the achievements and prospects for the methods of computational fluid dynamics[J]. Adv Mech, 2001, 41(5): 562-589. [3] Kuang Yuanyang, Lu Yan, Lin Zhi, et al. Coupled model analysis of the ablative Rayleigh–Taylor instability[J]. Plasma Sci Technol, 2023, 25: 055201. doi: 10.1088/2058-6272/acac64 [4] Fan Zhengfeng, Luo Jisheng, Ye Wenhua, et al. Weakly nonlinear ablative Rayleigh–Taylor instability at preheated ablation front[J]. Phys Plasmas, 2009, 16: 102104. doi: 10.1063/1.3236746 [5] Ye Wenhua, Wang Lifeng, He Xiantu. Spike deceleration and bubble acceleration in the ablative Rayleigh-Taylor instability[J]. Phys Plasmas, 2010, 17: 122704. doi: 10.1063/1.3497006 [6] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. doi: 10.1038/nature14539 [7] Zhou Feiyan, Jin Linpeng, Dong Jun. Review of convolution neural network[J]. Chin J Comput, 2017, 40(6): 1229-1251. doi: 10.11897/SP.J.1016.2017.01229 [8] Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proc IEEE, 1998, 86(11): 2278-2324. doi: 10.1109/5.726791 [9] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[J]. Commun ACM, 2017, 60(6): 84-90. doi: 10.1145/3065386 [10] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[DB/OL]. arXiv preprint arXiv: 1409.1556, 2014. [11] Szegedy C, Liu Wei, Jia Yangqing, et al. Going deeper with convolutions[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2015: 1-9. [12] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2016: 770-778. [13] Jin Xiaowei, Cheng Peng, Chen Wenli, et al. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder[J]. Phys Fluids, 2018, 30: 047105. doi: 10.1063/1.5024595 [14] Sekar V, Jiang Qinghua, Shu Chang, et al. Fast flow field prediction over airfoils using deep learning approach[J]. Phys Fluids, 2019, 31: 057103. doi: 10.1063/1.5094943 [15] Fukami K, Fukagata K, Taira K. Super-resolution reconstruction of turbulent flows with machine learning[J]. J Fluid Mech, 2019, 870: 106-120. doi: 10.1017/jfm.2019.238 [16] Deng Zhiwen, He Chuangxin, Liu Yingzheng, et al. Super-resolution reconstruction of turbulent velocity fields using a generative adversarial network-based artificial intelligence framework[J]. Phys Fluids, 2019, 31: 125111. doi: 10.1063/1.5127031 [17] Liu Bo, Tang Jiupeng, Huang Haibo, et al. Deep learning methods for super-resolution reconstruction of turbulent flows[J]. Phys Fluids, 2020, 32: 025105. doi: 10.1063/1.5140772 [18] Zhou Xuhui, McClure J E, Chen Cheng, et al. Neural network–based pore flow field prediction in porous media using super resolution[J]. Phys Rev Fluid, 2022, 7: 074302. doi: 10.1103/PhysRevFluids.7.074302 [19] Jagodinski E, Zhu Xingquan, Verma S. Inverse identification of dynamically important regions in turbulent flows using three-dimensional convolutional neural networks[J]. Phys Rev Fluids, 2023, 8: 094605. doi: 10.1103/PhysRevFluids.8.094605 [20] Gallis M A, Koehler T P, Torczynski J R, et al. Direct simulation Monte Carlo investigation of the Rayleigh-Taylor instability[J]. Phys Rev Fluids, 2016, 1: 043403. doi: 10.1103/PhysRevFluids.1.043403 [21] Fu Chengquan, Zhao Zhiye, Xu Xin, et al. Nonlinear saturation of bubble evolution in a two-dimensional single-mode stratified compressible Rayleigh-Taylor instability[J]. Phys Rev Fluids, 2022, 7: 023902. doi: 10.1103/PhysRevFluids.7.023902 [22] Piriz A R, Cortázar O D, López Cela J J, et al. The Rayleigh-Taylor instability[J]. Am J Phys, 2006, 74(12): 1095-1098. doi: 10.1119/1.2358158 [23] Zhong Baojiang, Lu Zhifang, Ji Jiahuan. Review on image interpolation techniques[J]. J Data Acquis Process, 2016, 31(6): 1083-1096. [24] Shi Wenzhe, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2016: 1874-1883. [25] Wang Mengjie, Yang Xiaomin, Anisetti M, et al. Image super-resolution via enhanced multi-scale residual network[J]. J Parallel Distrib Comput, 2021, 152: 57-66. doi: 10.1016/j.jpdc.2021.02.016 [26] Kingma D P, Ba J. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations. 2015. -





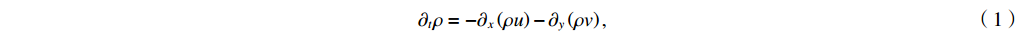
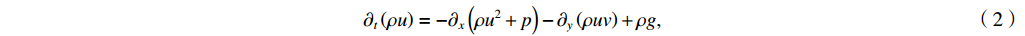
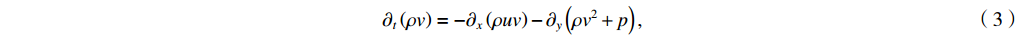
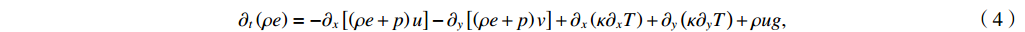
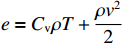
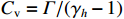
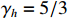
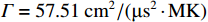
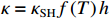
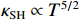
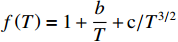
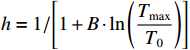
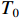
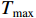
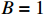

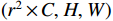
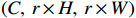

 DownLoad:
DownLoad:

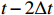
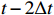
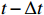
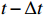
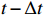

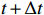
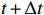
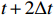
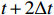
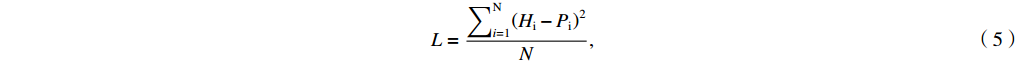
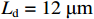



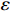





 下载:
下载: