Effect of plasma on transmission characteristics of high-frequency microwave
-
摘要: 研究高频微波在等离子体中的传输特性能有效地分析评估在微波通信和雷达技术中信息的传递过程。通过使用数值仿真的方法分析了等离子体电子密度、厚度及入射波频率对微波反射、吸收和透射的影响。结果显示,等离子体厚度和电子密度增加会导致吸收增强、透射减弱;且反射会随厚度降低和电子密度升高而微弱升高;高频微波更易于穿透等离子体,透射随频率提高而增强。此外,研究结果表明电子密度不仅能影响能量的传输,还会影响电磁波波形,使其展宽。高密度等离子体会明显导致微波波形时空上延展增宽,非弹性碰撞使得增宽现象明显。波形的改变规律能为雷达回波和微波通信所携带信息的复原工作提供一定的理论支撑。Abstract: Studying the transmission characteristics of high-frequency microwaves in plasma can effectively analyze and assess the information transfer process in microwave communication and radar technology. Numerical simulations were employed to analyze the effects of plasma electron density, thickness, and incident wave frequency on microwave reflection, absorption, and transmission. The results indicate that increased plasma thickness and electron density lead to enhanced absorption and reduced transmission; reflection increases slightly with decreased thickness and increased electron density. High-frequency microwaves are more easily transmitted through plasma, with transmission enhancing as frequency increases. Furthermore, the research shows that electron density not only affects energy transmission but also alters the electromagnetic wave shape, causing its broadening. High-density plasma significantly broadens microwave waveforms both spatially and temporally, with inelastic collisions contributing prominently to this broadening. The patterns of waveform changes can provide theoretical support for the restoration of information carried by radar echoes and microwave communications.
-
受控热核聚变是解决人类能源危机的主要途径之一。聚变能是无污染、资源丰富的理想能源,实现受控核聚变将从根本上解决人类社会的能源问题。磁约束核聚变是实现受控核聚变的重要途径之一,目前世界各国已在磁约束核聚变理论、关键技术上取得了突破性进展。在磁约束核聚变实验中,需要使用高功率毫米波源进行电子回旋共振加热(ECRH)[1]。而在毫米波频段,回旋管是唯一能产生高功率(>1 MW)连续波输出的器件,因而被广泛应用到热核聚变实验中。目前磁约束核聚变技术在国内外得到较快发展,同时也对回旋管提出了更高的要求:不仅提出了MW级功率输出、工作时间时长的要求,还提出了双频点或多频点可调谐工作的要求[2]。一般来说,MW级回旋管要求准光模式变换器衍射损耗低于5%[3-5]。目前,俄罗斯的Gycom公司设计了170 GHz和135 GHz MW级双频回旋管,其准光模式变换器效率分别为99.19%(170 GHz)和97.42%(135 GHz)[6]。国际上德国、日本、美国等国家的研究机构也完成了双频MW级回旋管内置准光模式变换器的研制工作[7-11]。国内的科研机构也开展了准光模式变换器的研究工作[12-18]。在双频(多频)准光模式变换器设计方面,北京大学进行了太赫兹多模式准光模式变换器的设计[16-17],电子科技大学也对准光模式变换器的带宽进行了研究[18],但在国内尚未见到MW级双频回旋管内置准光模式变换器的公开报道。双频回旋管研制的难点之一就是准光模式变换器的双频复用,通常针对某个频率和模式优化得到的准光系统与针对另一个频率和模式为目标优化得到的准光系统存在较大差异,会产生较大损耗和造成高斯含量的降低,无法满足MW级双频连续波回旋管的需求。如参考文献[19]中,未针对镜面系统进行多频设计,导致各个频率下的高斯含量差异较大。针对这一问题,本文开展了双频准光模式变换器的设计。通过选择圆波导内传播模型近似的传播模式,并利用数值方法在圆波导内壁引入不规则微扰,将圆波导口输入的高阶腔体模式转换为准高斯模式,本文完成了双频预聚束辐射器的设计。在后续双频镜面系统设计中,本文基于标量衍射理论,并在KS迭代算法[20]中引入权重和最小均方法等方法完成了双频相位修正镜设计,进一步将准高斯波束修正为高斯波束。仿真结果显示所设计的准光模式变换器能满足MW级双频回旋管的要求。
1. 双频准光模式变换器设计
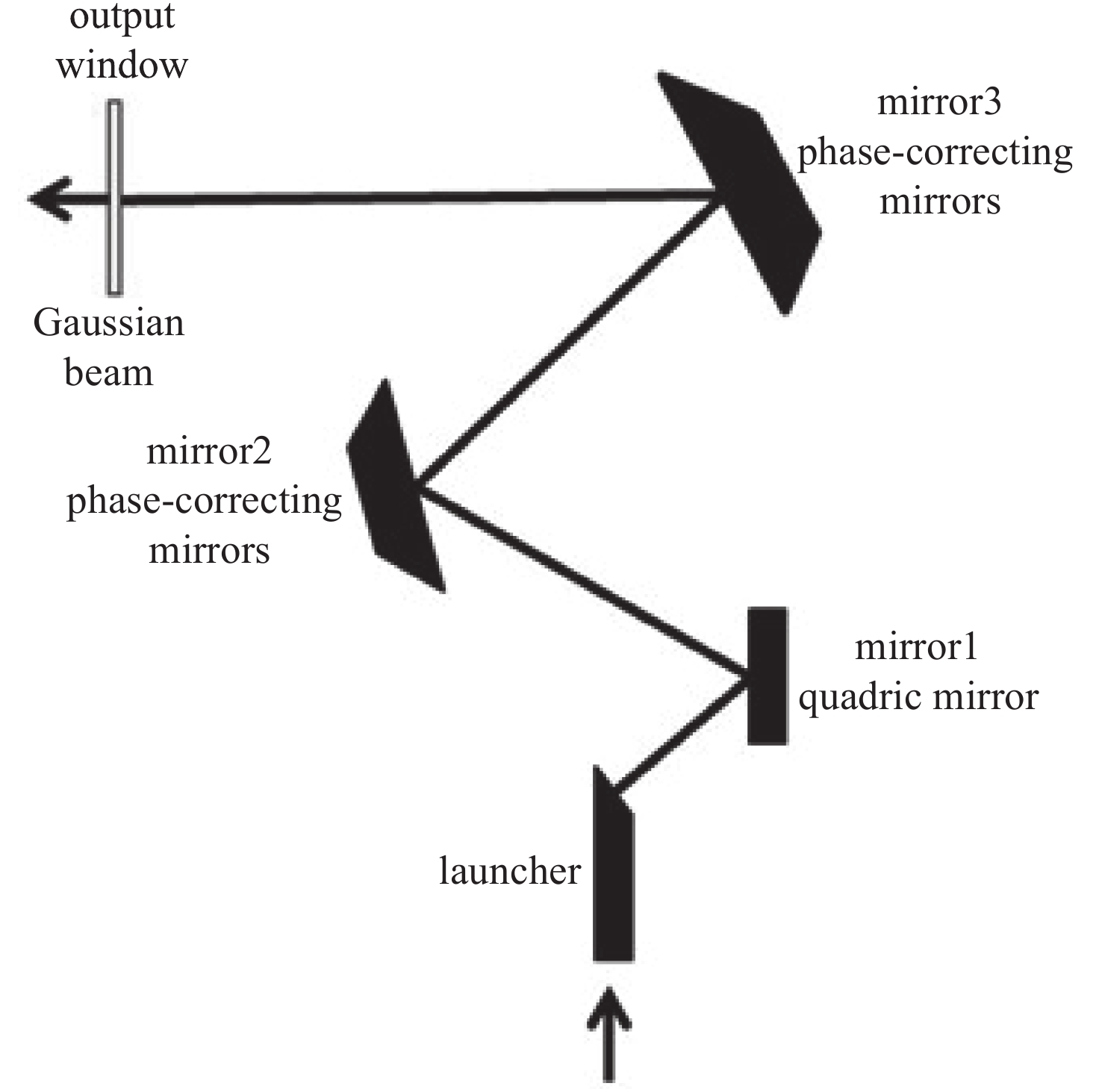
准光模式变换器包括一个预聚束辐射器和后续的反射镜面系统,如图1所示。辐射器将回旋管产生的TE0,n或TEm,n模式进行预聚束,并通过切口处辐射至后续镜面系统。后续镜面系统进一步对波束传播方向和相位进行修正,最终修正为高斯波束(TEM00)输出。针对目前以单一频率为优化目标的准光模式变换器设计方法会造成两个频率之间准光系统差异较大,本文将两个频率同时设为优化目标(既需要保持较低衍射损耗,同时获得尽可能高的高斯含量),并通过筛选圆波导内传播模型近似的模式,在迭代算法中引入权重、最小均方法分别完成了双频辐射器和双频相位修正镜的设计。
1.1 双频辐射器设计
辐射器主要包括Vlasov型辐射器[21-22]、Denisov型预聚束辐射器[23]、不规则微扰型预聚束辐射器[3]三种。Vlasov型辐射器损耗较大,聚束效果较差。Denisov型辐射器通过对两组周期微扰进行优化将高阶模式变换为该模式与8个卫星模式的混合模式,使得波导内的场呈现为准高斯分布。但Denisov型辐射器在过低阶模式和圆对称模式难以形成有效的卫星模式,过高阶的模式需要较长的微扰段。且对于一些
π/θ (θ 为波束角向传播方向与角向单位矢量的夹角)不接近于整数的高阶边廊模式,基于耦合模理论的Denisov辐射器无法获得足够的变换效率[16]。不规则微扰型预聚束辐射器通过数值方法在圆波导内壁引入不规则微扰,将圆波导口输入的高阶腔体模式转换为准高斯模式。不规则微扰型预聚束辐射器比Denisov型预聚束辐射器在模式选择上更具普适性,结构也更为紧凑,因此本文选择不规则微扰型辐射器作为双频准光模式变换器的辐射器。由于辐射器圆波导半径远大于回旋管的工作频率所对应的自由空间波长,因此电磁波在波导内的传播情况可以采用几何光学进行分析。可以考虑通过电磁波在圆波导内的传输参数逆向选择合适的传播模式。通过对105 GHz和140 GHz的多个模式在圆波导中的传播情况进行分析,我们最后选择了105 GHz(TE18,7)和140 GHz(TE24,9),两者在圆波导中的传播参数如表1所示,105 GHz(TE18,7)和140 GHz(TE24,9)在圆波导内传播的布里渊区参数、焦散圆半径等参数非常接近,两者在圆波导内的几何光学传播模型近似,有利于高效率双频辐射器的设计。
表 1 两种模式在圆波导中的传播参数Table 1. Propagation parameters of the circular waveguide for considered modesmode frequency/GHz waveguide radius/mm caustic radius/mm pitch distance/mm axial bounce angle/(°) TE18,7 105 21.5 8.76 41.1 73.1 TE24,9 140 21.5 8.80 42.6 72.4 利用标量衍射理论,结合KS迭代算法,可快速求解波导内壁电流分布和逆向求解辐射器内壁微扰分布。
u(r)=−∬[u(r0)∇G(r,r0)−G(r,r0)∇u(r0)]n0⋅ds0 (1) G(r,r0)=exp(±jk|r−r0|)4π|r−r0| (2) 式中:
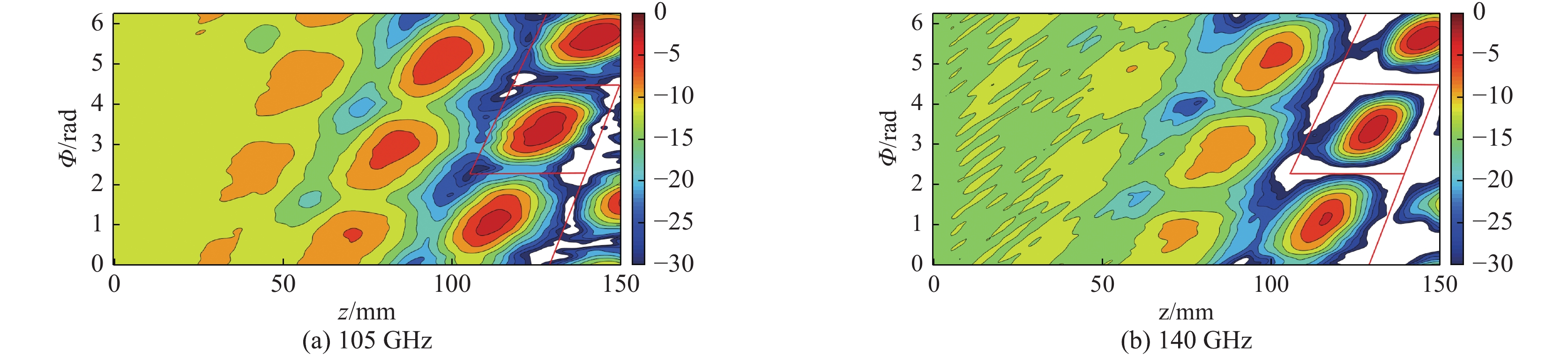
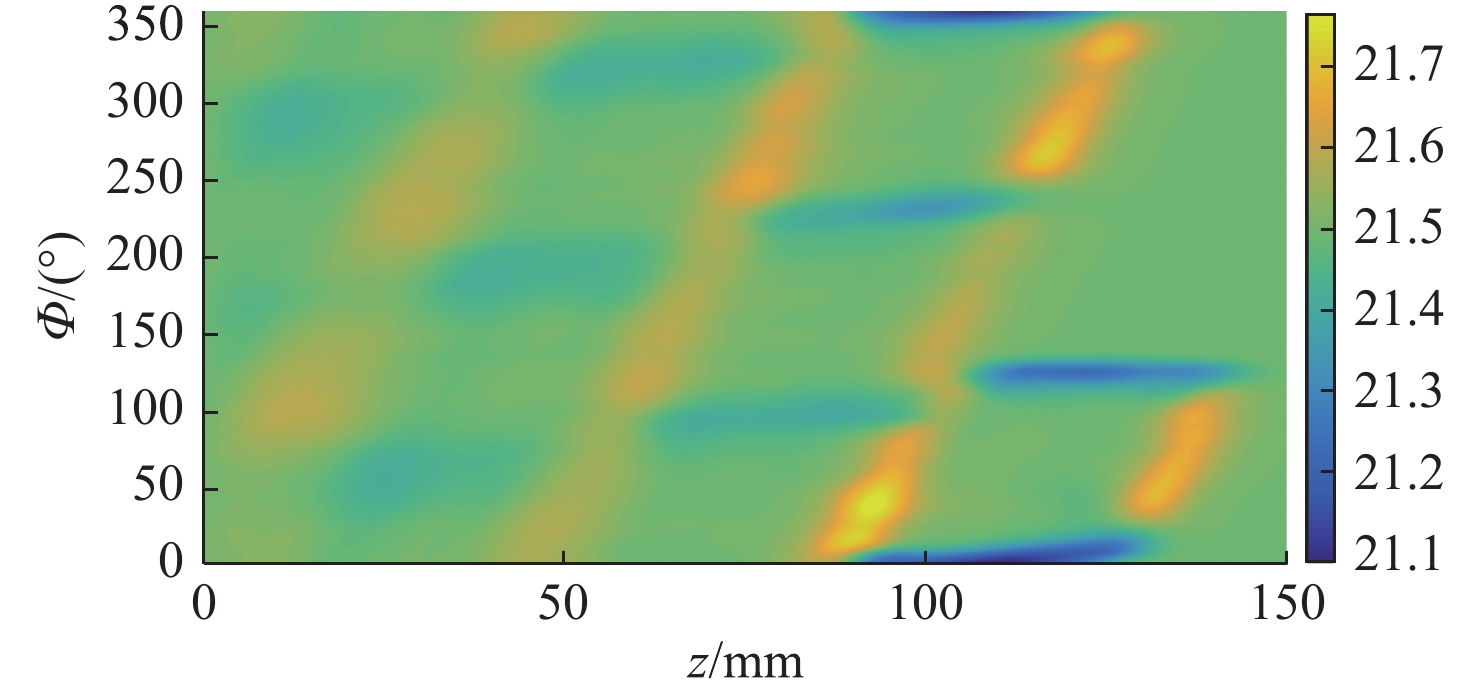
n0 是波导壁的法向矢量;k 是波数;G(r,r0) 表示自由空间格林函数如式(2)中所示;u(r) 表示波导壁上的场分布[18]。两个工作频率的圆波导沿径向展开的壁电流分布如图2(图中红色线表示螺旋切口的位置和辐射场),辐射器内壁微扰分布如图3所示。辐射器长度140 mm,螺旋切口长度35 mm。经螺旋切口辐射,入射在与辐射器同圆心、半径为5 cm的圆柱面上的场分布如图4所示。由图2和图4可见从波导端口馈入的高阶腔体模式经过辐射器微扰修正,逐渐转换为准高斯波束,且辐射波束旁瓣较低,实现了预聚束。
1.2 双频相位修正镜设计
经过辐射器螺旋切口辐射出的电磁波经过第一个镜面的反射,还需利用相位修正镜将入射的准高斯波束精确修正为所需束腰大小的高斯波束。相位修正镜的原理类似于相控阵天线,镜面上每一点类似于相位控制元件,相控阵天线理论表明足够数量的相位控制元件可以控制波束的方向和方向图,同样通过对反射镜面进行赋形也可以改变镜面上的电流相位和分布以得到期望的波束[8]。
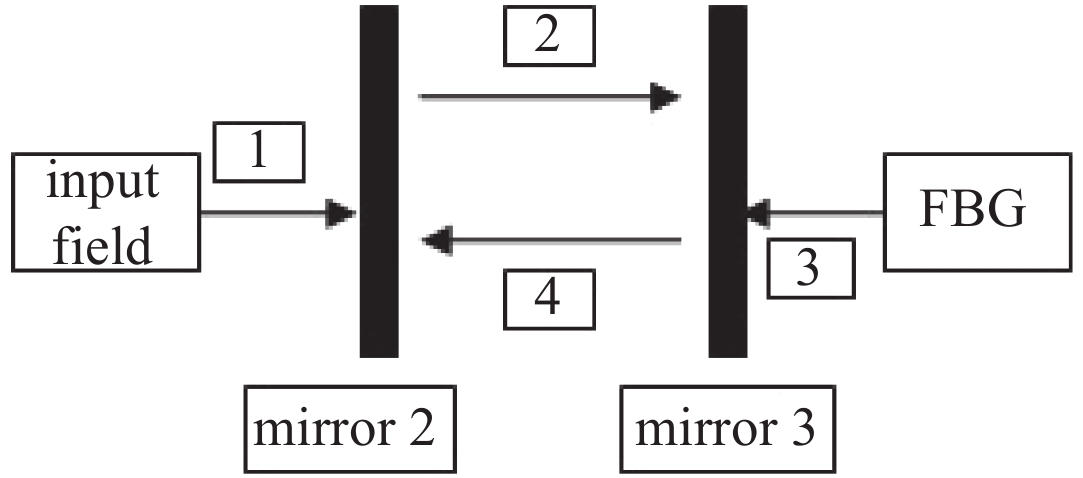
相位修正镜的设计采用标量衍射理论、KS迭代算法、几何光学等方法。相位修正镜面采用的设计流程如图5所示。首先利用衍射理论将入射波传播至镜面(如图中序号1,2所示),然后将理想高斯波束反向传播至镜面(如图中序号3,4所示),此时通过比较正向传播至镜面和反向传播至镜面上的场可以得到相位差。利用相位差可得到镜面的相位修正尺寸,再结合KS迭代算法就可以逆向得到相位修正镜镜面。
由图2可以看出,经由辐射器出射的场存在差异,仅针对某个单一频率进行优化的相位修正镜并不能同时适用于另一个频率。为了避免造成较大损耗和高斯含量的下降,减小两个工作频率之间准光模式变换器性能的差异,我们考虑将两个目标频率同时设为优化目标进行优化,同时在KS迭代算法中引入了权重和最小均方法优化以加快寻优。定义成本函数如下
P=∬∑m[wm|vmδy−δθm|2]dxdz (3) ∂P∂δy=0 (4) 给两个频率分别赋予权重
wm=|Em|2∑m|Em|2 (5) 式中:
δy 是镜面表面的相位修正的尺寸;wm 是第m 个频率的权重;θm 是第m 个频率的相位差;vm 是与频率有关的值,Em 是第m 个频率对应的电场。我们通过式(3)~(5)得出了双频镜面的修正尺寸δy 再结合前文提到的方法完成了双频相位修正镜的设计。2. 仿真分析
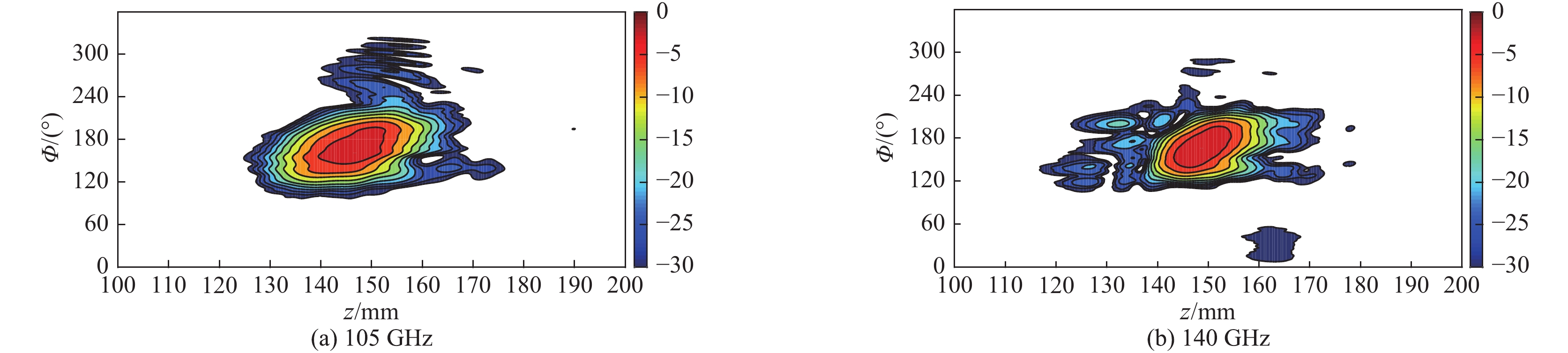
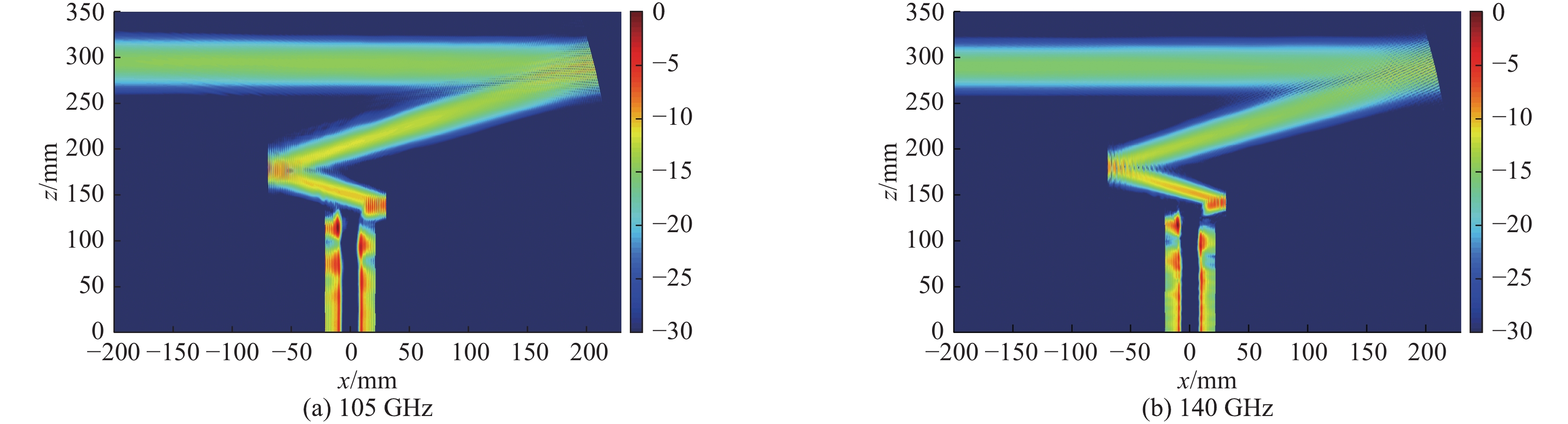
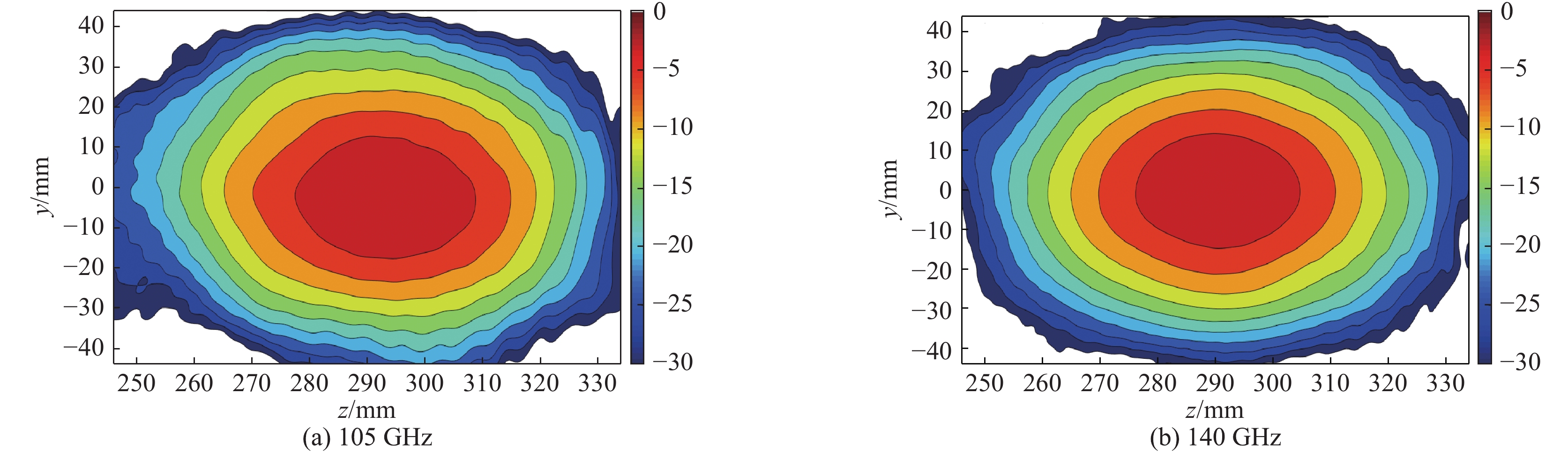
经过仿真软件(算法为MLFMM)计算105 GHz和140 GHz双频准光模式变换器的xz平面电场传播情况和回旋管窗片上的场分布如图6、图7所示。图6(a)为105 GHz时准光模式变换器截面的电场传播图,图6(b)为140 GHz时截面上的电场传播图。从图6中可以看出波导端输入的高阶腔体模式经过波导内壁微扰逐渐被转换为准高斯模式,从辐射器出射时电场幅值达到了最大值且实现了聚束,随后经后续镜面系统调整传播方向以及相位修正,将入射波束的束腰修正为期望的束腰大小,最终从回旋管窗片输出,电磁波在整个双频准光模式变换器中的传播过程中衍射损耗低于−30 dB,回旋管窗片(直径88 mm)边缘的电场幅度低于−27 dB,电场幅值也呈现高斯分布,如图7所示。图7(a)为105 GHz窗片上的电场分布图,图7(b)为140 GHz窗片上的电场分布情况。
经过分析计算得到结果如表2所示,本文设计的双频准光模式变换器在工作频率140 GHz(TE24,9)时能量传输效率为99.0%、高斯含量大于99.0%,场强最大值点偏移z向0.50 mm,y向0.50 mm;工作频率为105 GHz(TE18,7)时能量传输效率大于97.0%、高斯含量为98.0%,场强最大值点偏移z向2.00 mm,y向2.25 mm。较好地实现了模式转换和能量传输。其中能量传输效率的定义为
表 2 仿真结果Table 2. Results of simulationmode frequency/GHz Gaussian content/% conversion efficiency/% z-offset/mm y-offset/mm TE18,7 105 98.0 97.3 2.00 2.25 TE24,9 140 99.7 99.0 0.50 0.50 η=P1P2 (6) 高斯含量定义为
c=∬s|Ax||Bx|ds√∬s|Ax|2ds∬s|Bx|2ds (7) 式中:
P1 表示回旋管窗片位置处的功率;P2 表示辐射器入口处的输入功率。Ax 表示回旋管窗片位置处的电场分布,Bx 表示理想高斯分布。3. 结 论
本文通过对毫米波在圆波导内的传输参数进行分析,选择圆波导内传播模型近似的传播模式,并利用数值方法在圆波导内壁引入不规则微扰,将圆波导口输入的高阶腔体模式转换为准高斯模式,完成了双频预聚束辐射器的设计;考虑到两个工作频率下经双频辐射器出射的场分布有差异,在迭代算法中引入权重并结合最小均方法等方法完成了双频相位修正镜面的设计,最终实现将输入的波束修正为期望束腰的高斯波束,准光模式变换器中衍射损耗较低,能满足MW级双频回旋管的要求。今后将考虑引入新的优化方法对双频辐射器的设计进一步优化,同时探索多频准光模式变换器的设计方法。
-
表 1 不同等离子体厚度时反射、吸收、透射
Table 1. Reflection, absorption and transmission in different plasma thickness
plasma thickness/mm reflectivity/% absorptivity/% transmissivity/% 20 1.2 74.8 24.0 26 0.9 91.1 8.10 -
[1] Poorreza E, Gargari N D. Modeling and simulation of a microwave-assisted plasma with different input power for plasma-based applications[J]. Russian Journal of Physical Chemistry B, 2023, 17(3): 719-724. doi: 10.1134/S1990793123030235 [2] Ikeda Y, Soriano J K, Kawahara N, et al. Spatially and temporally resolved plasma formation on alumina target in microwave-enhanced laser-induced breakdown spectroscopy[J]. Spectrochimica Acta Part B: Atomic Spectroscopy, 2022, 197: 106533. doi: 10.1016/j.sab.2022.106533 [3] Zhang Chaoyang, Fu Wenjie, Hu Shijie, et al. Investigation on continuous and modulated microwave plasma filaments at atmospheric pressure[J]. IEEE Access, 2021, 9: 154318-154323. doi: 10.1109/ACCESS.2021.3128610 [4] Barnes B K, Ouro-Koura H, Derickson J, et al. Plasma generation by household microwave oven for surface modification and other emerging applications[J]. American Journal of Physics, 2021, 89(4): 372-282. doi: 10.1119/10.0002706 [5] Zhao Chengwei, Li Xiaoping, Liu Yanming, et al. Research on plasma electron density distribution based on microwave diffraction[J]. Plasma Sources Science and Technology, 2022, 31: 015007. doi: 10.1088/1361-6595/ac39ad [6] Ye Xin, Wang Yongge, Yao Jingfeng, et al. Plasma-enabled microwave modulation for continuous beam scanning[J]. Journal of Physics D: Applied Physics, 2022, 55: 435202. doi: 10.1088/1361-6463/ac8da1 [7] Zhang Jianwei, Luo Wei, Jiang Ming, et al. Plasma propagation in the microwave window breakdown at the air/dielectric interface[J]. Plasma Sources Science and Technology, 2020, 29: 025013. doi: 10.1088/1361-6595/ab6e59 [8] Mu Xiangchao, Dong Guoxiang, Li Xiaoping, et al. Analysis of the electromagnetic wave transmission characteristics in inhomogeneous plasma based on an equivalent circuit model[J]. IEEE Transactions on Plasma Science, 2024, 52(3): 698-706. doi: 10.1109/TPS.2024.3371100 [9] Noori E. Investigation of near cut-off properties of electromagnetic wave propagation in homogeneous, collisional plasma slab[J]. Contributions to Plasma Physics, 2022, 62: e202200016. doi: 10.1002/ctpp.202200016 [10] Zhang Chaoyang, Chen Chi, Fu Wenjie, et al. Investigation on the microwave excited plasma filament at atmospheric pressure[J]. IEEE Transactions on Plasma Science, 2021, 49(6): 1877-1881. doi: 10.1109/TPS.2021.3075574 [11] Zhao Yuexing, Su Ruiming, Ma Jinping, et al. SO-FDTD simulation on the transmission characteristics of terahertz waves in inhomogeneous magnetized dusty plasma[J]. The European Physical Journal D, 2024, 78: 32. doi: 10.1140/epjd/s10053-024-00824-8 [12] Wan Xiaohuan, Zhou Zhikun, Zhang Juan, et al. Propagation characteristics of obliquely incident terahertz waves in high-temperature magnetized plasma[J]. IEEE Transactions on Plasma Science, 2022, 50(2): 241-249. doi: 10.1109/TPS.2021.3139373 [13] Zhou Zhikun, Wan Xiaohuan, Zhang Juan, et al. Influence of temperature on terahertz waves propagating in magnetized plasma[J]. Physica Scripta, 2021, 96: 075607. doi: 10.1088/1402-4896/abfcf1 [14] Shen Fangfang, Zhang Zhongdao, Bai Bowen, et al. Research on the reflection characteristics of the broadband electromagnetic wave in nonuniform plasma[J]. IEEE Transactions on Plasma Science, 2024, 52(3): 657-665. doi: 10.1109/TPS.2024.3373645 [15] Zhang Jie, Li Miao, Han Bing. Analysis of electromagnetic waves reflected by re-entry plasma sheath based on CSO-FDTD[J]. Physica Scripta, 2023, 98: 095610. doi: 10.1088/1402-4896/acf0f9 [16] Zhang Youyi, Xu Guanjun, Zheng Zhengqi. Terahertz waves propagation in an inhomogeneous plasma layer using the improved scattering-matrix method[J]. Waves in Random and Complex Media, 2021, 31(6): 2466-2480. doi: 10.1080/17455030.2020.1757177 [17] Lyu Xingbao, Yuan Chengxun, Avtaeva S, et al. Attenuation of microwave radiation by post-anode plasma in a composite grid electrode structure[J]. IEEE Access, 2022, 10: 7675-7683. doi: 10.1109/ACCESS.2022.3143582 [18] Vhanmore B D, Rajmane S P, Sadale S B, et al. Dominance of polarization modes and absorption on self-focusing of laser beams in collisionless magnetized plasma[J]. Journal of Nonlinear Optical Physics & Materials, 2024. [19] Chen Peiqi, Nie Qiuyue, Zhang Zhonglin, et al. Integrative implementation of scattering reduction and radiation enhancement for an electrically small antenna by subwavelength plasmas[J]. Physics of Plasmas, 2024, 31: 073503. doi: 10.1063/5.0211317 [20] Metelskii I I, Kovalev V F, Bychenkov V Y. Nonlinear laser radiation absorption due to relativistic plasma resonance in an inhomogeneous plasma[J]. Journal of Experimental and Theoretical Physics, 2021, 133(2): 236-252. doi: 10.1134/S1063776121080069 [21] Sun Jinhai, Zhao Yarui, Yin Hongcheng, et al. An open simulation model for terahertz wave transmission in plasma[J]. Journal of Applied Physics, 2024, 135: 153104. doi: 10.1063/5.0199442 [22] Desai M, Ghosh P, Kumar A, et al. Deep-learning architecture-based approach for 2-D-simulation of microwave plasma interaction[J]. IEEE Transactions on Microwave Theory and Techniques, 2022, 70(12): 5359-5368. doi: 10.1109/TMTT.2022.3217138 [23] Janicek A, Thornton E, Garrett T, et al. Length dependence on broadband microwave emission from laser-generated plasmas[J]. IEEE Transactions on Plasma Science, 2020, 48(6): 1979-1983. doi: 10.1109/TPS.2020.2988762 [24] Chang Qi, Ma Yunpeng, Liu Ji, et al. Simulation of electromagnetic waves in plasma by subdomain-level nonconformal DGTD method[J]. IEEE Transactions on Plasma Science, 2022, 50(11): 4775-4781. doi: 10.1109/TPS.2022.3214215 [25] Zhou Zhikun, Wan Xiaohuan, Li Xiaolin, et al. SO-FDTD analysis on transmission characteristics of terahertz wave in plasma[J]. Physics of Plasmas, 2021, 28: 072105. doi: 10.1063/5.0053611 [26] Wang Ge, Pan Hui, Lai Shimiao, et al. Dynamic measurement of relative complex permittivity of microwave plasma at atmospheric pressure[J]. Processes, 2021, 9: 1812. doi: 10.3390/pr9101812 [27] Yao Jingfeng, Yu Zhi, Yuan Chengxun, et al. The influence of plasma distribution on microwave reflection in a plasma-metal model[J]. IEEE Transactions on Plasma Science, 2020, 48(2): 359-363. doi: 10.1109/TPS.2019.2943519 [28] Liu Yanming, Zhang Xi, Bai Bowen, et al. A calculation method of electromagnetic wave reflection in plasma sheath environment[J]. IEEE Transactions on Plasma Science, 2022, 50(7): 2030-2038. doi: 10.1109/TPS.2022.3181220 [29] Zhang Chaoyang, Lu Dun, Hu Shijie, et al. An economic real-time microwave plasma impedance measurement method[J]. IEEE Transactions on Plasma Science, 2021, 49(11): 3503-3508. doi: 10.1109/TPS.2021.3115846 [30] Pak I H, Kim Y H, Oh C H, et al. Transmission characteristics of electromagnetic waves in a semicircular plasma filament layer generated by a femtosecond laser[J]. Contributions to Plasma Physics, 2021, 61: e202100032. doi: 10.1002/ctpp.202100032 [31] 王彦同, 帕提曼·阿不都玛洪, 石雁祥, 等. 弱电离尘埃等离子体微波衰减理论的实验研究[J]. 电波科学学报, 2020, 35(6):967-973Wang Yantong, Abudoumahong P, Shi Yanxiang, et al. Experimental study on microwave attenuation theory of weakly ionized dusty plasma[J]. Chinese Journal of Radio Science, 2020, 35(6): 967-973 [32] Moshkov A V, Pozhidaev V N. Numerical simulation of very-low-frequency waves passing through the magnetoactive plane-layered plasma of Earth's lower ionosphere[J]. Journal of Communications Technology and Electronics, 2020, 65(5): 472-479. doi: 10.1134/S1064226920050101 [33] Ma Zhu, Wei Min, Li Meng, et al. Study on electromagnetic characteristics of plasma model-based on the symplectic multiresolution time-domain scheme[J]. Modern Physics Letters B, 2020, 34: 2050046. [34] Bao Yu, He Xiang, Su Wei, et al. Study on the generation of terahertz waves in collision plasma[J]. Physics of Plasmas, 2024, 31: 093302. doi: 10.1063/5.0219947 [35] 潘惠, 王舸, 杨阳. 大气压微波等离子体射流装置放电特性研究[J]. 强激光与粒子束, 2022, 34:049001 doi: 10.11884/HPLPB202234.210277Pan Hui, Wang Ge, Yang Yang. Design and study of atmospheric pressure microwave plasma jet[J]. High Power Laser and Particle Beams, 2022, 34: 049001 doi: 10.11884/HPLPB202234.210277 [36] 陈煜青, 王蕾, 赵立山, 等. 等离子体鞘套低频通信电磁波透射率与辐照微波场强关系仿真研究[J]. 强激光与粒子束, 2023, 35:089001 doi: 10.11884/HPLPB202335.220361Chen Yuqing, Wang Lei, Zhao Lishan, et al. Simulation study of the relationship between low-frequency communication EM wave transmissivity of plasma sheaths and irradiation microwave E-field strength[J]. High Power Laser and Particle Beams, 2023, 35: 089001 doi: 10.11884/HPLPB202335.220361 -






 下载:
下载:
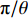
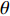
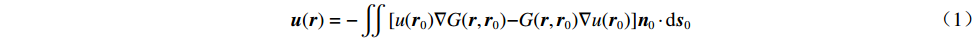
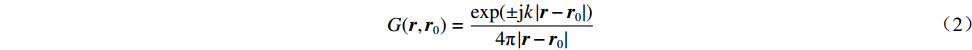
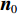
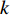
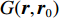
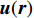




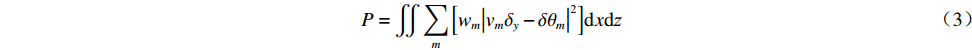
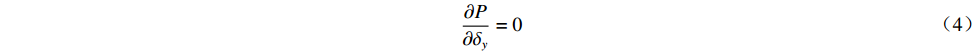
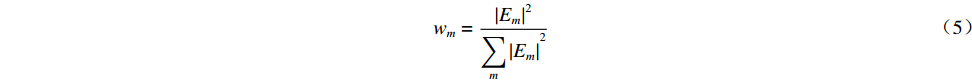
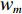
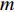
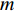
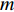
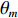
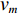
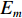


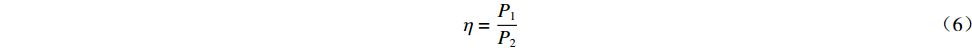
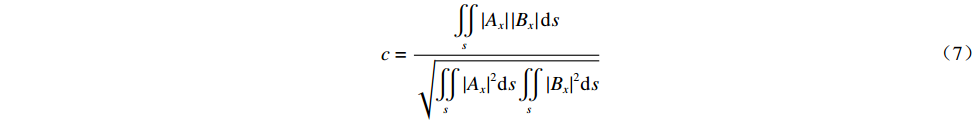
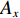
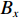

 下载:
下载: