Cascadable synchronous drive circuit for voltage controlled thyristor
-
摘要: 针对压控晶闸管脉冲工作特性和串联使用需求,设计了一种可级联的驱动电路,实现了多级串联压控晶闸管的同步开通。首先,介绍了电路拓扑及工作原理,利用推挽结构的平面耦合电感器隔离初、次级信号并传递驱动能量,解决了串联驱动小型化和低压供电条件下快前沿输出的问题;其次,通过计算和仿真确定了电路参数和主要器件选型;最后,使用6级串联的MCT作为放电开关搭建了测试电路,在充电电压8.4 kV、工作重复频率20 Hz条件下,4 Ω电阻负载上获得了幅值为1.958 kA的准方波脉冲电流。Abstract: Aiming at the pulse operating characteristics of voltage-controlled thyristors, a cascadable driving circuit is designed to realize the synchronous opening of multi-stage series-connected voltage-controlled thyristors. Firstly, the circuit topology and working principle is analysed. in which the coupled inductor is used to isolate the driver signal and transfer power to open the switch. Based on Blumlein PFN, an experimental test circuit is built, in which a 6-stage MOS-controlled thyristor is series connected to be the discharge switch. A quasi-square-wave pulse current with an amplitude of 1.958 kA is obtained on a 4 Ω resistor.
-
Key words:
- driver circuit /
- MOS-controlled thyristor /
- series connection /
- synchronization /
- quasi-square pulse
-
高增益[1-3]是速调管放大器一个重要的发展方向,增大输出腔的输出功率是提高增益的一种有效方式。如果反射功率为零,输出波导与输出腔的耦合就达到了匹配状态,输出腔的输出功率就达到了最大值。文献[4]给出了输出腔等效电路和输出功率计算公式。这里的输出腔等效电路采用变压器模型来研究输出腔与输出波导之间的耦合。输出功率计算公式是一种典型的传统算法。这种输出功率的算法得到了广泛的应用,基于圆盘模型的一维粒子模拟软件的输出功率的计算就是采用这种算法。按照传统算法,输出功率与工作频率无关,只与输出腔的间隙电压、特性阻抗和外观品质因数有关。本文提出了新的等效电路和输出功率计算公式[5-6]。输出腔等效电路以感应电流作为激励源,输出腔采用电阻、电容和电感组成并联电路,采用互感模型来研究输出腔与输出波导之间的耦合,采用传输线理论研究输出波导中的入射波和反射波。因为该模型为自洽模型,腔体通过电子束反馈回自身的效应通过感应电流来考虑,所以电子束阻抗在模型中不是必须的。当输出波导中的反射波为零时,带有调制电子束的输出腔与输出波导达到匹配状态。按照匹配理论,在匹配状态时,输出腔的工作频率与输出腔的谐振频率之间存在频率差。频率差是由输出腔的特性阻抗,感应电流和间隙电压决定的,同时还推出了匹配状态下输出腔有载品质因数的计算公式。从传统的输出腔的等效电路模型出发,无法推出完全匹配时输出腔谐振频率与有载品质因数的表达式。本文建立了较完整的带有电子束和输出波导的输出腔匹配理论即最大输出功率理论,推导了输出波导与带有电子束的输出腔之间任意的耦合和完全匹配这两种情形时输出微波功率和间隙电压关系的公式。将匹配情形时从含有互感的等效电路模型推出的输出功率的公式与传统的经典理论的公式进行比较,发现两者近似相等。
这套理论不仅得出了一般情形时输出功率与间隙电压等参量的关系式,而且可以得出匹配情形时(输出波导内反射波为零)的输出功率与间隙电压等参量的关系式,以及匹配情形时的工作频率和输出腔的谐振频率两者之间关系式和有载品质因数的表达式。根据这两个表达式就可以计算出输出腔的谐振频率和外观品质因数,这两个参数可以作为输出腔的设计依据。
1. 腔体模型
图1给出了输出腔的等效电路模型[4-9]。图1中
ig 是在与腔体耦合的输出波导中产生的出射电流,ir 是波导中的反向电流,Z0 是波导特性阻抗,R是腔体并联电阻,L是腔体电感,C是腔体电容,i是腔体电路中流过互感M的电流,id=M′i1 是腔体电路中由于调制电子束而引起的电流,通常被称为感应电流,M′ 是电子束和输出腔之间的耦合系数,i1 是束流的一次谐波。腔体和波导通过互感M互相耦合。输出腔阻抗Zcav 由腔体并联阻抗R,腔体电容C,腔体电感L或者由R、腔体谐振频率f0 、工作频率f和腔体特性阻抗R/RQQ 给出1Zcav=1R+jωC+1jωL=1R+j(ff0−f0f)1R/RQQ (1) 这两种定义通过
R/RQQ=1/12π f02π f0C 和(2π f0)2CL=1 相联系。腔体间隙电压定义为在位置矢量r=(x,y,z) 处腔体射频电场沿着某个感兴趣的路径S瞬时线积分Vgap(t)=∫SE(r,t)⋅dl (2) 腔体间隙电压是图1中腔体阻抗两端的电压,由下式给出
Vgap=−Zcav(id−i) (3) 2. 外耦合模型
这里我们将定义输出腔与外部波导耦合的模型。外部波导中同时存在带有电流ig和电压igZ0的出射波以及电流
−ir 和电压irZ0的反射波。利用图1和互感的定义,我们可以得出腔体-波导电路中电流的表达式ig+ir=jωMZ0i (4) ir−ig=(id−i)ZcavjωM (5) 式中:
ω=2πf 是工作角频率。2.1 有载品质因数Q
首先我们将给出没有电子束和外部微波源关闭时的有载品质因数Q。冷腔有载品质因数定义为
Ql=ωEstoredPloss (6) 式中:
Estored 是腔体中平均储能,表示为Estored=141ω2C|iC|2+14L|iL|2 (7) 式中:
iC 是流过电容器的电流,iL 是流过电感的电流,平均功率损耗为Ploss=PG+Pe=12R|iR|2+12Z0|ig|2 (8) 式中:
iR 是流过腔体电阻的电流,PG 为腔体电阻损耗功率,Pe 为从腔体泄漏到波导中的功率。在无反射波的情形下(ir=0) 有ig=−(id−i)ZcavjωM (9) iR=−Zcav(id−i)1R (10) iL=−Zcav(id−i)1jωL (11) iC=−Zcav(id−i)jωC (12) 我们定义复耦合系数
β 为β=Z0Zcavω2M2 (13) 根据腔体与波导耦合系数
β′ 的定义β′=PePG=Z0Rω2M2=βRZcav (14) 没有电子束的有载品质因数为
QL=Q011+β′=Q011+βR/βRZcavZcav (15) 其中固有品质因数
Q0=ωCR2(1+1ω2CL) (16) 2.2 反射微波功率
反射微波功率为
Pr=12Z0|ir|2 (17) 从式(4)和式(5)中消去出射波,我们可以得到腔内驱动电流为
i=2ir−idZcavjωMjωMZ0(1+β) (18) 这个表达式可以用来推出间隙电压
Vgap=−Zcav(id−i)=−idZcav1+β−j2irωM1+ββ (19) 或者反过来,波导中的反射波为
ir=−1+βj2ωMβ(Vgap+idZcav1+β) (20) 从这个表达式可以导出一般情形时反射微波功率为
Pr=18|1+β|2|Vgap+idZcav1+β|2|Zcav||β| (21) 2.3 输出微波功率
输出微波功率为
Pg=12Z0|ig|2 (22) 下面分两种情形讨论。
1)当复耦合系数
β 不等于1时:从式(4)和式(5)中消去反射波,我们可以得到腔内驱动电流为i=2ig+idZcavjωMjωMZ0(1−β) (23) 这个表达式可以用来推出间隙电压
Vgap=−Zcav(id−i)=−idZcav1−β−j2igωM1−ββ (24) 或者反过来,波导中的出射波为
ig=−1−βj2ωMβ(Vgap+idZcav1−β) (25) 从这个表达式可以导出输出波导中的输出微波功率为
Pg1=18|1−β|2|Vgap+idZcav1−β|2|Zcav||β| (26) 2)当复耦合系数
β 等于1时:从式(4)和式(5)中消去反射波,我们可以得到出射电流为ig=−idZcav2jωM (27) 将式(27)代入式(22)可以导出输出微波功率为
Pg2=18|id|2|Zcav| (28) 3. 匹配耦合的特殊情形
如果输出波导中没有反射波,波导与腔体的耦合就达到了匹配。因为匹配将导致输出微波功率达到最大值,所以波导与腔体的匹配是波导和腔体的设计目标。
3.1 输出微波功率
从式(4)和式(5)得到
2ir=ijωMZ0+(id−i)ZcavjωM (29) 令
ir 为零可以导出i(1+β)=idβ (30) 式(30)为匹配条件。在这种情形下,间隙电压为
Vgap=−Zcavid1+β (31) 或者
Vgap+idZcav1−β=2Vgapββ−1 (32) 与这个条件相对应,匹配时输出微波功率为
Pg1=12|β||Vgap|2|Zcav| (33) 对于匹配条件式(30)必须满足,或者
β=iid−i (34) 匹配时输出微波功率又可以写为
Pg1=12Z0|ig|2=12ω2M2Z0|β|2|1+β|2|id|2 (35) 由
β 的定义式(13)和式(33)与式(15)可得Pg1=12|β||Zcav||Vgap|2=12|Vgap|2Q0−QLQLR (36) 3.2 匹配时的微波频率与有载品质因数
通过比较复耦合系数
β 的定义式(13)和式(31),可以得出ω2M2=Z0−id/−idVgapVgap−1/1ZcavZcav (37) 这个方程等式左边为实数,右边通过工作频率的合适的选择也可以成为实数。定义
(δ+1)f=f0 ,如果δ 满足δ=R/RQQ2Im(id/idVgapVgap) (38) 则式(37)右边成为实数。匹配时有载品质因数为
QLt=Q011+Re(−id/−idVgapVgap−1/1ZcavZcav)R (39) 4. 从含有互感的等效电路模型推出的理论与经典理论的比较
从谐振腔的一般理论[4]可以得出
Pg=12Re(idV∗gap)=12|Vgap|21(R/RQQ)Qext (40) 这里我们把它称为经典理论。对于输出腔来说,
Qext 远小于Q0 ,QL≈Qext ,R/RQQ≈R/R(Q0−QL)(Q0−QL) ,匹配情形时的式(36)与式(40)近似相等。一般情形时的式(26)与式(40)只有通过数值计算进行比较。5. 输出腔的理论计算与粒子模拟的比较
单重入输出腔的2维粒子模拟结构图如图2所示。图2中输出腔外径为5.6 cm,输出同轴线的内外径分别为5.2 cm和5.5 cm,特性阻抗
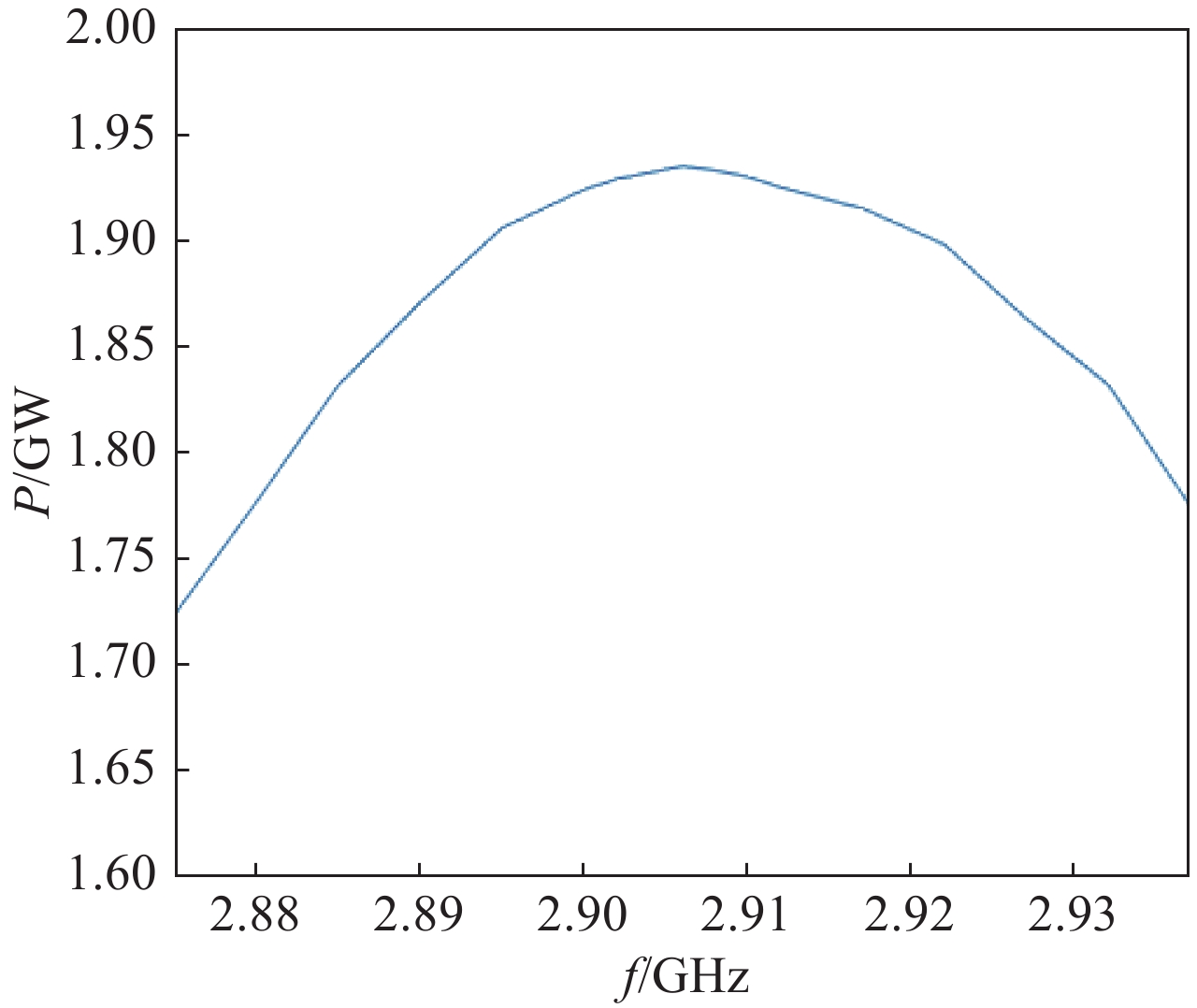
Z0 为3.365 Ω,间隙距离为1.4 cm,ra 和rb 分别等于2.4 cm和2.8 cm,为环形电子束的内半径和外半径,Rc 等于3.0 cm为漂移管半径,鼻锥厚度为6 mm。在粒子模拟中束压为724.4 kV,束流为8[1+1.2sin(2πft)] kA,外加均匀磁场为1.2 T。输入腔谐振频率f0 为2.933 GHz,特性阻抗R/RQQ 为6.727 Ω,固有品质因数Q0 为4 406.7,外观品质因数Qext 为18.8,图1中R为29 643.871 Ω,L为0.365×10−9 H,C为8.07 pF。当基波电流调制系数为1.2时,采用2维粒子模拟计算了输出微波功率与工作频率关系,计算结果如图3所示。从图3可知,当工作频率为2.906 GHz时,输出微波功率达到最大值;输出腔间隙耦合系数为0.635 9,基波电流为−9.6 kA,间隙电压为(6.767×105+2.742×105i) kV,复耦合系数为
3.5276 ×10−2+2.875 3 i,互感为1.1299 ×10−9 H,腔体阻抗为(4.461+3.636×10−2 i)Ω。根据式(38)可以得出δ 为0.010 6,所以匹配时工作频率为2.902 3 GHz,工作频率的理论值与粒子模拟的工作频率相差3.7 MHz。根据式(39)可以得出匹配时有载品质因数理论值为19.18,而粒子模拟的有载品质因数为18.72,两者相差0.46。按照式(21)计算的反射功率为1.5962 MW。按照式(26)计算的输出微波功率为2.058 GW,粒子模拟为1.935 GW,两者相差0.123 GW。按照式(36)计算的输出微波功率为2.107 6 GW。6. 结 论
匹配理论不仅得出了一般情形时输出功率与间隙电压等参量的关系式,而且可以得出匹配情形时(输出波导内反射波为零)的输出功率与间隙电压等参量的关系式,以及匹配情形时的工作频率和输出腔的谐振频率两者之间关系式和有载品质因数的表达式。根据这两个表达式就可以计算出输出腔的谐振频率和外观品质因数,这两个参数可以作为输出腔的设计依据。匹配情形时从含有互感的等效电路模型推出的输出功率的计算结果与经典理论的计算结果近似相等。
-
表 1 耦合电感器参数
Table 1. Parameters of coupling inductor
L(P1)/nH L(P2)/nH L(S1, S2)/nH Lm(P1-S1, S2)/nH Lm(P2-S1, S2)/nH 173 139 639 233 203 -
[1] 饶俊峰, 宋子鸣, 王永刚, 等. 基于磁隔离驱动的亚微秒高压脉冲电源[J]. 强激光与粒子束, 2021, 33:115002 doi: 10.11884/HPLPB202133.210332Rao Junfeng, Song Ziming, Wang Yonggang, et al. Sub-microsecond high voltage pulse power supply based on magnetic isolated driving[J]. High Power Laser and Particle Beams, 2021, 33: 115002 doi: 10.11884/HPLPB202133.210332 [2] He Dazhao, Sun Wenjie, Liao Yixin, et al. A novel high-voltage solid-state switch based on the SiC MOSFET series and its overcurrent protection[J]. High Voltage, 2023, 8(4): 698-706. doi: 10.1049/hve2.12285 [3] Jiang W, Oshima N, Yokoo T, et al. Repetitive pulsed power based on semiconductor switching devices[C]//Proceedings of 2007 16th IEEE International Pulsed Power Conference. 2007: 550-552. [4] 李玺钦, 吴红光, 栾崇彪, 等. 基于MOSFET的纳秒级全固态脉冲源设计[J]. 强激光与粒子束, 2017, 29:045002 doi: 10.11884/HPLPB201729.160475Li Xiqin, Wu Hongguang, Luan Chongbiao, et al. Design of nanosecond all-solid-state pulse source based on MOSFET semiconductor switch[J]. High Power Laser and Particle Beams, 2017, 29: 045002 doi: 10.11884/HPLPB201729.160475 [5] Wang Liming, Zhang Zhengquan, Liu Qingxiang, et al. A solid-state pulse generator based on multilayer ceramic capacitors and insulated gate bipolar transistors[J]. Review of Scientific Instruments, 2020, 91: 054703. doi: 10.1063/1.5144479 [6] 朱晓光, 张政权, 刘庆想, 等. 脉冲功率应用的IGBT快速驱动电路[J]. 强激光与粒子束, 2018, 30:015001 doi: 10.11884/HPLPB201830.170330Zhu Xiaoguang, Zhang Zhengquan, Liu Qingxiang, et al. High speed IGBT gate driving circuit applied to pulsed power system[J]. High Power Laser and Particle Beams, 2018, 30: 015001 doi: 10.11884/HPLPB201830.170330 [7] 孙瑞泽, 陈万军, 刘超, 等. 压控型脉冲功率半导体器件技术及应用[J]. 强激光与粒子束, 2024, 36:095001 doi: 10.11884/HPLPB202436.240120Sun Ruize, Chen Wanjun, Liu Chao, et al. Technology and application of the voltage-controlled pulse power semiconductor devices[J]. High Power Laser and Particle Beams, 2024, 36: 095001 doi: 10.11884/HPLPB202436.240120 [8] Chen Wanjun, Liu Chao, Tang Xuefeng, et al. Experimentally demonstrate a cathode short MOS-controlled thyristor (CS-MCT) for single or repetitive pulse applications[C]//Proceedings of 2016 28th International Symposium on Power Semiconductor Devices and ICs (ISPSD). 2016: 311-314. [9] 刘超. MOS栅控脉冲功率器件模型与新结构研究[D]. 成都: 电子科技大学, 2020Liu Chao. Novel structure and model of MOS gate pulse power devices[D]. Chengdu: University of Electronic Science and technology, 2020 [10] Wu Feiyu, Zhao Lisheng, Dong Shoulong, et al. Magnetic coupling resonant-based air-isolated module for high voltage pulse generators[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2431-2439. doi: 10.1109/TIE.2022.3165285 [11] Li Zi, Liu Haotian, Jiang Song, et al. A new driving circuit with delay trigger for the solid-state Marx modulators[J]. IEEE Transactions on Plasma Science, 2021, 49(6): 1906-1914. doi: 10.1109/TPS.2021.3077601 [12] Rao Junfeng, Zeng Tong, Jiang Song, et al. Synchronous drive circuit with current limitation for solid-state pulsed power modulators[J]. IET Power Electronics, 2020, 13(1): 60-67. doi: 10.1049/iet-pel.2019.0421 -





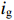
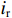
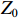
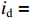
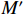
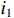
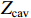
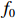
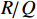

 下载:
下载:
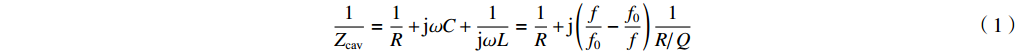
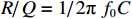
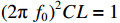
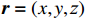
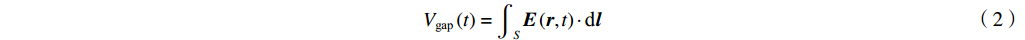
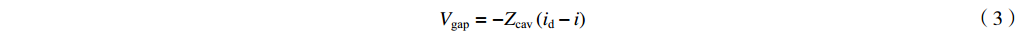
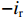
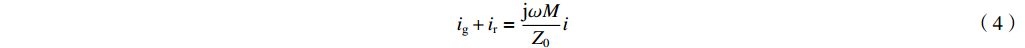
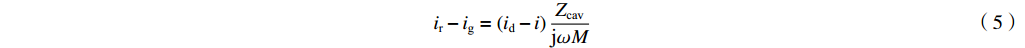
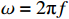


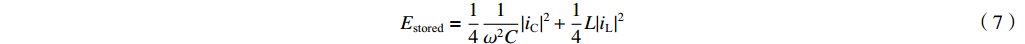
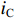
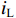
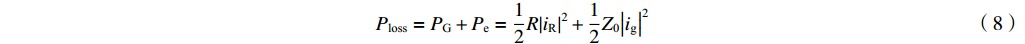
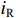
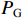
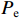
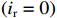
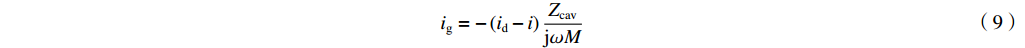
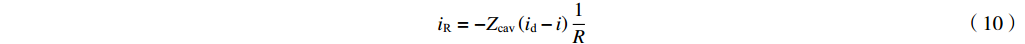
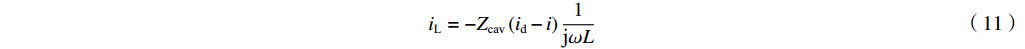
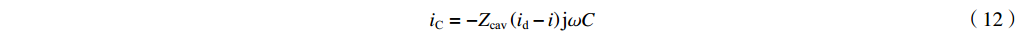
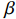
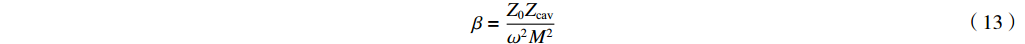
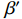
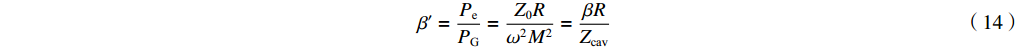
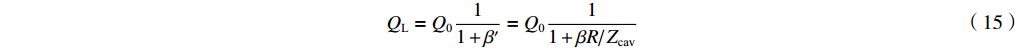
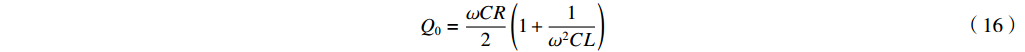
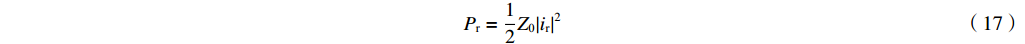
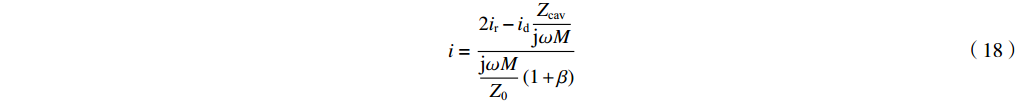
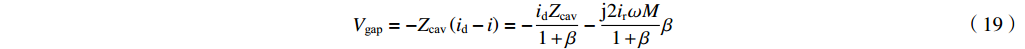
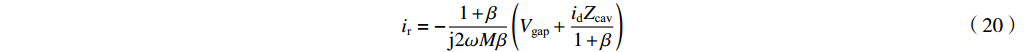
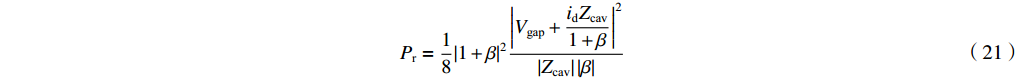
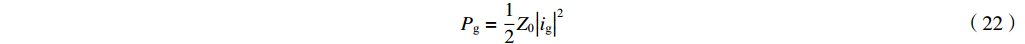
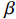
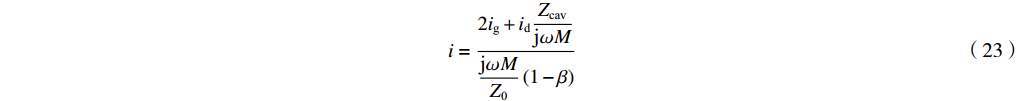
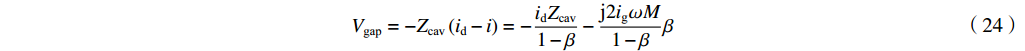
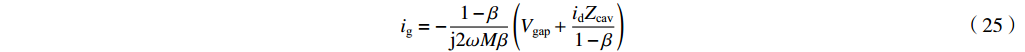
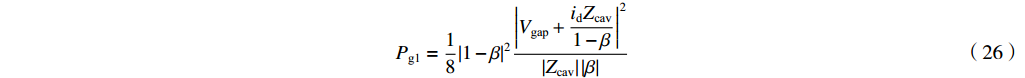
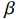
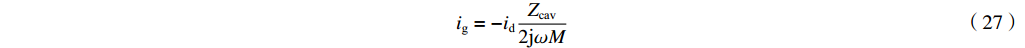
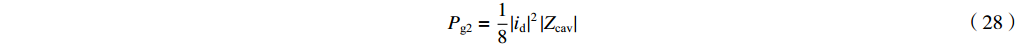
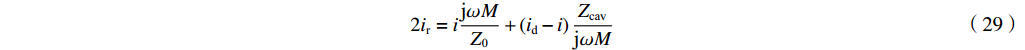
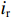
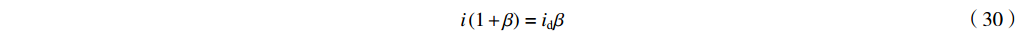
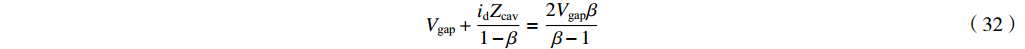
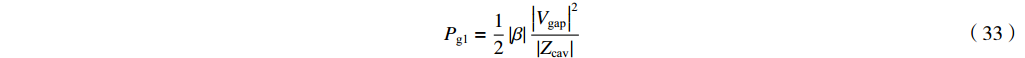
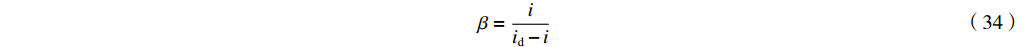
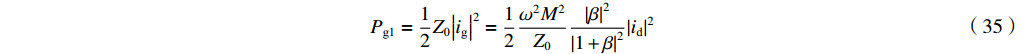
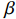
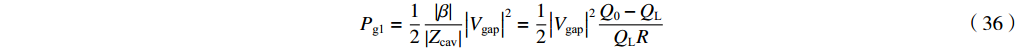
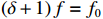
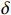
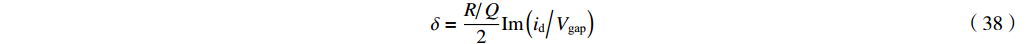
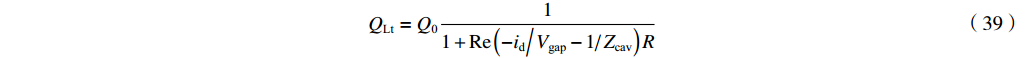
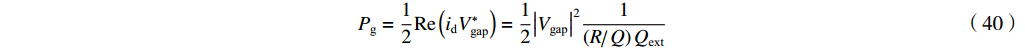
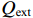
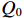
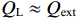
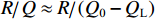
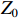
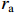
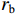
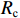
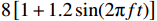
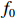
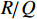
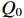
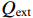

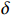


 下载:
下载: