Matching theory and PIC simulation for klystron output cavity with beam
-
摘要: 基于输出波导与腔体耦合的等效电路模型,对于任意的输出波导与腔体的耦合和任意的腔体和电子束参数,建立了速调管放大器输出腔的匹配理论即最大输出功率理论。建立了带有互感和感应电流等参数的输出腔等效电路模型,研究了输出微波功率和反射功率,其中在研究反射功率时讨论了复耦合系数不等于1和等于1这两种情况下反射功率的表达式,推导了输出波导与带有电子束的输出腔任意的耦合和完全匹配这两种情形时输出微波功率和间隙电压关系的公式。推导了完全匹配时输出腔谐振频率与输出腔有载品质因数的表达式。匹配情形时从含有互感的等效电路模型推出的输出功率的计算结果与经典理论的计算结果近似相等。Abstract: The matching theory based on an equivalent circuit model is outlined that self-consistently determines the modulation of a klystron output cavity for arbitrary coupling of the output waveguide to the cavity and arbitrary cavity and/or electron beam parameters. An equivalent circuit model including a mutual inductance and the induced current for the output cavity is established, the output power and the reflected power are discussed. For the cases where the complex coupling coefficient equals 1 and does not equal 1, we respectively determined expressions for the reflected power. We derived an expression for the output power corresponding to the gap voltage for the case when the coupling is perfectly matched to the output waveguide, and also for the case of arbitrary coupling. We worked out expressions for the resonant frequency of the output cavity and externally-loaded Q leading to the matching conditions. If the matching conditions are satisfied, the output power corresponding to the new theory equals approximately the output power corresponding to the traditional theory.
-
高增益[1-3]是速调管放大器一个重要的发展方向,增大输出腔的输出功率是提高增益的一种有效方式。如果反射功率为零,输出波导与输出腔的耦合就达到了匹配状态,输出腔的输出功率就达到了最大值。文献[4]给出了输出腔等效电路和输出功率计算公式。这里的输出腔等效电路采用变压器模型来研究输出腔与输出波导之间的耦合。输出功率计算公式是一种典型的传统算法。这种输出功率的算法得到了广泛的应用,基于圆盘模型的一维粒子模拟软件的输出功率的计算就是采用这种算法。按照传统算法,输出功率与工作频率无关,只与输出腔的间隙电压、特性阻抗和外观品质因数有关。本文提出了新的等效电路和输出功率计算公式[5-6]。输出腔等效电路以感应电流作为激励源,输出腔采用电阻、电容和电感组成并联电路,采用互感模型来研究输出腔与输出波导之间的耦合,采用传输线理论研究输出波导中的入射波和反射波。因为该模型为自洽模型,腔体通过电子束反馈回自身的效应通过感应电流来考虑,所以电子束阻抗在模型中不是必须的。当输出波导中的反射波为零时,带有调制电子束的输出腔与输出波导达到匹配状态。按照匹配理论,在匹配状态时,输出腔的工作频率与输出腔的谐振频率之间存在频率差。频率差是由输出腔的特性阻抗,感应电流和间隙电压决定的,同时还推出了匹配状态下输出腔有载品质因数的计算公式。从传统的输出腔的等效电路模型出发,无法推出完全匹配时输出腔谐振频率与有载品质因数的表达式。本文建立了较完整的带有电子束和输出波导的输出腔匹配理论即最大输出功率理论,推导了输出波导与带有电子束的输出腔之间任意的耦合和完全匹配这两种情形时输出微波功率和间隙电压关系的公式。将匹配情形时从含有互感的等效电路模型推出的输出功率的公式与传统的经典理论的公式进行比较,发现两者近似相等。
这套理论不仅得出了一般情形时输出功率与间隙电压等参量的关系式,而且可以得出匹配情形时(输出波导内反射波为零)的输出功率与间隙电压等参量的关系式,以及匹配情形时的工作频率和输出腔的谐振频率两者之间关系式和有载品质因数的表达式。根据这两个表达式就可以计算出输出腔的谐振频率和外观品质因数,这两个参数可以作为输出腔的设计依据。
1. 腔体模型
图1给出了输出腔的等效电路模型[4-9]。图1中
ig 是在与腔体耦合的输出波导中产生的出射电流,ir 是波导中的反向电流,Z0 是波导特性阻抗,R是腔体并联电阻,L是腔体电感,C是腔体电容,i是腔体电路中流过互感M的电流,id=M′i1 是腔体电路中由于调制电子束而引起的电流,通常被称为感应电流,M′ 是电子束和输出腔之间的耦合系数,i1 是束流的一次谐波。腔体和波导通过互感M互相耦合。输出腔阻抗Zcav 由腔体并联阻抗R,腔体电容C,腔体电感L或者由R、腔体谐振频率f0 、工作频率f和腔体特性阻抗R/RQQ 给出1Zcav=1R+jωC+1jωL=1R+j(ff0−f0f)1R/RQQ (1) 这两种定义通过
R/RQQ=1/12π f02π f0C 和(2π f0)2CL=1 相联系。腔体间隙电压定义为在位置矢量r=(x,y,z) 处腔体射频电场沿着某个感兴趣的路径S瞬时线积分Vgap(t)=∫SE(r,t)⋅dl (2) 腔体间隙电压是图1中腔体阻抗两端的电压,由下式给出
Vgap=−Zcav(id−i) (3) 2. 外耦合模型
这里我们将定义输出腔与外部波导耦合的模型。外部波导中同时存在带有电流ig和电压igZ0的出射波以及电流
−ir 和电压irZ0的反射波。利用图1和互感的定义,我们可以得出腔体-波导电路中电流的表达式ig+ir=jωMZ0i (4) ir−ig=(id−i)ZcavjωM (5) 式中:
ω=2πf 是工作角频率。2.1 有载品质因数Q
首先我们将给出没有电子束和外部微波源关闭时的有载品质因数Q。冷腔有载品质因数定义为
Ql=ωEstoredPloss (6) 式中:
Estored 是腔体中平均储能,表示为Estored=141ω2C|iC|2+14L|iL|2 (7) 式中:
iC 是流过电容器的电流,iL 是流过电感的电流,平均功率损耗为Ploss=PG+Pe=12R|iR|2+12Z0|ig|2 (8) 式中:
iR 是流过腔体电阻的电流,PG 为腔体电阻损耗功率,Pe 为从腔体泄漏到波导中的功率。在无反射波的情形下(ir=0) 有ig=−(id−i)ZcavjωM (9) iR=−Zcav(id−i)1R (10) iL=−Zcav(id−i)1jωL (11) iC=−Zcav(id−i)jωC (12) 我们定义复耦合系数
β 为β=Z0Zcavω2M2 (13) 根据腔体与波导耦合系数
β′ 的定义β′=PePG=Z0Rω2M2=βRZcav (14) 没有电子束的有载品质因数为
QL=Q011+β′=Q011+βR/βRZcavZcav (15) 其中固有品质因数
Q0=ωCR2(1+1ω2CL) (16) 2.2 反射微波功率
反射微波功率为
Pr=12Z0|ir|2 (17) 从式(4)和式(5)中消去出射波,我们可以得到腔内驱动电流为
i=2ir−idZcavjωMjωMZ0(1+β) (18) 这个表达式可以用来推出间隙电压
Vgap=−Zcav(id−i)=−idZcav1+β−j2irωM1+ββ (19) 或者反过来,波导中的反射波为
ir=−1+βj2ωMβ(Vgap+idZcav1+β) (20) 从这个表达式可以导出一般情形时反射微波功率为
Pr=18|1+β|2|Vgap+idZcav1+β|2|Zcav||β| (21) 2.3 输出微波功率
输出微波功率为
Pg=12Z0|ig|2 (22) 下面分两种情形讨论。
1)当复耦合系数
β 不等于1时:从式(4)和式(5)中消去反射波,我们可以得到腔内驱动电流为i=2ig+idZcavjωMjωMZ0(1−β) (23) 这个表达式可以用来推出间隙电压
Vgap=−Zcav(id−i)=−idZcav1−β−j2igωM1−ββ (24) 或者反过来,波导中的出射波为
ig=−1−βj2ωMβ(Vgap+idZcav1−β) (25) 从这个表达式可以导出输出波导中的输出微波功率为
Pg1=18|1−β|2|Vgap+idZcav1−β|2|Zcav||β| (26) 2)当复耦合系数
β 等于1时:从式(4)和式(5)中消去反射波,我们可以得到出射电流为ig=−idZcav2jωM (27) 将式(27)代入式(22)可以导出输出微波功率为
Pg2=18|id|2|Zcav| (28) 3. 匹配耦合的特殊情形
如果输出波导中没有反射波,波导与腔体的耦合就达到了匹配。因为匹配将导致输出微波功率达到最大值,所以波导与腔体的匹配是波导和腔体的设计目标。
3.1 输出微波功率
从式(4)和式(5)得到
2ir=ijωMZ0+(id−i)ZcavjωM (29) 令
ir 为零可以导出i(1+β)=idβ (30) 式(30)为匹配条件。在这种情形下,间隙电压为
Vgap=−Zcavid1+β (31) 或者
Vgap+idZcav1−β=2Vgapββ−1 (32) 与这个条件相对应,匹配时输出微波功率为
Pg1=12|β||Vgap|2|Zcav| (33) 对于匹配条件式(30)必须满足,或者
β=iid−i (34) 匹配时输出微波功率又可以写为
Pg1=12Z0|ig|2=12ω2M2Z0|β|2|1+β|2|id|2 (35) 由
β 的定义式(13)和式(33)与式(15)可得Pg1=12|β||Zcav||Vgap|2=12|Vgap|2Q0−QLQLR (36) 3.2 匹配时的微波频率与有载品质因数
通过比较复耦合系数
β 的定义式(13)和式(31),可以得出ω2M2=Z0−id/−idVgapVgap−1/1ZcavZcav (37) 这个方程等式左边为实数,右边通过工作频率的合适的选择也可以成为实数。定义
(δ+1)f=f0 ,如果δ 满足δ=R/RQQ2Im(id/idVgapVgap) (38) 则式(37)右边成为实数。匹配时有载品质因数为
QLt=Q011+Re(−id/−idVgapVgap−1/1ZcavZcav)R (39) 4. 从含有互感的等效电路模型推出的理论与经典理论的比较
从谐振腔的一般理论[4]可以得出
Pg=12Re(idV∗gap)=12|Vgap|21(R/RQQ)Qext (40) 这里我们把它称为经典理论。对于输出腔来说,
Qext 远小于Q0 ,QL≈Qext ,R/RQQ≈R/R(Q0−QL)(Q0−QL) ,匹配情形时的式(36)与式(40)近似相等。一般情形时的式(26)与式(40)只有通过数值计算进行比较。5. 输出腔的理论计算与粒子模拟的比较
单重入输出腔的2维粒子模拟结构图如图2所示。图2中输出腔外径为5.6 cm,输出同轴线的内外径分别为5.2 cm和5.5 cm,特性阻抗
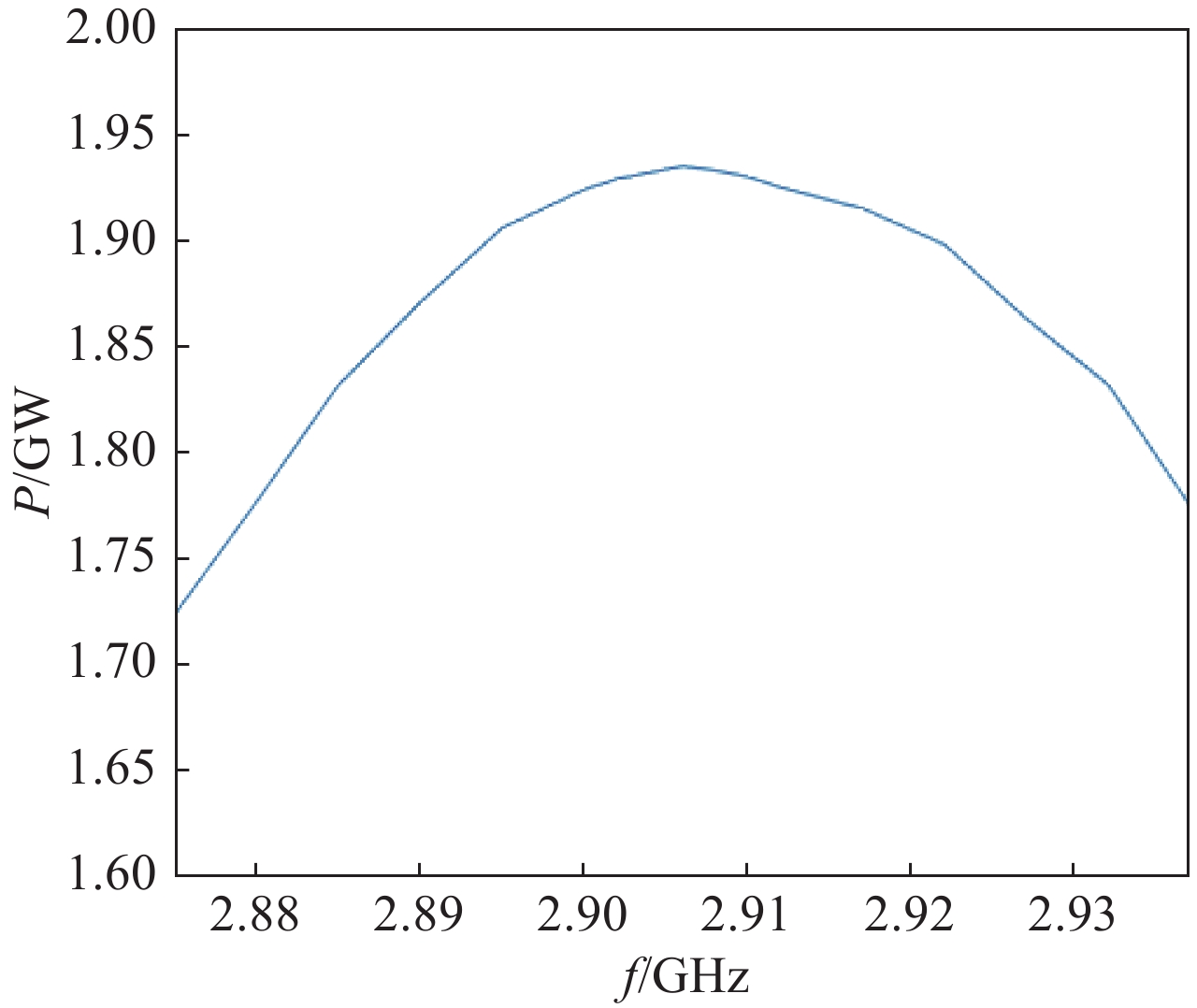
Z0 为3.365 Ω,间隙距离为1.4 cm,ra 和rb 分别等于2.4 cm和2.8 cm,为环形电子束的内半径和外半径,Rc 等于3.0 cm为漂移管半径,鼻锥厚度为6 mm。在粒子模拟中束压为724.4 kV,束流为8[1+1.2sin(2πft)] kA,外加均匀磁场为1.2 T。输入腔谐振频率f0 为2.933 GHz,特性阻抗R/RQQ 为6.727 Ω,固有品质因数Q0 为4 406.7,外观品质因数Qext 为18.8,图1中R为29 643.871 Ω,L为0.365×10−9 H,C为8.07 pF。当基波电流调制系数为1.2时,采用2维粒子模拟计算了输出微波功率与工作频率关系,计算结果如图3所示。从图3可知,当工作频率为2.906 GHz时,输出微波功率达到最大值;输出腔间隙耦合系数为0.635 9,基波电流为−9.6 kA,间隙电压为(6.767×105+2.742×105i) kV,复耦合系数为
3.5276 ×10−2+2.875 3 i,互感为1.1299 ×10−9 H,腔体阻抗为(4.461+3.636×10−2 i)Ω。根据式(38)可以得出δ 为0.010 6,所以匹配时工作频率为2.902 3 GHz,工作频率的理论值与粒子模拟的工作频率相差3.7 MHz。根据式(39)可以得出匹配时有载品质因数理论值为19.18,而粒子模拟的有载品质因数为18.72,两者相差0.46。按照式(21)计算的反射功率为1.5962 MW。按照式(26)计算的输出微波功率为2.058 GW,粒子模拟为1.935 GW,两者相差0.123 GW。按照式(36)计算的输出微波功率为2.107 6 GW。6. 结 论
匹配理论不仅得出了一般情形时输出功率与间隙电压等参量的关系式,而且可以得出匹配情形时(输出波导内反射波为零)的输出功率与间隙电压等参量的关系式,以及匹配情形时的工作频率和输出腔的谐振频率两者之间关系式和有载品质因数的表达式。根据这两个表达式就可以计算出输出腔的谐振频率和外观品质因数,这两个参数可以作为输出腔的设计依据。匹配情形时从含有互感的等效电路模型推出的输出功率的计算结果与经典理论的计算结果近似相等。
-
-
[1] 吴洋. 强流高增益相对论速调管放大器理论和实验研究[D]. 北京: 清华大学, 2013Wu Yang. Theoretical and experiment study on intense beam high gain relativistic klystron amplifier[D]. Beijing: Tsinghua University, 2013 [2] Wu Yang, Xu Zhou, Jin Xiao, et al. A long pulse relativistic klystron amplifier driven by low RF power[J]. IEEE Transactions on Plasma Science, 2012, 40(10): 2762-2766. doi: 10.1109/TPS.2012.2210250 [3] Wu Yankai, Xie H Q, Li Z H, et al. Gigawatt peak power generation in a relativistic klystron amplifier driven by 1 kW seed-power[J]. Physics of Plasmas, 2013, 20: 113102. doi: 10.1063/1.4828975 [4] 丁耀根. 大功率速调管的理论与计算模拟[M]. 北京: 国防工业出版社, 2008: 73-75Ding Yaogen. Theory and computer simulation of high power klystron[M]. Beijing: National Defence Industry Press, 2008: 73-75 [5] 何琥, 李士锋, 刘振帮. 速调管放大器输入腔的匹配理论和模拟研究[J]. 强激光与粒子束, 2024, 36:103004 doi: 10.11884/HPLPB202436.240226He Hu, Li Shifeng, Liu Zhenbang. Matching theory and PIC simulation for klystron input cavity with microwave beam[J]. High Power Laser and Particle Beams, 2024, 36: 103004 doi: 10.11884/HPLPB202436.240226 [6] Carlsten B E, Ferguson P. Numerical determination of the matching conditions and drive characteristics for a klystron input cavity with beam[J]. IEEE Transactions on Electron Devices, 1997, 44(5): 894-900. doi: 10.1109/16.568055 [7] Carlsten B E, Faehl R J, Fazio M V, et al. Beam-cavity interaction physics for mildly relativistic, intense-beam klystron amplifiers[J]. IEEE Transactions on Plasma Science, 1994, 22(5): 730-739. doi: 10.1109/27.338289 [8] Wilsen C B, Luginsland J W, Lau Y Y, et al. A simulation study of beam loading on a cavity[J]. IEEE Transactions on Plasma Science, 2002, 30(3): 1160-1168. doi: 10.1109/TPS.2002.801623 [9] Carlsten B E, Ferguson P, Sprehn D. Accuracy of the equivalent circuit model using a fixed beam impedance for klystron gain cavities[J]. IEEE Transactions on Plasma Science, 1998, 26(6): 1745-1749. doi: 10.1109/27.747895 -





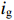
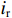
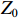
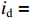
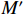
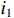
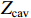
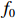
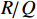

 下载:
下载:
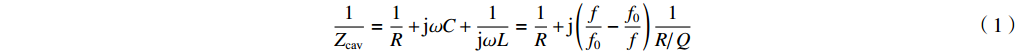
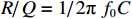
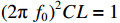
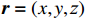
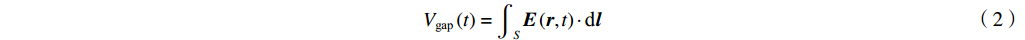
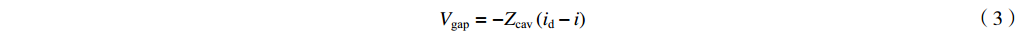
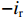
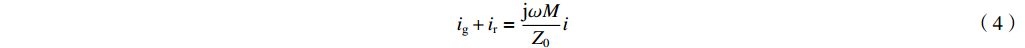
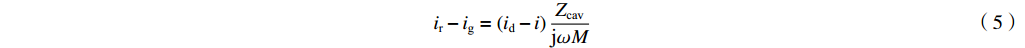


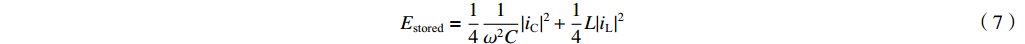
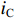
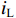
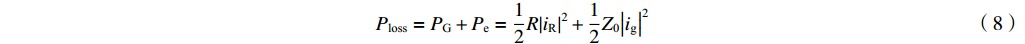
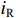
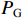
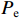
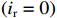
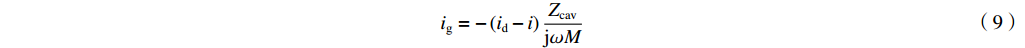
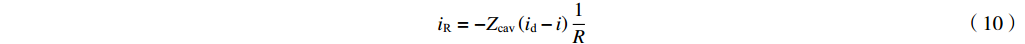
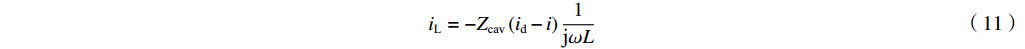
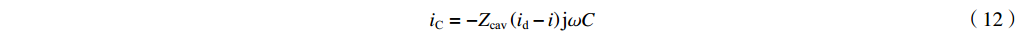
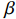
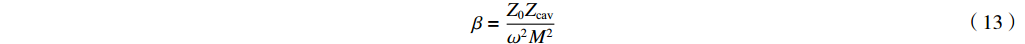
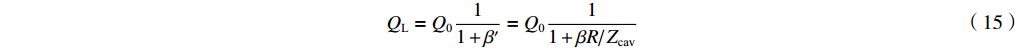
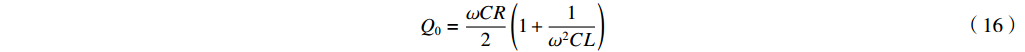
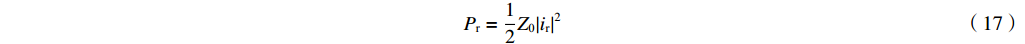
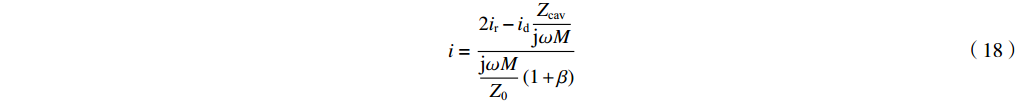
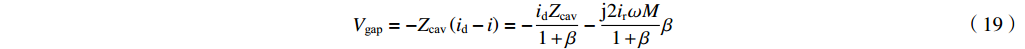
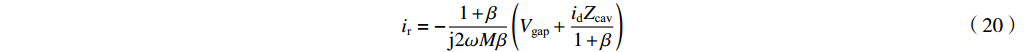
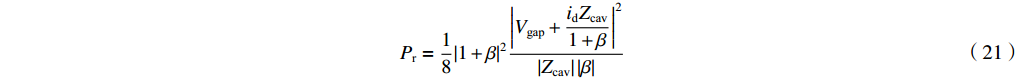
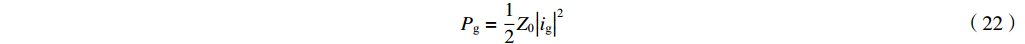
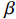
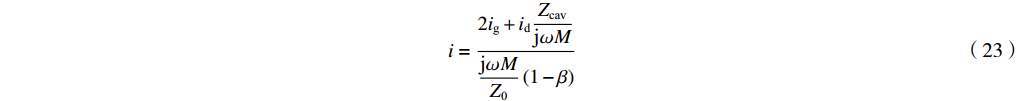
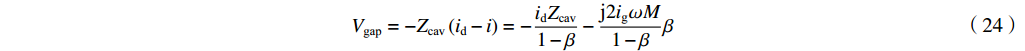
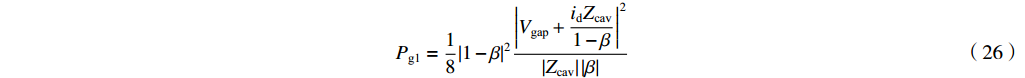
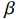
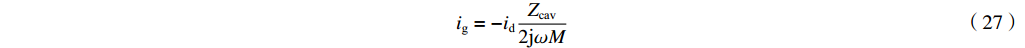
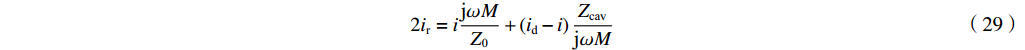
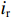
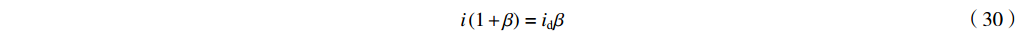
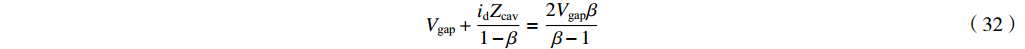
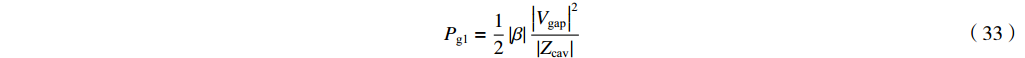
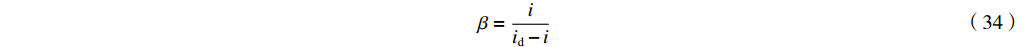
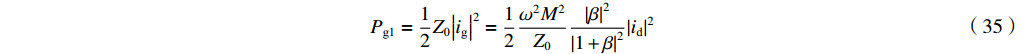
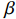
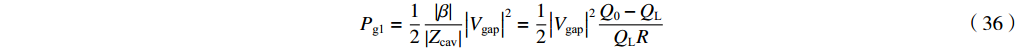
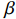
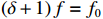
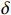
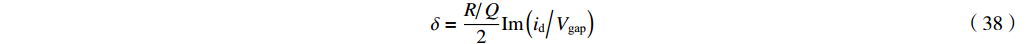
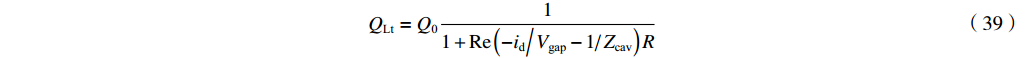
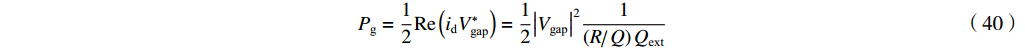
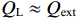
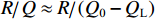
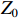
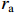
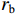
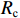
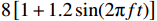
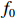
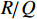
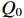
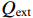

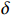


 下载:
下载: