Development of INSL-UniFoam: a multi-physics integrated criticality safety analysis program
-
摘要: 快中子脉冲堆（FBR）是临界安全分析研究的重要对象。它们具有几何形状不规则、强瞬态过程、多物理紧密耦合以及复杂的反馈特性等特点。为了精确模拟并分析快中子脉冲堆在瞬发超临界过程中各物理场的变化情况，开发了一门基于OpenFOAM的多物理核临界安全分析程序，名为INSL-UniFoam。该程序集成了离散纵坐标中子输运求解器、传热和应力-应变求解器，能够模拟快中子脉冲堆的瞬态超临界脉冲过程。程序在Godiva-I基准题中进行了验证，对稳态条件下的多个物理参数进行了敏感性分析。同时，程序还对Godiva-I的瞬态脉冲场景进行了计算并与实验结果进行了比对。结果表明，程序在中子学计算方面具有较高的精度，能精确反映脉冲堆的功率、中子通量的分布情况。同时瞬态耦合计算所得的脉冲功率曲线、峰值功率、裂变产额等方面与参考解符合良好，能够较好地反映脉冲过程并且能够完整地输出脉冲过程的功率、温度、应力应变在内多个物理场的分布情况并与实验结果较好地匹配。Abstract: Fast Burst Reactors (FBRs) are important subjects for criticality safety analysis research. They are characterized by irregular geometry, strong transient processes, tight multi-physics coupling, and complex feedback characteristics. This paper introduces an OpenFOAM based multi-physics nuclear criticality safety analysis code named INSL-UniFoam. It integrates discrete ordinate neutron transport solver, heat transfer and stress-strain solvers to detailly model the prompt super-critical burst pulse of FBRs. The UniFoam is first verified in the Godiva-I benchmark under both the steady-state condition and several transient scenarios. The results demonstrate that the program aligns well with the reference solution in terms of Keff calculation, peak power, and fission yield. Furthermore, it is capable of comprehensively outputting the distributions of power, temperature, and stress-strain throughout the pulse process.
-
压力恢复系统扩压器是化学激光器的重要组成部件之一，位于光学谐振腔与引射器之间，其主要作用是降速增压，将大部分动能转化为压力能，从而提高出口介质的静压，使气体以较小的能量损失进入到引射器系统，同时使得激射腔增益区内的气动流场满足激光器正常运转要求[1-2]。与标准的气动扩压器相比，连续波化学激光器扩压器的本质特点是：扩压器入口雷诺数很低，扩压器壁面有很厚的边界层，入口气流极不均匀[3]。边界层将减小可用于压力恢复的气流动量，同时减小气流流通通道的横截面积，从而导致压力恢复的实际值低于理论值，使得扩压器的扩压效率很低[4]。扩压器的扩压效果直接影响出口介质的静压，进而影响后续尾气排放系统（如引射器和引射气源）的规模大小[5]。因此，在激光器设计和研制中，扩压器的研究具有非常重要的工程应用价值。
目前，针对化学激光器扩压器的研究主要集中在总压损失、抵抗背压能力以及流场对光腔的影响等方面[6-8]。李金雪等提出了通过逐级启动的方式提升扩压器恢复压力[9-11]；余真等对大长高比的扩压器进行了数值模拟研究，获得了高达10左右的扩压器出入口静压比[12]；符澄等关于氧碘化学激光器在光腔与扩压器之间插入一段带二次喉道的部段，提高了扩压器的背压[13]；陈吉明等通过增加边界层吹气的方法提高了扩压器扩压效率[14]。这些研究成果都对进一步提高DF化学激光器扩压器扩压效率提供了非常好的指导作用，但DF化学激光器仍然存在扩压器的出口背压偏低、总压损失较大的问题。近些年，计算流体力学快速发展，已经能够对三维的湍流模型进行比较准确的模拟计算[15]。通过CFD的方法既可以节省硬件加工经济成本，也大大缩短了试验测试的时间成本，并且能够更加精确地了解扩压器优化前后气动流场特性的变化，为优化结构设计提供依据。
本文通过对DF化学激光器的尾气介质在超音速扩压器内的流动进行数值模拟研究，获得不同背压条件下扩张角、结构类型等对扩压器性能的影响，同时根据模拟结果进行了相应的试验验证。
1. 数值模拟
1.1 物理模型及方法验证
扩压器的入口尺寸为140 mm（高）×227 mm（宽），扩压器由超音速平直段和亚音速扩张段两部分组成，主要从亚扩的扩张角和超扩的二次喉道两方面进行研究，探索更加高效的扩压器结构，如图1所示，其中：
（1）无二次喉道的扩压器，只包括平直段和扩张段两部分，其中亚扩的扩张角主要采用了半角8°和半角5°两种结构；
（2）二次喉道的扩压器类型，有收缩段、喉道平直段和扩张段。
本文主要研究上述两种措施对于扩压器性能的改变。扩压器性能研究的项目措施和工作状态较多，这里是对DF激光器尾气在扩压器内的流动进行三维定常数值模拟。
采用压力入口的边界条件，条件为实测的光腔出口的平均参数，其中质量流密度为2.75 g·s−1·cm−2，静压为7.06 kPa，总温为
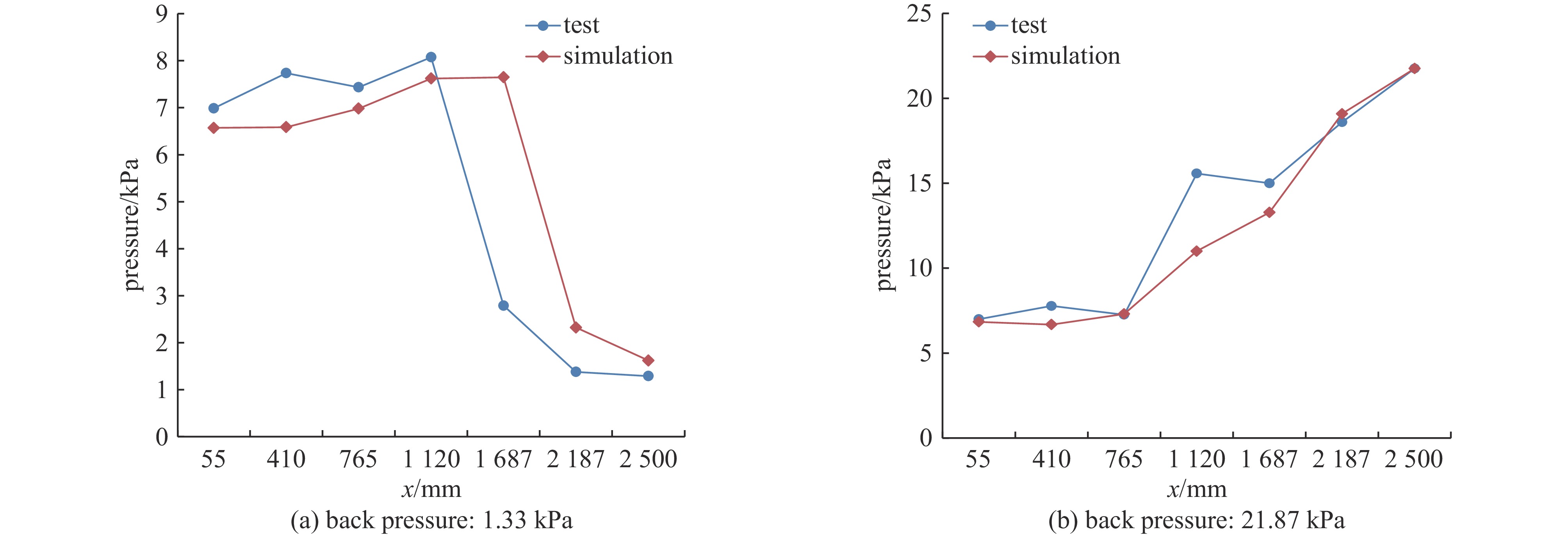
1300 K，介质为DF激光器的激光尾气。出口边界条件设置为压力出口，背压从1.33 kPa的低压开始，确保扩压器的顺利启动，根据扩压器内的激波位置，逐步调高背压。传统DF化学激光器扩压器由平直段和8°角的扩张段组成，通过将数值模拟的结果与试验结果的比较，验证模拟方法的准确性。图2是对不同背压下模拟值和实测值的对比，可以看出模拟计算的数值与实测值存在差异性，尤其是在低压运行时，这主要是因为模拟计算是尾气理想状态的计算结果，而DF化学激光器的试验是经过混合燃烧后的尾气排放的过程，因此两者数值存在一定的差异性，但模拟结果与试验结果整体趋势一致，尤其高背压情况下扩压器启动运行时两者数据比较接近。
图 2 传统型扩压器的计算和实验结果Figure 2. Comparison of numerical and experimental results with traditional diffuser1.2 扩压器扩张角的影响
传统DF化学激光器扩压器由平直段和8°角的扩张段组成，通过数值模拟计算以及试验验证发现传统扩压器抵抗背压的能力有限，因此通过改变扩压器扩张段的扩张角来优化扩压器的性能。图3给出了传统的亚扩段扩张角为8°、背压为23.34 kPa和24.53 kPa条件下的扩压器内马赫数分布，可以看出，23.34 kPa的背压条件下，超音速区域在扩压器内部占据很少的部分，扩压器入口不远处就出现堵塞的现象，边界层出现分离，并在分离处出现强激波；而24.53 kPa背压下马赫数已全程小于1，从表1也可以看出背压至24.53 kPa，扩压器距离入口25 mm处的压力高达10.71 kPa，该值已经远远超过了入口的条件，激波已进入光腔内，直接影响光腔内流场的均匀性，无法满足正常出光条件。因此传统类型的扩压器，抵抗背压的能力相对较低。
表 1 8°扩张角的扩压器静压分布Table 1. Static pressure distribution along the length of diffuser with 8° expansionx/mm static pressure under 23.34 kPa back pressure/kPa static pressure under 24.53 kPa back pressure/kPa 25 7.08 10.71 250 8.59 16.25 500 18.88 19.05 750 19.15 20.03 1200 19.15 21.64 1800 23.24 23.8 从马赫数分布图可以看出亚扩段的中心流与两侧的流动较为明显地产生了分离，这与激波的发展过程也是匹配的。尽管扩压器气流的流动过程是定常流动，但在流动发展初期阶段，激波最先在扩压器的出口出现第一道激波，由于激波和边界层的相互作用使得激波逐渐向上游移动，导致边界层分离，且逐渐波及波前边界层分离，激波串前的马赫数逐步降低，直至整个流场趋于定常。流动中扩压器的扩张角越大流动更加不稳定、不对称，边界层的分离更加严重，激波将会更加容易移出扩压器。
图4是亚扩段5°扩张角，背压在23.34 kPa和26.67 kPa条件下扩压器内的马赫数分布。结合图4和表2可发现在23.3 kPa背压条件下，5°扩张角扩压器的平直段内超音速区域仍然占据主要地位，距离入口750 mm内静压值较低，仍热有较大的空间提升背压，背压提升至26.67 kPa，可以明显看出激波已经接近入口，距离入口250 mm处的静压已达到12.03 kPa但并未影响到扩压器入口压力，因此缩小扩张角时可以明显提高扩压器的恢复压力。
表 2 5°扩张角的扩压器静压分布Table 2. Static pressure distribution along the length of diffuser with 5° expansionx/mm static pressure under 23.34 kPa back pressure/kPa static pressure under 26.67 kPa back pressure/kPa 25 7.07 7.07 250 7.93 12.03 500 8.53 18.13 750 10.2 20.76 1200 16.36 21.77 1800 19.56 24.29 2200 21.99 25.87 2500 22.85 26.64 1.3 二次喉道
扩压器的二次喉道是指超扩的结构形式，对于无二次喉道结构的扩压器，超高速气流经过超声速扩压器，产生激波，压强损失较为严重；带有二次喉道结构的扩压器，超音速气流在通过收缩段减速增压，在二次喉道处马赫数略大于1，然后通过扩张段继续减速增压。二次喉道的速度要低于激射腔出口的速度，经过激波串之后的总压损失较小。反压较小时，二次喉道内皆为超声速气流，随着反压的增大激波串向前移动，当二次喉道内的流动处于亚临界状态时，此时反压或者来流的变化都会轻易使激射腔内的流场发生激烈的变化，不再适宜进行试验。
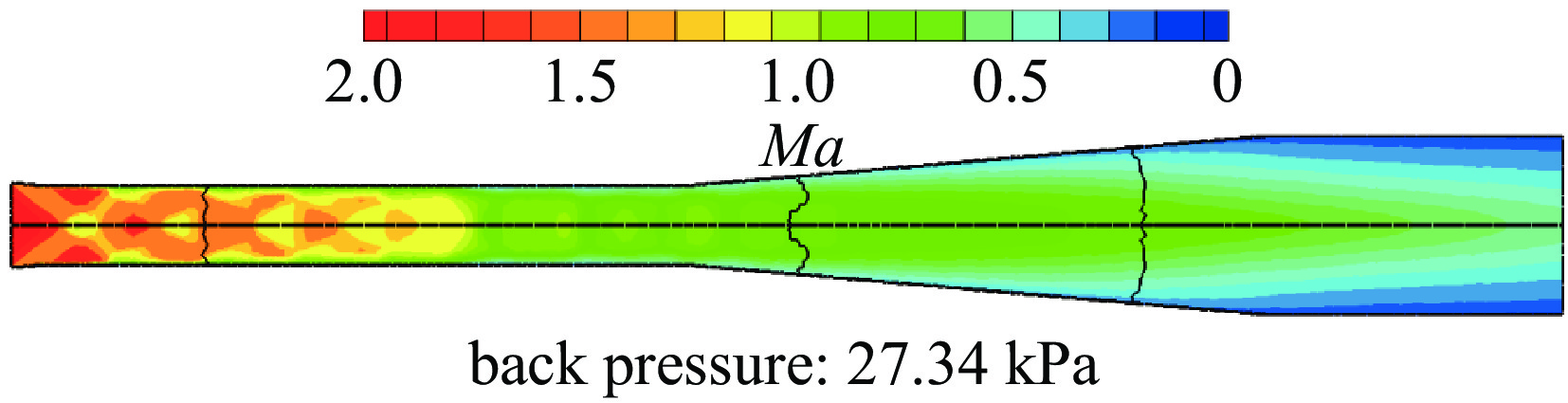
在亚声速扩压段扩张角优化基础上，针对超声速扩压段设计为二次喉道结构进行了数值模拟。图5是二次喉道沿高度方向收缩的扩压器马赫数云图，其中高度方向收缩比为1.08，经计算收缩比进一步增大，激光器无法启动，此时最大背压为27.34 kPa，与无二次喉道相比恢复压力提升仅2%（26.7 kPa→27.34 kPa）。图6为扩压器宽度方向上设计二次喉道的马赫数云图，其中收缩比为1.03，背压分别为27.34 kPa和30.67 kPa，结果显示背压最高可达30.67 kPa，恢复压力可提升14%（26.7 kPa→30.67 kPa），可以看出宽度方向的收缩更有利于扩压器恢复压力的提高，这是由于宽高比较大时，激波在管道内的传播会更加复杂并且出现频繁的反射和绕射，造成激波衰减过快，给恢复压力带来了负面影响。
图 5 沿高度方向二次喉道扩压器的马赫数分布云图Figure 5. Mach number contour of diffuser with secondary-throat along the height direction
图 6 沿宽度方向二次喉道扩压器的马赫数分布云图Figure 6. Mach number contour of diffuser with secondary-throat along the width direction2. 试验研究
设计研制了一套高腔压运转的高恢复压力DF激光器实验室样机。尾气排放子系统包括超音速扩压器、亚音速扩压器以及连接到真空球罐的真空连接通道。在亚音速扩压器下游与真空蝶阀之间安装了自研的电机驱动、连续可调型闸板阀，通过电机驱动调节该阀开启度，能够对增益发生器运转的背压条件进行连续的精细调节，便于恢复压力的测定。
从气动力学角度而言，通常是将激光器能够维持正常运转时，亚音速扩压器出口总压定义为激光器尾气的恢复压力。但由于该截面上的总压分布并不均匀，因此，采用了背压试验来测定实际的平均恢复压力。将背压由低向高逐步提升，直至激波将要进入增益区，从而影响激光器的正常运行。一般认为，能够满足输出功率和激射腔压力基本不变，得到的最大的背压值即为激光器尾气的恢复压力。
试验是采用多种扩压器试验件与同一个增益发生器连接，各种类型扩压器的试验与数值计算都给定了相同的质量流量，尽量保证流动工况的一致性，但因为压力恢复系统扩压器的实际气流流动是一个极其复杂的流动过程，同时采用的闸板阀调压方式与实际背压条件也存在差距，因此理想的计算模型所得具体数值与试验所测的值会有一定的差别，但仍然可以验证措施的有效性。在与数值模拟相同的条件下，通过闸板阀的开启度调节背压，在不同背压的条件下做了多组出光试验。表3是在8°扩张角的扩压器类型下进行的背压试验测量的激射腔压力，激射腔入口压力维持在4 kPa左右时可以保证稳定的激光输出，因此在不影响激射腔压力的前提下，背压可以不断提高。
表 3 背压试验Table 3. Back pressure testsback pressure/kPa pressure of laser cavity/kPa x=24 mm x=98 mm x=138 mm 1.36 4.17 5.75 7.01 13.19 4.04 5.33 6.65 17.08 4.03 5.6 7 20.63 4.13 5.71 6.96 21.8 4 5.48 6.72 2.1 扩张角
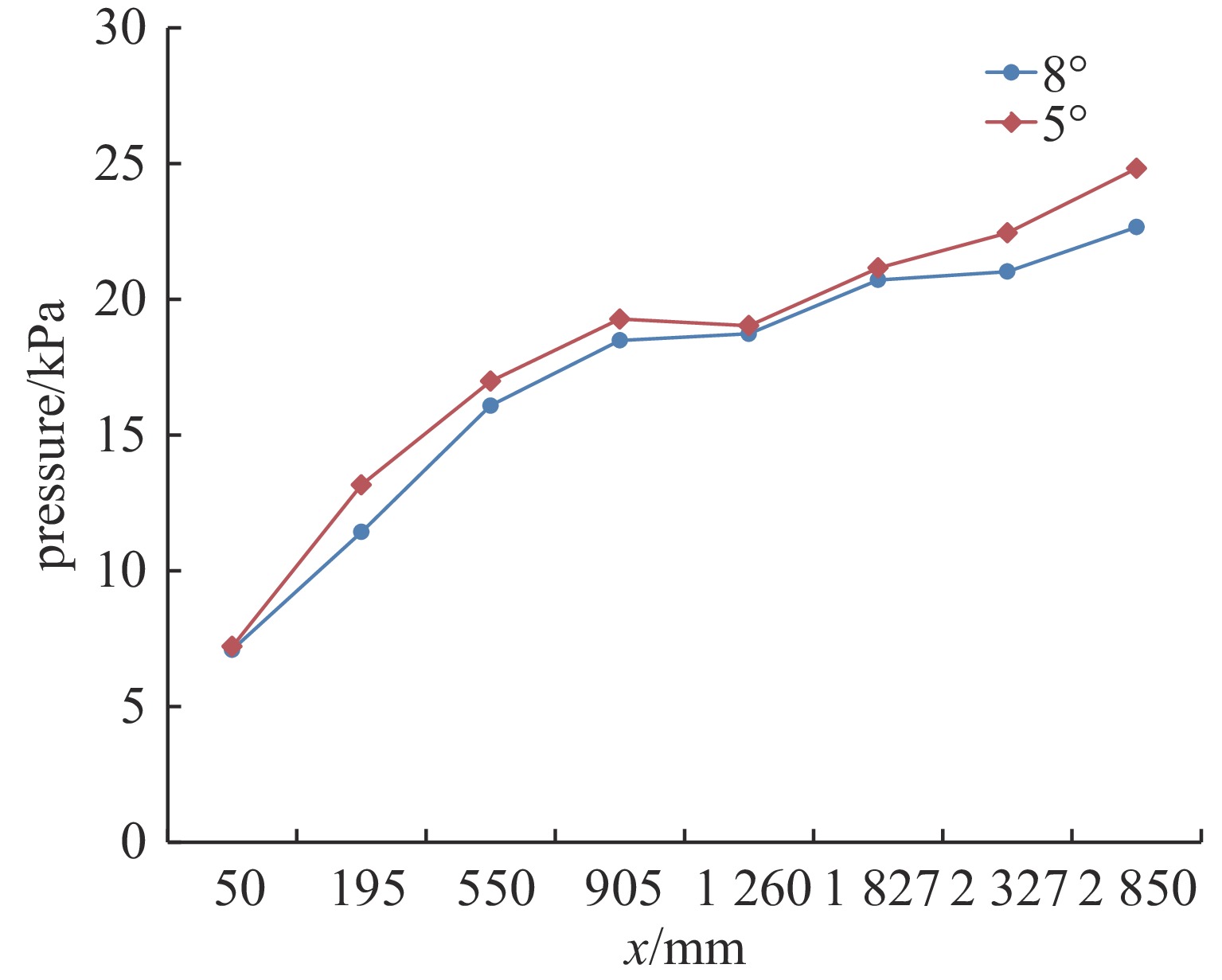
图7是不同扩张角扩压器上壁面的静压值，试验是在保证激射腔压力不变的情况下，最高背压下所测得的扩压器上壁面的压力，明显可以看出5°扩张角的扩压器相比8°的最高恢复压力从22.67 kPa提升至24.8 kPa，与数值计算结果的趋势较一致。试验结果进一步说明扩压器扩张角取较小值时，同样背压下激波位置与超声速区域都较长，抵抗背压能力较强。
2.2 二次喉道
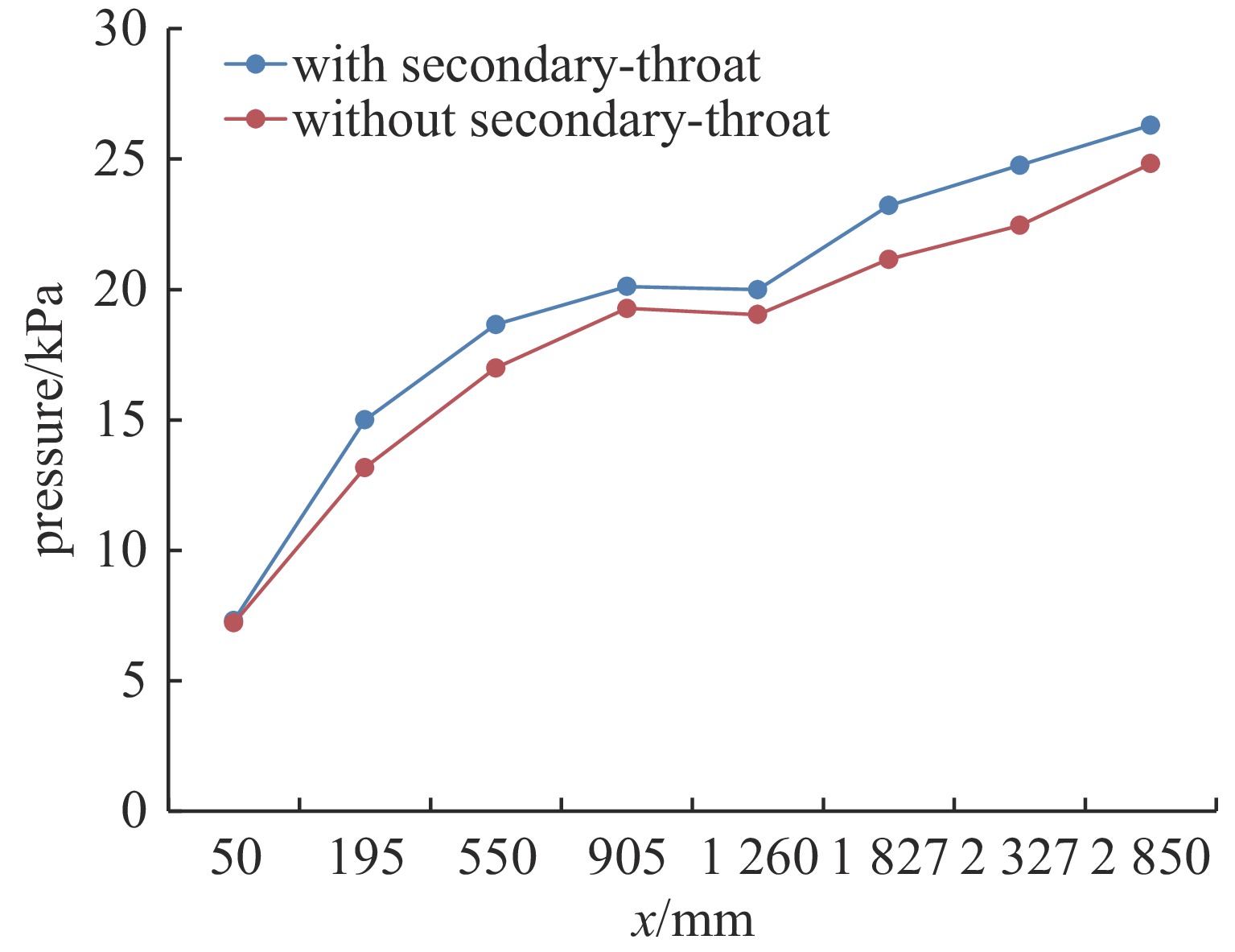
图8是有无二次喉道结构的压力对比，在扩张角优化的基础上，即扩张角为5°；二次喉道数值参考数值模拟的结果，即宽度方向收缩比1.03。试验结果显示二次喉道的结构背压最高能提高到26.27 kPa，明显优于无二次喉道的24.53 kPa。
图 8 有无二次喉道的试验结果对比Figure 8. Comparison of test results with and without secondary-throat3. 结 语
本文采用数值模拟和试验相结合的方法对扩压器压力恢复的流场特性展开研究，并通过对扩压器的优化设计提高了扩压器抗反压能力。通过对DF激光器扩压器内流动的数值模拟和试验结果，可以得出压力恢复系统扩压器性能的一些初步结论：扩压器扩张角的大小对其恢复压力的影响很大，对于DF化学激光器的尾气介质，扩压器具有适当小的扩张角时，在相同的背压条件下具有更长的超声速区，抗反压能力更强。扩压器增加了二次喉道后，压损的减少会降低，能够进一步提高抵抗背压的能力，二次喉道不同的收缩方向效果不同，横截面的长宽比较小时，效果会更好。
-
图 4 29.5 μs初始反应堆周期下反应堆功率随时间变化情况
Figure 4. Total reactor power over time with initial reactor periods of 29.5 μs
图 5 反应堆平均温度以及平均体积膨胀率随时间变化情况
Figure 5. Changes in average temperature and average volume expansion rate of the reactor over time
图 6 功率最大点的功率场分布情况以及脉冲峰结束后的应力分布情况
Figure 6. Distribution of power field at the point of maximum power and the stress distribution after the pulse peak
表 1 不同散射阶数下keff计算结果
Table 1. Calculated keff of Godiva-I in different orders of scattering matrices
scattering matrix keff error/10−5 OpenMC 0.99456 − P0 1.09455 10003 P1 0.97971 1487 P3 0.98583 869 
下载: 导出CSV
表 2 不同网格下的keff计算结果
Table 2. Calculated keff in different meshes
meshing tool cell number keff error/10−5 OpenMC − 0.99456 − blockMesh 56000 0.99272 184 Gmsh 60187 0.99971 515 384803 0.99529 73
下载: 导出CSV
表 3 不同能群数量对应的能量网格划分
Table 3. Energy grids of different energy group structures
33 group energy grid/MeV 8 group energy grid/MeV 1.964033E+01 1.831564E-01 2.034684E-03 2.260329E-05 1.00E+01 1.000000E+01 1.110900E-01 1.234098E-03 1.370959E-05 8.21E-01 6.065307E+00 6.737947E-02 7.485183E-04 8.315287E-06 5.53E-03 3.678794E+00 4.086771E-02 4.539993E-04 4.000000E-06 4.00E-06 2.231302E+00 2.478752E-02 3.043248E-04 5.400000E-07 6.25E-07 1.353353E+00 1.503439E-02 1.486254E-04 1.000000E-07 2.80E-07 8.208500E-01 9.118820E-03 9.166088E-05 1.000010E-11 1.40E-07 4.978707E-01 5.530844E-03 6.790405E-05 5.80E-08 3.019738E-01 3.354626E-03 4.016900E-05 1.00E-11
下载: 导出CSV
表 4 不同能群数量下keff计算结果
Table 4. Calculated keff in different energy groups
energy group number keff Error/10−5 OpenMC 0.99456 − 1 0.95974 3482 8 0.99282 174 33 0.99377 79
下载: 导出CSV
表 5 选取不同求积组的keff计算结果
Table 5. Calculated keff in different quadrature sets
quadrature set keff error/10−5 OpenMC 0.99456 − S2 0.94014 5442 S4 0.99272 184 S8 0.99282 174
下载: 导出CSV
表 6 热应力求解使用的物性参数
Table 6. Thermo-mechanical parameters of Godiva-I
density/
(kg·m−3)Poisson’s
ratio/GPaYoung’s
modulusspecific heat
capacity/(J·kg−1·K−1)thermal conductivity/
(W·m−1·K−1)coefficient of linear
expansion/K−118740 0.23 208 117.7 27.5 1.39$ \times $10−5
下载: 导出CSV
表 7 进一步对比时热应力求解使用的物性参数
Table 7. Additional thermo-mechanical parameters of Godiva-I
peak power/W full width at half maximum/s INSL-UniFoam 7.397E+8 8.4E-5 experiment result 8.223E+8 11.1E-5
下载: 导出CSV
-
[1] Kadioglu S Y, Knoll D A, De Oliveira C. Multiphysics analysis of spherical fast burst reactors[J]. Nuclear Science and Engineering, 2009, 163(2): 132-143. doi: 10.13182/NSE09-07 [2] Briggs J B, Scott L, Nouri A. The international criticality safety benchmark evaluation project[J]. Nuclear Science and Engineering, 2003, 145(1): 1-10. doi: 10.13182/NSE03-14 [3] Wimett T F. Los Alamos: Los Alamos Scientific Lab, 1965. [4] Aufiero M, Fiorina C, Laureau A, et al. Serpent–OpenFOAM coupling in transient mode: simulation of a Godiva prompt critical burst[C]//Proceedings of Joint International Conference on Mathematics and Computation (M&C), Supercomputing in Nuclear Applications (SNA) and the Monte Carlo (MC) Method. 2015. [5] Wilson S C, Biegalski S R, Coats R L. Computational modeling of coupled thermomechanical and neutron transport behavior in a Godiva-like nuclear assembly[J]. Nuclear science and engineering, 2007, 157(3): 344-353. doi: 10.13182/NSE06-28 [6] 高辉, 钟力晗, 梁文峰, 等. 基于反应性温度系数的金属型脉冲堆波形计算[J]. 原子能科学技术, 2017, 51(5):798-802 doi: 10.7538/yzk.2017.51.05.0798Gao Hui, Zhong Lihan, Liang Wenfeng, et al. Waveform calculation of metal burst reactors based on reactivity temperature coefficient[J]. Atomic Energy Science and Technology, 2017, 51(5): 798-802 doi: 10.7538/yzk.2017.51.05.0798 [7] Fiorina C, Aufiero M, Pelloni S, et al. A time-dependent solver for coupled neutron-transport thermal-mechanics calculations and simulation of a Godiva prompt-critical burst[C]//Proceedings of the 2014 22nd International Conference on Nuclear Engineering. 2014. [8] 郭树伟, 陈珍平, 江新标, 等. 金属核燃料快中子脉冲堆核-热-力耦合计算方法研究[J]. 核动力工程, 2022, 43(4):31-37Guo Shuwei, Chen Zhenping, Jiang Xinbiao, et al. Study on neutronic/thermal-mechanical coupling calculation method for fast-neutron pulse reactor with metallic nuclear fuel[J]. Nuclear Power Engineering, 2022, 43(4): 31-37 [9] Wang Lipeng, Guo Shuwei, Hu Tianliang, et al. Transient simulation and parameter sensitivity analysis of Godiva experiment based on MOOSE platform[J]. Energies, 2023, 16(18): 6575. doi: 10.3390/en16186575 [10] Blanco J A. Neutronic, thermohydraulic and thermomechanical coupling for the modeling of criticality accidents in nuclear systems[D]. Grenoble: Université Grenoble Alpes, 2020. [11] 杨波. 离散纵标法求解含有各向异性散射的输运方程[D]. 绵阳: 中国工程物理研究院, 2005Yang Bo. Solution of transport equations with anisotropic scattering using the discrete ordinates method[D]. Mianyang: China Academy of Engineering Physics, 2005 [12] Jasak H, Jemcov A, Tuković Z. OpenFOAM: a C++ library for complex physics simulations[C]//Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics. 2007. [13] Eymard R, Gallouët T, Herbin R. Finite volume methods[J]. Handbook of Numerical Analysis, 2000, 7: 713-1018. [14] Peterson R, Newby G. Lady Godiva: an unreflected uranium-235 critical assembly[R]. Los Alamos: Los Alamos National Lab, 1953. [15] Geuzaine C, Remacle J F. Gmsh: a 3-D finite element mesh generator with built-in pre-and post-processing facilities[J]. International Journal for Numerical Methods in Engineering, 2009, 79(11): 1309-1331. doi: 10.1002/nme.2579 [16] Wimett T, Engle L, Graves G, et al. Time behavior of Godiva through prompt critical[R]. Los Alamos: Los Alamos Scientific Lab, 1956. [17] 张驰, 周琦, 朱庆福, 等. 金属核燃料系统瞬态特性分析研究[J]. 原子能科学技术, 2016, 50(12):2170-2174 doi: 10.7538/yzk.2016.50.12.2170Zhang Chi, Zhou Qi, Zhu Qingfu, et al. Transient characteristic analysis of nuclear metallic fuel system[J]. Atomic Energy Science and Technology, 2016, 50(12): 2170-2174 doi: 10.7538/yzk.2016.50.12.2170 -
下载:
点击查看大图
计量
- 文章访问数: 138
- HTML全文浏览量: 63
- PDF下载量: 9
- 被引次数: 0
