激光自1960年产生以来，便得到了迅速的发展和广泛的使用。在工程领域，金属材料的焊接^[1-2]、切割、熔覆^[3-8]等都离不开激光。激光与金属材料相互作用过程中，金属材料吸收的光能转化为热能，导致金属材料的温度升高。激光加工具有作用时间短、温度变化速度快等特点，除此之外，激光所产生的温度与金属材料的材质有关。因此，研究激光作用于金属材料产生的瞬态温度场分布和激光的中心温度对激光加工有十分重要的意义。目前，已经有诸多的实验与理论工作，例如：毕娟等^[9]利用二维轴对称的物理模型，采用有限元方法模拟了双层材料的瞬态温度场，通过数值模拟计算了激光的瞬态温度场；周杰等^[10]基于脉冲激光辐照金属材料的热学模型，通过热传导方程实现了对激光辐照下瞬态温度场的预测。激光的中心温度的测量一直是一个重要而困难的问题，到目前为止仍没有得到很好的解决。本文利用XL-800WF光纤传输多功能脉冲激光加工系统，在输入电流为150 A、脉冲宽度为2.5 ms的情况下，照射一块较大面积的厚钢板，拍摄了钢板的凝固显微照片。通过建立无热源的热传导方程，研究理想情况下激光中心的温度场，模拟了激光温度场的分布图，推导了激光中心温度的数值范围，并对可能存在的误差进行了分析。

1.   实验

实验上，采用XL-800WF光纤传输多功能脉冲激光加工系统。其最大输出功率800 W，激光波长1064 nm，有效光斑尺寸约1.0 mm，单脉冲最大激光能量90 J，脉冲宽度0.5~5 ms，脉冲频率1~40 Hz。采用光纤传输，聚焦透镜的焦距为160 mm，输入电流为150 A，脉冲持续时间为2.5 ms，设备配置了CCD监视系统。实验使用的钢板表面光洁、平整，表面积足够大，热扩散效果良好。钢板较厚，在激光照射过程中不会熔穿。激光对钢板的一个固定点进行照射，凝固后形成激光熔斑。清除熔斑周围的残渣，拍摄其显微图片。图 1 (a), (b), (c)分别为激光照射1, 2, 3个脉冲的熔斑显微图。由图可以获得清晰的液态钢流动路径。测量结果表明，单次脉冲照射和多次脉冲照射得到的凝固图极为相似，凝固圆的外直径也相同。由此可知，激光器输出稳定，激光每一次照射均具有相同的能量，实验数据可靠。

图  1  激光脉冲分别照射1, 2, 3次的显微图

Figure  1.  Micrographs of laser pulses illuminating 1, 2, 3 times, respectively

下载: 全尺寸图片 幻灯片

2.   瞬态温度场模拟

由于照射的钢板较大，不影响激光热量的扩散。在数学上可以认为是自由边界。以激光熔斑中心为原点建立直角坐标系，r表示任意点的位置，激光作用结束的瞬间为初始时刻。理想情况的热传导方程可写为

式中：u(r, t)表示任意位置、任意时刻的温度；t表示时间；a为热扩散系数；ϕ(r)是初始时刻的温度分布。对方程(1)、(2)进行傅里叶变换，得

式中：U(ω, t)为u(r, t)作傅里叶变换的对应表达式；ω为r的对应算符。其中方程(4)中的Φ(ω)为

式中：ϕ(r)为积分核。联合方程(3)~(4)，解得

将方程(6)作傅里叶逆变换，得

将方程(5)代入方程(7)，得

式中：ζ为积分变量。将方程(8)进一步化简，得

方程(9)是一个卷积形式，利用卷积性质将其写成如下形式

式中: $K(r, t)=\frac{1}{2 a \sqrt{{\rm{ \mathsf{ π}}} t}} \mathrm{e}^{-\frac{r^2}{4 a^2 t}}$。实验使用的XL-800WF光纤传输脉冲激光加工系统，其输出光束为高斯型光束。由于光束的线度远小于光热的影响范围，故用δ函数来表示，即ϕ(r)=δ(r)。因此，计算方程(9)得

方程(11)即为理想情况下激光的中心温度演化函数。结合光与物质相互作用的反应时间和激光熔斑的凝固时间，即可推导、模拟出激光的中心温度。

3.   理论分析

测量光与物质相互作用的反应时间和激光熔斑的凝固时间对瞬态温度场的模拟有重要影响，亦是解决瞬态温度场问题的核心所在。尽管这方面已经有诸多的工作^[11-14], 但仍然没有形成统一的认识和标准。目前，反应时间及凝固时间的获取较为成熟的方法有高速摄像^[15-16]、数值模拟^[17-18]等。其中高速摄像技术获得的数值更为精确，但其设备昂贵，对实验室的要求较高。相对而言，数值模拟更具通用性和实用性。本实验无法实现直接测量，反应时间和凝固时间均通过间接方法得到。同时，本文给出了一个简单且合理的推断，以证明数据的合理性。

反应时间是激光作用于金属材料后，光与物质相互作用需要一个转换时间，使得激光的能量为金属材料吸收并产生热量，转化为金属材料的温度场。通过参考相关的数据，并结合多年的实验经验，反应时间取t=1.0 ms。凝固时间是指金属获得自身的温度场后，熔化为液态，从液态凝固至固态的时间。凝固时间取Δt=0.8 ms。另外，为了说明凝固时间的合理性，凝固时间可以通过白光干涉仪的测量结果及金属的流速来模拟解决。

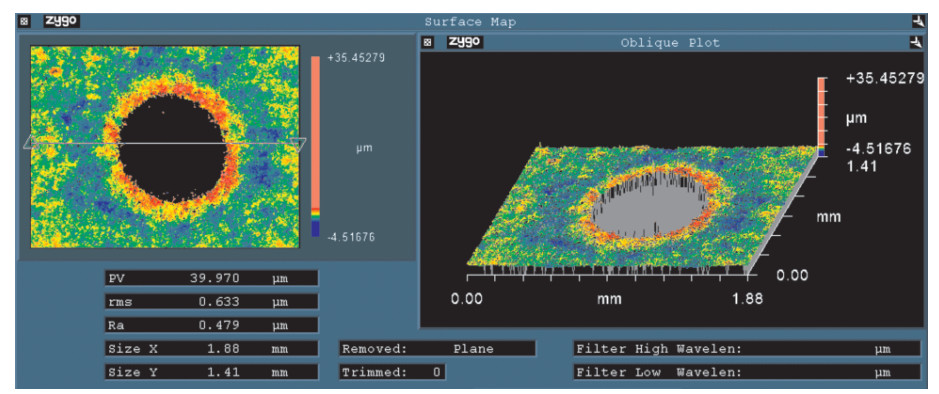
用白光干涉仪测量熔斑的外半径，测量的结果为r=0.4 mm(图 2)。液态钢的流速^[19]一般可以取为v=1.0 m/s。由于凝固时液态金属的粘滞阻力不断增加，流速会逐渐变缓，是一个减速过程，可以用匀减速过程来模拟液态钢的流动，由此可得平均速度为v=0.5 m/s。因此，可计算激光熔斑的凝固时间为

图  2  白光干涉仪测量激光熔斑的半径

Figure  2.  Radius of laser welding spots measured by white light interferometer

下载: 全尺寸图片 幻灯片

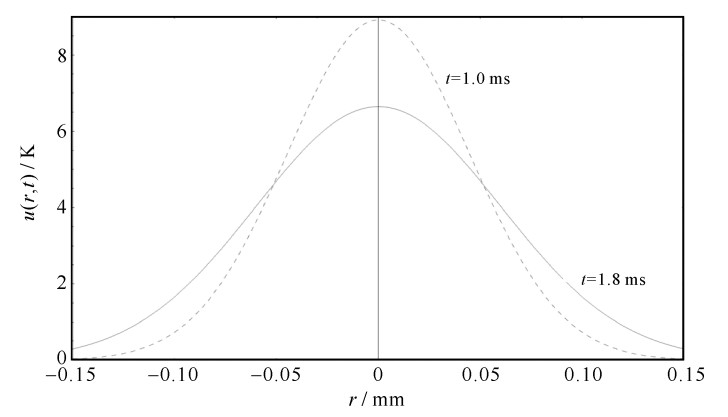
由以上分析模拟可知，钢板的反应时间为t=1.0 ms。激光熔斑从液态转变为固态的凝固的时间为0.8 ms, 整个过程在1.8 ms时刻完成(如图 3所示)。

图  3  钢板的瞬态温度图。其中t=1.0 ms为熔化时的温度，t=1.8 ms为凝固时的温度

Figure  3.  Transient temperature diagram of steel plate. Where t=1.0 ms corresponds to temperature of melting time, t=1.8 ms corresponds to temperature of solidification

下载: 全尺寸图片 幻灯片

将时间t=1.0 ms和t=1.8 ms代入方程(11)，其比值即为凝固时间内激光中心温度的衰减率

方程(13)表明，在0.8 ms内，激光的中心温度减为原来的70.74%。最后，通过纯钢熔点(凝固温度)逆推激光的中心温度。钢的熔点(凝固温度)为1811 K^[20]。由此可以推导激光的中心瞬时温度为

激光作用于金属材料瞬态温度场模拟的类似工作有很多。王馨露^[11]利用非线性瞬态热传导微分方程来模拟激光打孔温度场，并利用ABAQUS有限元分析方法进行计算，得到的结果与本文相吻合。本质上，自由热传导方程与非线性瞬态热传导微分方程对温度场的描述具有一致性。相比之下，非线性瞬态热传导微分方程侧重于金属材料的性质，而自由热传导方程的侧重点在激光加工系统；裴旭等人^[21]采用COMSOL系统研究了脉冲激光与金属铝相互作用时的瞬态温度场变化，得到了瞬态温度分布亦在同一范围内。

长期以来，研究者们在激光中心瞬态温度场和激光的中心温度探测方面做了大量工作，根据实验、经验和模拟方法得到了部分数据。将上述结果与已有的工作经过对比，本文得到的数据与以前的结果比较吻合，得到的数据在同一个温度范围。这也充分表明本文模拟方案较为可靠。

4.   结论

激光的中心温度的测量一直是一个重要而困难的问题，到目前为止仍没有得到很好的解决。本文利用XL-800WF型光纤传输多功能脉冲激光加工系统对厚钢板进行多次脉冲照射，钢板熔化后在扩散过程中凝固，形成凝固图。由白光干涉仪测量了熔斑的直径，通过参考相关文献及液态金属的流速推算金属的凝固时间。根据液态钢的凝固时间，建立了理想条件下的热传导方程，求解热传导方程来计算激光的温度，从而模拟了激光瞬态温度场分布。结果表明，激光中心的温度约为2560 K，与以前的实验结果相比较，本文的结果与其吻合得较好。