Random vibration response analysis of Shenguang laser facility component based on PANDA platform
-
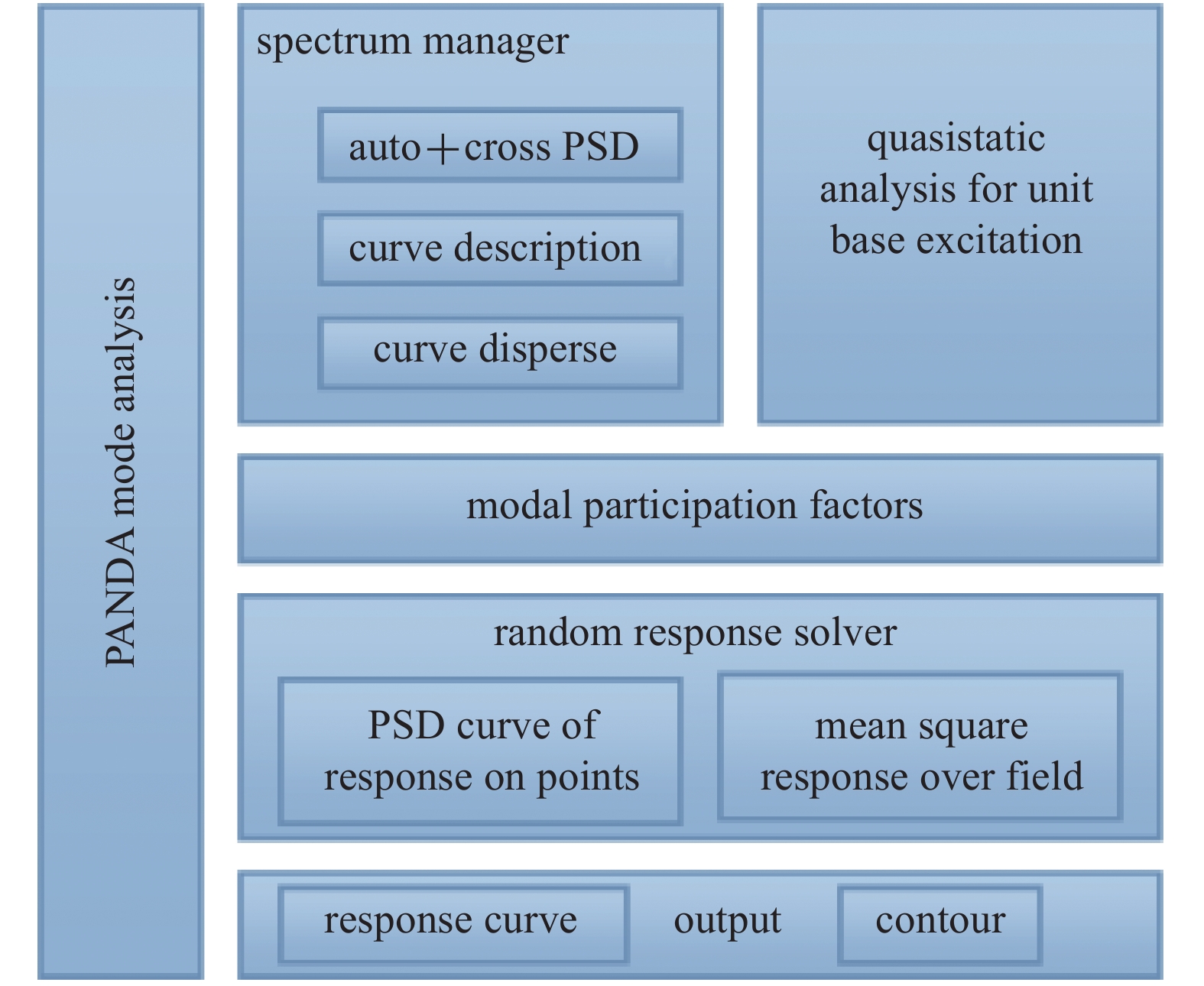
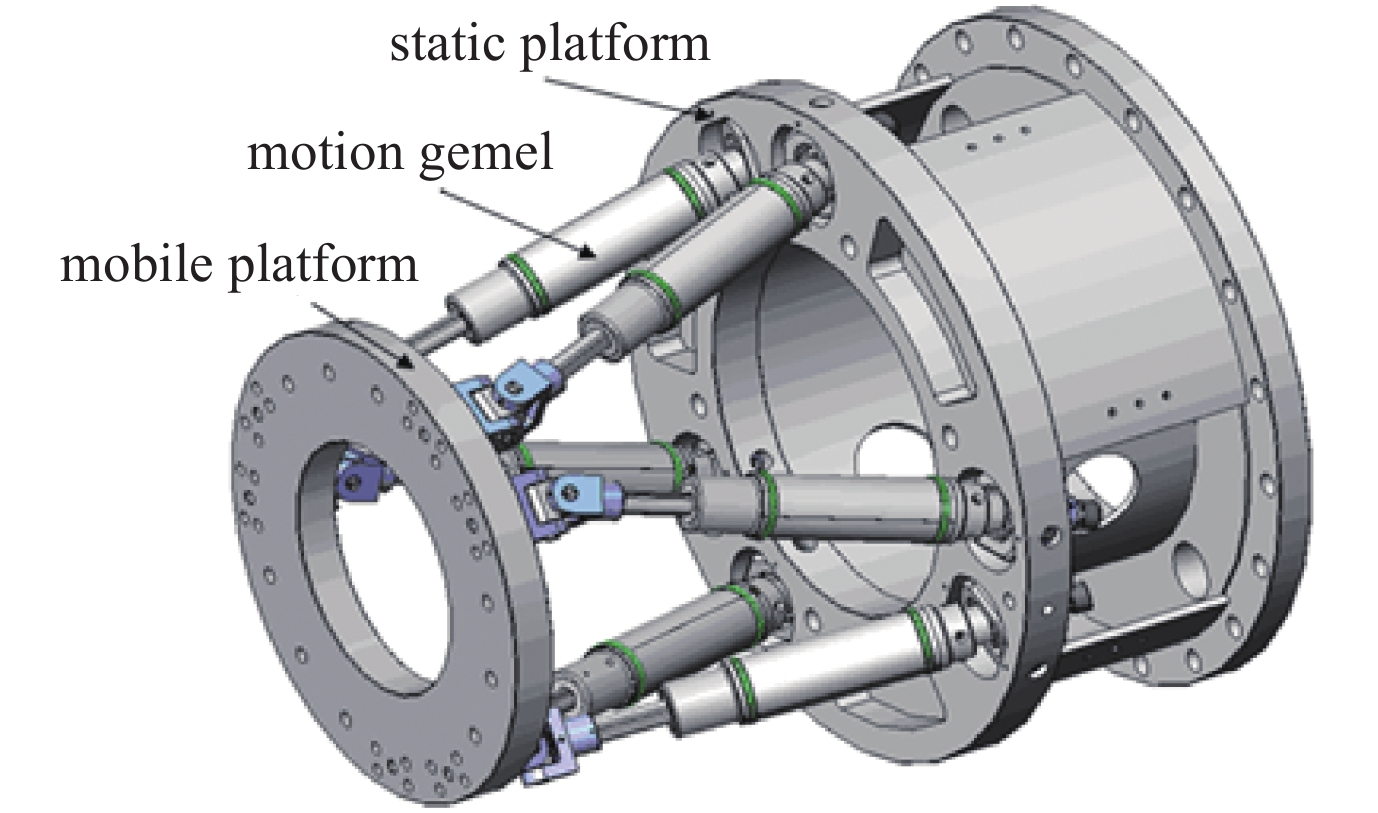
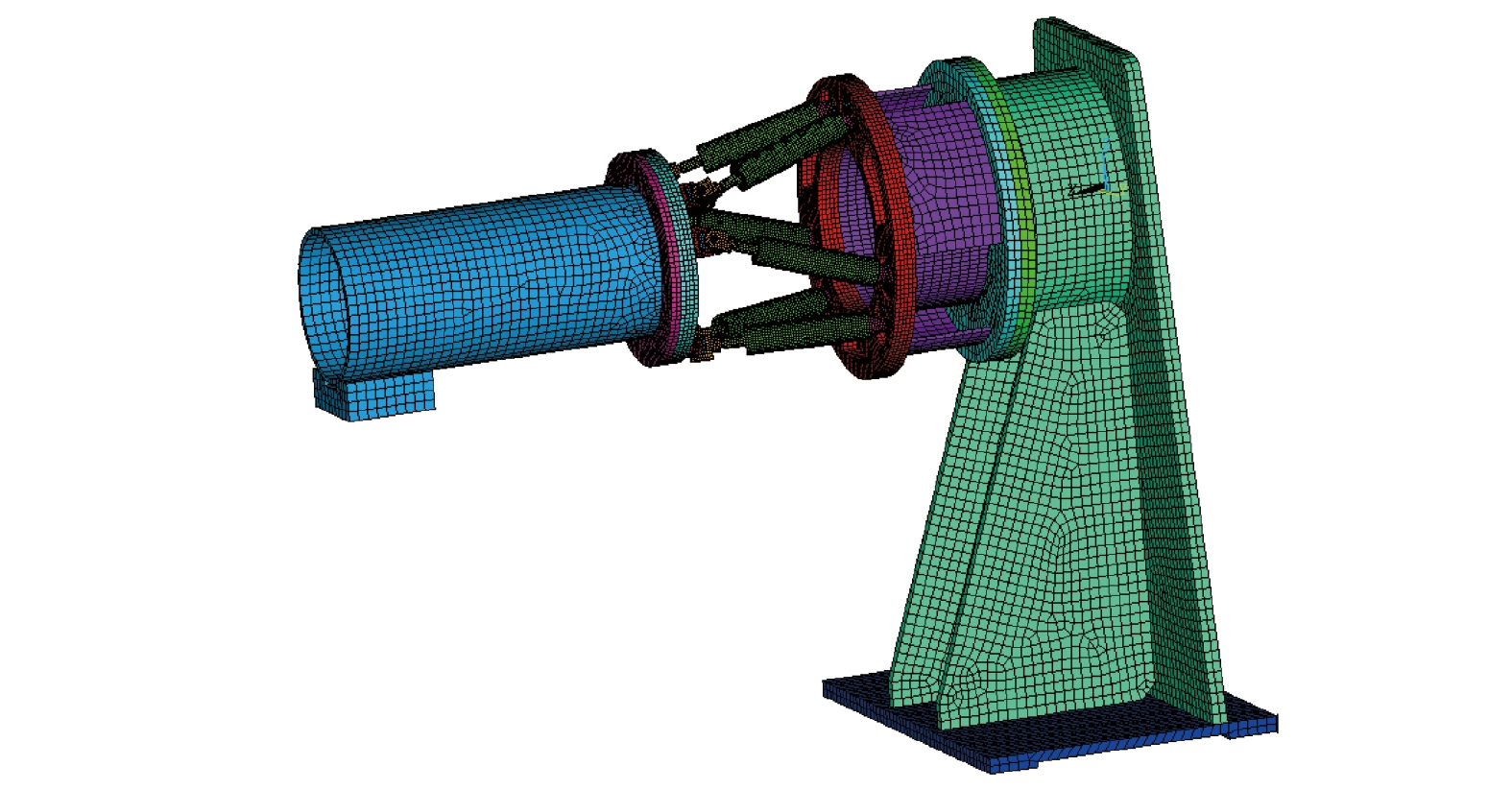
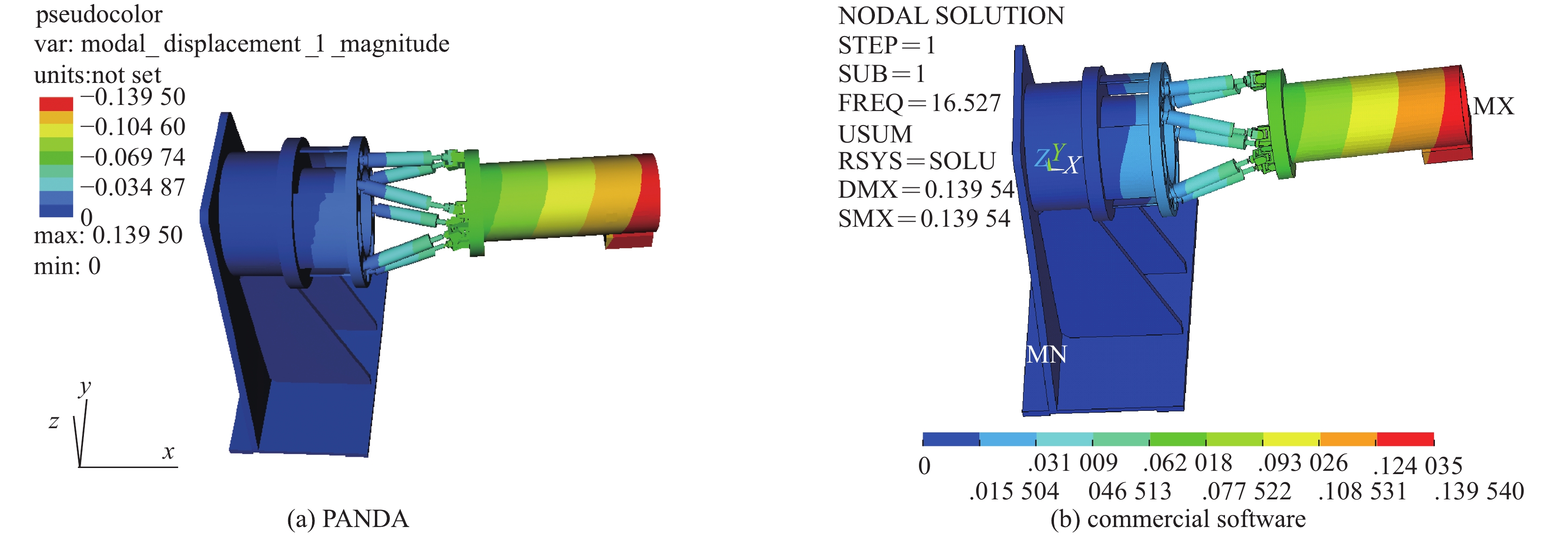
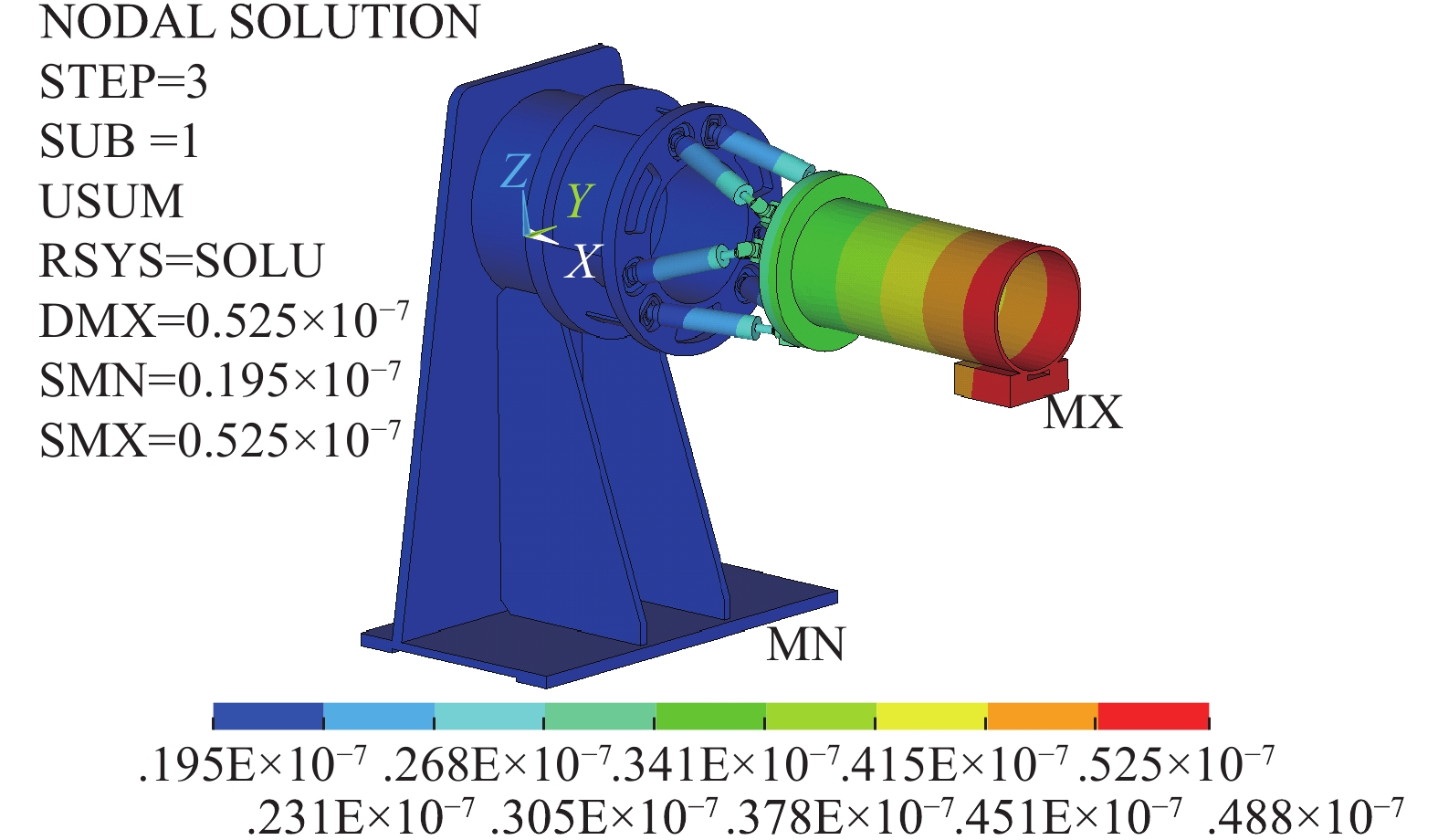
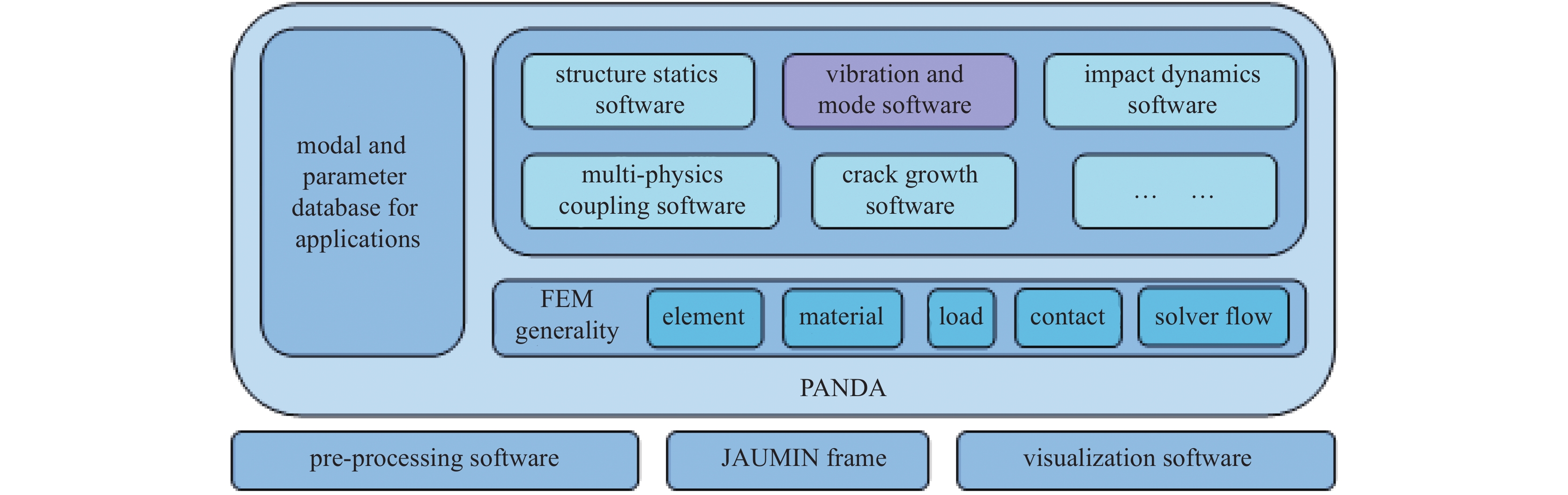
摘要: 基于PANDA自主并行计算平台,采用模态叠加法开展了多点基础激励作用下的随机振动响应分析算法设计和并行实现研究,构建了相应的并行求解模块。针对光机装置打靶样机中的六自由度平台结构,基于自主研发的软件模块,分析了该结构的模态特性及结构在地脉动载荷下的微振动响应,并与试验结果及商业软件分析结果进行了比对,在模态频率、振型和位移响应方面,都具有较好的一致性,验证了相关软件模块的正确性和PANDA平台在实际工程结构分析中的可用性。Abstract: Reliability design requirements for large and complex equipment pose new challenges to numerical simulation of structural dynamics. In this paper, based on self-developed parallel computing platform PANDA, the modal superposition method is used to calculate the random vibration response under multi-point foundation excitation. The algorithm design and parallel implementation are carried out, and the corresponding solving module is constructed. Taking the six-degree-of-freedom platform structure in the target positioning prototype of Shenguang facility as a numerical example, the modal and random vibration responses of the structure under ground fluctuating load are analyzed with our self-developed progress modules in PANDA platform. The analysis results are compared with the test results and commercial software analysis results. In terms of mode frequency, mode shape and displacement response, the results are consistent, which verifies the correctness of the relevant software and proves the feasibility of PANDA platform in actual engineering structural analysis. The correlative studies have important significance on solving dynamic analysis problems of complex equipments with autonomic software and breaking limitations of commercial finite element software.
-
表 1 结构前七阶固有频率比较
Table 1. The comparison of first five natural frequencies between simulation and test
rank experimentation
frequency/HzPANDA commercial software error between PAND and
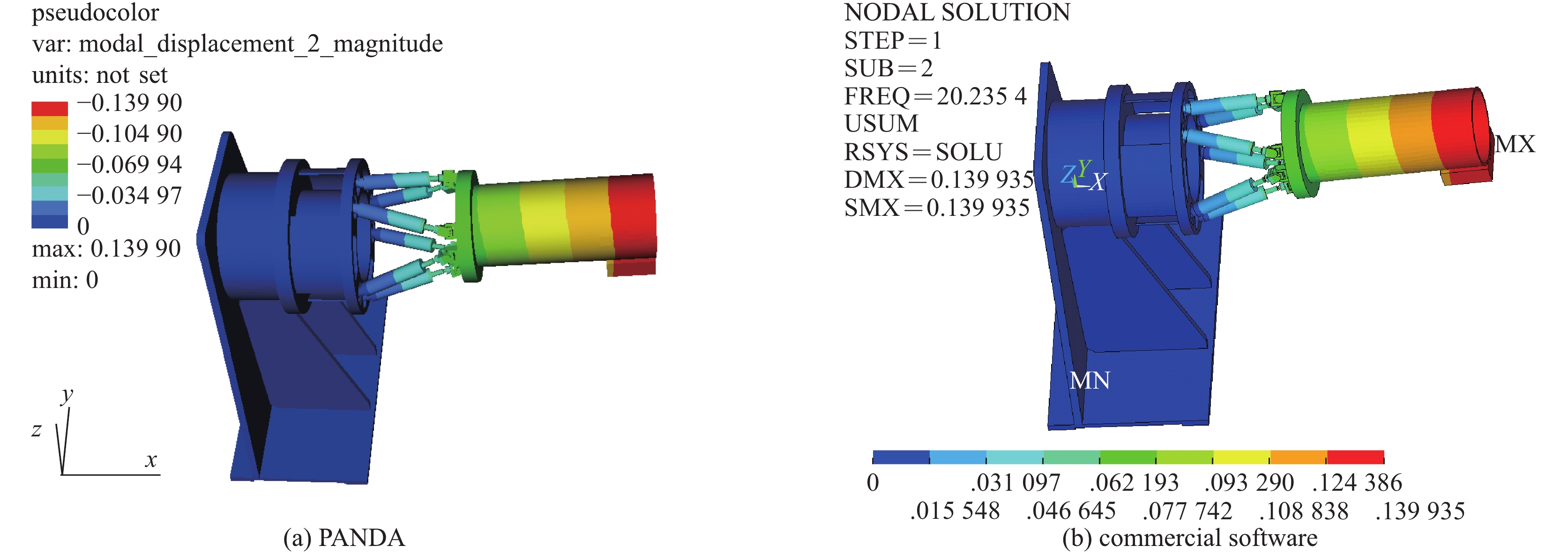
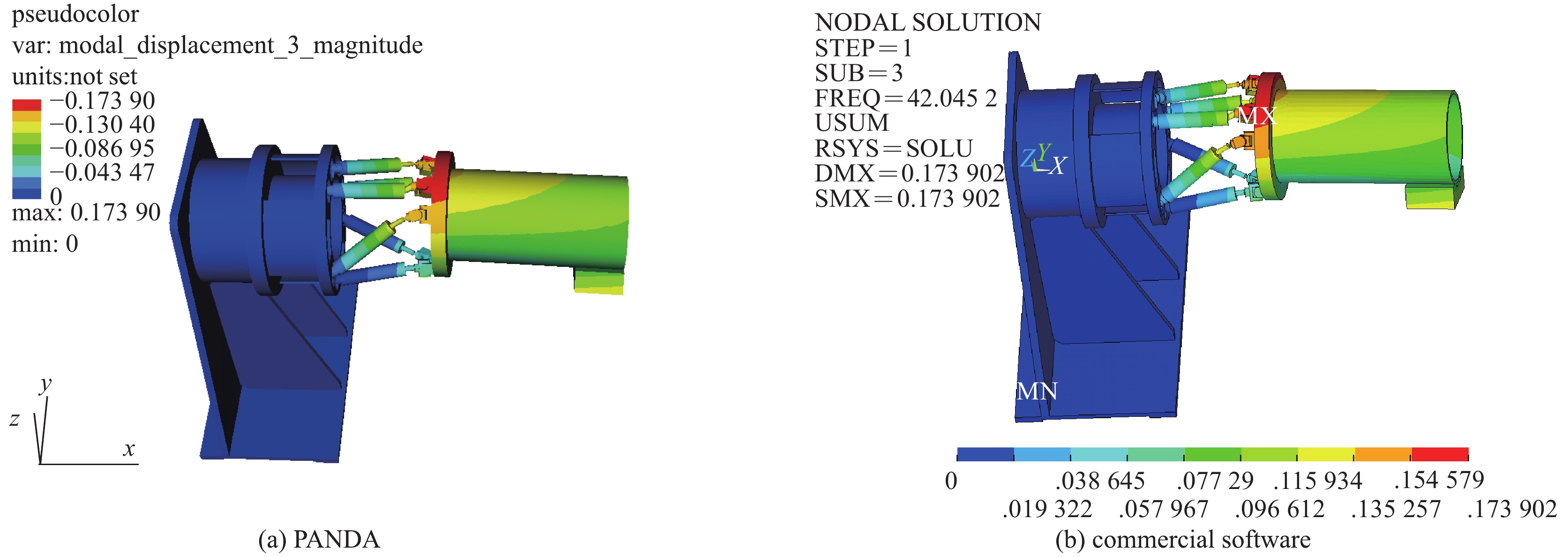
commercial software/%frequency/Hz error/% frequency/Hz error/% 1 16.52 16.49 −0.18 16.53 0.06 −0.24 2 20.26 20.21 −0.25 20.24 −0.10 −0.15 3 44.20 41.97 −5.05 42.05 −4.86 −0.19 4 53.66 54.42 1.42 54.47 1.51 −0.09 5 57.45 57.55 0.17 57.59 0.24 −0.16 6 − 71.17 − 71.46 − −0.41 7 − 88.01 − 88.48 − −0.53 表 2 结构测点合位移计算结果与试验结果比较
Table 2. The comparison of deform response between simulation and test
point experimentation PANDA commercial software error between PANDA and
commercial software/%deform response
range/10−2 μmmean value/
10−2 μmdeform response/
10−2 μmerror/% deform response/
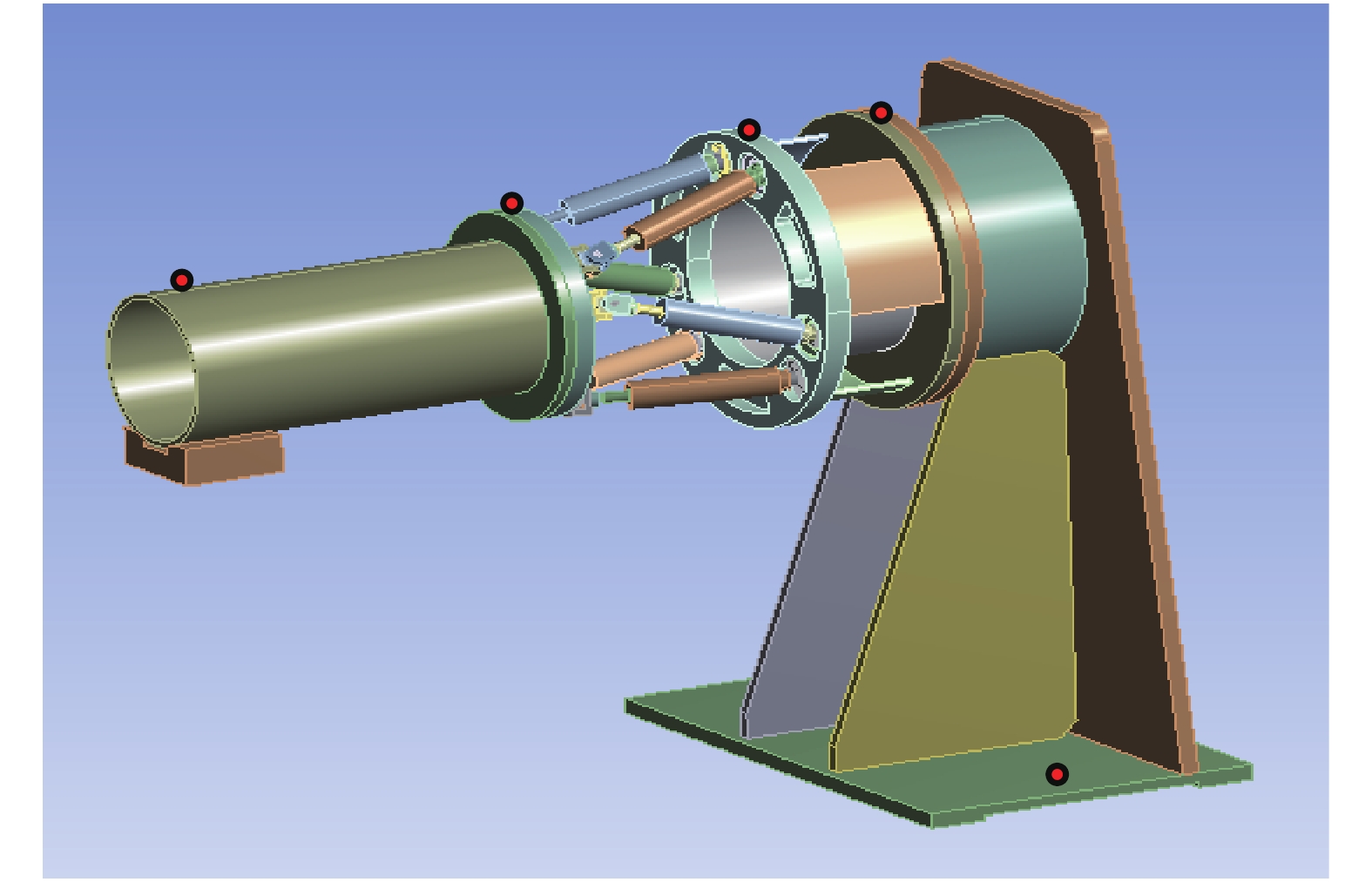
10−2 μmerror/% 1 [2.07, 2.47] 2.25 2.35 4.44 2.34 4.00 0.43 2 [2.03, 2.61] 2.30 2.56 11.30 2.58 12.17 −0.78 3 [2.16, 2.75] 2.44 2.66 9.02 2.69 10.16 −1.11 4 [2.99, 4.32] 3.73 4.03 8.04 4.07 9.06 −0.98 5 [4.66, 6.96] 5.99 6.01 0.33 6.02 0.57 −0.17 -
[1] 任健, 武林平, 申卫东. 基于JASMIN框架多物理耦合程序的性能优化及分析[J]. 计算物理, 2015, 32(4):431-436. (Ren Jian, Wu Linping, Shen Weidong. Performance optimization and analysis of multi-physics composition program on JASMIN[J]. Chinese Journal of Computational Physics, 2015, 32(4): 431-436 doi: 10.3969/j.issn.1001-246X.2015.04.008 [2] 张锐, 文立华, 校金友. 大规模声学边界元法的GPU并行计算[J]. 计算物理, 2015, 32(3):299-309. (Zhang Rui, Wen Lihua, Xiao Jinyou. GPU-accelerated boundary element method for large-scale problems in acoustics[J]. Chinese Journal of Computational Physics, 2015, 32(3): 299-309 doi: 10.3969/j.issn.1001-246X.2015.03.005 [3] Edwards C, Stewart J R. SIERRA: A software environment for developing complex multi-physics applications[C]//Proceedings of the 1st MIT Conference on Computational Fluid and Solid Mechanics. 2001. [4] Reese G M, Walsh T F, Bhardwaj M K. Salinas-theory manual[R]. SAND2011-8272, 2011. [5] 范宣华. 基于PANDA框架的大规模有限元模态分析并行计算及应用[D]. 北京: 北京大学, 2013.Fan Xuanhua. Parallel computation and applications of large-scale finite element modal analysis based on PANDA framework. Beijing: Peking University, 2013 [6] 成杰, 张林波. 三维结构分析并行自适应有限元软件PHG-Solid[J]. 计算机科学, 2012, 39(5):278-281. (Cheng Jie, Zhang Linbo. PHG-Solid: A parallel adaptive FEM software for 3D structural analysis[J]. Computer Science, 2012, 39(5): 278-281 doi: 10.3969/j.issn.1002-137X.2012.05.066 [7] 梁国平. 有限元语言[M]. 北京: 科学出版社, 2009.Liang Guoping. Finite element programming. Beijing: Science Press, 2009 [8] Liu Qingkai, Zhao Weibo, Cheng Jie, et al. A programming framework for large scale numerical simulations on unstructured mesh[C]//IEEE 2nd International Conference on High Performance and Smart Computing. 2016: 310-315. [9] Moses E I. Introduction to the National Ignition Facility [R]. UCRL-CONF-154962, 2004. [10] 范宣华, 陈璞, 吴瑞安, 等. 基于Jacobi-Davidson算法的大规模模态分析并行计算研究[J]. 振动与冲击, 2014, 33(1):203-208. (Fan Xuanhua, Chen Pu, Wu Ruian, et al. Parallel computing of large-scale modal analysis based on Jacobi-Davidson algorithm[J]. Journal of Vibration and Shock, 2014, 33(1): 203-208 doi: 10.3969/j.issn.1000-3835.2014.01.035 [11] 范宣华, 于晨阳, 王柯颖, 等. 大规模单点基础激励随机振动分析及并行计算[J]. 重庆理工大学学报(自然科学), 2017, 31(10):56-61. (Fan Xuanhua, Yu Chenyang, Wan Keying, et al. Parallel computation of large-scale random vibration analysis under single-point motion-based excitation[J]. Journal of Chongqing University of Technology: Natural Science, 2017, 31(10): 56-61 [12] 范宣华, 肖世富, 陈璞, 等. 大规模结构动力学并行计算与软件研发进展[J]. 力学季刊, 2016, 3(1):421-432. (Fan Xuanhua, Xiao Shifu, Chen Pu, et al. Advances in the parallel computation and software development of large-scale structural dynamics[J]. Chinese Quarterly of Mechanics, 2016, 3(1): 421-432 -




 下载:
下载: