Research on terahertz radiation peak control of photoconductive antenna
-
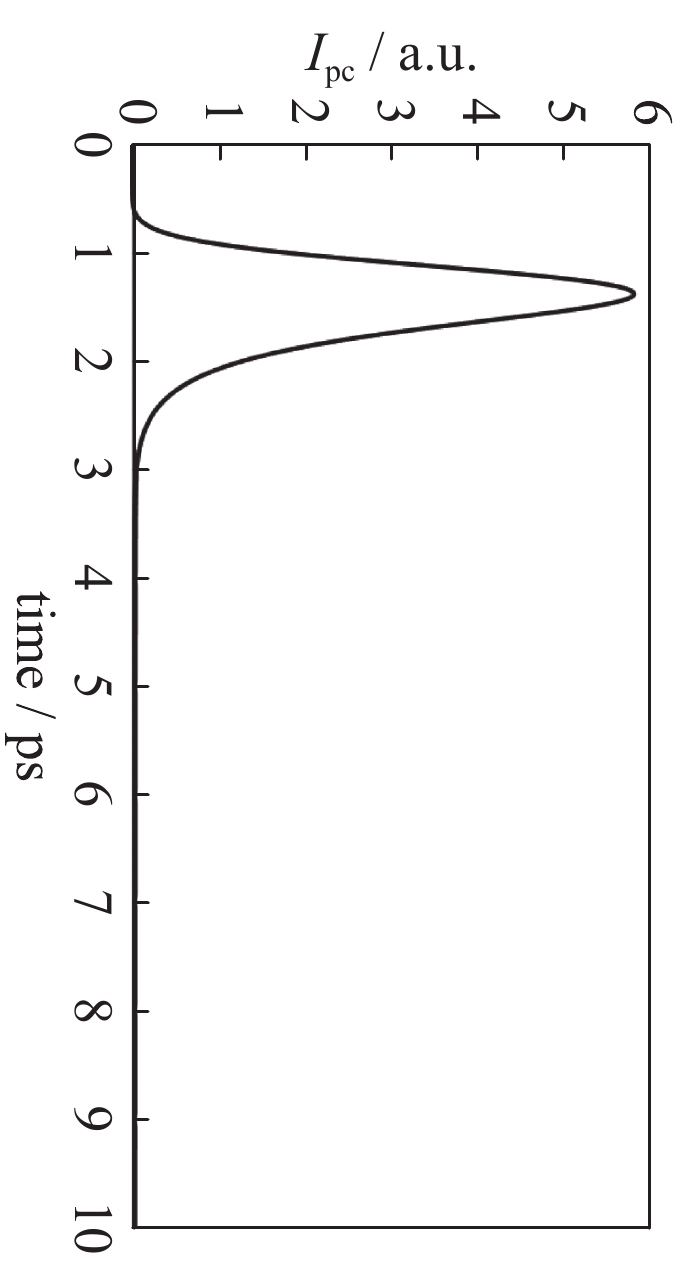
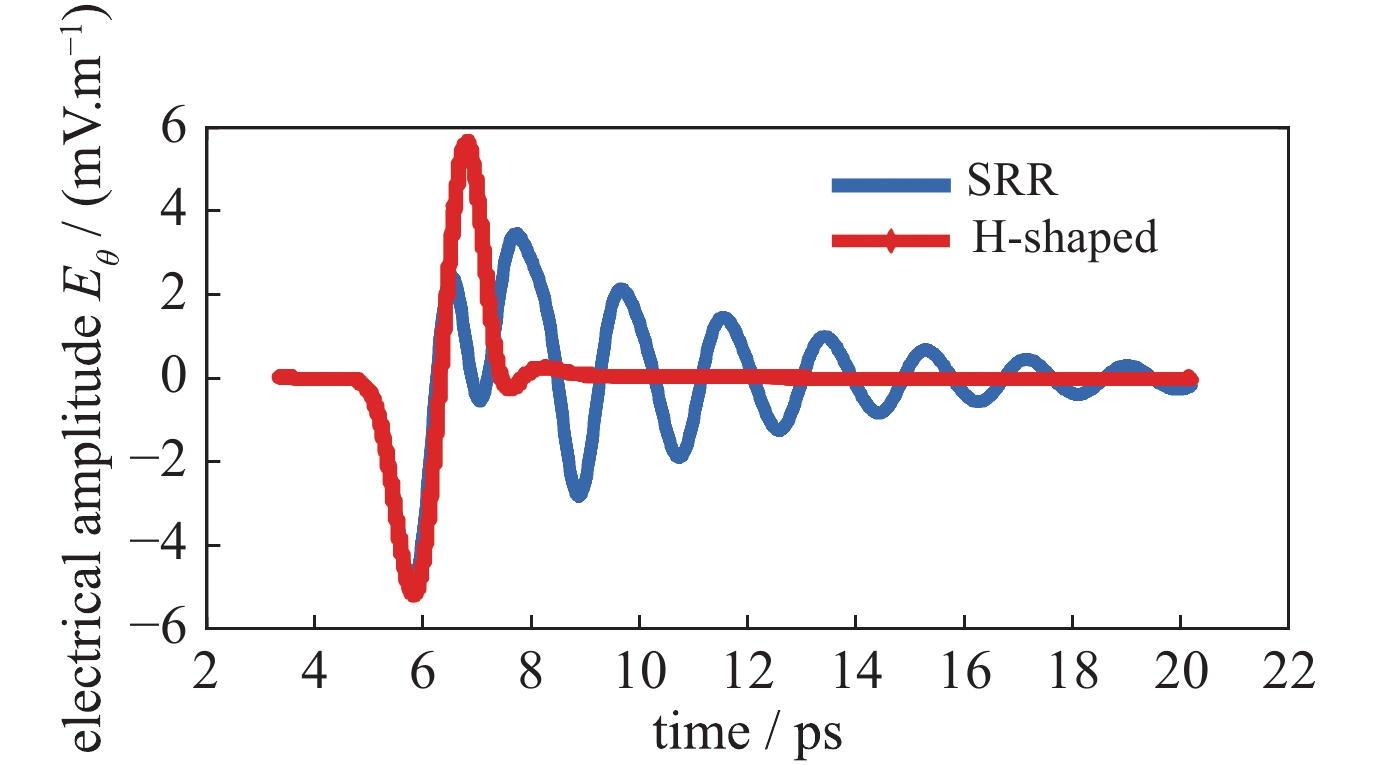
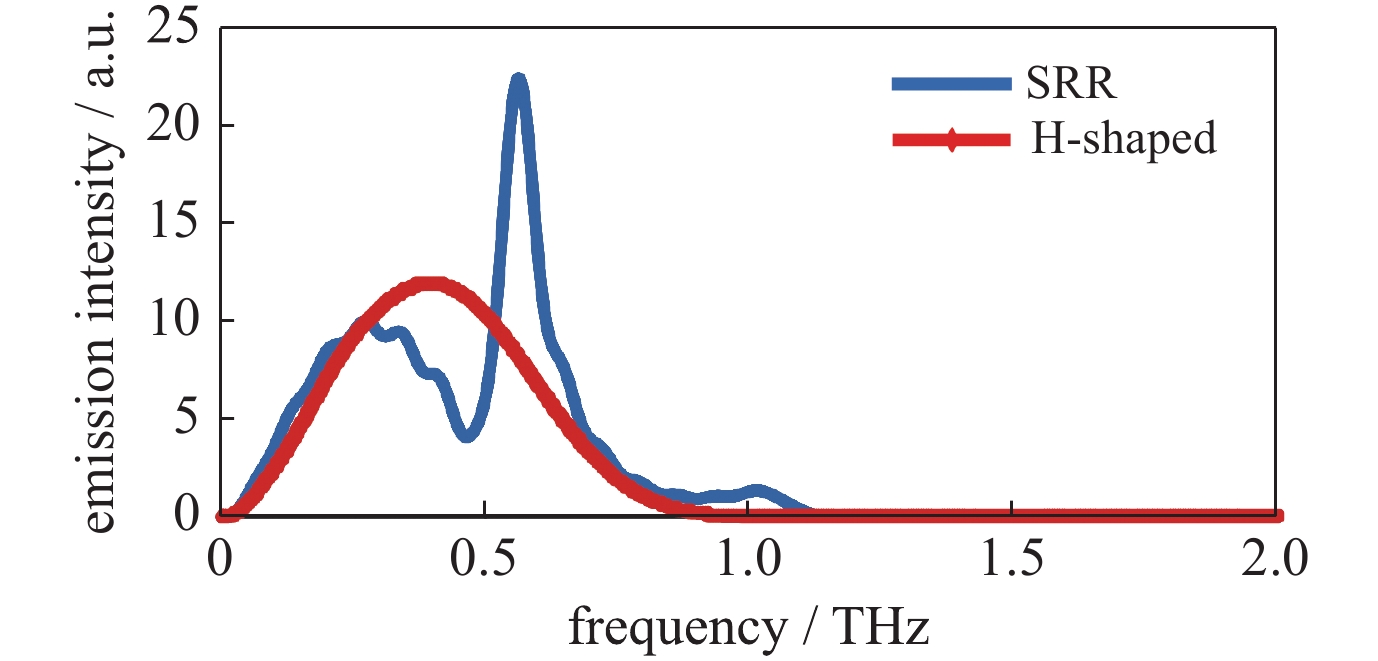
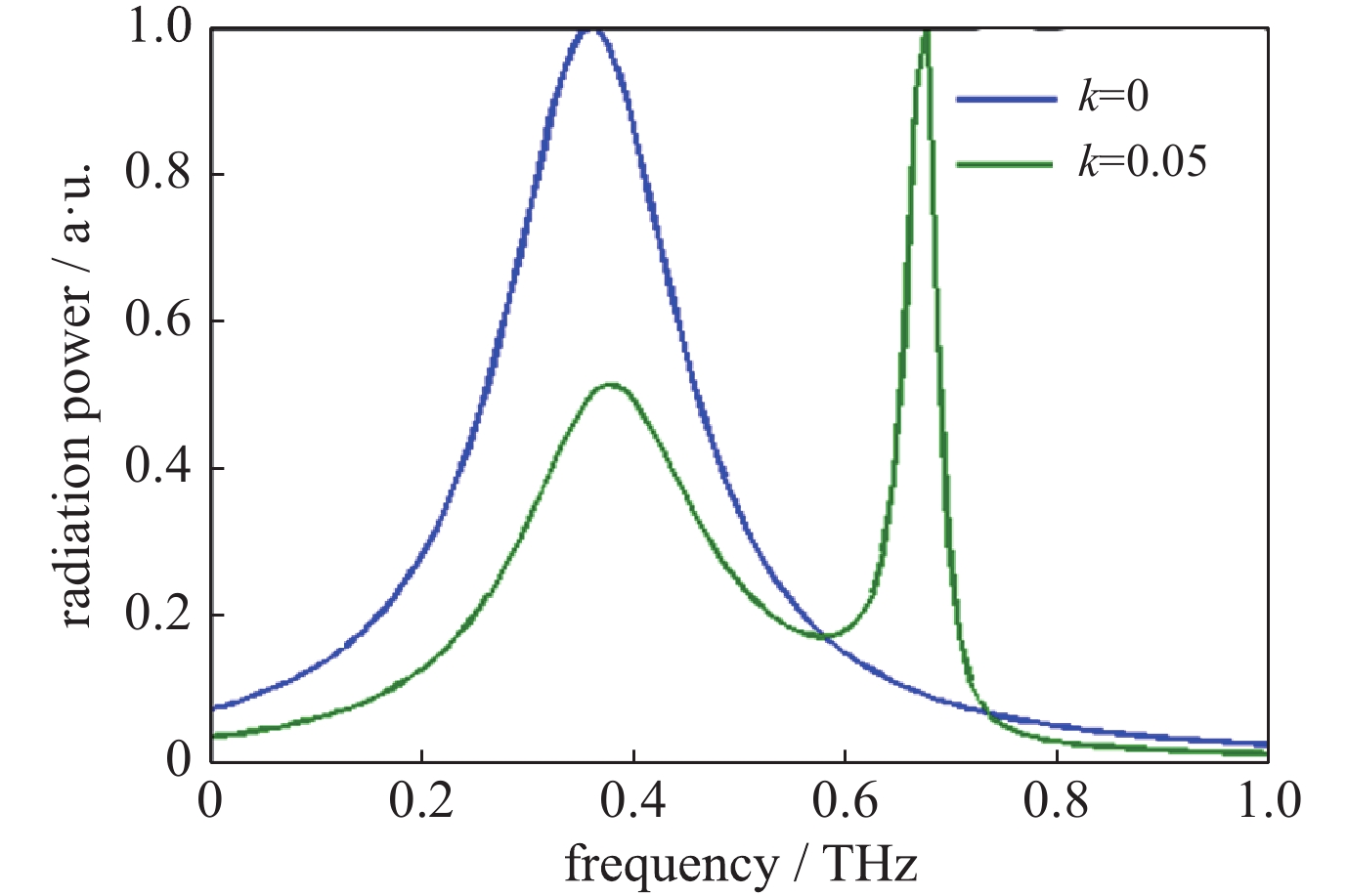
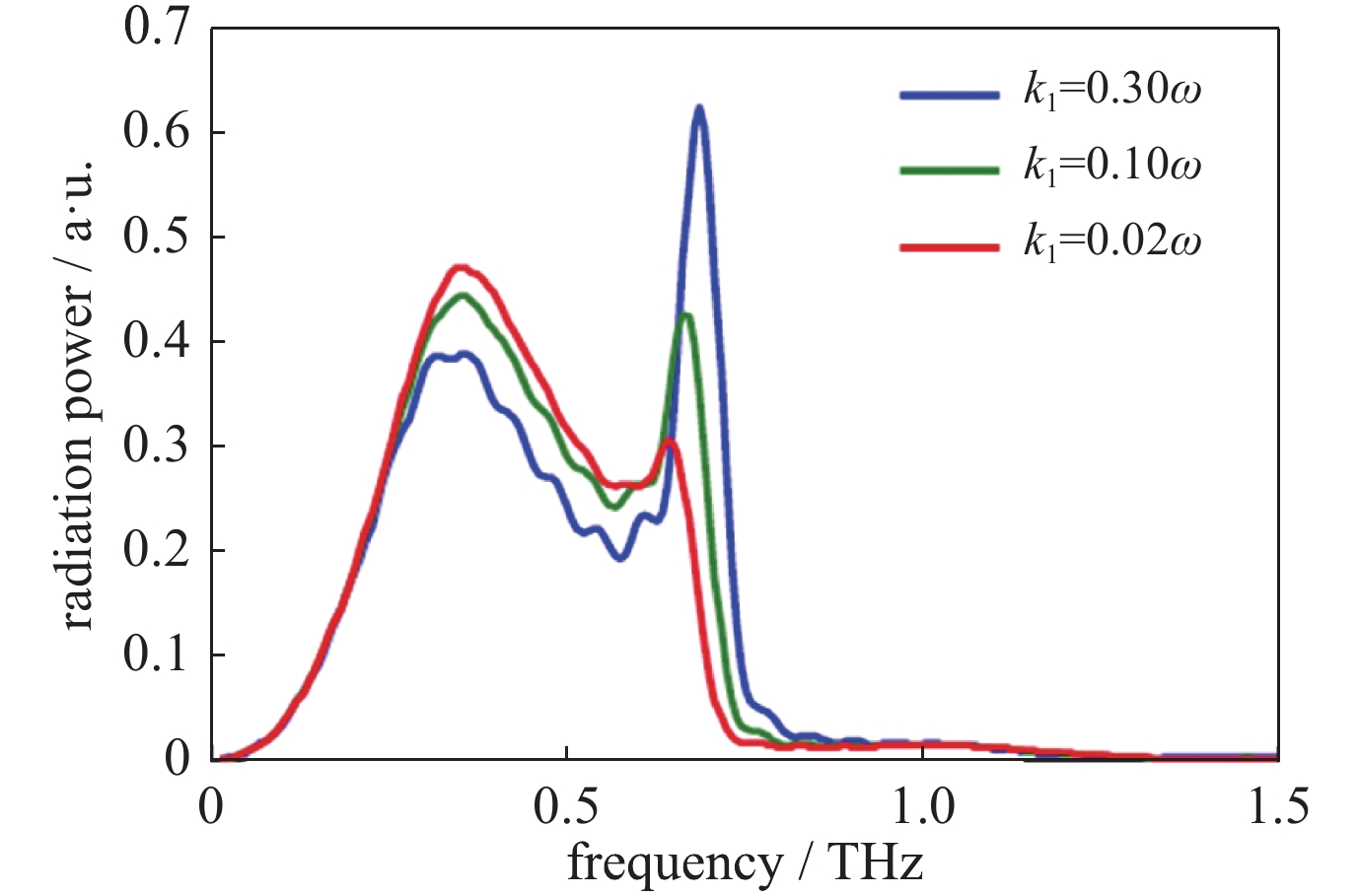
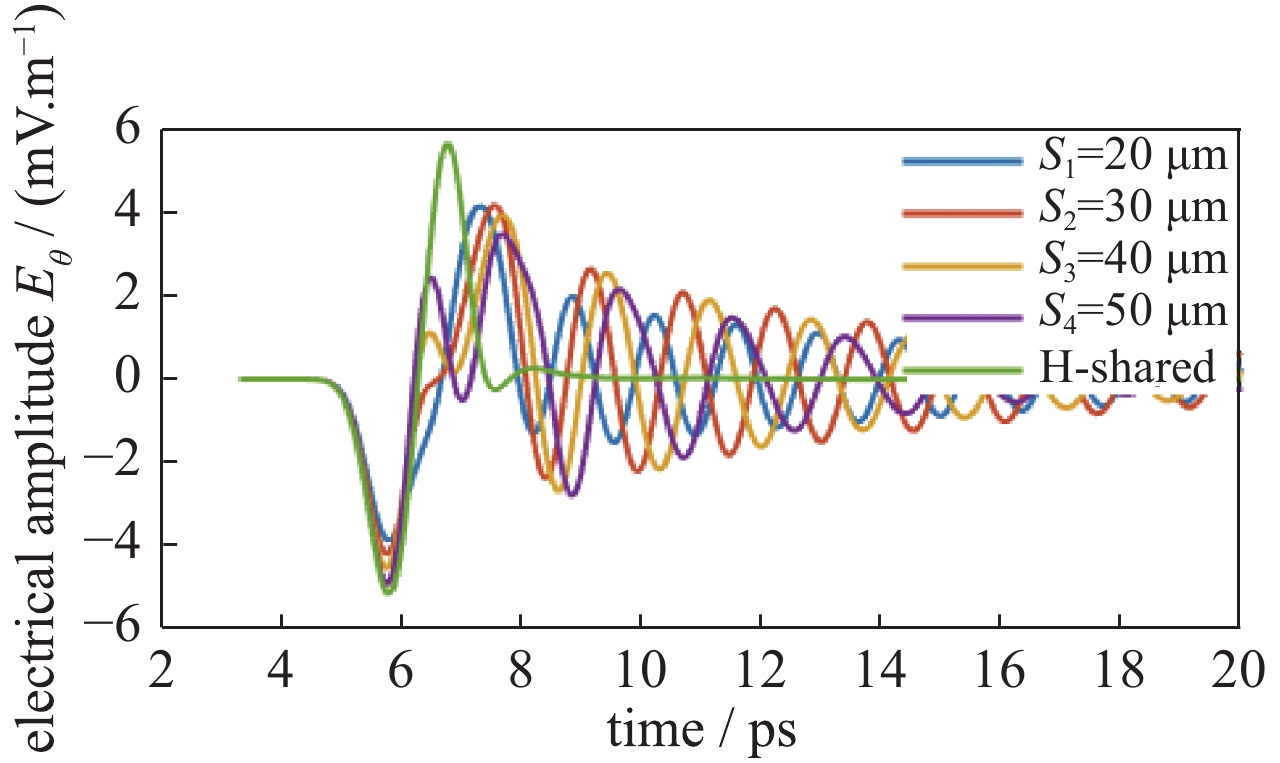
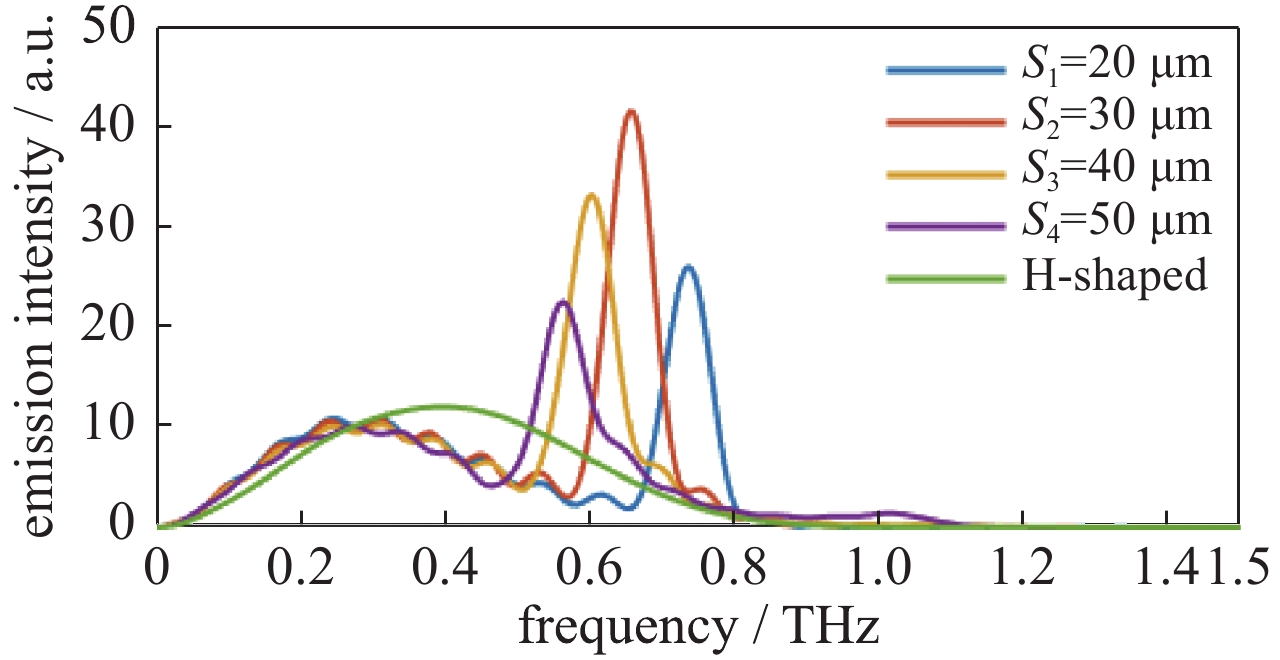
摘要: 针对微结构光电导天线与飞秒激光之间相互作用效应以及辐射太赫兹波调控问题进行了研究。采用德鲁德-洛伦兹理论模型获得微结构光电导天线辐射光电流密度,通过时域有限差分把光电流密度迭代在激励网格上,结合麦克斯韦方程求解时变电磁场,并通过传输线格林函数获得多层介质近场到远场的辐射太赫兹波,建立了辐射光电流与辐射阻抗、电磁共振模式之间的关系模型,模拟仿真分析了微结构S型光电导天线太赫兹波辐射调控机理。研究结果表明:微结构改变了天线等效模型的辐射阻抗;同时得知耦合系数不为零时存在耦合作用,且随着耦合系数增大共振频率峰值发生辐射增强和位移;并通过设计S型光电导天线获得辐射峰值频率调整范围为0.50~0.80 THz之间,对比工形天线辐射峰值频率由原来的0.40 T移动到0.76 T,频率调整度75%,峰值辐射效率约提高70%。该研究工作为后续高功率光导天线太赫兹波辐射的共振中心频点以及结构设计奠定重要基础。Abstract: This paper studies the interaction effect between the micro-structure photoconductive antenna (PCA) and femtosecond laser, the control of radiated terahertz (THz) wave, and the radiation regulation mechanism of the THz wave for the photoconductive antenna (PCA). The Drude-Lorentz theory model is used to solve the photocurrent density, which is then iterated to the excitation grid by FDTD method. And then the time-varying electromagnetic fields is solved by Maxwell’s equations. The radiated THz wave from the near field to far field in the multi-layer medium is got through the Green's Function of transmission line, and the relationship between the photocurrent and impedance of the radiation is established. At the same time, the relationship between the photocurrent and the magnetic resonance model is also established. The control mechanism of THz wave radiation from micro-structure S-shaped PCA is analyzed by simulation. The results show that the radiation impedance of the equivalent model is changed after split ring resonator (SRR) is introduced into the H-shaped PCA. Meanwhile, it is known that the coupling effect exists when the coupling coefficient is not zero. With the increasing of the coupling coefficient, and the radiation intensity of the resonance frequency peak increases and shifts. The adjusting range of the center frequency between 0.50−0.80 THz, the frequency modulation degree is 75%, and the peak radiation efficiency increases by 70% after simulating the S-shaped PCA. This work lays an important foundation for the design of THz wave resonance center frequency range and structure of high-power PCA.
-
表 1 数值仿真模拟实验物理与工作参数
Table 1. Physical and working parameters of the numerical simulation experiment
parameter symbol value unit absolute temperature $T$ 300 K laser wavelength $\lambda $ 800 nm optical absorption coefficient $\alpha $ 10 000 cm−1 carrier relaxation time ${\tau _{\rm{s}}}$ 30 fs delay time of Gaussian pulse ${t_0}$ 4 ps carrier lifetime ${\tau _{\rm{c}}}$ 0.1 ps electron mobility $\;{\mu _{\rm{n}}}$ 200 cm2·V−1·s−1 carrier recombination time ${\tau _{{\rm{rec}}}}$ 10 ps semiconductor dielectric constant $\varepsilon $ 13.18 − bias voltage ${V_{\rm{b}}}$ 60 V repetition frequency ${f_{{\rm{rep}}}}$ 80 MHz laser pulse width ${\tau _{\rm{p}}}$ 120 fs geometric factor $\xi $ 3 − thickness of the substrate ${T_{\rm{h}}}$ 20 µm 表 2 光电导天线结构与结构计算区域参数
Table 2. Structure parameters for PCA and structure calculation area
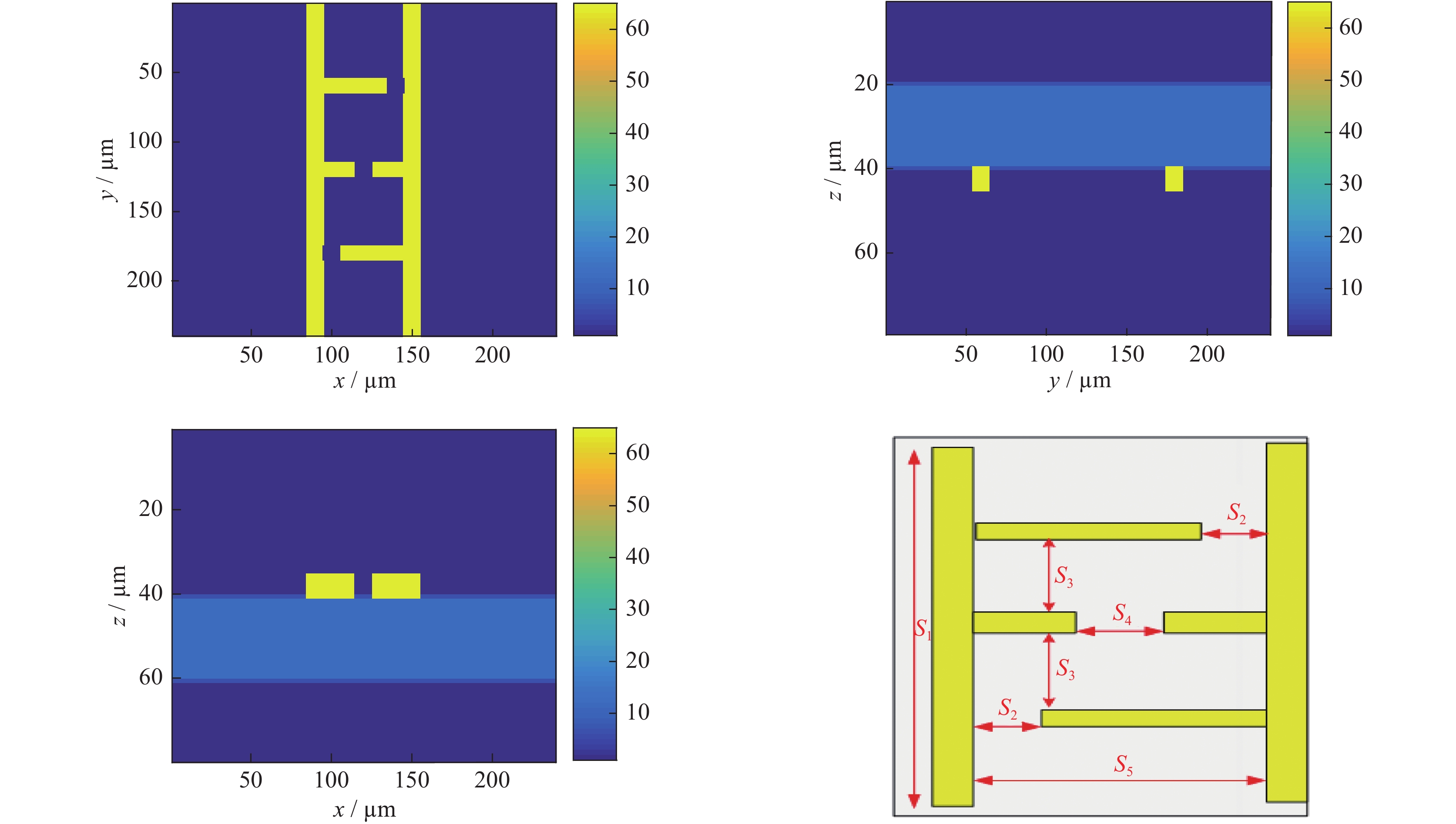
parameter symbol value unit length of structure calculation area ${L_x}$ 240 µm width of structure calculation area ${L_y}$ 240 µm thickness of structure calculation area ${L_z}$ 80 µm width of antenna metal $W$ 10 µm ground thickness ${h_{\rm{m}}}$ 5 µm length of biased lines of s-shaped antenna ${S_1}$ 250 µm separation of biased lines and microstructure of s-shaped antenna ${S_2}$ 10 µm distance between microstructure and antenna electrode ${S_3}$ 20,30,40 µm photoconductive gap ${S_4}$ 10 µm separation between the lines ${S_5}$ 50 µm -
[1] Zhang J, Tuo M, Liang M, et al. Contribution assessment of antenna structure and in-gap photocurrent in terahertz radiation of photoconductive antenna[J]. Journal of Applied Physics, 2018, 124: 053107. doi: 10.1063/1.5038341 [2] Nissiyah G J, Madhan M G. Graphene-based photoconductive antenna structures for directional terahertz emission[J]. Plasmonics, 2019, 14(4): 891-900. doi: 10.1007/s11468-018-0871-7 [3] Bowman T, El-Shenawee M. Nondestructive imaging of packaged microelectronics using pulsed terahertz technology[J]. Int Symp Microelectron, 2017(1): 709-714. [4] Cheon H, Yang H, Lee S, et al. Terahertz molecular resonance of cancer DNA[J]. Scientific Reports, 2016, 6(1): 37103. doi: 10.1038/srep37103 [5] Davies A G, Burnett A D, Fan W, et al. Terahertz spectroscopy of explosives and drugs[J]. Materials Today, 2008, 11(3): 18-26. doi: 10.1016/S1369-7021(08)70016-6 [6] Gowen A A, O’Sullivan C, O’Donnell C P. Terahertz time domain spectroscopy and imaging: Emerging techniques for food process monitoring and quality control[J]. Trends in Food Science & Technology, 2012, 25(1): 40-46. [7] O’Hara J F, Chen H T, Taylor A J, et al. Split-ring resonator enhanced terahertz antenna[J]. Nonlinear Optics: Materials, Fundamentals and Applications, 2007, TuB2. [8] Takano K, Chiyoda Y, Nishida T, et al. Optical switching of terahertz radiation from meta-atom-loaded photoconductive antennas[J]. Applied Physics Letters, 2011, 99: 161114. doi: 10.1063/1.3654156 [9] Miyamaru F, Saito Y, Takeda M W, et al. Emission of terahertz radiations from fractal antennas[J]. Applied Physics Letters, 2009, 95: 221111. doi: 10.1063/1.3271181 [10] Zhisheng Piao M T A K. Carrier dynamics and terahertz radiation in photoconductive antennas[J]. Japanese Journal of Applied Physics, 2000, 39(96): 96-100. [11] Lee Y S. Principles of terahertz science and technology[M]. New York: Springer Science & Business Media, 2009. [12] Ma C, Yang L, Dong C, et al. An experimental study on LT-GaAs photoconductive antenna breakdown mechanism[J]. IEEE Trans Electron Devices, 2018, 65(3): 1043-1047. doi: 10.1109/TED.2018.2790920 [13] Moreno E, Sohrabi R, Klochok G, et al. Vertical versus planar pulsed photoconductive antennas that emit in the terahertz regime[J]. Optik, 2018, 166: 257-269. doi: 10.1016/j.ijleo.2018.03.096 [14] Malhotra I, Thakur P, Pandit S, et al. Analytical framework of small-gap photoconductive dipole antenna using equivalent circuit model[J]. Optical and Quantum Electronics, 2017, 49(10). [15] Prajapati J, Bharadwaj M, Chatterjee A, et al. Circuit modeling and performance analysis of photoconductive antenna[J]. Optics Communications, 2017, 394: 69-79. doi: 10.1016/j.optcom.2017.03.004 [16] Castañeda-Uribe O A, Criollo C A, Winnerl S, et al. Comparative study of equivalent circuit models for photoconductive antennas[J]. Optics Express, 2018, 26(22): 29017. doi: 10.1364/OE.26.029017 [17] Liang H, Shi S, Ma L. Coupled-mode theory of nonparallel optical waveguides[J]. Journal of Lightwave Technology, 2007, 25(8): 2233-2235. doi: 10.1109/JLT.2007.899783 [18] Torkaman P, Darbari S, Mohammad-Zamani M J. Design and simulation of a piezotronic GaN-based pulsed THz emitter[J]. Journal of Lightwave Technology, 2018, 36(17): 3645-3651. doi: 10.1109/JLT.2018.2844219 [19] Khorshidi M, Dadashzadeh G. Dielectric structure with periodic strips for increasing radiation power of photoconductive antennas: Theoretical analysis[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2017, 38(5): 609-629. doi: 10.1007/s10762-016-0354-x -




 下载:
下载: