基于JASMIN的并行CP-FDTD建模与屏蔽效能评估应用

李俊辛; 刘强; 闫丽萍; 赵翔; 孟雪松; 周海京

doi:10.11884/HPLPB201931.190026

基于JASMIN的并行CP-FDTD建模与屏蔽效能评估应用

doi: 10.11884/HPLPB201931.190026

1.
四川大学电子信息学院, 成都 610065
2.
北京应用物理与计算数学研究所, 北京 100088

基金项目:

国家自然科学基金项目 61877041

详细信息

作者简介:
李俊辛(1992—)，男，硕士，主要从事电磁场数值计算方面的研究；andy_ruohan@outlook.com

通讯作者:
闫丽萍(1972—)，女，教授，主要从事电磁兼容建模分析与电磁效应评估方面的研究；liping_yan@scu.edu.cn

中图分类号: O441.4
计量
- 文章访问数: 1179
- HTML全文浏览量: 255
- PDF下载量: 78
- 被引次数: 0
出版历程
- 收稿日期: 2019-01-30
- 修回日期: 2019-03-20
- 刊出日期: 2019-05-15

JASMIN-based parallel CP-FDTD modeling and application to shielding effectiveness prediction

1.
Department of Electronic and Information Engineering, Sichuan University, Chengdu 610065, China
2.
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

摘要

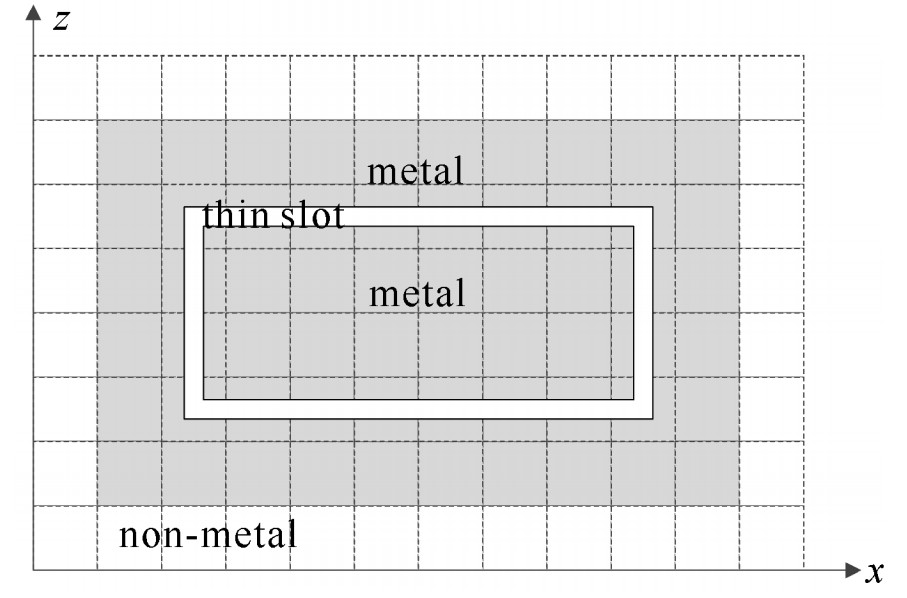
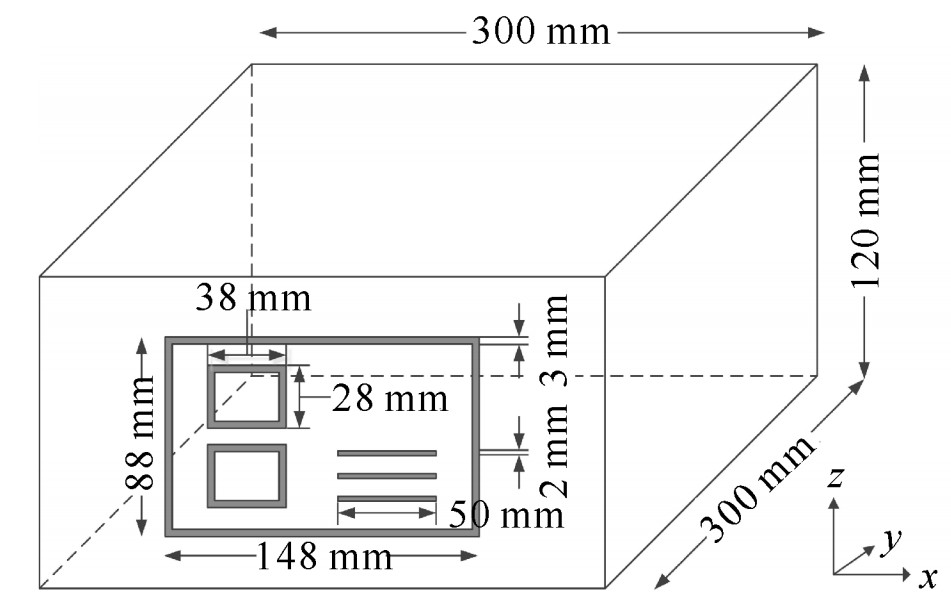
摘要: 时域有限差分(FDTD)中采用环路法(CP)进行复杂金属细缝结构建模，可突破细缝结构对空间步长的约束而大大减少计算资源的消耗。提出CP-FDTD在大规模并行化平台的建模方法，通过对工程金属细缝结构自动建模以及对CP算法的自动适配，实现CP-FDTD的并行化处理。利用所开发的并行CP-FDTD算法分析了开不同工程细缝金属腔在0.05~3.00 GHz内的电磁屏蔽效能，结果表明所开发的具有金属细缝建模功能的并行化CP-FDTD自动适配处理技术，与加密网格的传统FDTD(fine-FDTD)计算结果吻合良好，且计算效率显著提升。
- 并行化 /
- 细缝 /
- 环路法 /
- 时域有限差分法 /
- 屏蔽效能
Abstract: The contour path (CP) based modeling of thin slots in finite-difference time-domain (FDTD) simulation of complex structures breaks the constraint that the mesh size should be less than the smallest dimension of thin slots to get more accurate results, and therefore greatly reduce the consumption of computing resources. A large-scale parallelization platform JASMIN based modeling method of CP-FDTD is proposed in this paper. The thin slots can be automatically modeled and adaptively allocated in the proposed parallelized CP-FDTD algorithm. The electromagnetic shielding effectiveness (SE) of the metal cavity with different thin slots commonly used in industry is analyzed at the frequency range of 0.05 GHz to 3.00 GHz using the proposed parallel CP-FDTD algorithm. Results show that the SEs predicted using the developed parallel CP-FDTD are in good agreement with those obtained using finely meshed FDTD (fine-FDTD). Moreover, the computational efficiency is significantly improved.
- parallelization /
- thin slot /
- contour path /
- finite-difference time-domain /
- shielding effectiveness

HTML全文

图 1 Yee网格中的细缝及环路法示意图

Figure 1. Thin slot in the Yee's cell and the schematic diagram of contour path(CP) method

下载: 全尺寸图片幻灯片

图 2 位于金属面板上的环形缝模型

Figure 2. An annular seam on a metal plate

下载: 全尺寸图片幻灯片

图 3 含不同形状细缝的网格

Figure 3. Cells with thin slots in different shape

下载: 全尺寸图片幻灯片

图 4 type3类型网格在各个面上的积分路径

Figure 4. Contour path of thin slot in type3 cell on each plane

下载: 全尺寸图片幻灯片

图 5 CP算法在JASMIN并行化平台的数据架构

Figure 5. Data architecture of CP algorithm in JASMIN parallelization platform

下载: 全尺寸图片幻灯片

图 6 居于子patch计算空间中的环形缝模型

Figure 6. Annular seam in the sub-patch calculation space

下载: 全尺寸图片幻灯片

图 7 带有多种不同细缝结构的金属腔

Figure 7. Metal cavity with multiple thin slots

下载: 全尺寸图片幻灯片

图 8 不同极化方式下金属腔中心点SE计算结果的对比

Figure 8. SE prediction at the center of the enclosure for vertical and horizontal polarizations using CP-FDTD and fine-FDTD

下载: 全尺寸图片幻灯片

图 9 斜入射时的计算模型

Figure 9. Calculation model for oblique incidence

下载: 全尺寸图片幻灯片

图 10 平面波斜入射条件下金属腔中心点SE计算结果的对比

Figure 10. SE prediction at the center of the enclosure with oblique incident plane wave

下载: 全尺寸图片幻灯片

图 11 CP-FDTD并行程序加速比与运算核心数的关系

Figure 11. Speedup ratio of parallel CP-FDTD program with respect to the number of CPU cores

下载: 全尺寸图片幻灯片

表 1 不同极化方式下金属腔内主要谐振频点和相应模式

Table 1. Main resonant frequency points and modes of the metal enclosure with different polarization

vertical polarization	frequency/GHz	0.77	1.17	1.64	2.20	2.31	2.64	2.75
vertical polarization	resonant mode	TE₁₀₁	TE₁₀₂/TE₂₀₁	TE₁₀₃/TE₃₀₁	TE₃₀₃	TE₃₁₂/TM₃₁₂	TE₁₀₅/TE₅₀₁	TE₁₂₀/TM₁₂₀
horizontal	frequency/GHz	1.46	1.70	1.78	2.07	2.30	2.69	2.92
polarization	resonant mode	TE₀₁₁	TE₀₁₂	TE₂₁₁/TM₂₁₁	TE₀₁₃	TE₂₁₃/TM₂₁₃	TE₂₁₄/TM₂₁₄/TE₄₁₂/TM₄₁₂	TE₀₁₅

下载: 导出CSV

表 2 Fine-FDTD与CP-FDTD的计算成本对比

Table 2. Comparison of calculation cost between fine-FDTD and CP-FDTD

model	method	total cells	computation time/min
model in Fig. 7	fine-FDTD CP-FDTD	5.44×10⁶ 0.64×10⁶	836.50 77.94
model in Fig. 9	fine-FDTD CP-FDTD	4.35×10⁶ 0.64 ×10⁶	784.84 72.11

下载: 导出CSV

参考文献(14)

[1]	葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 3版. 西安: 西安电子科技大学出版社, 2011. Ge Debiao, Yan Yubo. Finite-difference time-domain method for electromagnetic waves. 3rd ed. Xi'an: Xidian University Press, 2011
[2]	Kuo C W, Kuo C M. Finite-difference time-domain analysis of the shielding effectiveness of metallic enclosures with apertures using a novel subgridding algorithm[J]. IEEE Trans Electromagnetic Compatibility, 2016: 1-7.
[3]	Bérenger J P. The Huygens subgridding for the numerical solution of the Maxwell equations[J]. Journal of Computational Physics, 2011, 230(14): 5635-5659. doi: 10.1016/j.jcp.2011.03.046
[4]	Huang Z. A synchronized multigrid time domain method via Huygens subgridding and implicit algorithms[J]. IEEE Trans Antennas & Propagation, 2013, 61(5): 2605-2614.
[5]	Wang Jianbao, Wang Jinlong, Zhou Bihua, et al. An efficient 3-D HIE-FDTD method with weaker stability condition[J]. IEEE Trans Antennas & Propagation, 2016, 64(3): 998-1004.
[6]	Movahhedi M, Abdipour A, Nentchev A, et al. Alternating-direction implicit formulation of the finite-element time-domain method[J]. IEEE Trans Microwave Theory and Techniques, 2007, 55(6): 1322-1331. doi: 10.1109/TMTT.2007.897777
[7]	Xiong Run, Chen Bin, Yin Qin, et al. Improved formalism for the FDTD analysis of thin-slot penetration by equivalence principle[J]. IEEE Antennas & Wireless Propagation Letters, 2011, 10(10): 655-657.
[8]	Wu C T, Pang Y H, Wu R B. An improved formalism for FDTD analysis of thin-slot problems by conformal mapping technique[J]. IEEE Trans Antennas and Propagation, 2003, 51(9): 2530-2533. doi: 10.1109/TAP.2003.816382
[9]	孙大伟, 俞集辉. 屏蔽分析中的三维FDTD细孔缝模型[J]. 电工技术学报, 2006, 21(10): 7-11. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS200610002.htm Sun Dawei, Yu Jihui, A 3D thin slot model by FDTD for shielding analysis, Transactions of China Electrotechnical Society, 2006, 21(10): 7-11 https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS200610002.htm
[10]	方明江, 刘强, 闫丽萍, 等. 含三维复杂工程细缝金属腔的电磁屏蔽效能评估[J]. 强激光与粒子束, 2018, 30: 073201. doi: 10.11884/HPLPB201830.180047 Fang Mingjiang, Liu Qiang, Yan Liping, et al. Evaluation of electromagnetic shielding effectiveness for metallic enclosure with complex thin slots. High Power Laser and Particle Beams, 2018, 30: 073201 doi: 10.11884/HPLPB201830.180047
[11]	Li Hanyu, Zhou Haijing, Liu Yang, et al. Massively parallel FDTD program JEMS-FDTD and its applications in platform coupling simulation[C]//IEEE International Symposium on Electromagnetic Compatibility. 2014.
[12]	Cao Xiaolin, Zhang Aiqing, Liu Qingkai. Software quality assurance for the development of JASMIN infrastructure[C]//IEEE International Conference on Software Engineering & Applications. 2015.
[13]	莫则尧, 张爱清. 并行自适应结构网格应用支撑软件框架(JASMIN2.0版)用户指南[G]. 2011. Mo Zeyao, Zhang Aiqing. User guide of J parallel adaptive structured mesh applications infrastructure(JASMIN 2.0). 2011
[14]	张青洪, 廖成, 李瀚宇, 等. 基于JASMIN框架的抛物方程有限差分解法并行计算及其应用[J]. 强激光与粒子束, 2015, 27: 083204. doi: 10.11884/HPLPB201527.083204 Zhang Qinghong, Liao Cheng, Li Hanyu, et al. Parallel computing of finite difference algorithm for parabolic equation based on JASMIN and its application. High Power Laser and Particle Beams, 2015, 27: 083204 doi: 10.11884/HPLPB201527.083204