Nonlinear optimization for longitudinal beam injection in diffraction-limited synchrotron light sources
-
摘要:
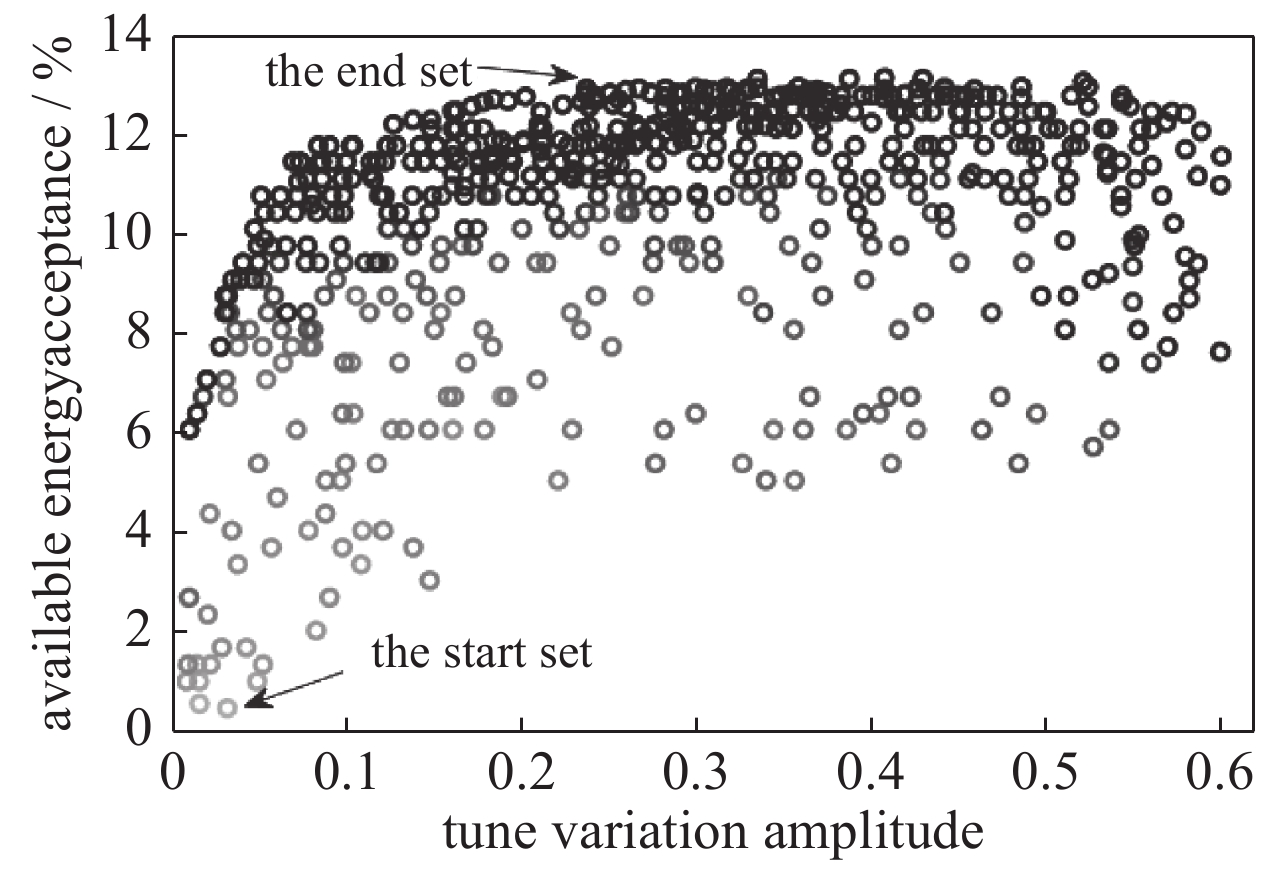
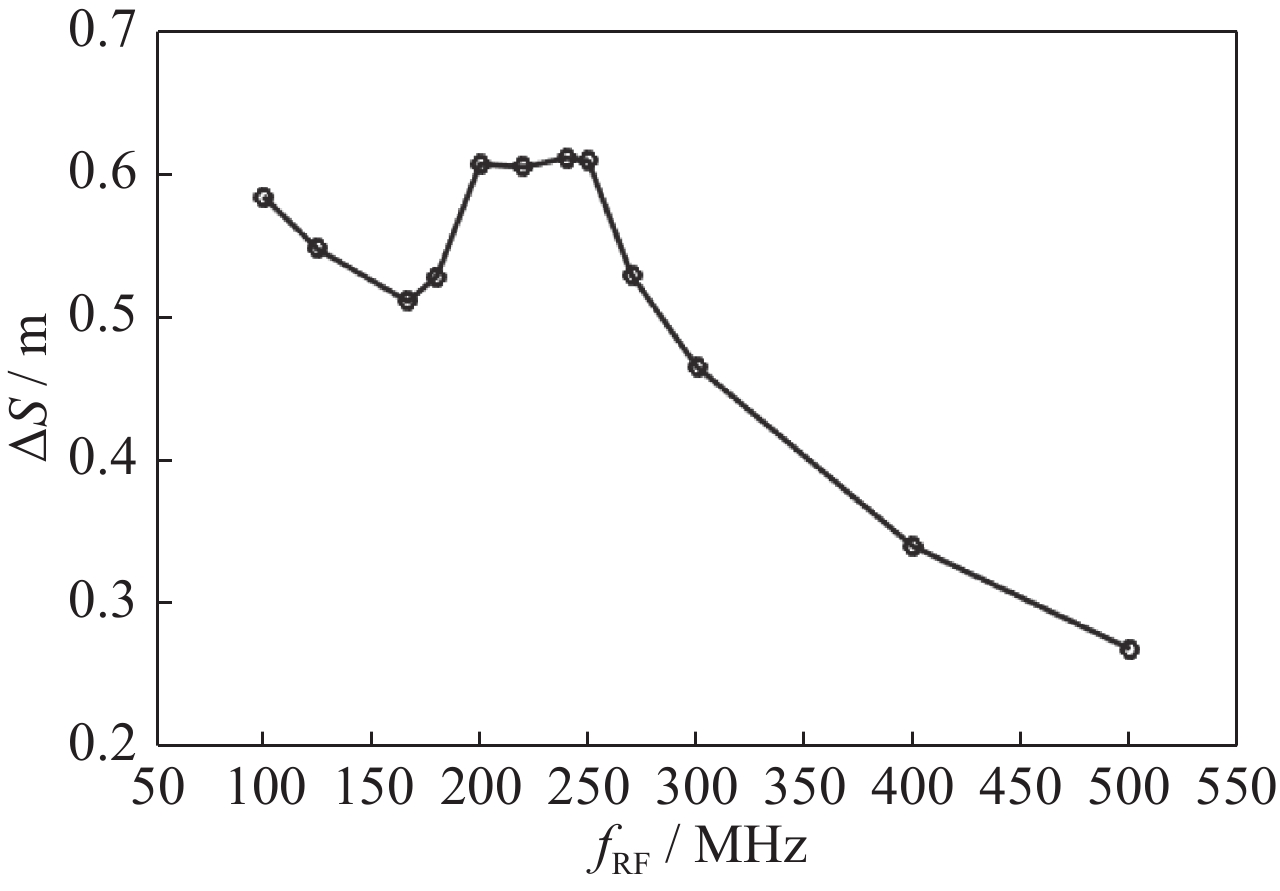
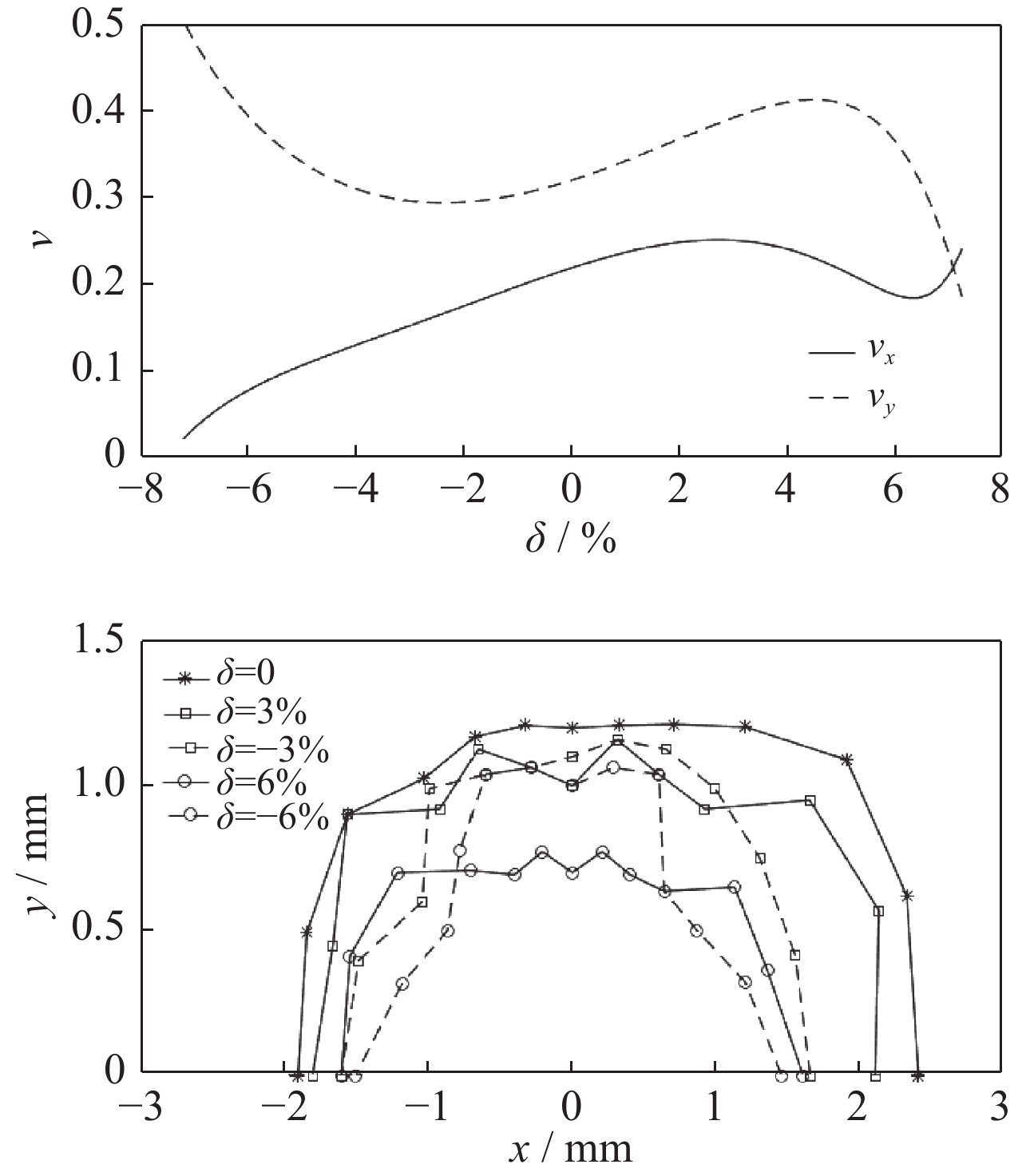
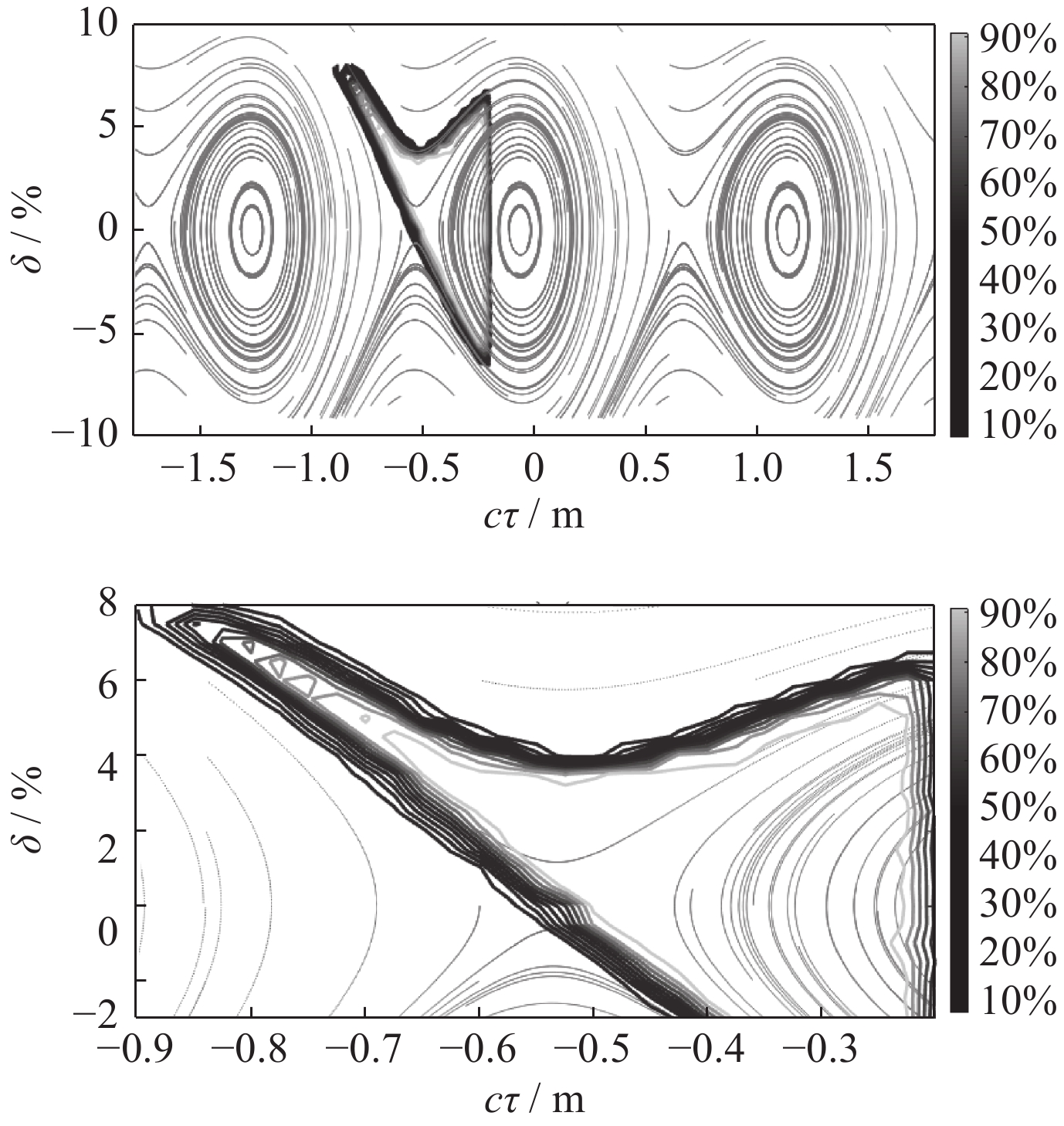
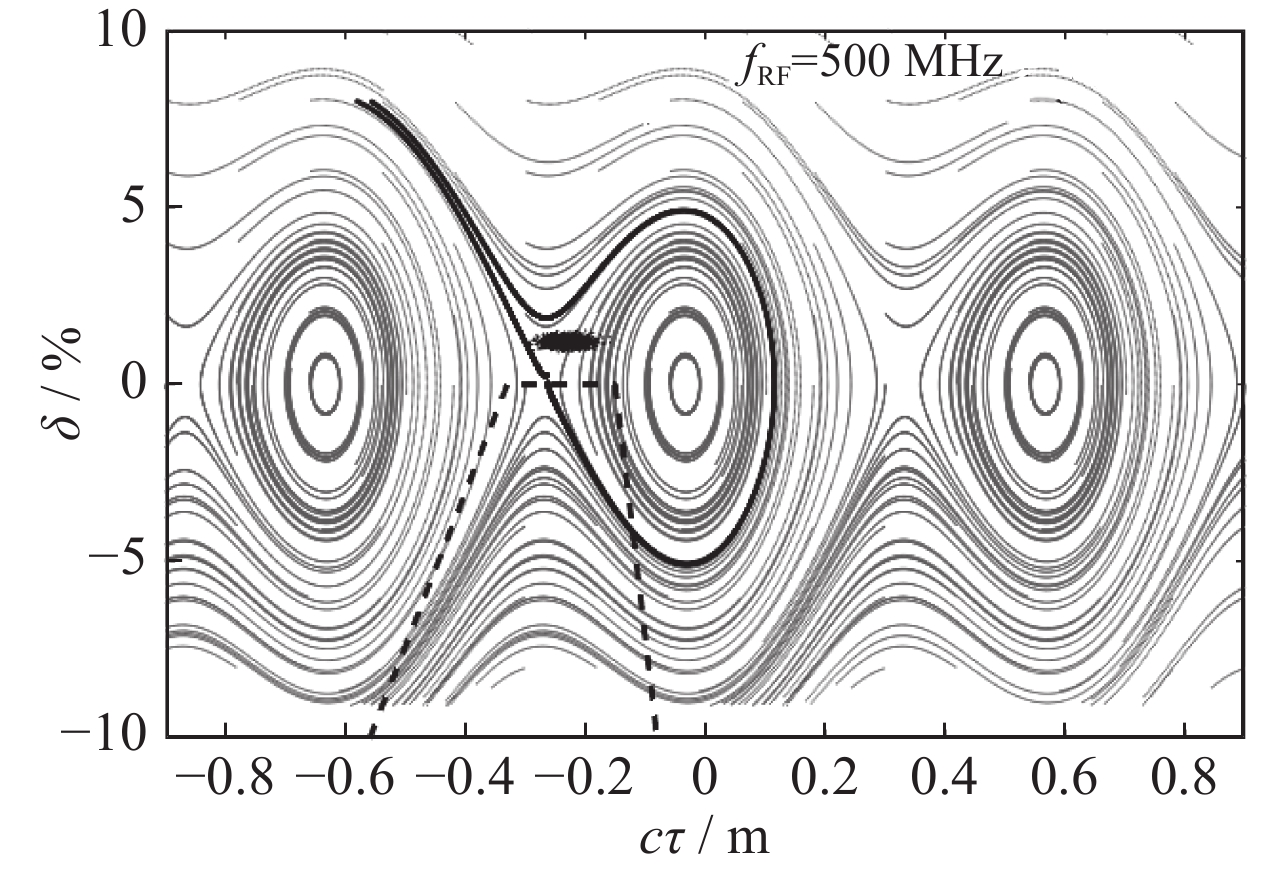
下一代同步辐射光源储存环动力学孔径较小,因而束流注入困难,可以通过纵向束流注入解决这一问题。为了使用更长的kicker脉冲,有必要降低高频频率以增加注入束流到储存束流的时移。因为同步辐射运动,时移更长的束流有更高的动量偏差,所以通过该方法进行注入需要储存环提供足够大的能量接受度和动力学孔径。用SSRF-U的候选磁聚焦结构来展示纵向束流注入非线性优化的可行方法。由一系列高频频率的最佳结果可知,低于界限频率时kicker脉冲不会继续增长。在束流模拟中,采用界限频率与合适六级铁强度,可使SSRF-U储存环束流注入达到最高效率。
Abstract:Storage rings of the next generation synchrotron light sources have quite small dynamic apertures with which transverse beam injection can hardly be efficient. The longitudinal beam injection may be a solution to this problem. To apply a longer kicker pulse, it is necessary to increase time offset of the injected beam to the stored one by reducing RF frequency. The beam with a longer time offset will have a higher momentum deviation due to synchrotron motion, thus full injection of this method requires the storage ring to provide large enough energy acceptance and off-momentum dynamic aperture. A candidate lattice of the upgraded Shanghai Synchrotron Radiation Facility (SSRF-U) was used to nonlinearly optimize the longitudinal beam injection. With the optimal results of a series of RF frequencies, it is found that there is a critical RF frequency below which lowering frequency could not help to lengthen the kicker pulse in a given lattice. The beam injection into the SSRF-U storage ring was simulated and reached high efficiency with its critical RF frequency and optimal sextupole gradients.
-
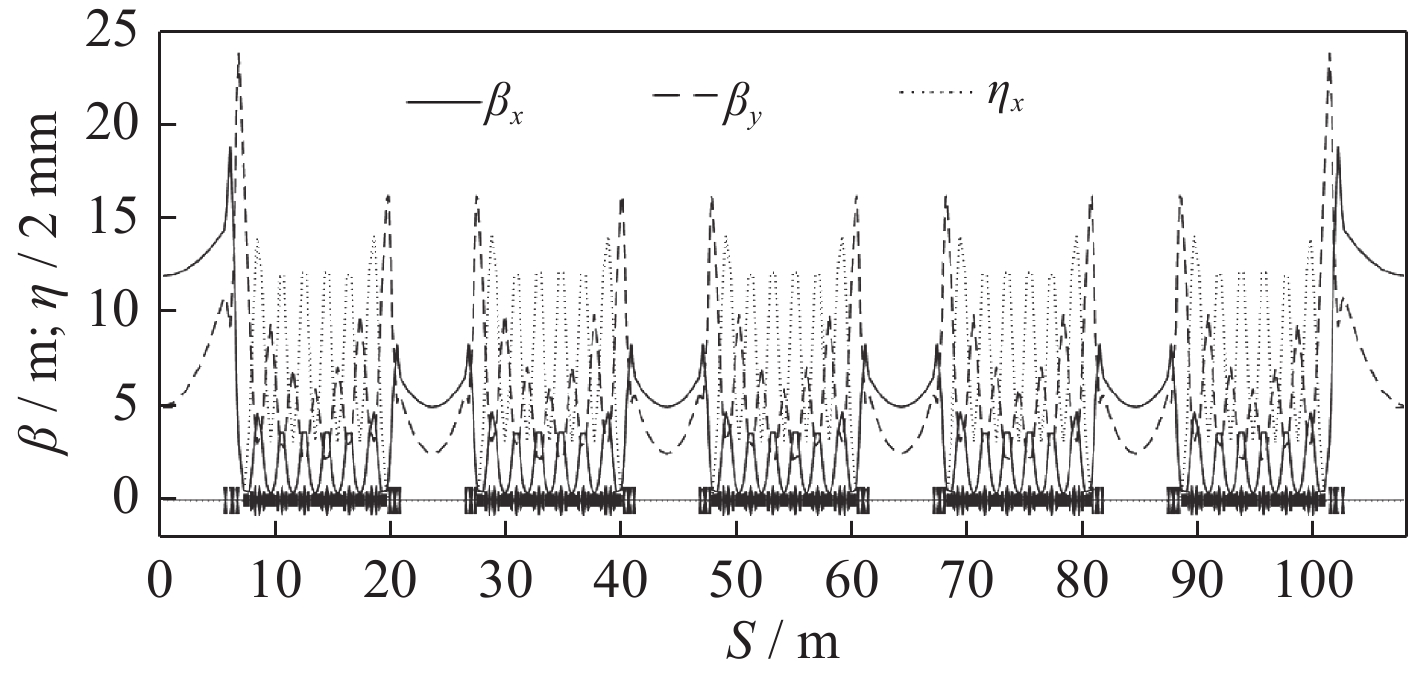
Table 1. The lattice parameters of the SSRF-U storage ring
lattice 20×7BA beam energy/GeV 3.0 circumference/m 432 tune (H, V, S) 61.22, 15.32, 0.001 64 natural chromaticity (H, V) −129.2, −81.04 corrected chromaticity (H, V) 2.0, 2.0 momentum compaction factor 0.000 1 damping partition number (H, V, S) 1.374, 1.000, 1.626 damping time (H, V, S)/ms 12.29, 16.89, 10.39 energy loss per turn/keV 512.0 natural energy spread 7.616×10−4 natural emittance/(pm·rad) 97.00 RF voltage/MV 1.50 -
[1] Hettel R. DLSR design and plans: an international overview[J]. Journal of Synchrotron Radiation, 2014, 21: 843-855. doi: 10.1107/S1600577514011515 [2] Einfeld D, Plesko M, Schaper M. First multi-bend achromat lattice consideration[J]. Journal of Synchrotron Radiation, 2014, 21: 856-861. doi: 10.1107/S160057751401193X [3] Borland M, Decker G, Emery L, et al. Lattice design challenges for fourth-generation storage-ring light sources[J]. Journal of Synchrotron Radiation, 2014, 21: 912-936. doi: 10.1107/S1600577514015203 [4] Li H H, Liu G M, Zhang W Z. The injection system of the SSRF storage ring[C]//Proceedings of EPAC08. 2008: 2076-2078. [5] Harada K, Kobayashi Y, Miyajima T, et al. New injection scheme using a pulsed quadrupole magnet in electron storage rings[J]. Physical Review Special Topics− Accelerators and Beams, 2007, 10: 123501. doi: 10.1103/PhysRevSTAB.10.123501 [6] Takaki H, Nakamura N. Beam injection with a pulsed sextupole magnet in an electron storage ring[J]. Physical Review Special Topics−Accelerators and Beams, 2010, 13: 020705. doi: 10.1103/PhysRevSTAB.13.020705 [7] Yamamoto N, Zen H, Hosaka M, et al. Beam injection with pulsed multipole magnet at UVSOR-III[J]. Nuclear Instruments and Methods in Physics Research A, 2014, 767: 26-33. doi: 10.1016/j.nima.2014.07.059 [8] Borland M. Simulation of swap-out reliability for the advanced photon source upgrade[C]//Proceedings of NAPAC2016. 2016: 881-883. [9] Steier C, Anders A, Luo T, et al. On-axis swap-out R&D for ALS-U[C]//Proceedings of IPAC2017. 2017: 2821-2823, [10] Aiba M, Boge M, Marcellini F, et al. Longitudinal injection scheme using short pulse kicker for small aperture electron storage rings[J]. Physical Review Special Topics−Accelerators and Beams, 2015, 18: 020701. doi: 10.1103/PhysRevSTAB.18.020701 [11] Hernandez A S, Aiba M. Investigation of the injection scheme for SLS 2.0[C]//Proceedings of IPAC2015. 2015: 1720-1723. [12] Jiang B C, Zhao Z T, Tian S Q, et al. Using a double-frequency RF system to facilitate on-axis beam accumulation in a storage ring[J]. Nuclear Instruments and Methods in Physics Research A, 2016, 814: 1-5. doi: 10.1016/j.nima.2016.01.024 [13] Collier P. Synchrotron phase space injection into LEP[C]//Proceedings of PAC1995. 1995: 551-553. [14] Jiao J, Duan Z. Statistical analysis of the limitation of half integer resonances on the available momentum acceptance of the High Energy Photon Source[J]. Nuclear Instruments and Methods in Physics Research A, 2017, 841: 97-103. doi: 10.1016/j.nima.2016.10.037 [15] Zhao Z T, Xu H J, Ding H. Commissioning of the Shanghai Light Source[C]//Proceedings of PAC09. 2009: 55-59. [16] Zhao Z T, Yin L X, Leng Y B, et al. Consideration on the future major upgrades of the SSRF storage ring[C]//Proceedings of IPAC2015. 2015: 1672-1674. [17] Tian S Q. Lattice design and optimization of the SSRF storage ring with super-bend[J]. Nuclear Science and Techniques, 2014, 25: 010102. doi: 10.13538/j.1001-8042/nst.25.010102 [18] Terebilo A. Accelerator toolbox for MATLAB[R]. SLAC-PUB-8732, 2001. [19] Leemann S C, Andersson A, Eriksson M, et al. Beam dynamics and expected performance of Sweden’s new storage-ring light source: MAX IV[J]. Physical Review Special Topics−Accelerators and Beams, 2009, 12: 120701. doi: 10.1103/PhysRevSTAB.12.120701 [20] Raimondi P. The ESRF low emittance upgrade[C]//Proceedings of IPAC2016. 2016: 2023-2027. [21] Xu G, Duan Z, Guo Y Y, et al. Recent physical studies for the HEPS project[C]//Proceedings of IPAC2016. 2016: 2886-2888. [22] Tian S Q, Zhang M Z, Zhang Q L, et al. Lattice design of the SSRF-U storage ring[C]//Proceedings of IPAC2015. 2015: 304-306. [23] Yu L H. Analysis of nonlinear dynamics by square matrix method[J]. Physical Review Accelerators and Beams, 2017, 20: 034001. doi: 10.1103/PhysRevAccelBeams.20.034001 [24] Bengtsson J. On-line control of the nonlinear dynamics for synchrotrons[J]. Physical Review Special Topics−Accelerators and Beams, 2015, 18: 074002. doi: 10.1103/PhysRevSTAB.18.074002 [25] Yang L Y, Li Y J, Guo W M, et al. Multiobjective optimization of dynamic aperture[J]. Physical Review Special Topics−Accelerators and Beams, 2011, 14: 054001. doi: 10.1103/PhysRevSTAB.14.054001 -




 下载:
下载: