Study of 0.8 THz regenerative feedback oscillators
-
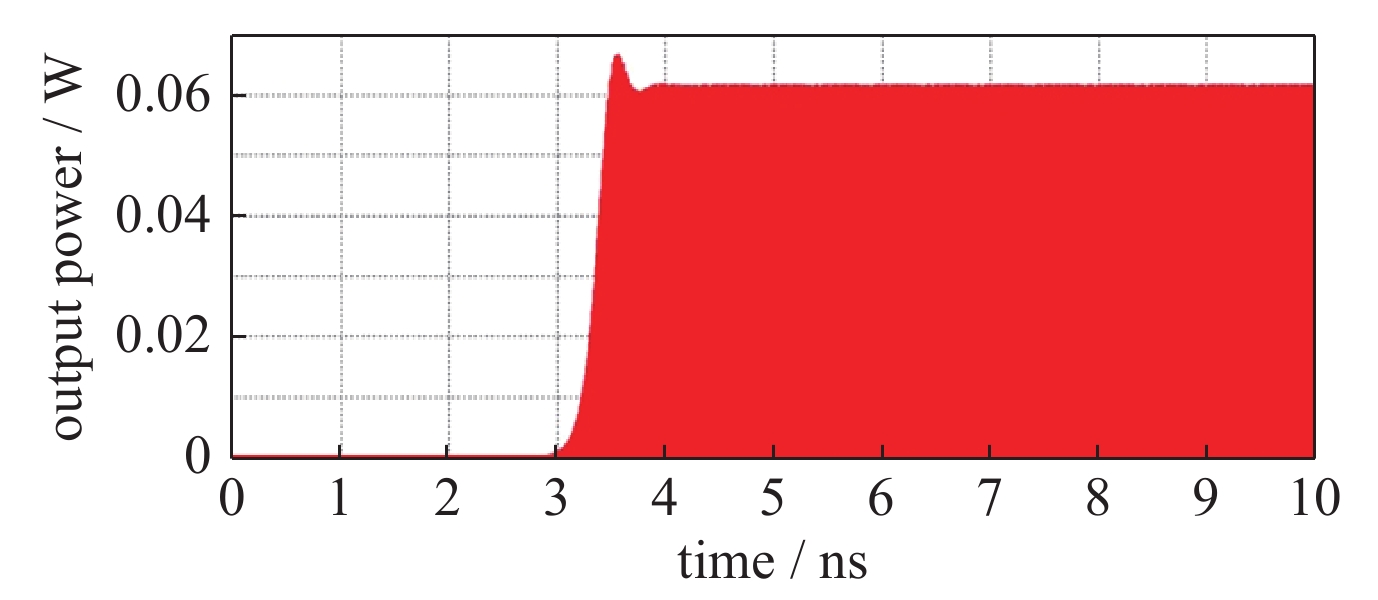
摘要: 随着太赫兹技术的发展,高频率、大功率的太赫兹辐射源一直是国内外研究的热点。再生反馈振荡器作为一种新型太赫兹源器件,具有可行性高、功率大的优点。基于0.8 THz太赫兹波成像系统的需求,采用折叠波导慢波结构,对再生反馈振荡器进行设计与研究。首先对0.8 THz折叠波导慢波结构进行设计并使用CST微波工作室中的本征模求解器进行参数优化,再通过CST粒子工作室中的PIC仿真模块对整管进行热特性仿真,验证了方案的可行性,仿真结果显示,最终可产生60 mW的稳定输出信号。Abstract: With the development of terahertz technology, high-frequency and high-power terahertz radiation sources have been the focus of researching all over the world. Based on the requirement of 0.8 THz terahertz wave imaging system, the regenerative feedback oscillator is designed and studied by using folded waveguide slow wave structure(SWS). In this paper, the SWS of 0.8 THz folded waveguide is designed and optimized by using the eigenmode solver in CST Microwave Studio. Then the oscillator is simulated and verified by PIC solver in CST Particle Studio. In the initial exploration stage of THz, regenerative feedback oscillator has the advantage of high feasibility and high output power. The simulation results show that a stable output signal of 60 mW can be generated.
-
Key words:
- regenerative feedback oscillator /
- terahertz /
- folded waveguide /
- PIC solve
-
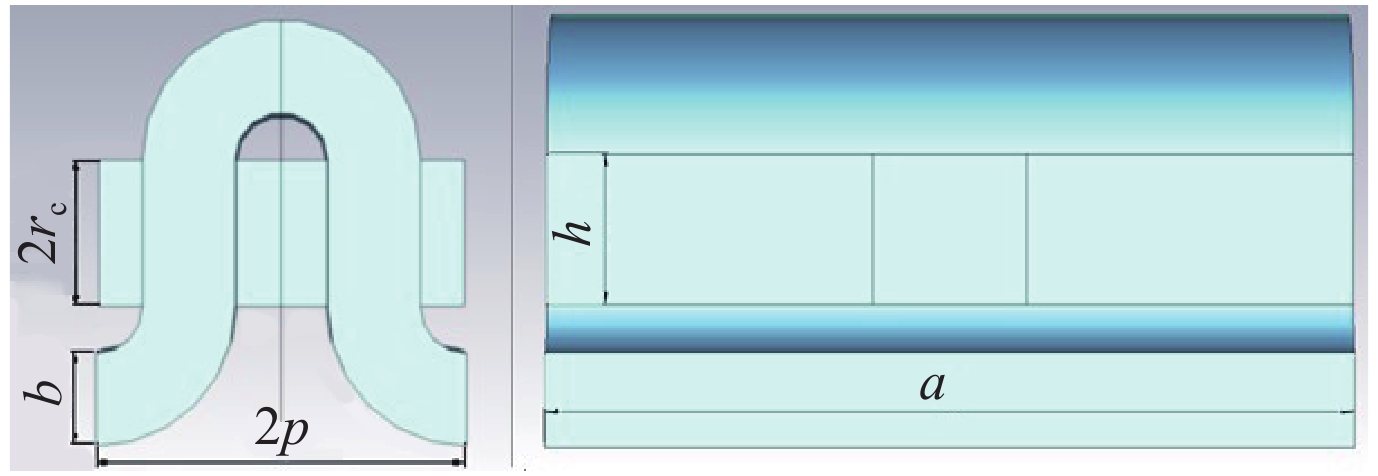
表 1 折叠波导尺寸参数
Table 1. Dimension parameters of folded waveguide
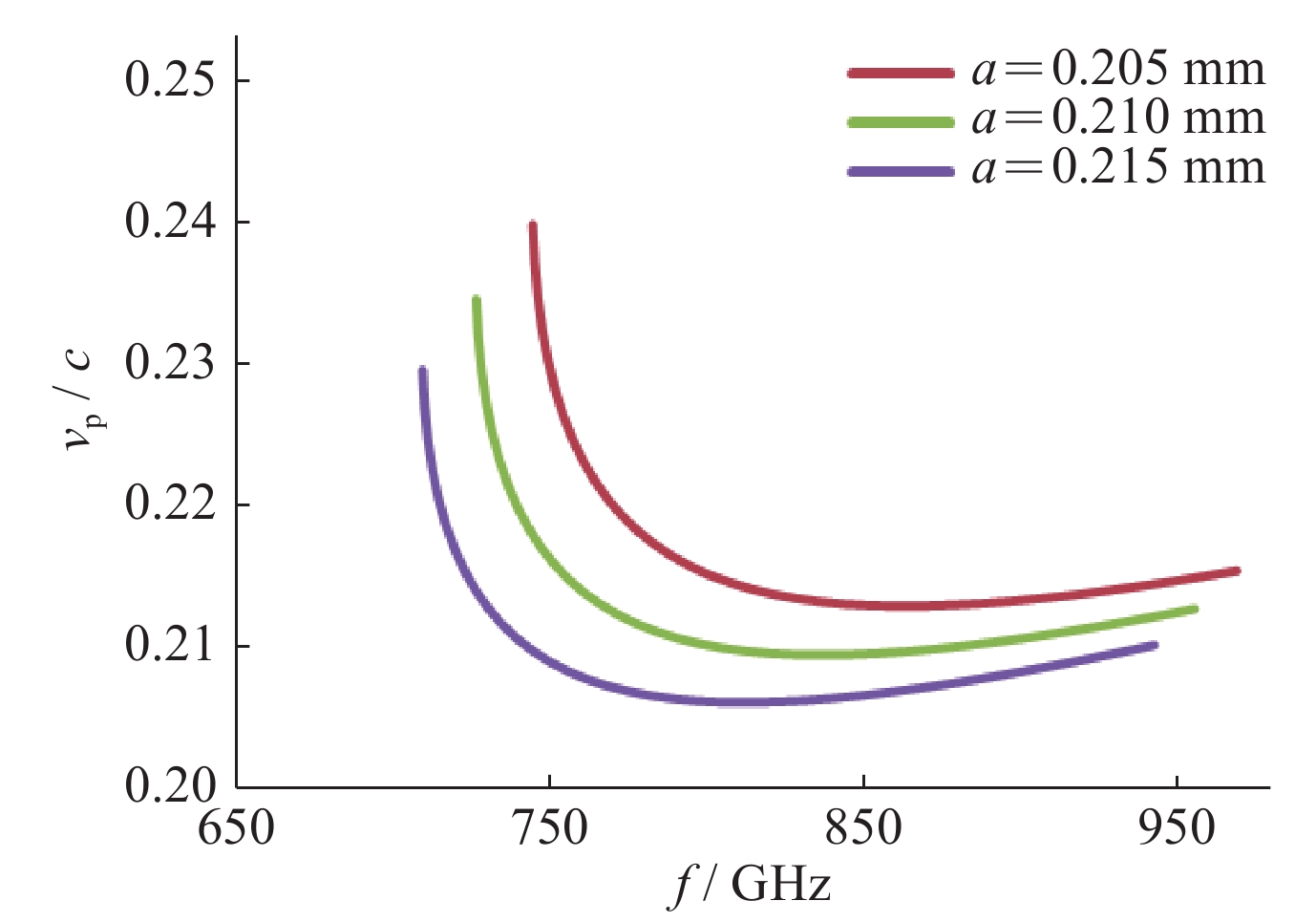
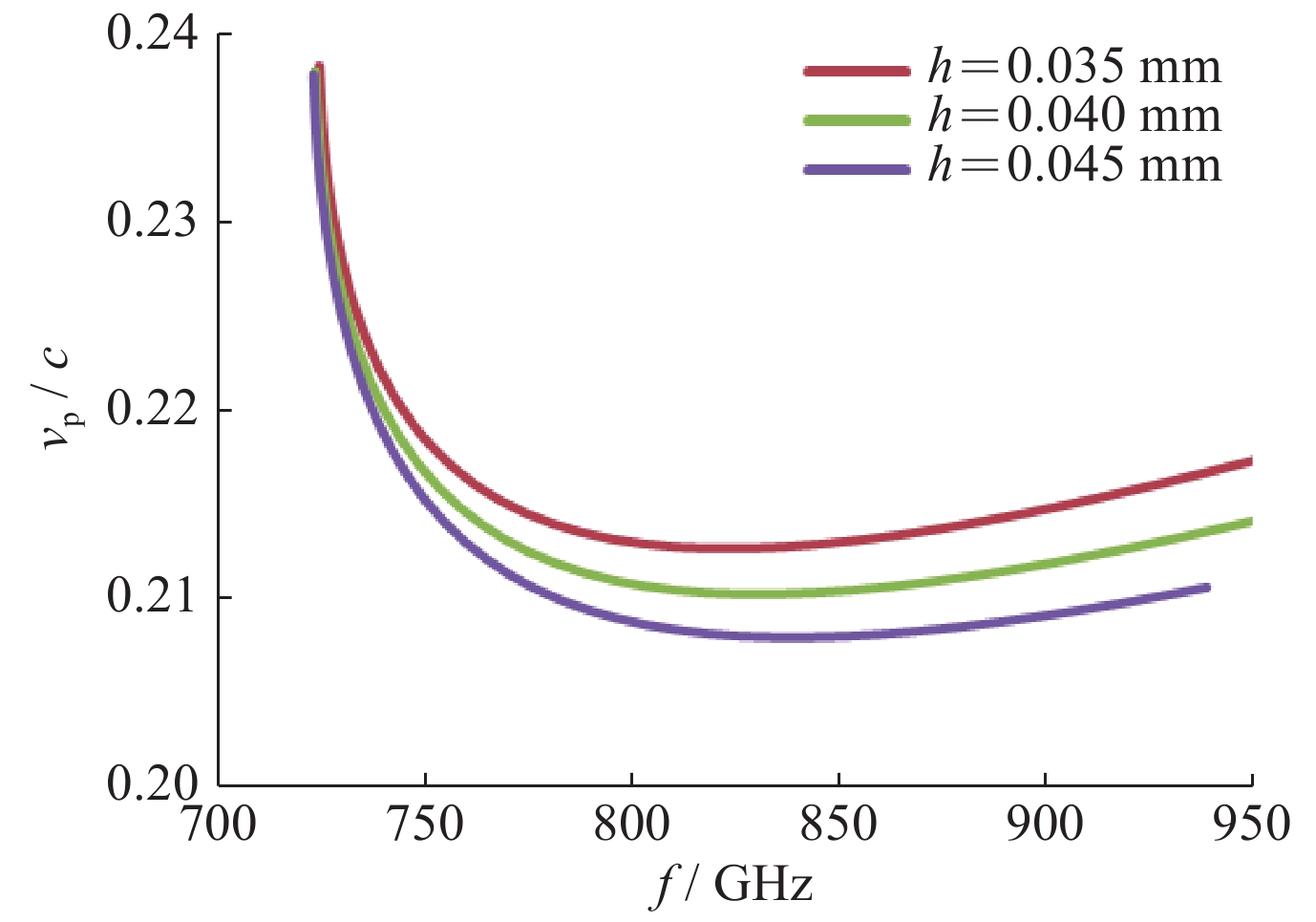
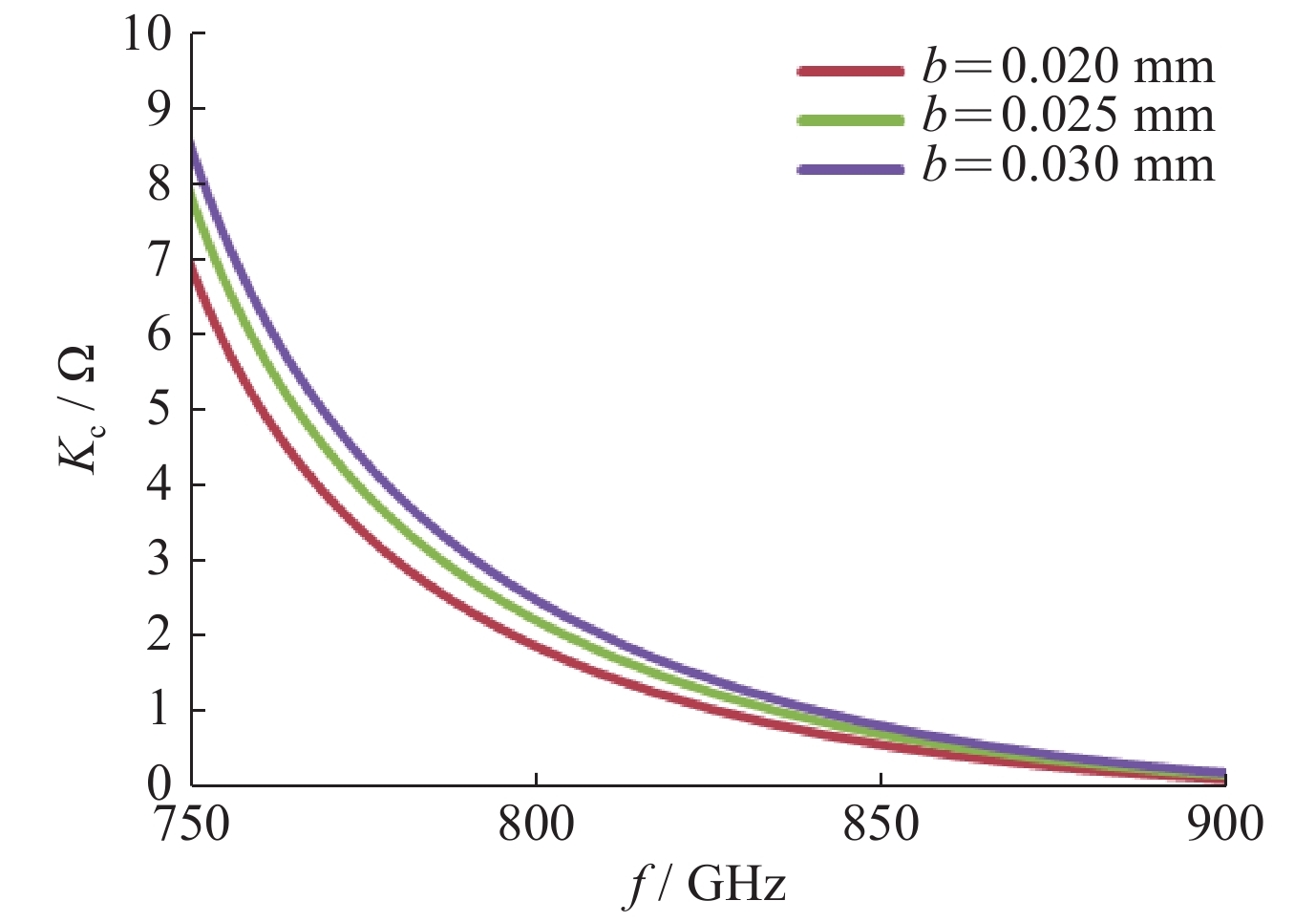
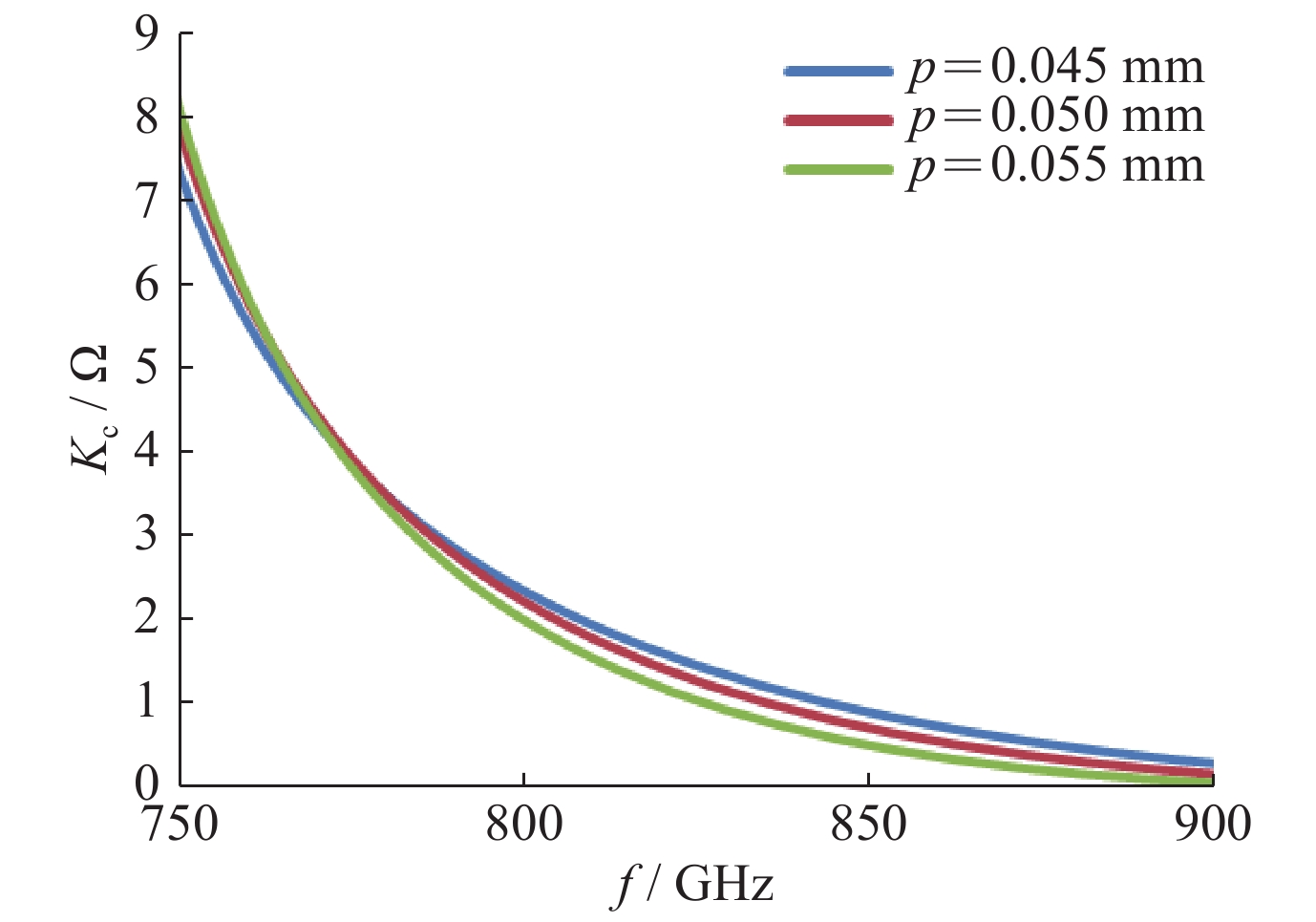
a/mm b/mm h/mm p/mm rc/mm 0.210 0.025 0.040 0.050 0.020 -
Limbach S, Gallagher S, Welter J D, et al. Folded waveguide traveling-wave tube sources for terahertz radiation[J]. IEEE Trans Plasma Science, 2004, 32(3): 1002-1014. doi: 10.1109/TPS.2004.828886 Tucek J, Kreischer K, Gallagher D, et al. Development and operation of a 650 GHz folded waveguide source[C]// IEEE International Vacuum Electronics Conference. 2007. Cai Jun, Hu Yinfu, Wu Xianping, et al. Investigation of THz regenerative oscillator[C]//IEEE International Vacuum Electronics Conference. 2010. 高鹏. 行波管再生反馈振荡器的研究[D]. 成都: 电子科技大学, 2010.Gao Peng. Study on traveling wave tube regenerative feedback oscillators. Chengdu: University of Electronic Science and Technology of China, 2010 Kory C, Ives L, Read M, et al. W-band MEMS-based TWT development[C]//IEEE International Conference on Vacuum Electronics. 2004. 蔡军. W波段折叠波导慢波结构的研究[D]. 济南: 山东大学, 2006.Cai Jun. Study on W-band folded waveguide slow wave structure. Ji’nan: Shandong University, 2006 刘盛纲. 微波电子学导论[M]. 北京: 国防工业出版社, 1985: 349-364.Liu Shenggang. Introduction to microwave electronics. Beijing: National Defence Industry Press, 1985: 349-364 -





 下载:
下载: