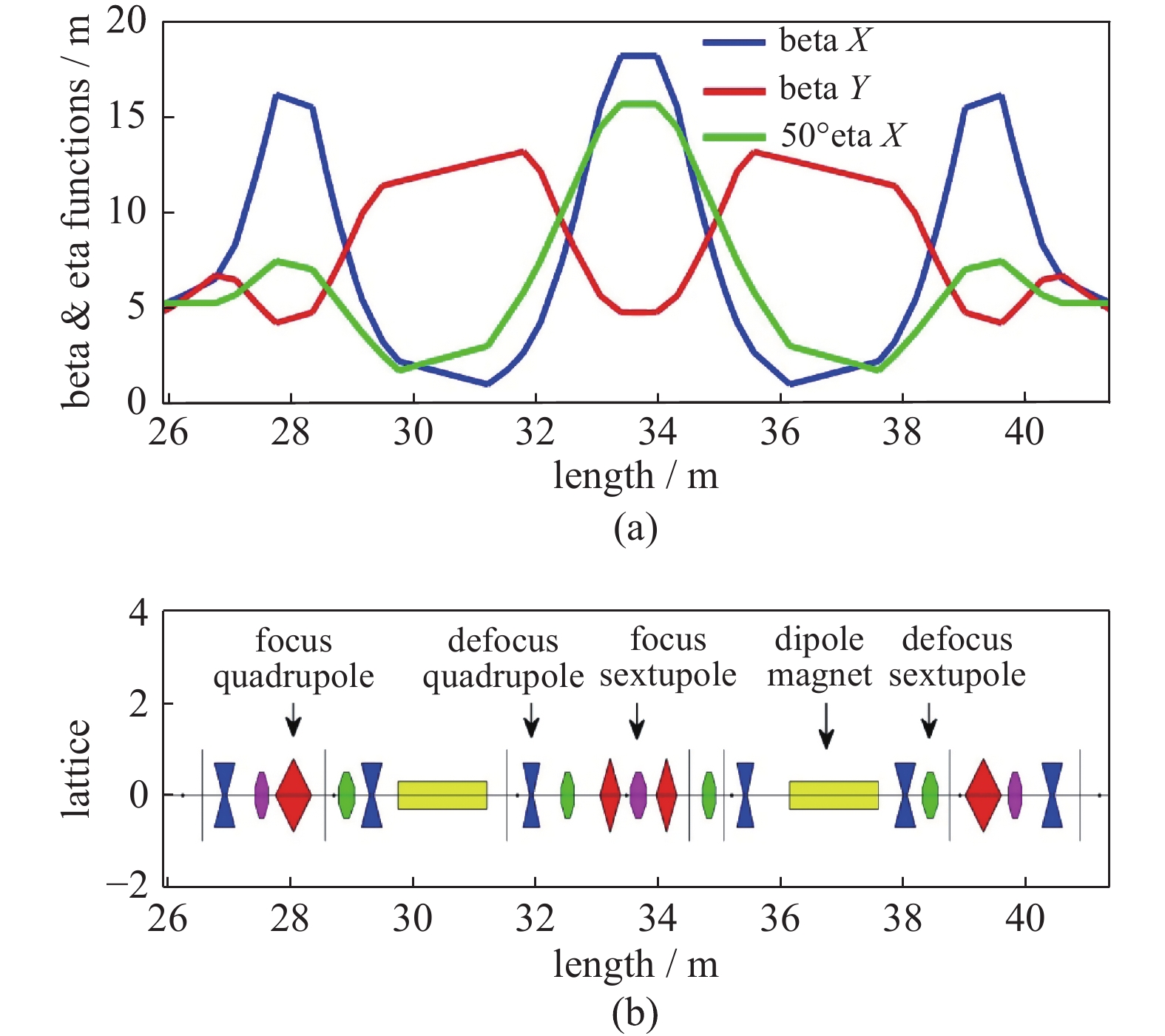
Operation stability improvement for synchrotron light sources by tune feedback system
-
摘要:
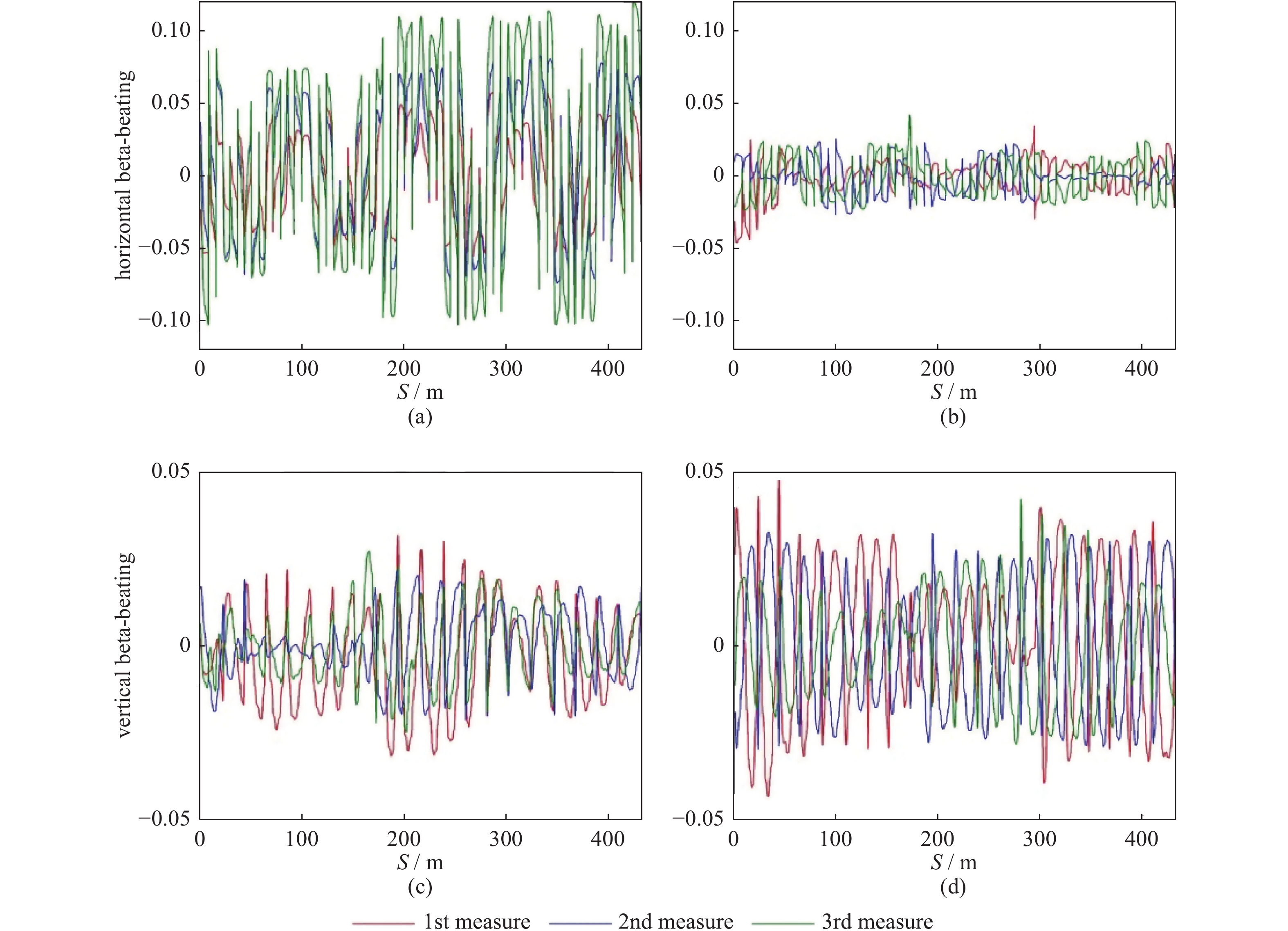
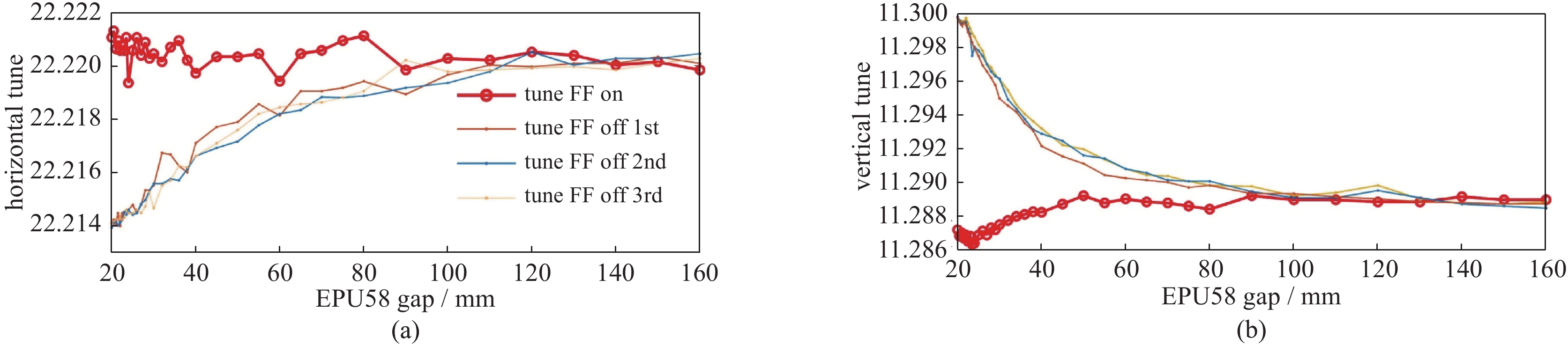
上海同步辐射装置(SSRF)储存环上目前已经安装了十台插入元件(IDs)。在用户时间,插入元件的间隙被反复地调整以进行科学实验。虽然使用了插入件前馈系统,但依然存在扰动束流光学的残余四极场,它会导致束流横向振荡工作点的变化,进而影响机器的性能和同步辐射光亮度的稳定。为此,我们研发了一个工作点反馈系统来解决这个问题,并且已经在上海光源储存环上投入了运行,在两周左右的运行周期内,工作点的稳定度达到了±0.001。这个反馈系统还有另一个重要功能,即可以根据监控反馈系统校正电流的变化趋势来判断二极磁铁电源和四极磁铁电源是否存在慢漂问题。为了验证这个工作点反馈的可行性,我们对使用反馈前后几周的束流参数进行了比较,包括储存环注入效率、束流寿命、水平方向束斑尺寸以及β函数的变化情况(beta-beatings)。
-
关键词:
- 工作点反馈 /
- 稳定性 /
- SSRF /
- 束流光学 /
- beta-beatings
Abstract:Ten Insert Devices (IDs) had been installed in the Shanghai Synchrotron Radiation Facility (SSRF) storage ring. The ID gaps were repeatedly adjusted for the scientific experiments during the user time. The residual quadrupole errors beyond the ID feedforward disturbed the beam optics, including the betatron tune deviations that spoiled machine performance and brightness stability. A tune feedback system was developed and implemented in the SSRF storage ring to resolve the deterioration. The tune stability of ±0.001 in 2 weeks was reached. Another important function of this feedback system is finding out slow drift in the power supplies of dipole or quadrupole by observing the correction current changes in the feedback. To prove this feedback’s feasibility, we compared variations of the beam parameters, including the injection efficiency, the beam life-time, the horizontal beam size and the beta-beatings.
-
Key words:
- tune feedback /
- stability /
- SSRF /
- beam optics /
- beta-beating
-
Table 1. Beam parameters of the SSRF storage ring
parameter design value measured value beam energy / GeV 3.50 3.50 circumference / m 432 --------- number of cells 20 --------- construction DBA --------- numbers of QF/QD in one cell 4/6 --------- beam current / mA 200−300 240 tune (H, V) 22.22, 11.29 22.220, 11.290 (±0.01) natural emittance / nm·rad 3.89 3.9 coupling 1% 0.3% natural chromaticity (H, V) −55.7, −17.9 -------- corrected chromaticity (H, V) --------- 1.5, 2.5 RMS energy spread 9.845×10−4 0.001 energy loss per turn / MeV 1.435 ~1.45 momentum compaction factor 4.27×10−4 4.2 ×10−4 RF voltage / MV 4.0 4~4.8 RF frequency / MHz 499.654 499.68 synchrotron frequency 0.007 2 0.007 5 -
[1] Heron M T, Abbott M G, Furseman M, et al. Feed-forward and feedback schemes applied to the diamond light source storage ring[C]// Proceedings of IPAC2014, 2014: 1757-1759. [2] Martin I P S, Fielder R, Furseman M, et al. Active optics stabilisation measures at the diamond storage ring[C]//Proceedings of IPAC2014, 2014: 1760-1762. [3] Chao A W, Mess K H, Tigner M, et al. Handbook of accelerator physics and engineering[M]. 2nd ed. World Scientific, 2013. [4] Hou Jie, Tian Shunqiang, Zhang Manzhou, et al. Studies of closed orbit correction and slow orbit feedback for the SSRF storage ring[J]. Chinese Physics C, 2009, 33(2): 145-150. [5] Zhang Manzhou, Wang kun, Zhang Qinglei, et al. Compensations of double elliptical polarization undulator effects on the SSRF storage ring[J]. High Power Laser and Particle Beams, 2017, 29: 075103. [6] Tian Shunqiang, Zhang Manzhou, Zhang Qinglei, et al. Lattice design of the SSRF-U storage ring[C]// Proceedings of IPAC2015, 2015: 304-306. [7] Dai Zhimin, Liu Guimin, Huang Nan. Design of the SSRF storage ring magnet lattice[J]. Nuclear Science and Techniques, 2003, 14(2): 89-92. [8] Zhang Wenzhi, Tian Shunqiang, Zhang Manzhou, et al. Design and first commissioning of a new mode with lower emittance in the SSRF storage ring[J]. Chinese Physics C, 2009, 33(5): 397-400. doi: 10.1088/1674-1137/33/5/016 [9] Tomás R, Aiba M, Franchi A, et al. Review of linear optics measurement and correction for charged particle accelerators[J]. Physical Review Accelerators and Beams, 2017, 20(5): 054801. doi: 10.1103/PhysRevAccelBeams.20.054801 [10] Tian Shunqiang, Zhang Wenzhi, Li Haohu, et al. Linear optics calibration and nonlinear optimization during the commissioning of the SSRF storage ring[J]. Chinese Physics C, 2009, 33(s2): 83-85. [11] Tian Shunqiang, Hou Jie, Chen Guangling, et al. Analysis of sextupole effects on β function beating in the SSRF storage ring[J]. Chinese Physics C, 2008, 32(7): 576-579. doi: 10.1088/1674-1137/32/7/013 [12] Terebilo A. Accelerator modeling with MATLAB[C]// Proceedings of the 2001 Particle Accelerator Conference, 2001: 3203-3205. [13] Chen, Jianhui, Zhang Manzhou, Zhao Zhentang. Orbit response matrix analysis and lattice periodicity restoration of the SSRF storage ring[J]. Chinese Physics C, 2009, 33(9): 785-788. doi: 10.1088/1674-1137/33/9/015 [14] Safranek J. Experimental determination of storage ring optics using orbit response measurements[J]. Nuclear Instruments and Methods in Physics Research A, 1997, 388(1/2): 27-36. doi: 10.1016/S0168-9002(97)00309-4 [15] Liu C, Hulsart R, Michnoff R, et al. Weighted SVD algorithm for closed-orbit correction and 10Hz feedback in RHIC[C]//Proceedings of IPAC2012, 2012: 2906-2908. [16] Leng Yongbin, Yan Yingbing, Yuan Renxian, et al. Betatron tune measurement system for Shanghai Synchrotron Radiation Facility storage ring[J]. High Power Laser and Particle Beams, 2010, 22(10): 2412-2416. doi: 10.3788/HPLPB20102210.2412 [17] Zhao Zhentang, Yin Lixin, Zhang Wenzhi, et al. Progress towards top-up operation at SSRF [C]// Proceedings of IPAC2011, Spain, 2011: 3008-3010. [18] Jena S, Yadav S, Agrawal R K, et al. Stabilization of betatron tune in Indus-2 storage[J]. Chinese Physics C, 2014, 38(6): 067002. doi: 10.1088/1674-1137/38/6/067002 [19] Tian Shunqiang, Hou Jie, Chen Guangling, et al. New chromaticity compensation approach and dynamic aperture increase in the SSRF storage ring[J]. Chinese Physics C, 2008, 32(8): 661-664. [20] Safranek J, Portmann G, Terebilo A. MATLAB-based LOCO[C]// The 8th European Particle Accelerator Conference, 2002. [21] Zhou Xuemei. Measurement of optics for the SSRF storage ring in commissioning[J]. Chinese Physics C, 2009, 33(s2): 78-82. -




 下载:
下载: