A parameter optimization method of snubber circuit of thyristor under pulse current working condition
-
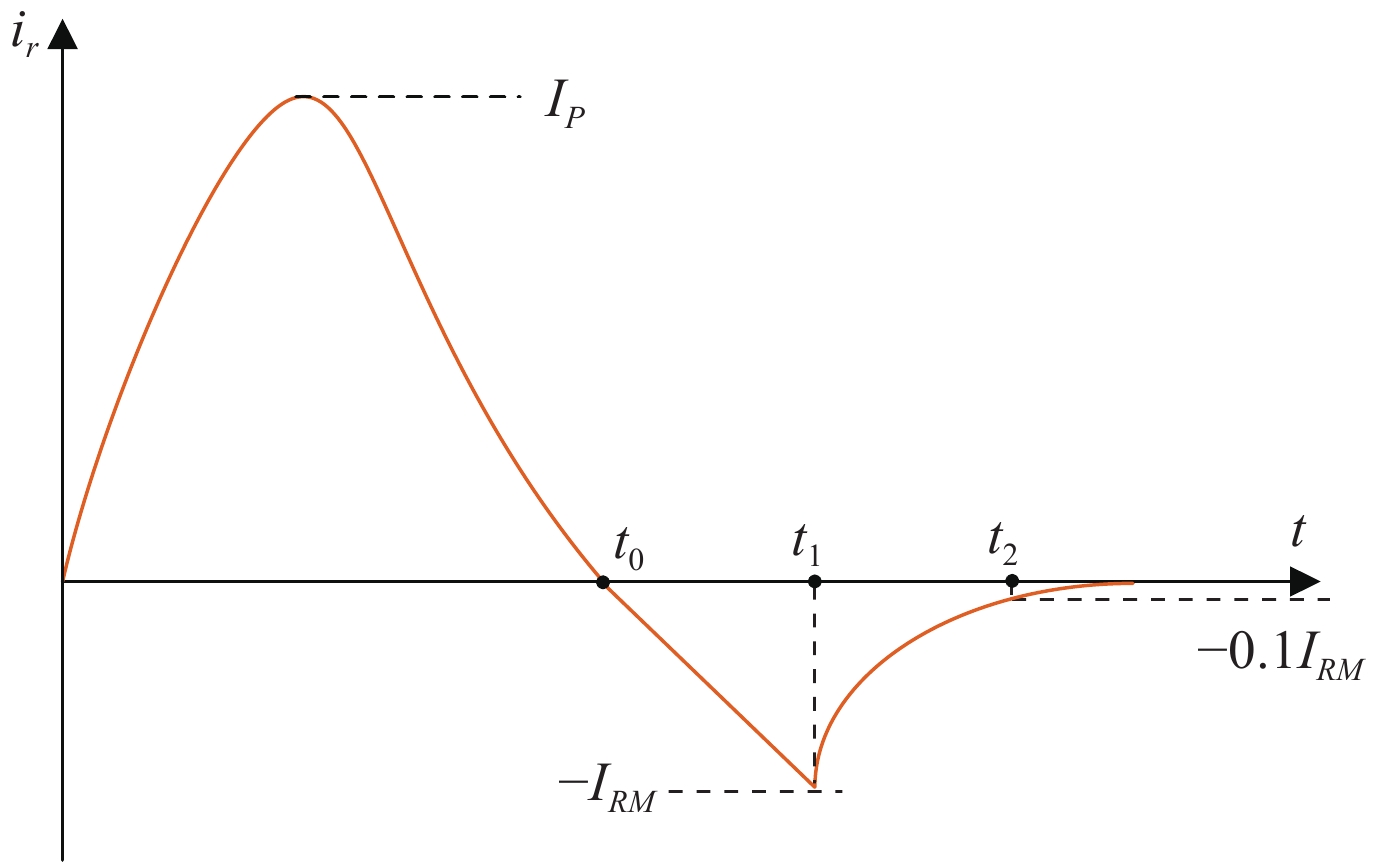
摘要: 对脉冲工况下超导磁体失超保护系统的晶闸管阀组缓冲回路参数进行设计和优化。基于晶闸管反向恢复电流的指数衰减模型建立了晶闸管关断时刻的电流数学模型。通过测试实验获得关键参数之间的关系并结合晶闸管性能及系统要求在Matlab中建立晶闸管电流反向恢复模型。考虑关断时刻电流下降率、反向恢复电压峰值等性能指标要求及回路研制费用,提出了一种脉冲工况下晶闸管缓冲回路的参数设计及优化方法。在Matlab中搭建失超保护系统模型,对比优化前后缓冲回路对系统在晶闸管关断时刻电气性能的影响,仿真结果显示,相比于原参数,最优参数下,反向恢复电压峰值降低了11%,反向恢复电压变化率峰值降低了43%。同时,回路制造成本降低为原先的1/7。Abstract: As thyristor valve is the core equipment of quench protection system of large fusion device, the design and optimization of its snubber circuit parameters are related to the safety and reliability of the valve and even the whole quench protection system. So far, most of the design and optimization of snubber circuit parameters are based on DC steady-state conditions. However, there are few literatures on parameter optimization under impulse conditions. In this paper, the buffer circuit parameters of thyristor valve are designed and optimized under the pulse condition of superconducting magnet quench protection system. Based on the exponential model of thyristor reverse recovery current, the current mathematical model at the turn-off time is established. The relationship between the key parameters is obtained through experiments, and the reverse recovery model of thyristor current is established in Matlab according to thyristor performance and system requirements. Considering the performance requirements such as current drop rate at turn-off time, peak reverse recovery voltage and the cost, a parameter design and optimization method of thyristor snubber circuit under pulse condition is proposed. The model of quench protection system is built in Matlab, the simulation results show that compared with the original parameters, the optimal parameters reduce 11% of the peak reverse recovery voltage and 43% of the peak reverse recovery voltage change rate. At the same time, the manufacturing cost of the circuit is reduced to 1/7 of the original one.
-
Key words:
- quench protection /
- thyristor /
- snubber circuit /
- pulse current
-
表 1 晶闸管反向恢复过程中电气参数数据
Table 1. Specific characteristics of thyristor during reverse recovery process
charge voltage/V Ip/A IRM/A di/dt/ (A·µs−1) Qrr/µC 1 000 6 622 895 37.10 8 057.3 1 500 9 935 967 50.96 8 412.8 2 000 13 250 1 100 76.54 9 049.2 2 500 16 560 1 206 97.41 9 568.7 3 000 19 880 1 330 121.22 10 153.0 3 500 23 190 1 402 135.97 10 505.4 4 000 26 500 1 523 160.26 11 076.2 4 500 29 810 1 627 179.44 11 517.1 5 000 33 160 1 738 198.98 11 962.4 5 500 36 480 1 846 221.88 12 471.5 6 000 39 790 1 915 238.76 12 849.6 6 500 43 090 2 014 256.90 13 244.7 7 000 46 380 2 132 279.01 13 715.9 7 500 49 880 2 230 298.37 14 122.1 表 2 RC缓冲回路设计要求
Table 2. Design specification of RC snubber circuit for QPS in LSTF
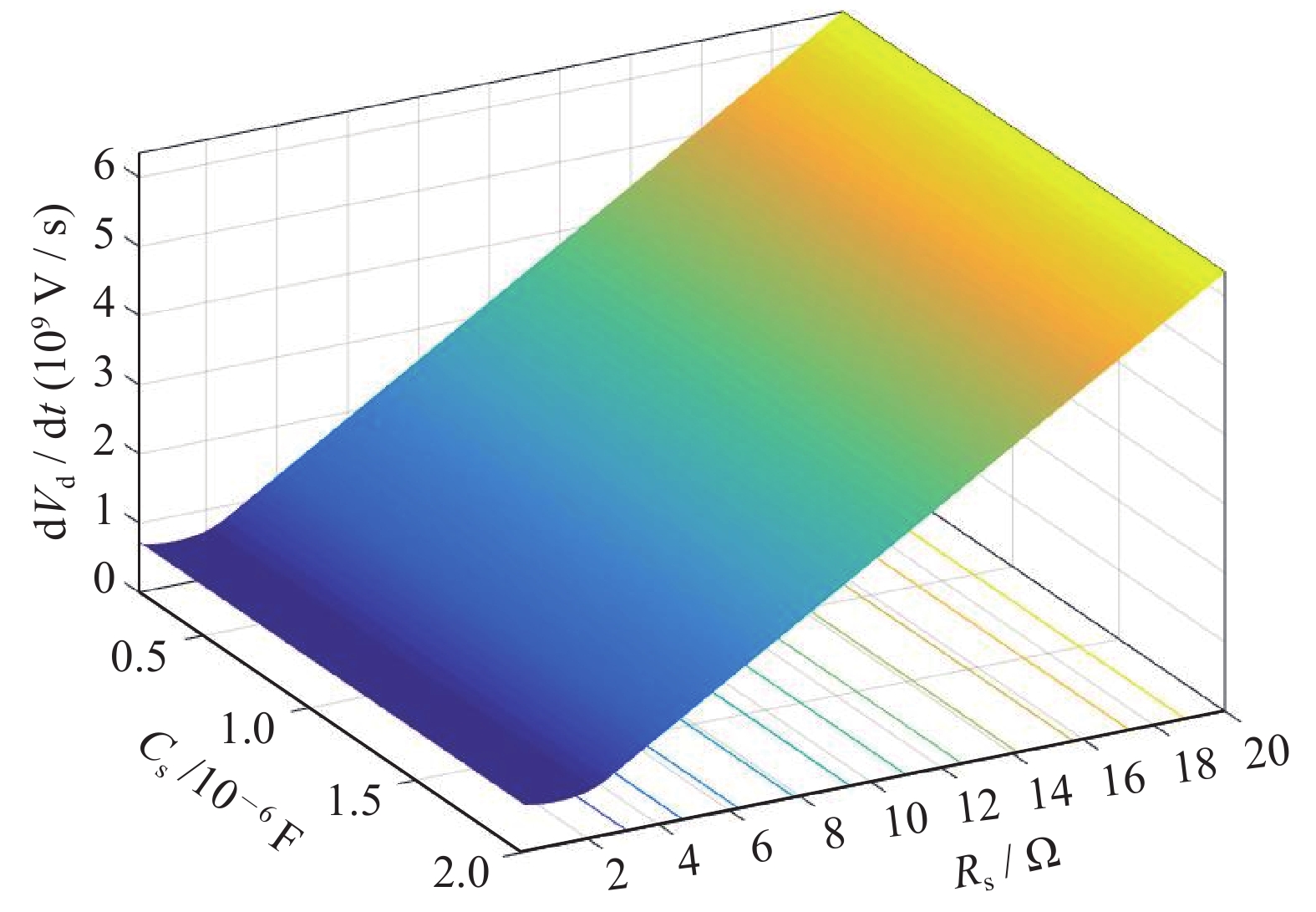
symbol parameter value L/µH external inductance 25 VdRM, VRRM/V max. repetitive peak forward and reverse blocking voltage of chosen thyristor 5 200 dVd/dtcrit/(V·µs-1) critical rate of rise of commutating voltage of chosen thyristor(di/dt=500 A/µs, Tvj=125 ℃) 3 000 IRM/A peak value of reverse recovery current (di/dt=500 A/µs, Tvj=125 ℃) 1 825.7 NS thyristor series number 2 表 3 RC的最优参数及对应的电压特性
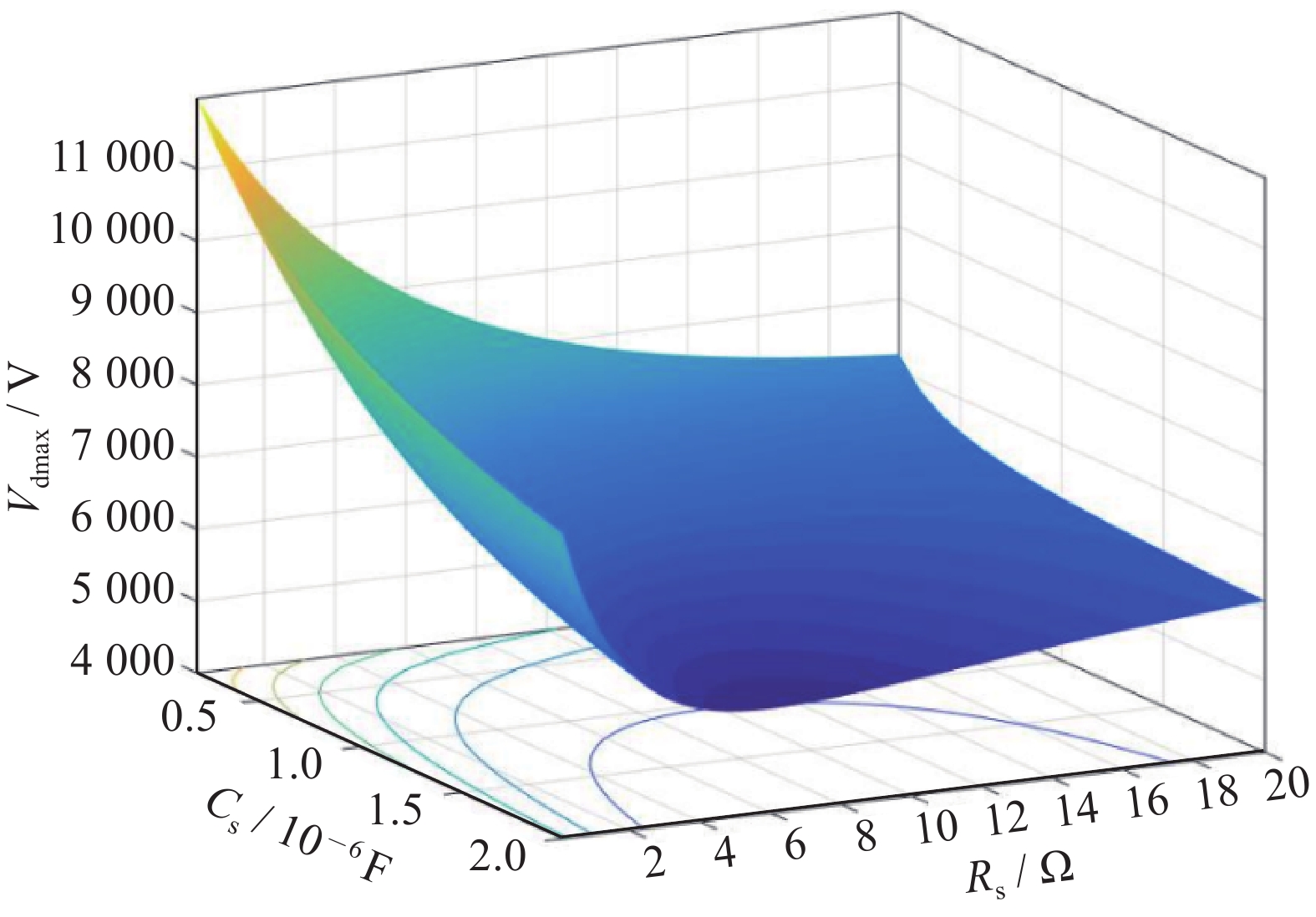
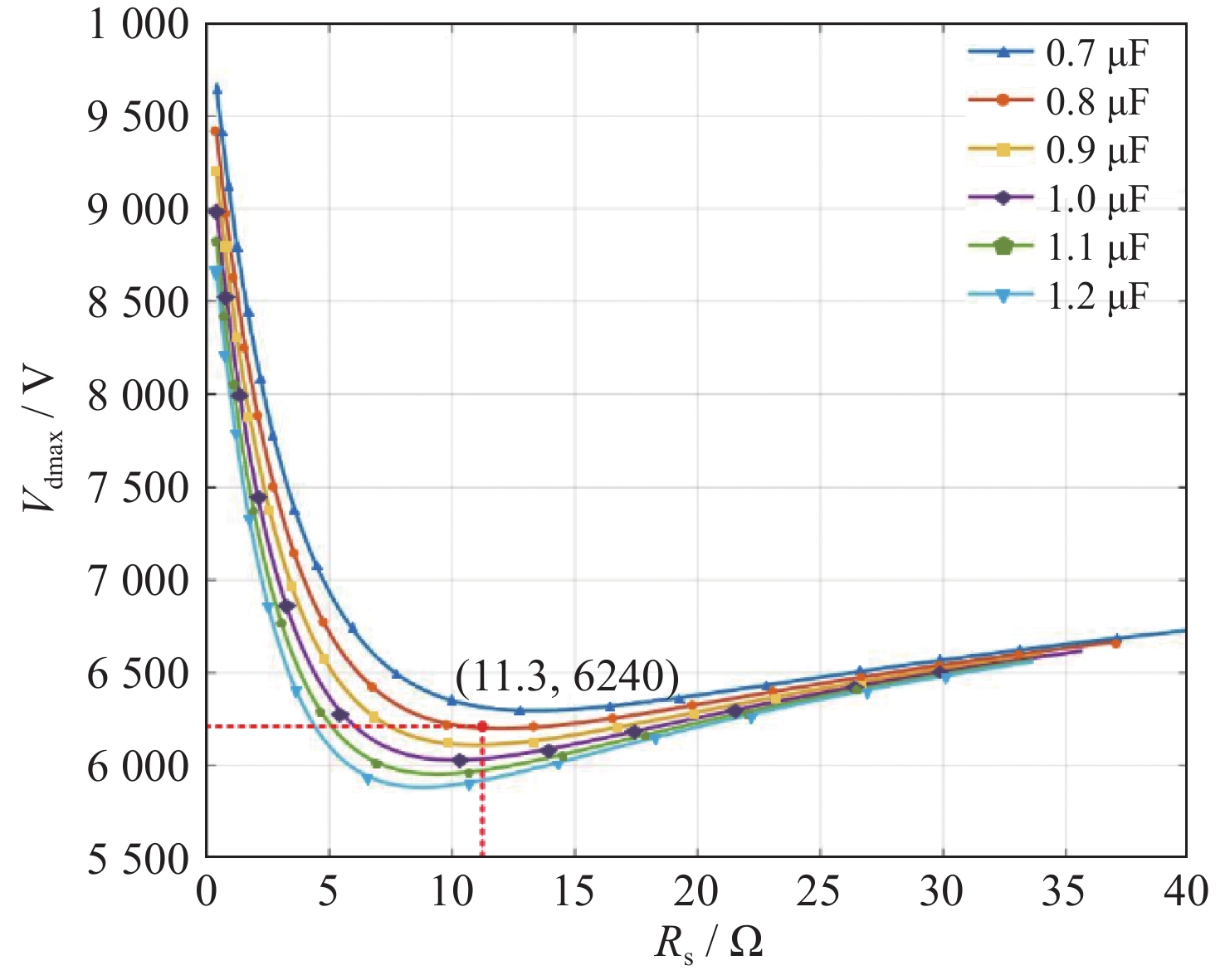
Table 3. The optimum Rs, Cs and corresponding circuit parameters
symbol parameter value Rs/Ω Snubber Resistance 11.3 Cs/μF Snubber Capacitance 0.8 Vdmax/V Maximum Reverse Recovery Voltage 6 210 (dVd/dt)max/(V·μs−1) Maximum Vd change rate 3 600 表 4 电气参数对比
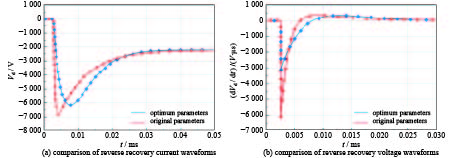
Table 4. Comparison of electrical parameters
optimum parameters Practical parameters IRM /A) 1 815 1 835 (di/dt)0/(A·s-1) 309×106 307×106 vdmax/V 6 168 6 960 (dVd/dt)max /(V·µs-1) 3 598 6 285 -
[1] Song Yuntao, Li Jiangang, Wan Baonian, et al. Concept design of CFETR tokamak machine[J]. IEEE Trans Plasma Science, 2014, 42(3): 503-509. doi: 10.1109/TPS.2014.2299277 [2] 李华, 宋执权, 汪舒生, 等. 核聚变装置中直流保护开关的研究进展[J]. 中国电机工程学报, 2016, 36:233-239. (Li Hua, Song Zhiquan, Wang Shusheng, et al. Study on DC protection switch for superconducting coils in magnetic confinement fusion device[J]. Proceedings of the CSEE, 2016, 36: 233-239 [3] Ren Yong, Zhu Jiawu, Gao Xiang, et al. Electromagnetic, mechanical and thermal performance analysis of the CFETR magnet system[J]. Nuclear Fusion, 2015, 55: 093002. doi: 10.1088/0029-5515/55/9/093002 [4] Wang Shusheng, Song Zhiquan, Fu Peng, et al. Conceptual design of bidirectional hybrid dc circuit breaker for quench protection of the CFETR[J]. IEEE Trans Applied Superconductivity, 2018, 46(5): 1497-1502. [5] 李世平, 任亚东, 熊思宇, 等. 150 mm高压脉冲功率晶闸管的研制与应用[J]. 大功率变流技术, 2012, 1(13):13-16. (Li Shiping, Ren Yadong, Xiong Siyu, et al. Development and application of 150 mm high-voltage pulse power thyristors[J]. Control and Information Technology, 2012, 1(13): 13-16 [6] 董汉彬. 功率晶闸管的暂态热特性研究及应用[D]. 武汉: 华中科技大学, 2012.Dong Hanbin. Research and application on instantaneous thermal characteristic of power thyristors. Wuhan: Huazhong University of Science and Technology, 2012 [7] 岳珂, 刘隆晨, 孙玮, 等. 反向恢复特性在高功率晶闸管检测试验中的应用[J]. 高电压技术, 2017, 43(1):103-109. (Yue Ke, Lu Longchen, Sun Wei, et al. Application of reverse recovery characteristics in high power thyristor testing[J]. High Voltage Engineering, 2017, 43(1): 103-109 [8] 宋执权. EAST超导托卡马克极向场电源失超保护系统的研制[D]. 北京: 中国科学院研究生院, 2007.Song Zhiquan. Research and development of quench protection system in poloidal field power supply system for EAST super-conductive TOKAMAK. Beijing: Graduate University of Chinese Academy of Sciences, 2007 [9] 温家良, 汤广福, 查鲲鹏, 等. 高压晶闸管阀运行试验方法与试验装置的研究与开发[J]. 电网技术, 2006, 32(21):26-31. (Wen Jialiang, Tang Guangfu, Zha Kunpeng, et al. Operational test method of high voltage thyristor valves and development of its synthetic test equipment[J]. Power System Technology, 2006, 32(21): 26-31 doi: 10.3321/j.issn:1000-3673.2006.21.006 [10] Lou Lifang, Liou J J. An improved compact model of silicon-controlled rectifier (SCR) for electrostatic discharge (ESD) applications[J]. IEEE Trans Electron Devices, 2008, 55(12): 3517-3524. doi: 10.1109/TED.2008.2006739 [11] 戴玲, 田书耘, 金超亮, 等. 脉冲功率晶闸管反向恢复特性[J]. 强激光与粒子束, 2016, 28:115001. (Dai Ling, Tian Shuyun, Jin Chaoliang, et al. Reverse recovery characteristics of pulse power thyristor[J]. High Power Laser and Particle Beams, 2016, 28: 115001 [12] Lee C W, Park S B. Design of a thyristor snubber circuit by considering the reverse recovery process[J]. IEEE Trans Power Electronics, 1988, 42(3): 503-509. -




 下载:
下载: