Thermal analysis calculation of dry-type transformer in PSM high voltage power supply
-
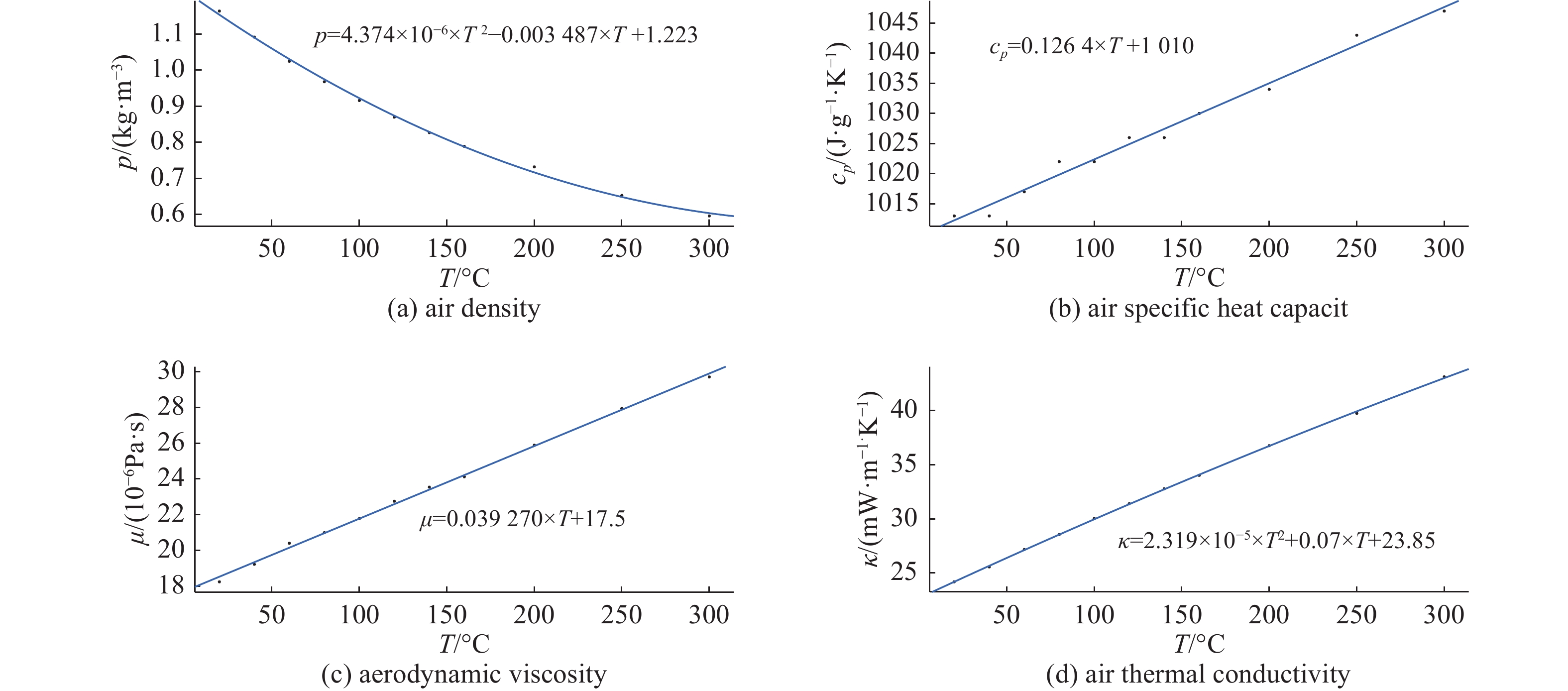
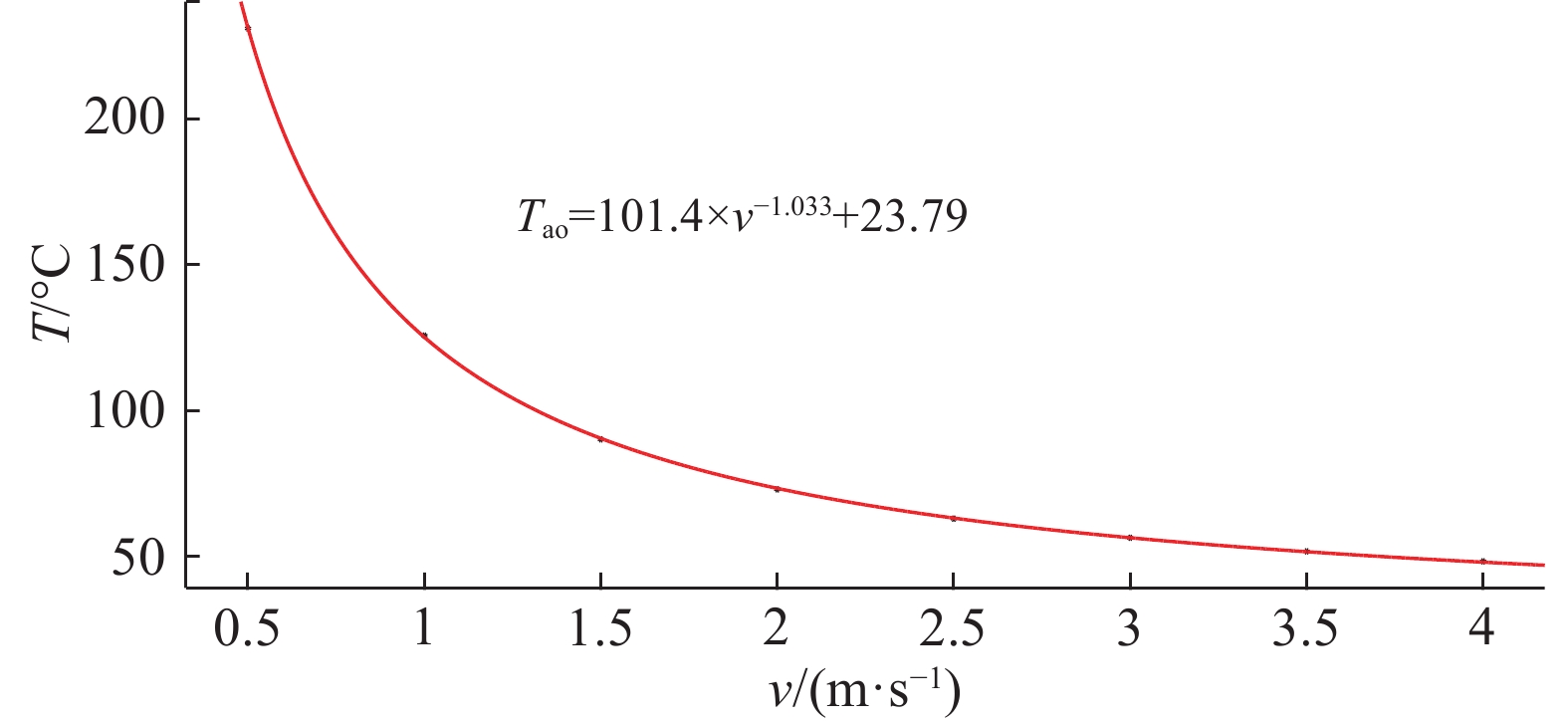
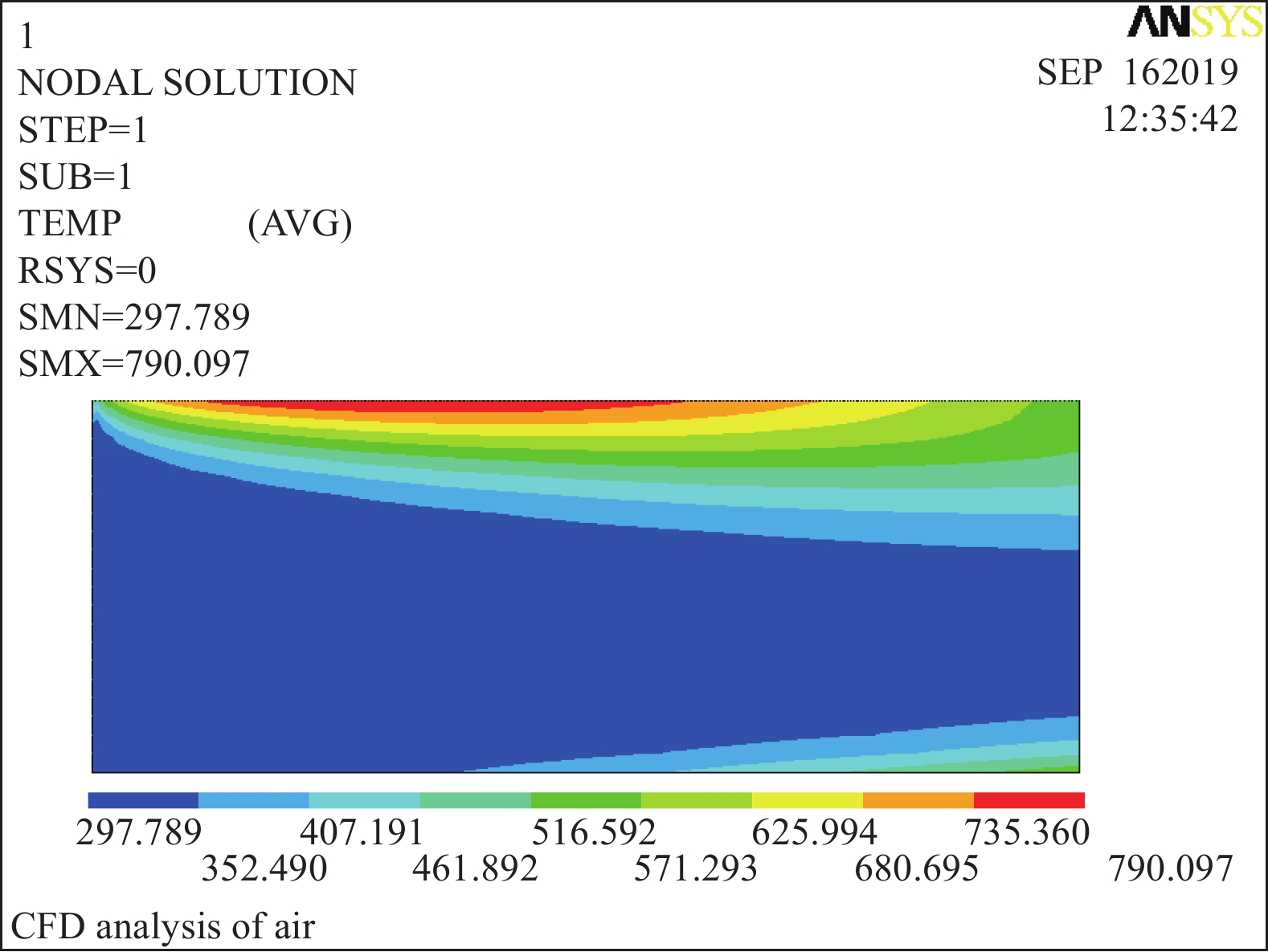
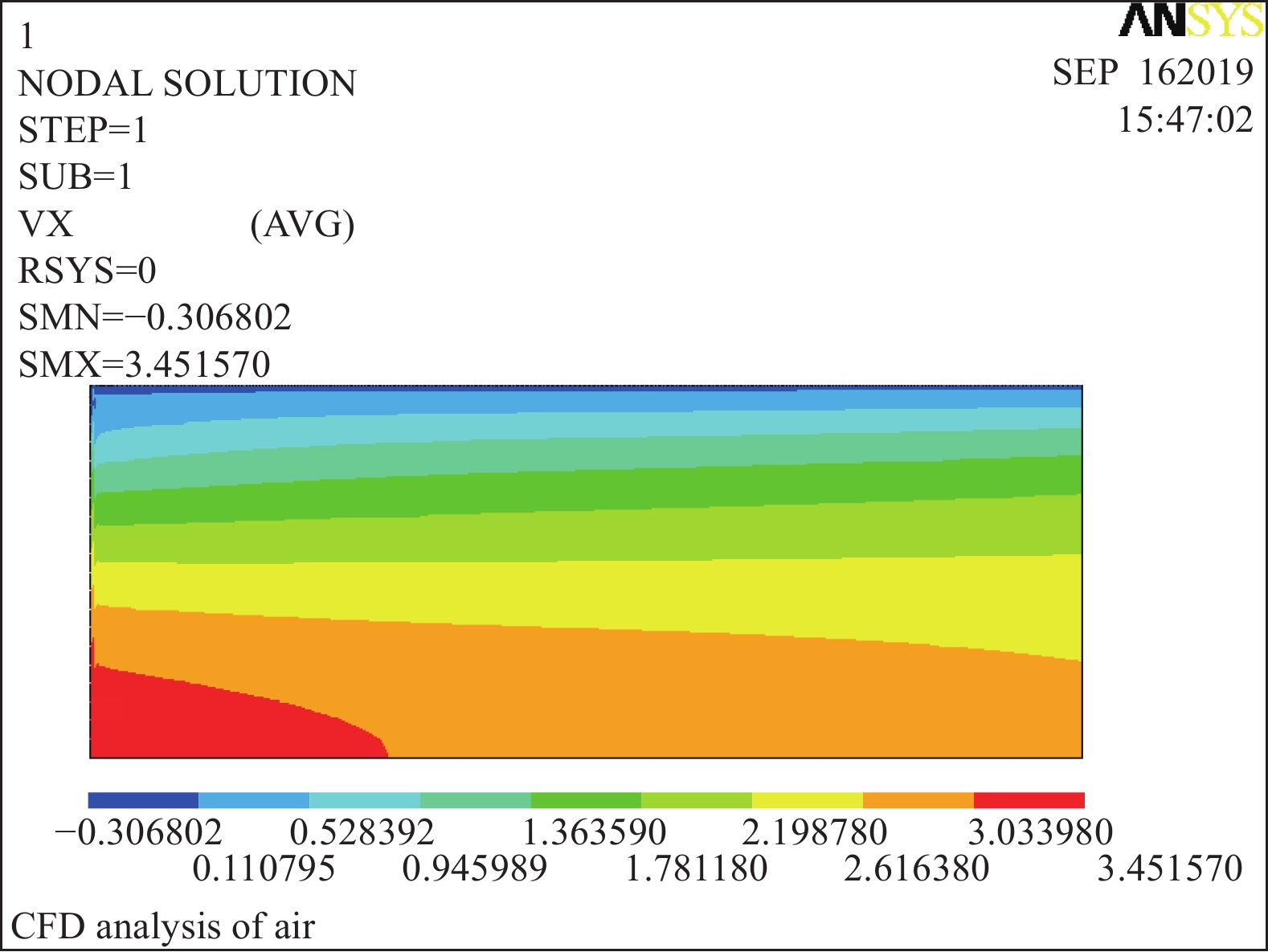
摘要: 多绕组干式整流变压器作为托卡马克装置加热系统中高压电源的一个重要设备,其性能优良与否直接关系到高压电源的输出品质。开展变压器的功率损耗与散热分析研究,减少变压器因温度上升造成的性能影响,对保证变压器的良好工作状态是十分重要的。通过MATLAB对干空气下的比热容、传热系数等热物理性质与温度的关系进行拟合分析,得到相关的关系方程,对变压器的对流传热与热辐射进行分析计算,得到仅在空气自然对流和热辐射的情况下,不能使变压器的温度控制在满足性能的温度范围之内。在强迫空气对流的情况下,实现了变压器良好的散热。进一步利用ANSYS对变压器的温度场分布进行分析,利用温度场的分布趋势图观察强迫风冷相对于自然冷却的优点,强迫风冷降低了整体的温度,使热量更快地散发到周围大气中,减少了变压器受高温的危害。Abstract: Multi-winding dry rectifier transformer is an important equipment for high voltage power supply in Tokamak heating system. Its excellent performance is directly related to the output quality of high voltage power supply. Carrying out research on power loss and heat dissipation of transformers, reducing the performance impact of transformers due to temperature rise, is very important to ensure the good working condition of the transformer. In this paper, the relationship between thermophysical properties and temperature is fitted by MATLAB. The convective heat transfer and thermal radiation of the transformer are analyzed and calculated by the equations. In the case of natural convection and heat radiation of the air, the temperature of the transformer cannot be controlled within a temperature range that satisfies the performance, and the temperature rise is about 200 ℃. In the case of forced air convection, the good heat dissipation of the transformer is realized, and finally the forced air cooling at a wind speed of 2 m/s is achieved, and the temperature rise of the transformer is less than 75 ℃, ensuring the good working condition of the transformer. The article further uses ANSYS to analyze the temperature field distribution of the transformer. Forced air cooling reduces the overall temperature and allows heat to be released to the surrounding atmosphere more quickly, reducing the damage of the transformer under high temperature.
-
Key words:
- dry-type transformer /
- fitting analysis /
- forced convection /
- ANSYS /
- temperature field
-
表 1 变压器的基本参数
Table 1. Basic parameters of the transformer
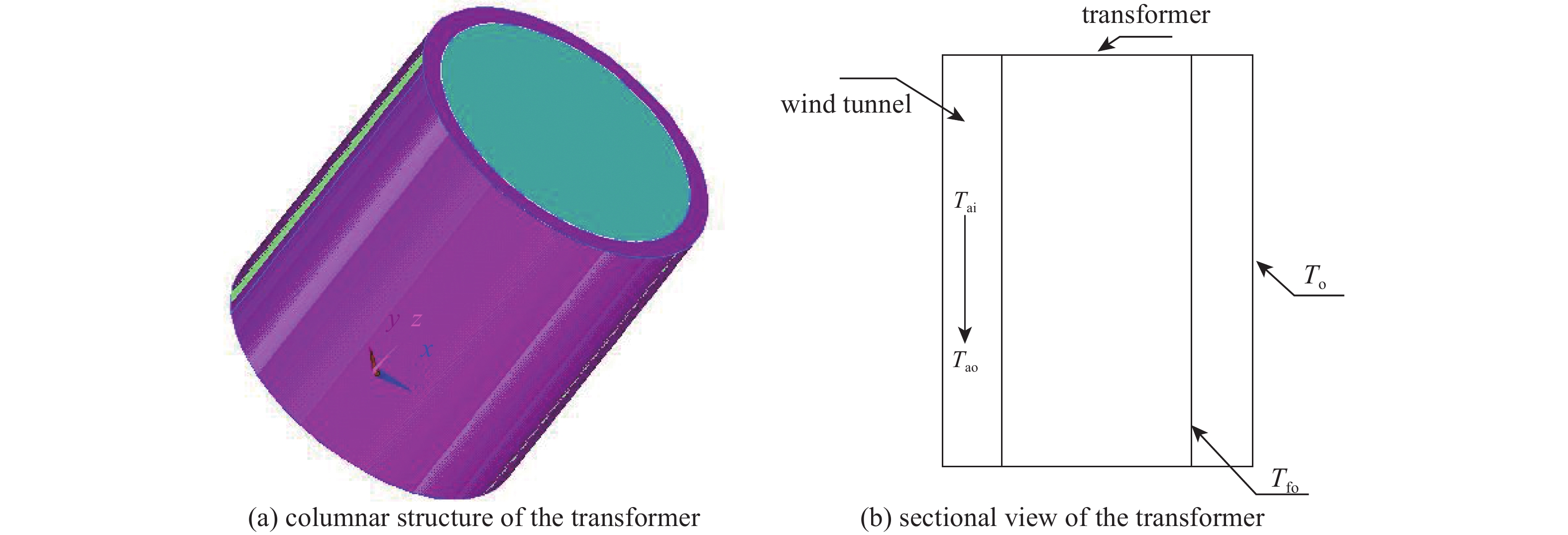
R/m r/m ${P_{{\rm{Cu}}}}$/W ${P_{{\rm{Fe}}}}$/W H/m ${T_{{\rm{fo}}}}$/${}^ \circ {\rm{C}}$ D/m A/m2 0.98 0.74 39 823 10 770 1.8 25 0.20 7.49 表 2 干空气的热物理性质
Table 2. Thermophysical properties of dry air(
$p = 100 \;{\rm{kPa}}$ )$T/{}^\circ {\rm{C}}$ $\;\rho /\left( { {\rm{kg} } \cdot { {\rm{m} }^{\rm{3} } } } \right)$ ${c_p}/\left( {{\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{{\rm{ - 1}}}} \cdot {{\rm{K}}^{{\rm{ - 1}}}}} \right)$ $\;\mu /\left( { {\rm{1} }{ {\rm{0} }^{ {\rm{ - 6} } } }\;{\rm{Pa} } \cdot {\rm{s} } } \right)$ $k/\left( {{\rm{mW}} \cdot {{\rm{m}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}} \right)$ 20 1.164 1.013 18.24 25.24 40 1.092 1.013 19.22 26.52 60 1.025 1.017 20.40 28.03 80 0.968 1.022 20.99 2.931 100 0.916 1.022 21.77 30.70 120 0.870 1.026 22.75 31.98 140 0.827 1.026 23.54 33.26 160 0.789 1.030 24.12 34.42 200 0.732 1.034 25.89 36.98 250 0.653 1.043 27.95 39.77 300 0.596 1.047 29.71 42.91 -
[1] 孙雪静. 超高速永磁同步电机的热设计与大电流检测技术[D]. 西安: 西安电子科技大学, 2012: 43-46.Sun Xuejing. Thermal design and high current detection technology for ultra-high speed permanent magnet synchronous motor. Xi'an: Xidian University, 2012: 43-46 [2] 庞营. 变压器发热与散热的数学研究[J]. 超星, 2014, 1(1):53-54. (Pang Ying. Mathematical study on heating and heat dissipation of transformers[J]. Superstar, 2014, 1(1): 53-54 [3] 张鲁, 李永光, 高向宗, 等. 变压器冷却技术的发展[J]. 能源与节能, 2016, 128(5):109-110. (Zhang Lu, Li Yongguang, Gao Xiangzong, et al. Development of transformer cooling technology[J]. Energy and Energy Conservation, 2016, 128(5): 109-110 doi: 10.3969/j.issn.2095-0802.2016.05.054 [4] 金立军. 变压器室对流换热的分析[J]. 电力建设, 2000(8):19-20. (Jin Lijun. Analysis of convective heat transfer in transformer room[J]. Electric Power Construction, 2000(8): 19-20 doi: 10.3969/j.issn.1000-7229.2000.08.007 [5] 许进峰. ANSYS Workbench 15.0完全自学一本通[M]. 北京: 电子工业出版社, 2014: 426-427.Xu Jinfeng. ANSYS Workbench 15.0 complete self-study guide. Beijing: Publishing House of Electronics Industry, 2014: 426-427 [6] 苏玎, 于学莲. 110 kV级变压器冷却方式的选择[J]. 科技风, 2015(2):11. (Su Ding, Yu Xuelian. Selection of 110 kV transformer cooling method[J]. Science and Technology, 2015(2): 11 doi: 10.3969/j.issn.1671-7341.2015.02.009 [7] 星文彤, 李志尊, 胡仁喜, 等. ANSYS13.0热力学有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2011: 11-16.Xing Wentong, Li Zhizun, Hu Renxi, et al. ANSYS13.0 thermodynamic finite element analysis from entry to proficiency. Beijing: China Machine Press, 2011: 11-16 [8] 郭振华. 大型变压器绕组涡流损耗及热点温度的研究[D]. 河北: 河北工业大学, 2013: 5-8.Guo Zhenhua. Study on eddy current loss and hot spot temperature of large transformer windings. Hebei: Hebei University of Technology, 2013: 5-8 [9] 张锋. 基于ANSYS的DC/DC电源模块热分析和热设计研究[D]. 重庆: 重庆大学, 2008: 27-29.Zhang Feng. Thermal analysis and thermal design of DC/DC power module based on ANSYS. Chongqing: Chongqing University, 2008: 27-29 [10] 邢雅, 樊博, 康亚丽, 等. 树脂绝缘干式变压器内部温度场的计算[J]. 研究与设计, 2016, 40(1):34-38. (Xing Ya, Fan Bo, Kang Yali, et al. Calculation of internal temperature field of resin insulated dry type transformer[J]. Research & Design, 2016, 40(1): 34-38 [11] 谢龙汉. ANSYS FLOTRAN流体与热分析[M]. 北京: 电子工业出版社, 2012: 413-456.Xie Longhan. ANSYS FLOTRAN fluid and thermal analysis. Beijing: Publishing House of Electronics Industry, 2012: 413-456 -




 下载:
下载: