Efficiency of distributed energy storage electromagnetic railgun
-
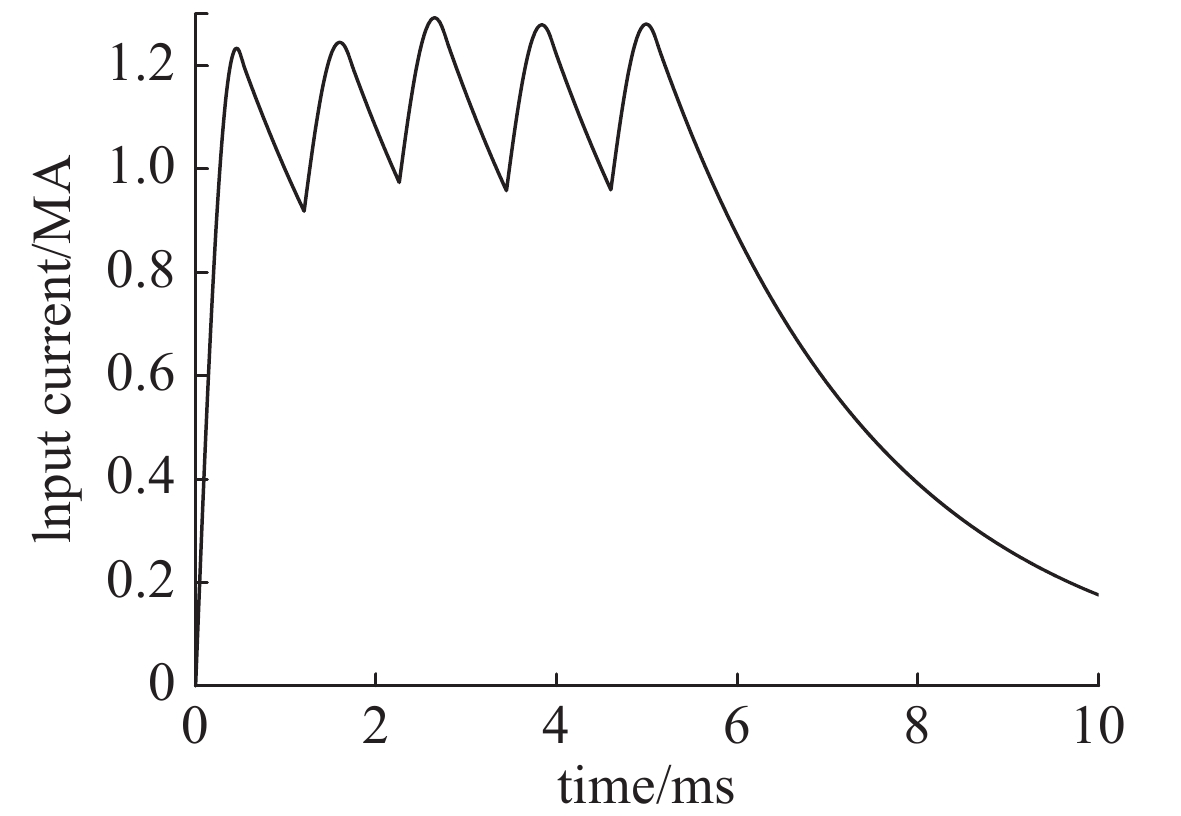
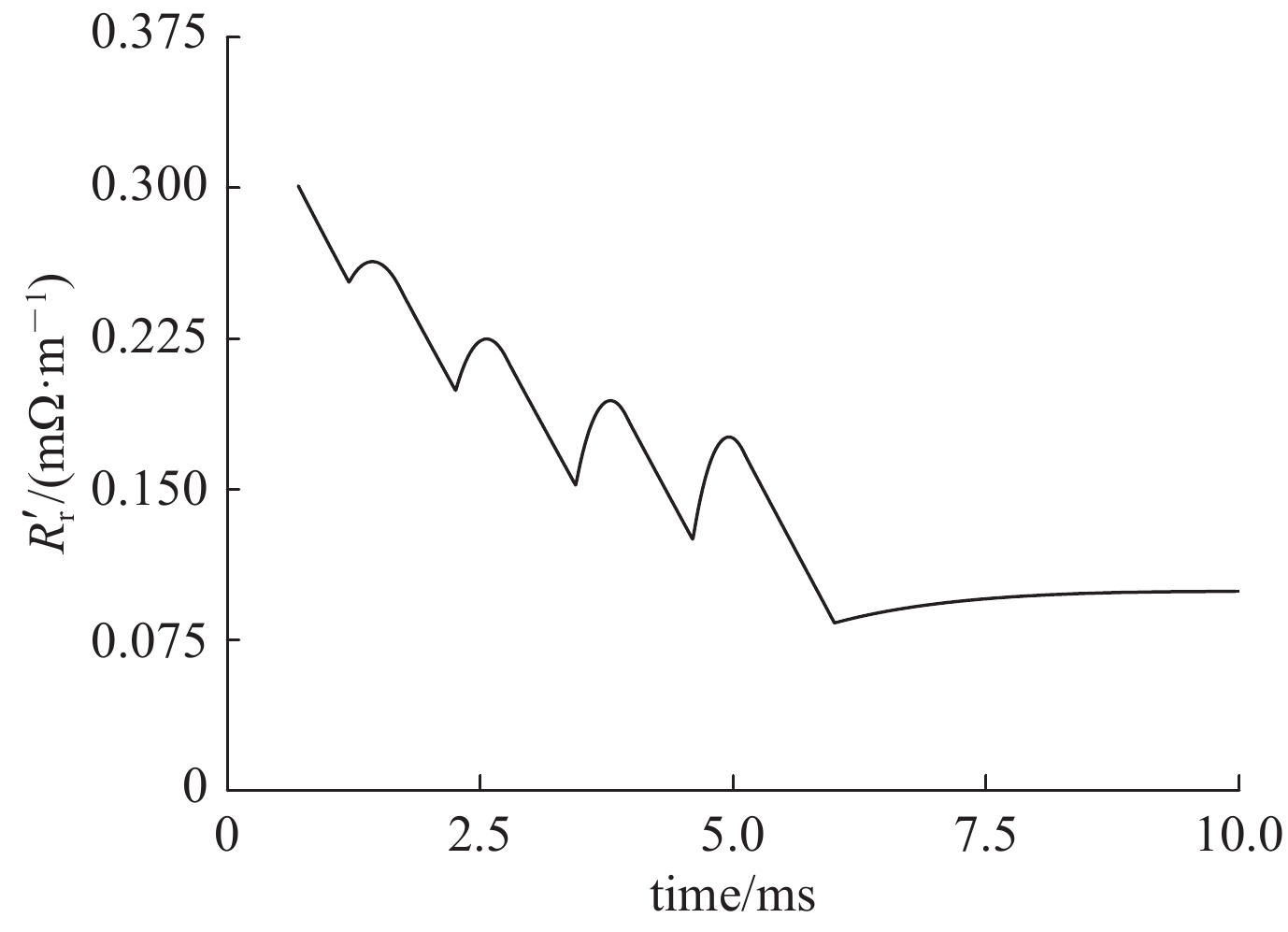
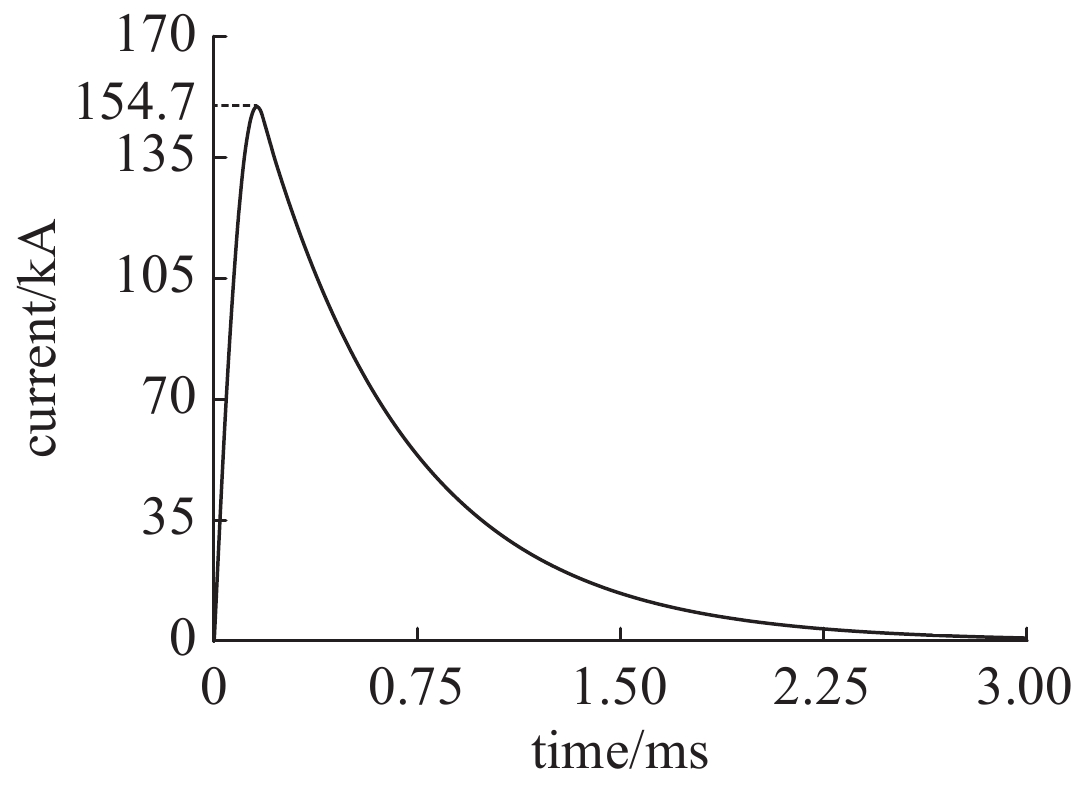
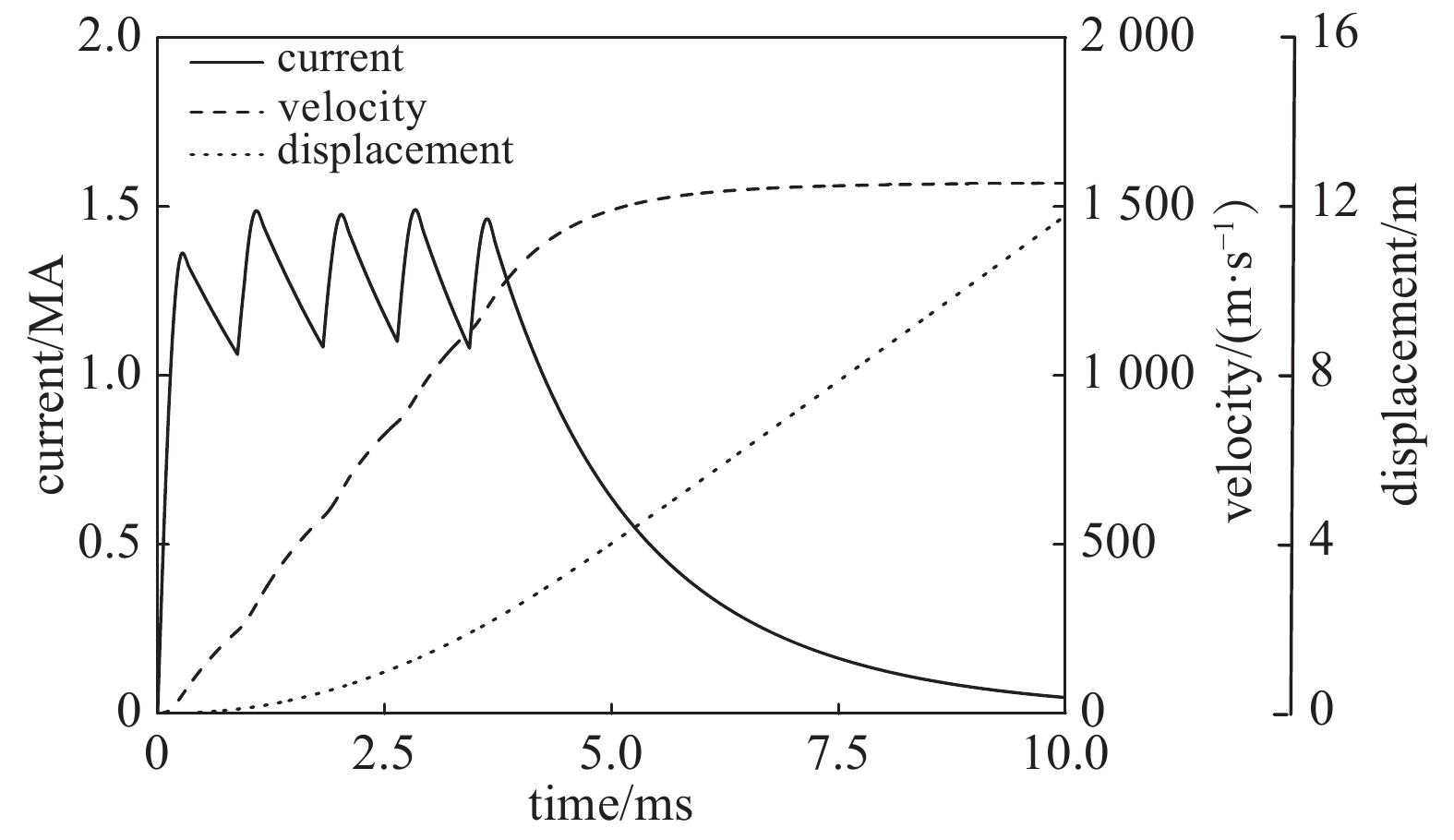
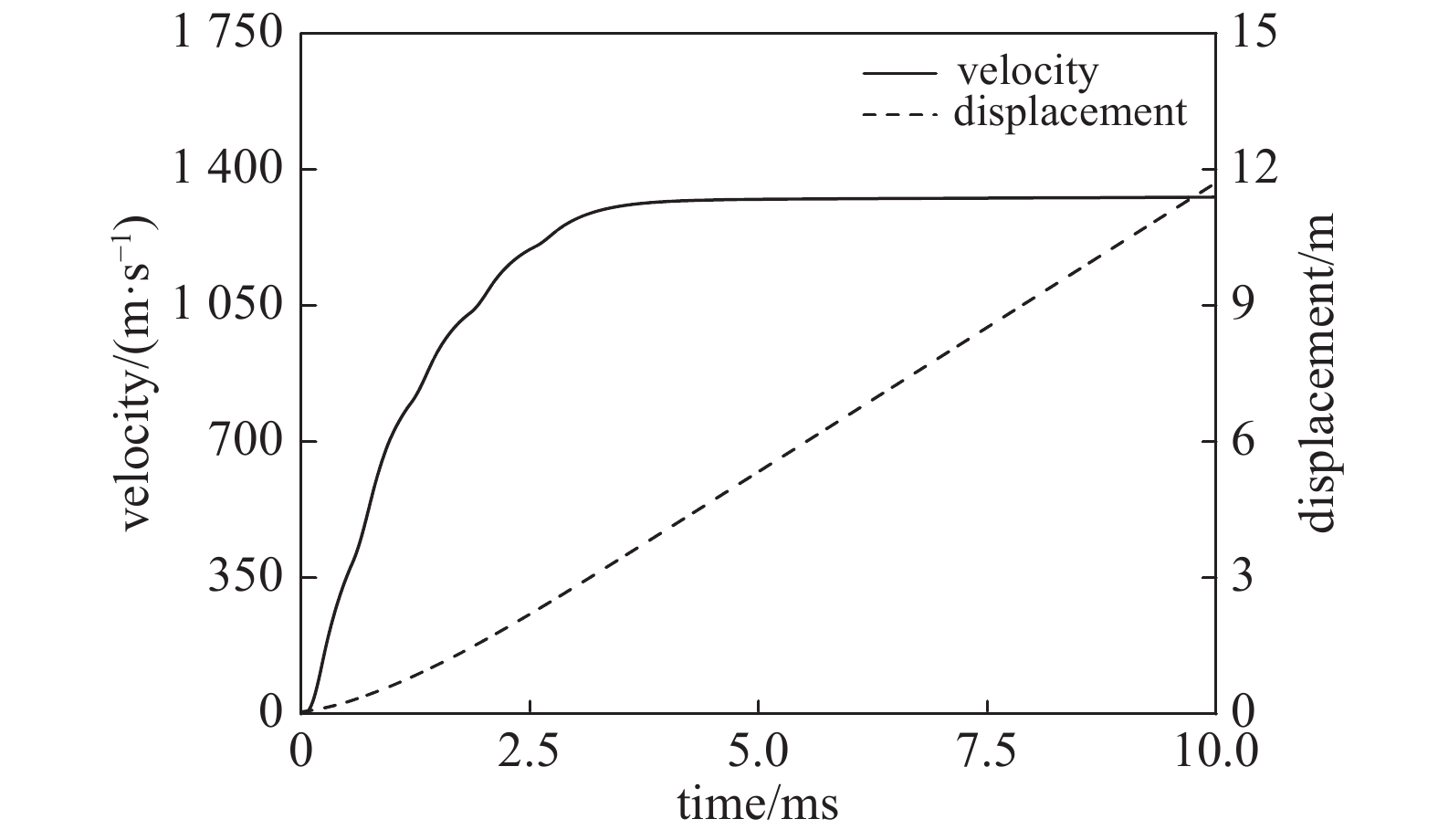
摘要: 分布储能式电磁轨道炮在长导轨发射中具备高发射效率优势,为实现分布储能式电磁轨道炮的恒流特点,建立可供发射器参数、结构设计参考的仿真模型尤为重要。针对口径为60 mm×80 mm的矩形轨道炮,根据电流波形的平稳性要求,沿导轨方向设置电流馈入点,诊断电枢位置并分时序触发各馈入点电源,以测试分布储能式电磁轨道炮的工作性能。在COMSOL三维磁场中建立矩形导轨-电枢模型,基于电流和磁场的多物理场耦合有限元分析得到磁场和电流的分布,并利用电磁场仿真结果实现电流趋肤效应下轨道电阻梯度计算。基于MATLAB SIMULINK平台对电容储能型脉冲功率电源模块建立电气电路;分析分布储能式电磁轨道炮非线性时变的动态特性并建立轨道及电枢阻抗模型,计算正向电磁力、滑动摩擦力构造电枢的运动方程,并使用信号电路建立电枢-导轨模块,通过Simulink测量模块连接两个隔离的网络,仿真计算得到导轨电流及电枢的出膛速度。设计了总储能为4.16 MJ的分布式储能轨道炮,结果显示,电容预充电压为10.8 kV时,导轨长为3 m的分布式电磁轨道炮可将1 kg的弹丸加速至1.4 km/s,与炮尾集中式电磁轨道炮相比,系统发射效率可提升约3%。Abstract: A distributed energy storage (DES) electromagnetic railgun has the advantage of higher efficiency, compared with a breech-fed railgun. A railgun with a caliber of 60 mm×80 mm is designed. In order to stabilize the current waveform, current feed-in points are set along the length of the gun, and the armature position is diagnosed and the pulse power system is triggered by real-time feedback signal to test the performance of the DES railgun. The resistance gradient is calculated by finite element analysis: the coupling field of current field and magnetic field is applied to the rectangular rail-armature model established in the 3D magnetic field of COMSOL. Based on the platform of MATLAB SIMULINK, the power circuit of capacitive energy storage pulse power supply module is established. The impedance models of rail and armature are established according to the non-linear time-varying dynamic characteristics of DES electromagnetic railgun, and the forward electromagnetic force and sliding friction force are calculated to construct the motion equation of armature. The armature-railgun module is built by signal circuit, and the two isolated networks connected through SIMULINK measurement module. The variable step-size ode23tb solver calculate the railgun current and exit velocity. A 4.16 MJ DES electromagnetic railgun is designed. The results show that with 10.8 kV pre-charging voltage of the capacitance, a 3 m long DES electromagnetic railgun can accelerate the 1 kg projectile to 1.4 km/s. Compared with the breech-fed electromagnetic railgun, the launching efficiency of the system can be increased by about 3%.
-
Key words:
- distributed energy storage /
- railgun /
- efficiency /
- resistance gradient
-
表 1 电磁轨道炮的系统参数
Table 1. Parameters of electromagnetic railgun
Lri′/(μH·m) ρr/(m·Ω) Rri′/μΩ uc u2 ma+p/kg ρa/(m·Ω) k1 βa/(m2·Ω·A-1) u1 rail armature-projectile system 0.45 1.67×10-8 7.9 0.34 0.32 1 1.67×10-8 2.5×10-2 3×10-16 0.68 表 2 触发单元铺设方式
Table 2. PFU laying mode
trigger sequence x/m total units 1 0 14 2 0.1 8 3 0.2 7 4 1.1 6 5 1.9 5 -
[1] Marshall, R A. Distributed energy store railgun: the limiting case[J]. IEEE Trans Magnetics, 1991, 27(1): 136-138. doi: 10.1109/20.101009 [2] Matyac M J, Christopher F, Jamison K A, et al. Railgun performance enhancement from distribution of energy feeds[J]. IEEE Trans Magnetics, 1995, 31(1): 332-337. doi: 10.1109/20.364666 [3] Hundertmark S, Simicic D, Vincent G. Acceleration of aluminum booster projectiles with PEGASUS[J]. IEEE Trans Plasma Science, 2015, 43(5): 1147-1151. doi: 10.1109/TPS.2015.2401054 [4] Lehmann P, Peter H, Wey J. First experimental results with the ISL 10 MJ DES railgun PEGASUS[J]. IEEE Trans Magnetics, 2001, 37(1): 435-439. doi: 10.1109/20.911871 [5] 贾义政. 圆膛四轨电磁轨道炮的动力学建模与仿真[D]. 南京: 南京理工大学, 2015.Jia Yizheng. Dynamics modeling and simulation of four foure round rails electromagnetic railgun. Nanjing: Nanjing University of Science and Technology, 2015 [6] 关永超, 邹文康, 何勇, 等. 串联型双轨增强电磁轨道炮电路模拟[J]. 强激光与粒子束, 2014, 26(11):226-230. (Guan Yongchao, Zou Wenkang, He Yong, et al. Circuit simulation of the electromagnetic railgun system[J]. High Power Laser and Particle Beams, 2014, 26(11): 226-230 [7] Zhou Yuan, Yan Ping, Sun Yaohong, et al. Design of a distributed-energy-store railgun[J]. IEEE Trans Plasma Science, 2011, 39(1): 230-234. doi: 10.1109/TPS.2010.2049032 [8] Zhou Yuan, Yan Ping, Sun Yaohong, et al. Analysis on efficiency improvement with a distributed energy store railgun[C]//IEEE International Power Modulator and High Voltage Conference. 2010. [9] Deadrick F, Hawke R, Scudder J. MAGRAC—A railgun simulation program[J]. IEEE Trans Magnetics, 2003, 18(1): 94-104. [10] Smith A N, Ellis R L, Bernardes J S, et al. Thermal management and resistive rail heating of a large-scale naval electromagnetic launcher[C]//IEEE 12th Symposium on Electromagnetic Launch Technology. 2005. [11] Weeks D A, Weldon W F, Zowarka R C. Plasma armature railgun launcher simulations at the University of Texas at austin[J]. IEEE Trans Magnetics, 1989, 25(1): 580-586. doi: 10.1109/20.22604 [12] Aigner S, Igenbergs E. Friction and ablation measurements in a round bore railgun[J]. IEEE Trans on Magnetics, 1989, 25(1): 33-39. doi: 10.1109/20.22500 -




 下载:
下载: