Two-phase streamer characteristics in transformer oil under nanosecond impulses voltages
-
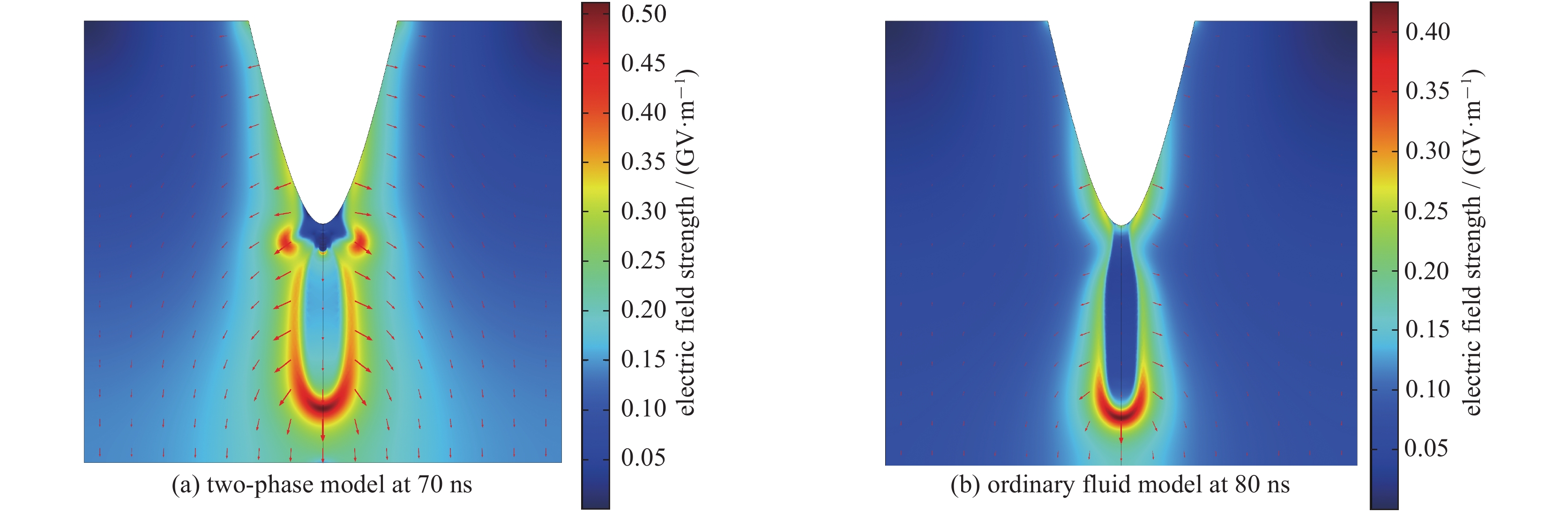
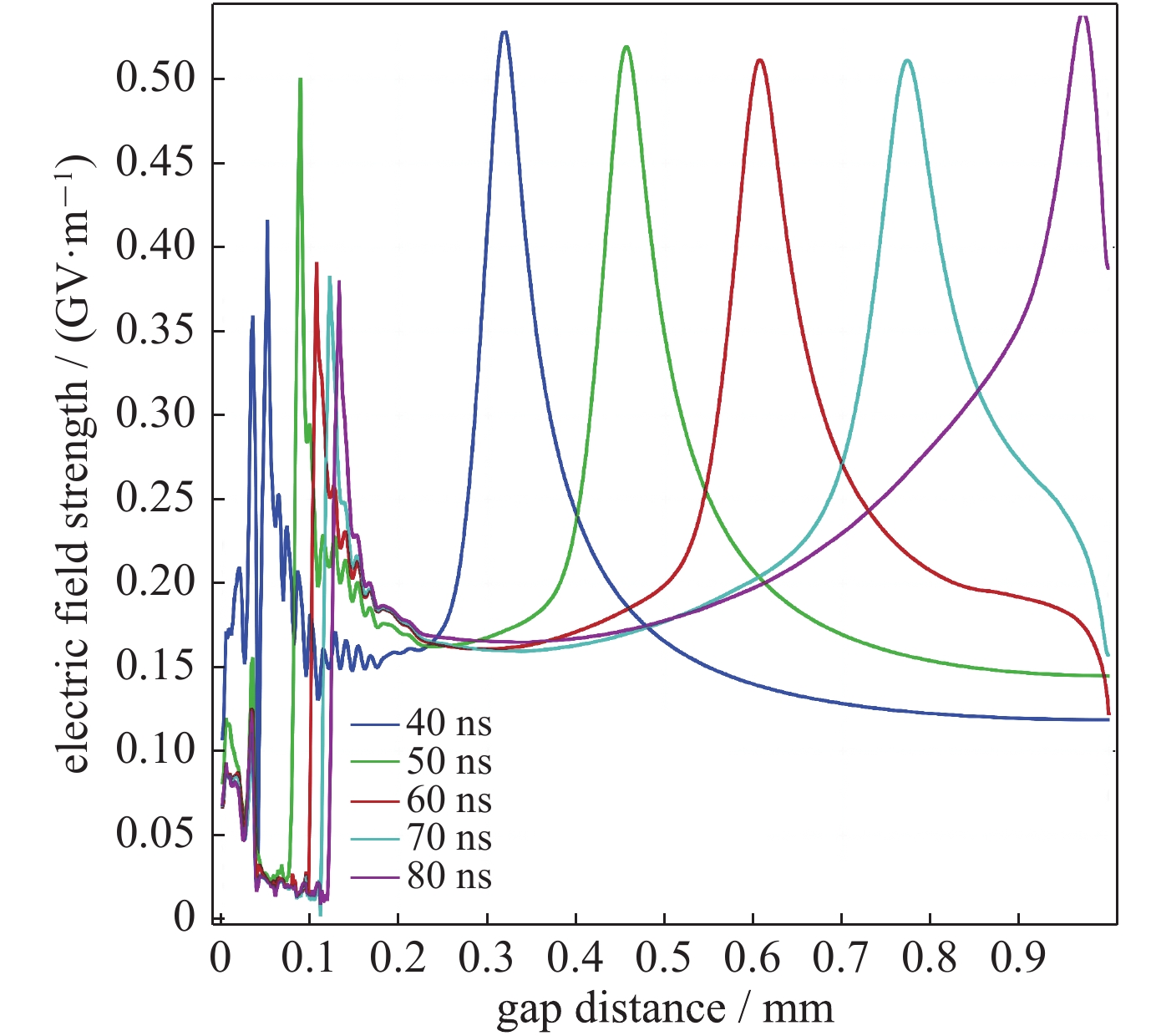
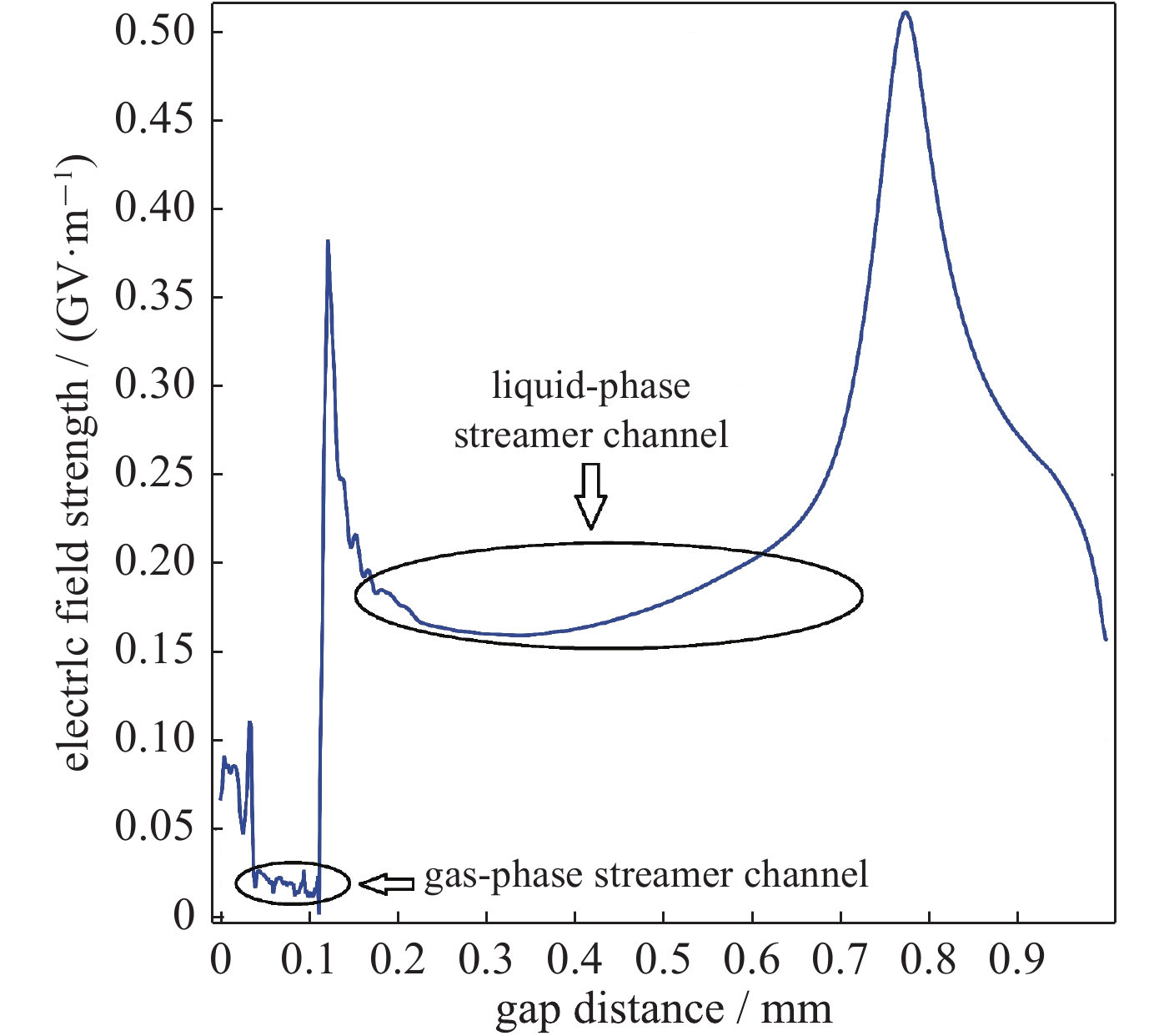
摘要: 为揭示液体电介质击穿过程中形成的气体放电通道对液体电介质放电过程的影响,以针—板电极间隙变压器油为研究对象,基于等离子体流体力学模型,引入了液体电介质放电过程中气相放电通道对电离机制及自由电荷迁移率的影响,建立了用于模拟脉冲电压下液体电介质放电过程的两相流体模型,仿真研究了纳秒脉冲下针板电极流注放电的起始与发展过程。仿真结果表明:采用Heaviside方程可以在模型的不同区域同时实现气相物理过程和液相物理过程的模拟与计算。气相物理过程的引入导致流注尾部电场显著降低,流注头部电场进一步增强,使流注通道的发展速度要高于传统液相模型,有助于加深对纳秒脉冲下液体电介质中预击穿流注的起始、发展过程的认识和理解。Abstract: To reveal the influence of the formation and development of gas-phase streamer channel on liquid discharge between pin-plane electrodes, a numerical model of the transformer-oil discharge in the pin-plane electrode system is built based on the continuity equations of free charge carriers, which are coupled with the Poisson’s equation. The gas-phase processes during the streamer development process is also taken into consideration, including impact ionization and the increase in the mobility of free charge carriers in the gas-phase relative to the liquid-phase in the streamer channel. The Heaviside function is used to switch the simulation model between gas-phase and liquid-phase. The initial and propagation progress of streamer discharge under nano-second pulse voltage is simulated using the model. Simulating results show that the electric field at the streamer body is significantly reduced and the electric field at the head of the streamer is further enhanced with the addition of such low density gas-phase region. The propagation speed of the streamer in two-phase model is also faster than that of the ordinary liquid-phase model.
-
Key words:
- nanosecond impulse /
- transformer oil /
- streamer /
- space charge density /
- liquid-gas phase
-
表 1 液相流注仿真所需主要物理参数
Table 1. Physical parameters required for simulation of liquid phase
μpLP/(m2·V−1·s−1) μnLP/(m2·V−1·s−1) μeLP/(m2·V−1·s−1) Rpe/(m3·s−1) Rpn/(m3·s−1) n0/m−3 a/m τa/s Δ/eV 1×10−9 1×10−9 1×10−4 1.64×10−17 1.64×10−17 1×1023 3×10−10 2×10−7 7.5 表 2 变压器油传热参数
Table 2. Thermal parameters of transformer oil
ρl/(kg·m−3) cv/(J·kg−1·K−1) kT/(W·m−1·K−1) 880 1.7×103 0.13 表 3 气相流注通道仿真所需主要物理参数
Table 3. physical parameters required for simulation of gas phase
μeGP/(m2·V−1·s−1) α0/m−1 β0/(V·m−1) μpGP/(m2·V−1·s−1) μnGP/(m2·V−1·s−1) 1×10−2 25 2×107 1×10−7 1×10−7 -
[1] Lesaint O. Prebreakdown phenomena in liquids: propagation ‘modes’ and basic physical properties[J]. Journal of Physics D: Applied Physics, 2016, 49(14): 144001. doi: 10.1088/0022-3727/49/14/144001 [2] Bluhm H. Pulsed power systems[M]. Karlsruhe: Springer, 2006. [3] 张晋琪, 蒋兴良, 陈志刚. 液体介质快脉冲电压下击穿特性研究[J]. 强激光与粒子束, 2006, 18(6):1053-1056. (Zhang Jinqi, Jiang Xingliang, Chen Zhigang. Characteristics study of short-pulsed dielectric breakdown in liquids[J]. High Power Laser and Particle Beams, 2006, 18(6): 1053-1056 [4] 黄文力, 孙广生, 王珏, 等. 液体介质击穿机理研究进展[J]. 高压电器, 2005(2):131-134. (Huang Wenli, Sun Guangsheng, Wang Jue, et al. Progress in the study of breakdown mechanism about liquid dielectric[J]. High Voltage Apparatus, 2005(2): 131-134 doi: 10.3969/j.issn.1001-1609.2005.02.017 [5] 王珏, 邵涛, 袁伟群, 等. 重频纳秒高压脉冲下变压器油击穿特性的实验研究[J]. 强激光与粒子束, 2005, 17(2):268-270. (Wang Jue, Shao Tao, Yuan Weiqun, et al. Study on transformer oil breakdown under repetitive nanosecond pulses[J]. High Power Laser and Particle Beams, 2005, 17(2): 268-270 [6] 章程, 邵涛, 牛铮, 等. 大气压尖板电极结构重复频率纳秒脉冲放电中X射线辐射特性研究[J]. 物理学报, 2012, 61(3):305-313. (Zhang Cheng, Shao Tao, Niu Zheng, et al. X-ray generation in repetitive pulsed discharge in atmospheric air with a point-to-plane gap[J]. Acta Physica Sinica, 2012, 61(3): 305-313 [7] Hwang G. Elucidating the mechanisms behind pre-breakdown phenomena in transformer oil systems[D]. Cambridge: Massachusetts Institute of Technology, 2010. [8] 李元, 穆海宝, 邓军波, 等. 正极性纳秒脉冲电压下变压器油中流注放电仿真研究[J]. 物理学报, 2013, 62(12):334-344. (Li Yuan, Mu Haibao, Deng Junbo, et al. Simulation study on streamer discharge in transformer oil under positive nanosecond pulse voltage[J]. Acta Physica Sinica, 2013, 62(12): 334-344 [9] 施健, 司马文霞, 杨庆, 等. 初始条件对变压器油中流注特性的影响[C]//重庆市电机工程学会学术会议. 2012: 877-882.Shi Jian, Sima Wenxia, Yang Qing, et al. Influence of initial condition on the propagation of streamer in transformer oil//Conference of Chong Qing Society of Electrical Engineering. 2012: 877-882 [10] IEC Standard #60897 (1987) Methods for the determination of lightning impulse breakdown voltage of insulating liquid[S]. [11] Jadidian J, Hwang G, Zahn M, et al. Migration-ohmic charge transport in liquid-solid insulation systems[C]//IEEE International Conference on Dielectric Liquids. 2011: 1. [12] Jadidian J, Hwang G. Streamer initiation and propagation in transformer oil under positive and negative impulse voltages[C]//Pulsed Power Conference. 2011: 251 [13] Jadidian J, Zahn M. Charge transport analysis in two-phase composite dielectric systems[J]. IEEE Trans Plasma Science, 2013, 41(9): 2464-2474. doi: 10.1109/TPS.2013.2276420 [14] Meek F, Craggs J. Electrical breakdown of gases[M]. New York: John Wiley & Sons, 1978. [15] 王同磊, 张乔根, 倪鹤立, 等. 变压器油中阴极放电起始过程的气泡模型[J]. 高电压技术, 2017, 43(6):2042-2048. (Wang Tonglei, Zhang Qiaogen, Ni Heli, et al. Bubble model of breakdown initiation process from cathode in transformer oil[J]. High Voltage Engineering, 2017, 43(6): 2042-2048 -




 下载:
下载: