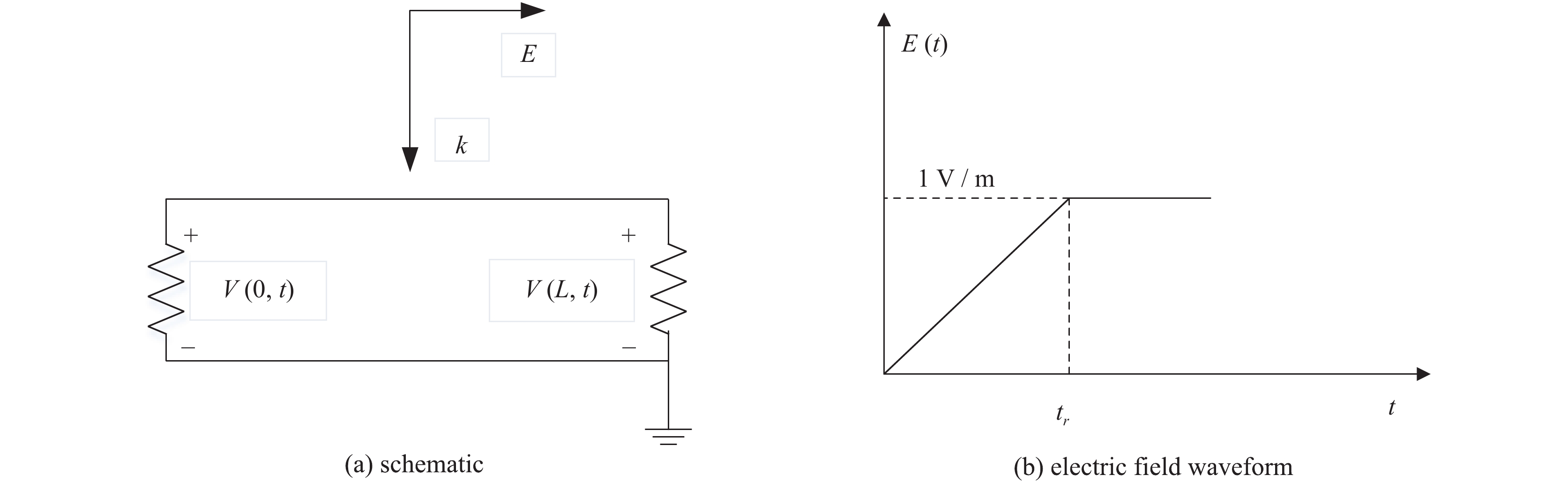
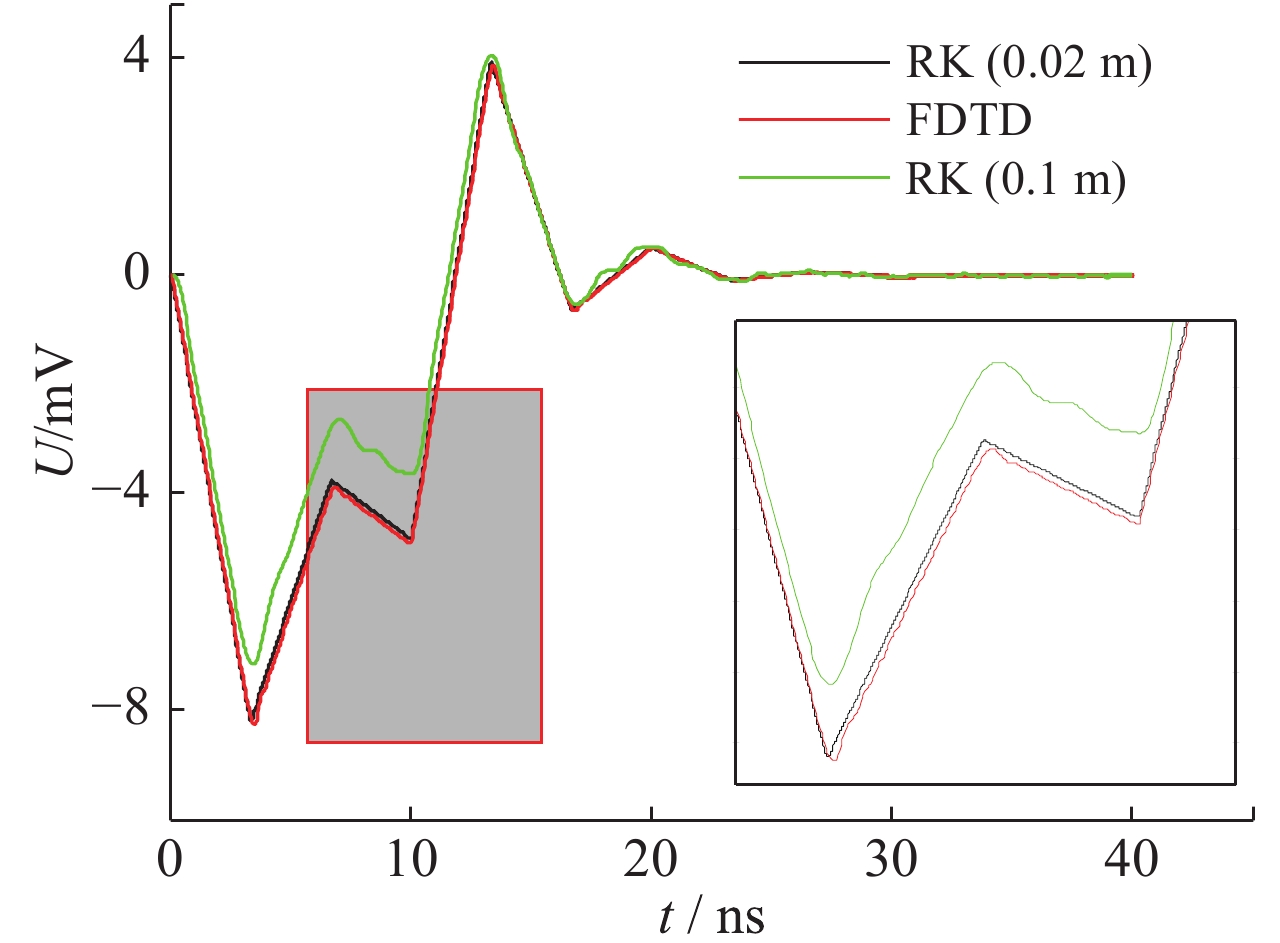
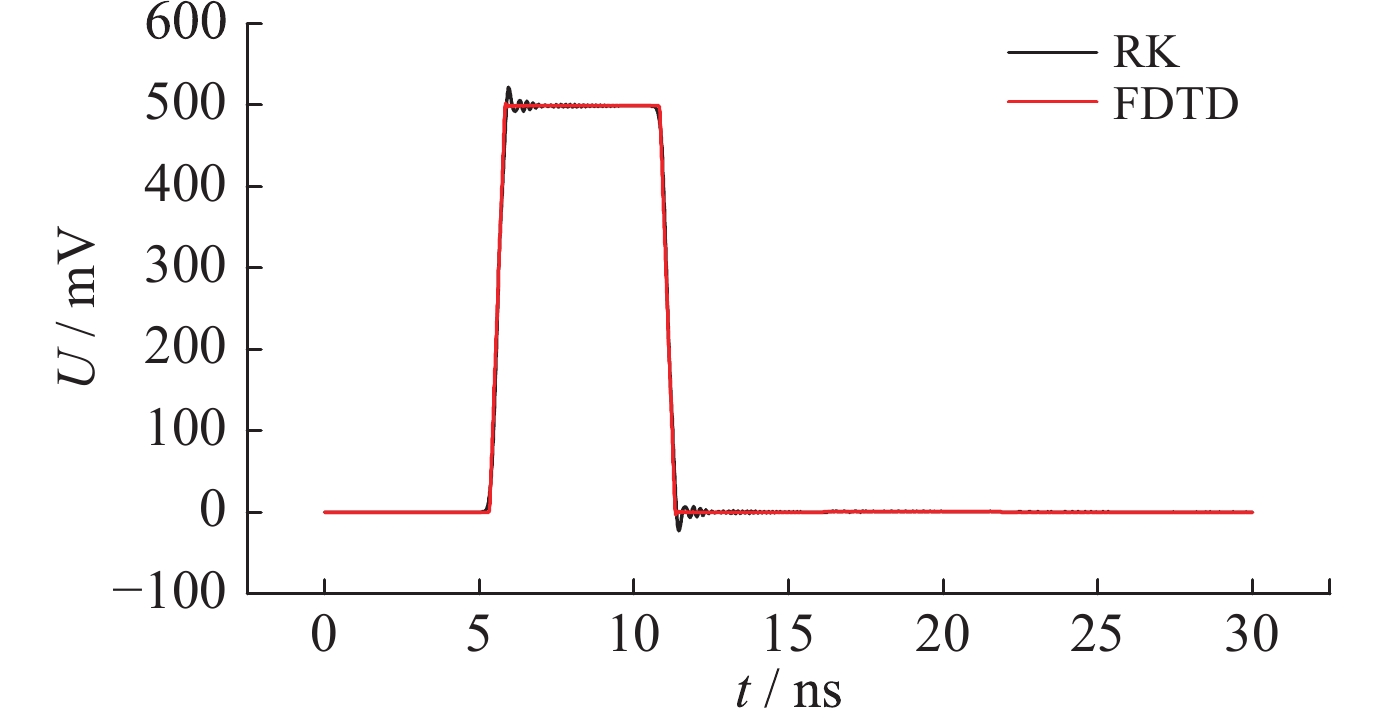
| [1] |
张希. 有损均匀传输线数值解的研究[D]. 重庆: 重庆大学, 2003: 42-59.Zhang Xi. Reasearch on lossy and uniform transmission line numerical solution[D]. Chongqing: Chongqing University, 2000: 21-30
|
| [2] |
张希, 刘宗行, 孙韬, 等. 传输线方程的一种数值解法[J]. 重庆大学学报(自然科学版), 2004, 27(2):116-119. (Zhang Xi, Liu Zongxing, Sun Tao, et al. A numerical method for transmission line equations[J]. Journal of Chongqing University(Natural Science Edition), 2004, 27(2): 116-119
|
| [3] |
杨阳. 龙格库塔法求模糊微分方程的数值解[D]. 哈尔滨: 哈尔滨工业大学, 2015: 25-35.Yang Yang. Numerical solution of fuzzy differential equations by Runge-Kutta method[D]. Harbin: Harbin Institute of Technology, 2015: 25-35
|
| [4] |
秦浩东, 吴志强, 张晏铭, 等. 龙格-库塔方法与差分法的比较[J]. 成都大学学报(自然科学版), 2014, 33(4):337-338. (Qin Haodong, Wu Zhiqiang, Zhang Yanming, et al. Comparison of Runge-Kutta method and difference method[J]. Journal of Chengdu University(Natural Science Edition), 2014, 33(4): 337-338
|
| [5] |
陈山. 求解波动方程的龙格-库塔型方法及其地震波传播模拟[D]. 北京: 清华大学, 2010: 8-10.Chen shan. The Runge-Kutta type method for solving wave equations and its simulation of seismic wave propagation[D]. Beijing: Tsinghua University, 2010: 8-10
|
| [6] |
梁华力, 富明慧. 一种改进的精细-龙格库塔法[J]. 中山大学学报(自然科学版), 2009, 48(5):2-5. (Liang Huali, Fu Minghui. An improved precise Runge-Kutta integration[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2009, 48(5): 2-5
|
| [7] |
关冶, 陆金甫. 数值分析基础[M]. 北京: 高等教育出版社, 2010.Guan Ye, Lu Jinpu. Fundamentals of numerical analysis[M]. Beijing: Higher Education Press, 2010
|
| [8] |
Paul C R. 多导体传输线分析[M]. 3版. 北京: 中国电力出版社, 2013.Paul C R. Analysis of multiconductor transmission lines[M]. 3rd ed. Beijing: China Electric Power Press, 2013
|
| [9] |
葛德彪, 闫玉波. 电磁波时域有限差分法[M]. 3版. 西安: 西安电子科技大学出版社, 2011.Ge Debiao, Yan Yubo. Finite-difference time-domain method for electromagnetic waves[M]. 3rd ed. Xi′an: Xidian University Press, 2011
|
| [10] |
冀维林. 基于FDTD算法的多导体传输线电磁兼容的研究[D]. 北京: 北京邮电大学, 2010: 21-43.Ji Weilin. Study on electromagnetic compatibility of transmission line based on FDTD method[D]. Beijing: Beijing University of Posts and Telecommunications, 2010: 21-43
|





 下载:
下载: