Numerical simulation and experimental verification on distribution characteristics of hydrogen flow in single compartment
-
摘要:
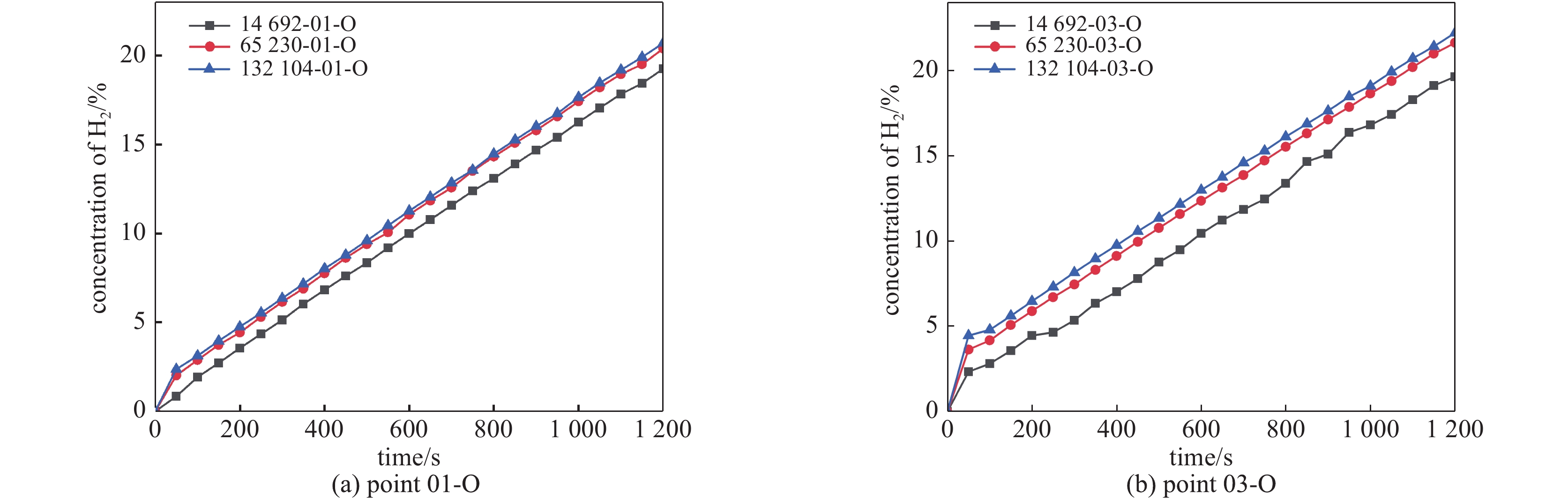
以局部隔间氢气流动分布特性研究实验装置中的单个隔间作为几何结构,建立小空间内氢气分布数值研究的计算流体动力学分析模型,对不同湍流模型适用性展开讨论分析,通过对比实验数据和模拟数据,给出最优湍流模型的选择,进一步对低质量流量工况下氢气在小空间内的流动分布进行数值模拟。模拟结果表明:在选取的6种两方程湍流模型中,采用Realizable k-ε、RNG k-ε、Standard k-ε湍流模型计算得到的结果与实验值吻合较好,能够准确地反映氢气在小空间内的释放过程和分布情况;低质量流量工况下,氢气主流区域径向范围较小,氢气在容器中上部呈稳定均匀分布。
Abstract:The distribution characteristics of hydrogen flow in local single space is a special concern of nuclear power plant and hydrogen storage device. In this paper, a single compartment of the experimental device is used as a geometric structure to establish a computational fluid dynamics analysis model for the numerical study of hydrogen distribution in small-scale space. By comparing the experimental data with the simulated data, the choice of the optimal turbulence model is given, and the flow distribution of hydrogen in small-scale space under low mass flow rate condition is simulated. The numerical simulation results obtained by Realizable k-ε, RNG k-ε and Standard k-ε turbulence models in the six two-equation turbulence models agree well with the experimental data, which can accurately reflect the release process and distribution of hydrogen in small-scale space. In low mass flow rate case, the radial range of the mainstream region of hydrogen is small, and hydrogen is stably and evenly distributed in the middle and upper part of the compartment.
-
Key words:
- single compartment /
- hydrogen /
- turbulence model /
- numerical simulation /
- flow distribution
-
表 1 三种网格划分参数
Table 1. Meshing parameters of three kinds of grids
grid nodes cells maximum skewness coarse grid 78 997 14 692 0.401 middle grid 264 642 65 230 0.414 fine grid 522 207 132 104 0.413 -
[1] Dimmelmeier H, Jürgen E, Movahed M A. Computational validation of the EPR combustible gas control system[J]. Nuclear Engineering and Design, 2012, 249: 118-124. doi: 10.1016/j.nucengdes.2011.08.053 [2] Deng Jian, Cao Xuewu. A study on implementing a passive autocatalytic recombiner PAR-system in the large-dry containment[J]. Nuclear Engineering and Design, 2008, 238(7): 2554-2560. [3] Prasad K, Pitts W M, Yang J C. A numerical study of the release and dispersion of a buoyant gas in partially confined spaces[J]. International Journal of Hydrogen Energy, 2011, 36(8): 5200-5210. doi: 10.1016/j.ijhydene.2011.01.118 [4] Cariteau B, Brinster J, Tkatschenko I. Experiments on the distribution of concentration due to buoyant gas low flow rate release in an enclosure[J]. International Journal of Hydrogen Energy, 2011, 36(3): 2505-2512. doi: 10.1016/j.ijhydene.2010.04.054 [5] Cariteau B, Tkatschenko I. Experimental study of the effects of vent geometry on the dispersion of a buoyant gas in a small enclosure[J]. International Journal of Hydrogen Energy, 2013, 38(19): 8030-8038. doi: 10.1016/j.ijhydene.2013.03.100 [6] Xiao Jianjun, Travis J R. How critical is turbulence modeling in gas distribution simulations of large-scale complex nuclear reactor containment?[J]. Annals of Nuclear Energy, 2013, 56: 227-242. doi: 10.1016/j.anucene.2013.01.016 [7] Müller C, Hughes E D, Niederauer G F, et al. GASFLOW: A computational fluid dynamics code for gases, aerosols, and combustion, volume 3: Assessment manual[J]. Office of Scientific & Technical Information Technical Reports, 1998. [8] Wilkening H, Baraldi D, Heitsch M. CFD simulations of light gas release and mixing in the Battelle Model-Containment with CFX[J]. Nuclear Engineering and Design, 2008, 238(3): 618-626. doi: 10.1016/j.nucengdes.2007.02.042 [9] Peng Cheng, Tong Lili, Cao Xuewu. Numerical analysis on hydrogen stratification and post-inerting of hydrogen risk[J]. Annals of Nuclear Energy, 2016, 94: 451-460. doi: 10.1016/j.anucene.2016.04.029 [10] Swain M R, Shriber J, Swain M N. Comparison of hydrogen, natural gas, liquified petroleum gas, and gasoline leakage in a residential garage[J]. Energy & fuels, 1998, 12(1): 83-89. [11] Agranat V, Cheng Z, Tchouvelev A. CFD modeling of hydrogen releases and dispersion in hydrogen energy station[C]//Proceedings of the 15th World Hydrogen Energy Conference. 2004. [12] Sonnenkalb M, Poss G. The international test programme in the THAI facility and its use for code validation[C]//EUROSAFWE Forum. 2009. [13] Schefer R W, Houf W G, Williams T C. Investigation of small-scale unintended releases of hydrogen: Buoyancy effects[J]. International Journal of Hydrogen Energy, 2008, 33(17): 4702-4712. doi: 10.1016/j.ijhydene.2008.05.091 [14] Houf W, Schefer R. Analytical and experimental investigation of small-scale unintended releases of hydrogen[J]. International Journal of Hydrogen Energy, 2008, 33(4): 1435-1444. doi: 10.1016/j.ijhydene.2007.11.031 -




 下载:
下载: