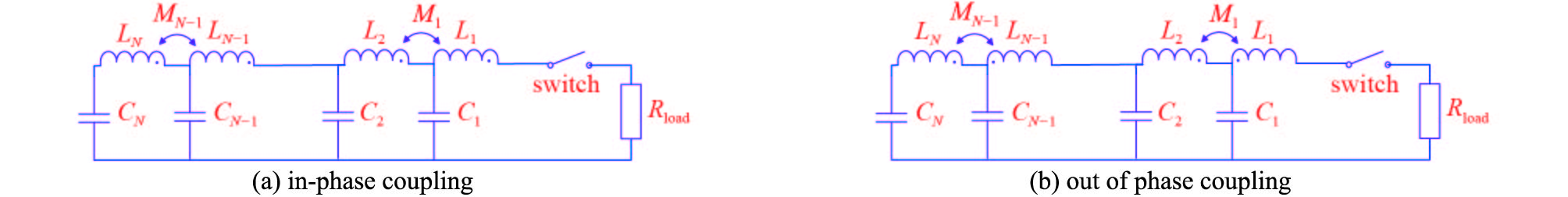Design of square pulse forming network with adjacent mutual coupling inductors
-
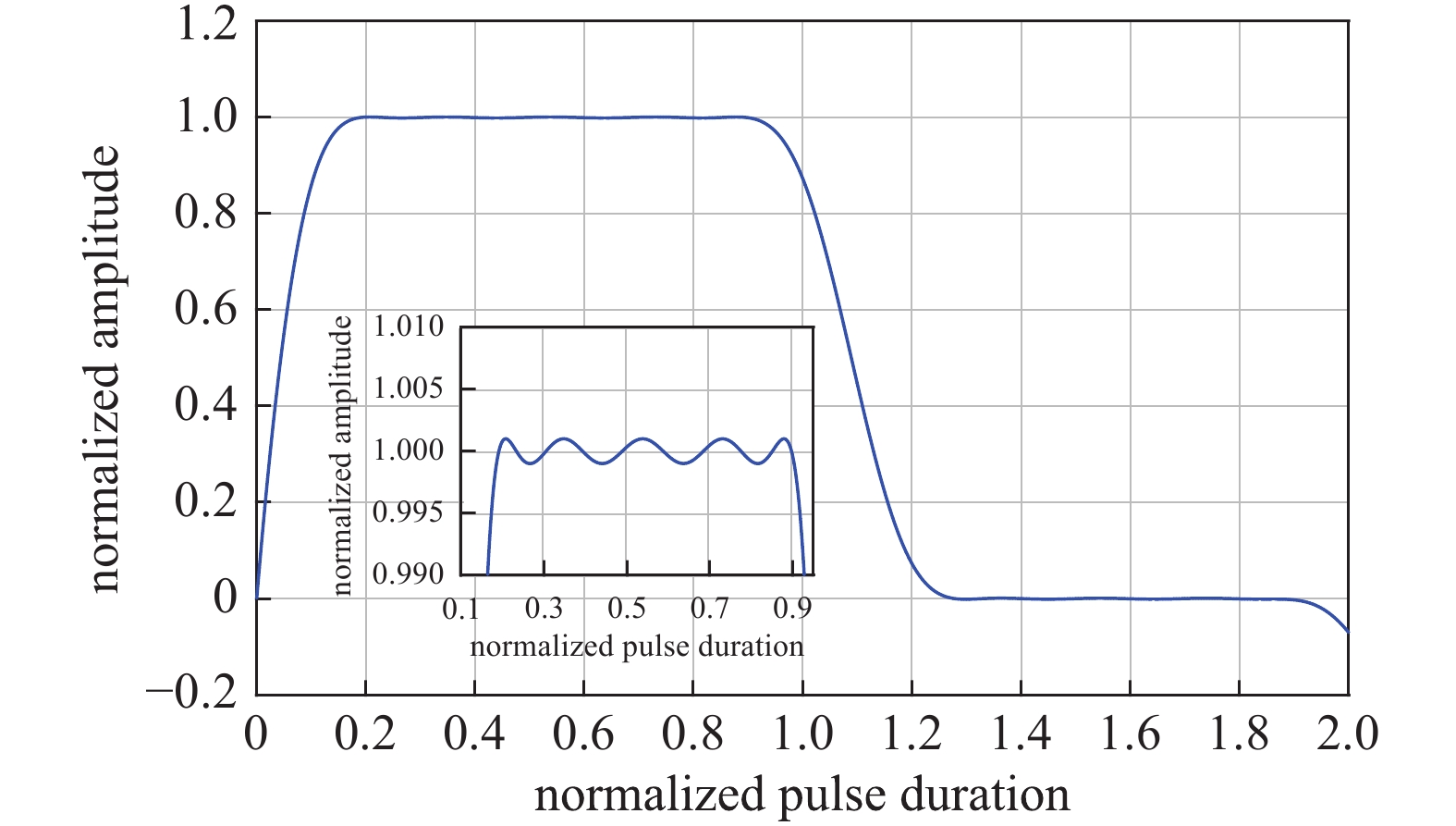
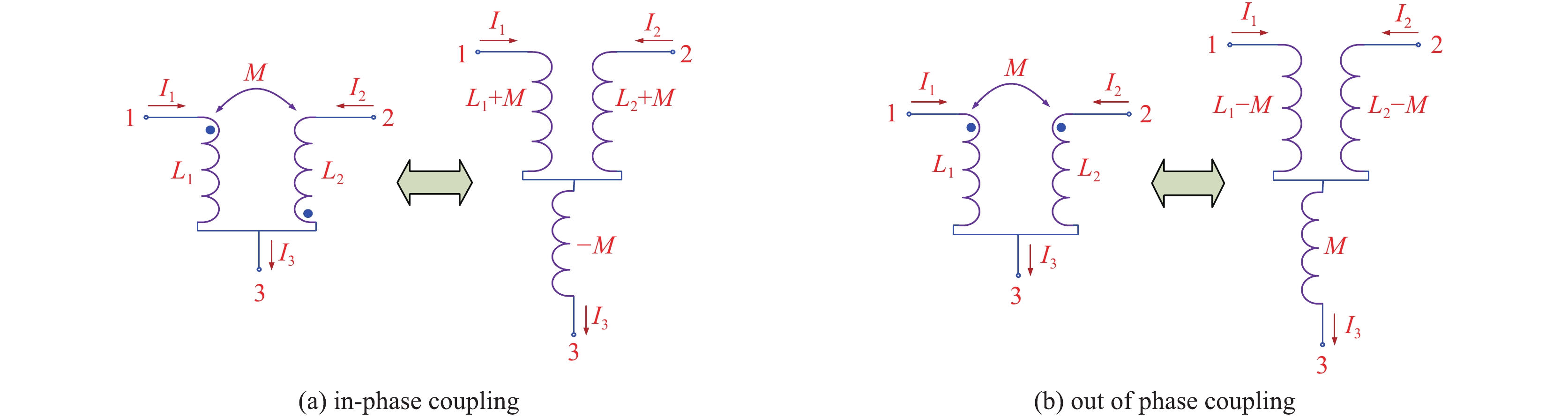
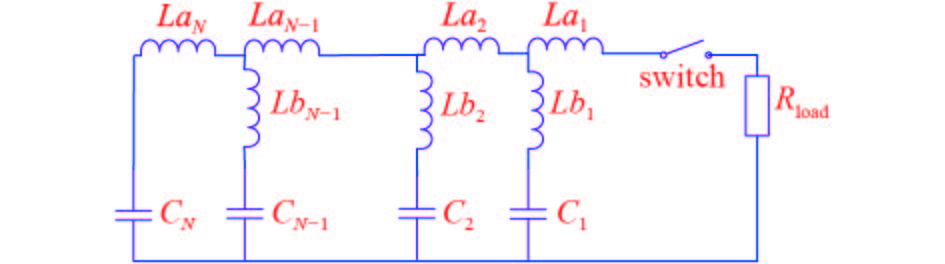
摘要: 针对小型化紧凑型脉冲源的应用需求,开展了电感存在互耦的准方波脉冲形成网络设计技术研究。首先介绍了基于坐标轮换-直接搜索法的准方波脉冲形成网络优化技术研究,获得了网络元件的电感、电容值以及准方波的解析表达式;然后推导了邻近电感互耦网络的等效去耦电路解算方法,基于回溯法,最终给出了全网络各元件值的求解算法;最后分别针对等电容情形及规定电容的情形,求解给出了网络元件参数值。算例结果表明:电感存在互耦的准方波脉冲形成网络可获得较理想的准方波脉冲输出。基于互耦电感的巧妙设计,有利于实现紧凑型准方波脉冲形成网络的设计。Abstract: Considering the application requirement of compact and miniaturized pulse source, the design technique of the quasi-square wave pulse forming network with adjacent mutual coupling inductors is studied. Firstly, the network optimization technique based on the univariate search method is introduced, and the values of the inductance and capacitance and the analytical expressions of quasi-square wave are obtained. Then the equivalent decoupling circuit of the network with adjacent mutual coupling inductors is deduced. Based on the backtracking algorithm, the method for calculating the values of each element in the network is given. Finally, in cases of equal capacitance and constrained capacitance, the parameters of each element in the network are given. The numerical results show that the ideal quasi-square-wave pulse with a certain width flat-top can be produced by using the designed PFN with adjacent mutual coupling inductors. The ingenious design based on mutual coupling inductance is beneficial to the design of compact quasi-square wave pulse forming network.
-
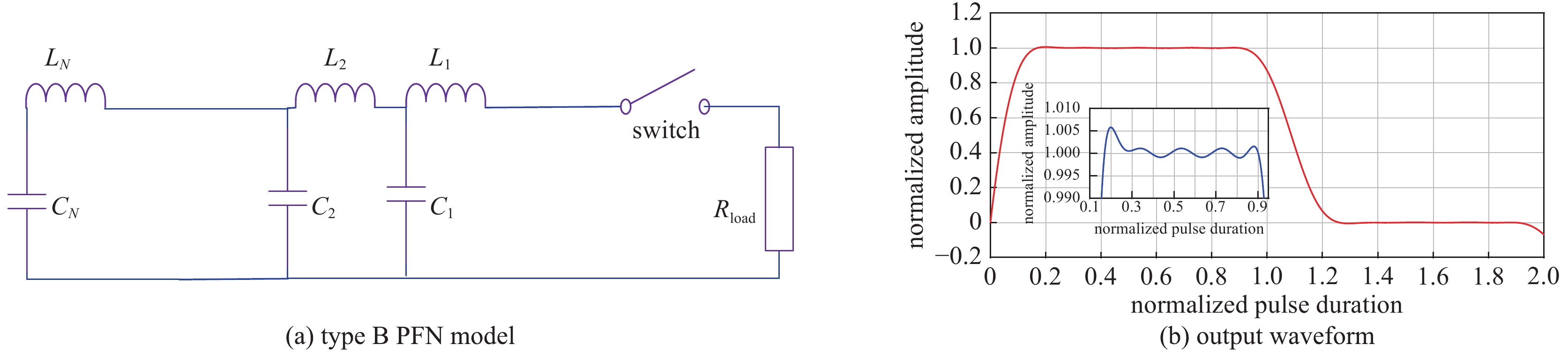
表 1 五节B型脉冲形成网络元件参数
Table 1. Parameters of devices in 5-stage B-type PFN
No. of stage L/μH C/μF 1 0.126 7 0.066 7 2 0.058 6 0.057 9 3 0.059 6 0.063 0 4 0.068 4 0.077 6 5 0.095 3 0.145 0 表 2 电容相等时邻近电感互耦的五节B型网路元件参数
Table 2. Parameters of devices in 5-stage B-type PFN with equal capacitors and adjacent mutual coupling inductors
coupling type C/μF L1/μH L2/μH L3/μH L4/μH L5/μH M1/μH M2/μH M3/μH M4/μH in-phase 0.098 378 0.149 565 0.075 587 0.073 823 0.076 589 0.087 982 0.007 871 0.012 273 0.011 811 0.009 485 out of phase 0.098 378 0.750 737 0.300 062 0.033 790 0.047 048 0.088 280 0.422 768 0.009 909 0.011 049 0.018 127 表 3 电容不等时邻近电感互耦的5节B型网路元件参数
Table 3. Parameters of devices in 5-stage B-type PFN with constrained capacitors and adjacent mutual coupling inductors
coupling type L1/μH L2/μH L3/μH L4/μH L5/μH M1/μH M2/μH M3/μH M4/μH in-phase 0.149 773 0.074 779 0.074 281 0.079 481 0.089 813 0.008 815 0.007 703 0.016 160 0.014 501 out of phase 0.740 300 0.295 738 0.034 265 0.044 260 0.091 035 0.415 044 0.012 123 0.009 084 0.013 038 -
[1] 李志强, 杨建华, 张建德, 等. 紧凑重频PFN-Marx脉冲发生器[J]. 强激光与粒子束, 2016, 28:015013. (Li Zhiqiang, Yang Jianhua, Zhang Jiande, et al. A compact repetitive PFN-Marx generator[J]. High Power Laser and Particle Beams, 2016, 28: 015013 doi: 10.11884/HPLPB201628.015013 [2] 黄华, 范植开, 马乔生, 等. 长脉冲相对论速调管放大器的初步实验研究[J]. 强激光与粒子束, 2002, 14(6):915-919. (Huang Hua, Fan Zhikai, Ma Qiaosheng, et al. Progress on a long pulse relativistic klystron amplifier[J]. High Power Laser and Particle Beams, 2002, 14(6): 915-919 [3] 田锦昌, 宋小泉, 李自良. HPM脉冲形成网络的理论分析与计算[J]. 飞行器测控学报, 2003, 22(3):72-74. (Tian Jinchang, Song Xiaoquan, Li Ziliang. Theoretical analysis and calculation of HPM pulse forming network[J]. Journal of Spacecraft TT&C Technology, 2003, 22(3): 72-74 [4] 吴谨, 万重怡. 紫外预电离TE(A) CO2激光器自持辉光放电的阻抗计算[J]. 激光杂志, 2002, 23(2):15-17. (Wu Jin, Wan Chongyi. Calculation of the glow discharge impedance of a UV-preionized self-sustained TE(A) CO2 laser[J]. Laser Journal, 2002, 23(2): 15-17 doi: 10.3969/j.issn.0253-2743.2002.02.005 [5] 刘锡三. 高功率脉冲技术[M]. 北京: 国防工业出版社, 2005: 116-119.Liu Xishan. High pulsed power technology. Beijing: National Defense Industry Press, 2005: 116-119 [6] 王传伟, 李洪涛. 基于互耦电感的两节准方波脉冲形成网络设计[J]. 强激光与粒子束, 2019, 31:040006. (Wang Chuanwei, Li Hongtao. Design of two-stage square pulse forming network with coupling inductors[J]. High Power Laser and Particle Beams, 2019, 31: 040006 doi: 10.11884/HPLPB201931.180299 [7] 潘子龙, 杨建华, 程新兵. 两节反谐振式网络输出方波脉冲的参数计算[J]. 强激光与粒子束, 2016, 28:045008. (Pan Zilong, Yang Jianhua, Cheng Xinbing. Parameter calculation of square pulse output in two-node anti-resonance network[J]. High Power Laser and Particle Beams, 2016, 28: 045008 doi: 10.11884/HPLPB201628.125008 [8] 王传伟, 李洪涛. 准方波脉冲形成网络的理论分析与设计[J]. 强激光与粒子束, 2018, 30:035005. (Wang Chuanwei, Li Hongtao. Theoretical analysis and design of the trapezoidal pulse forming network[J]. High Power Laser and Particle Beams, 2018, 30: 035005 doi: 10.11884/HPLPB201830.170392 [9] 谢政, 李建平, 陈挚. 非线性最优化理论与方法[M]. 北京: 高等教育出版社, 2010.Xie Zheng, Li Jianping, Chen Zhi. Nonlinear optimization theory and methods. Beijing: Higher Education Press, 2010 [10] 李春葆. 算法设计与分析[M]. 北京: 清华大学出版社, 2015.Li Chunbao. Algorithm design and analysis. Beijing: Tsinghua University Press, 2015 -




 下载:
下载: