Theory of optical-transition radiation and its application to pulsed electron beam diagnoses on linear induction electron accelerator
-
摘要:
匀速运动的带电粒子在穿过具有不同介电常数的两种媒质界面时要产生所谓光学渡越辐射。该辐射在粒子的入射平面上呈偏振行为;从辐射强度的角分布可以确定入射粒子的能量。在入射到双膜系统的情况下,由于干涉的发生,在第二膜前表面的强度角分布有振荡行为。利用这些现象,可对脉冲电子束包络半径、束电流密度的横向分布,束能量以及横向散角进行测量,依照这原理在各LIA加速器上进行的脉冲电子束参数测量,获得的有效数据极大地提高了加速器的调试效率。
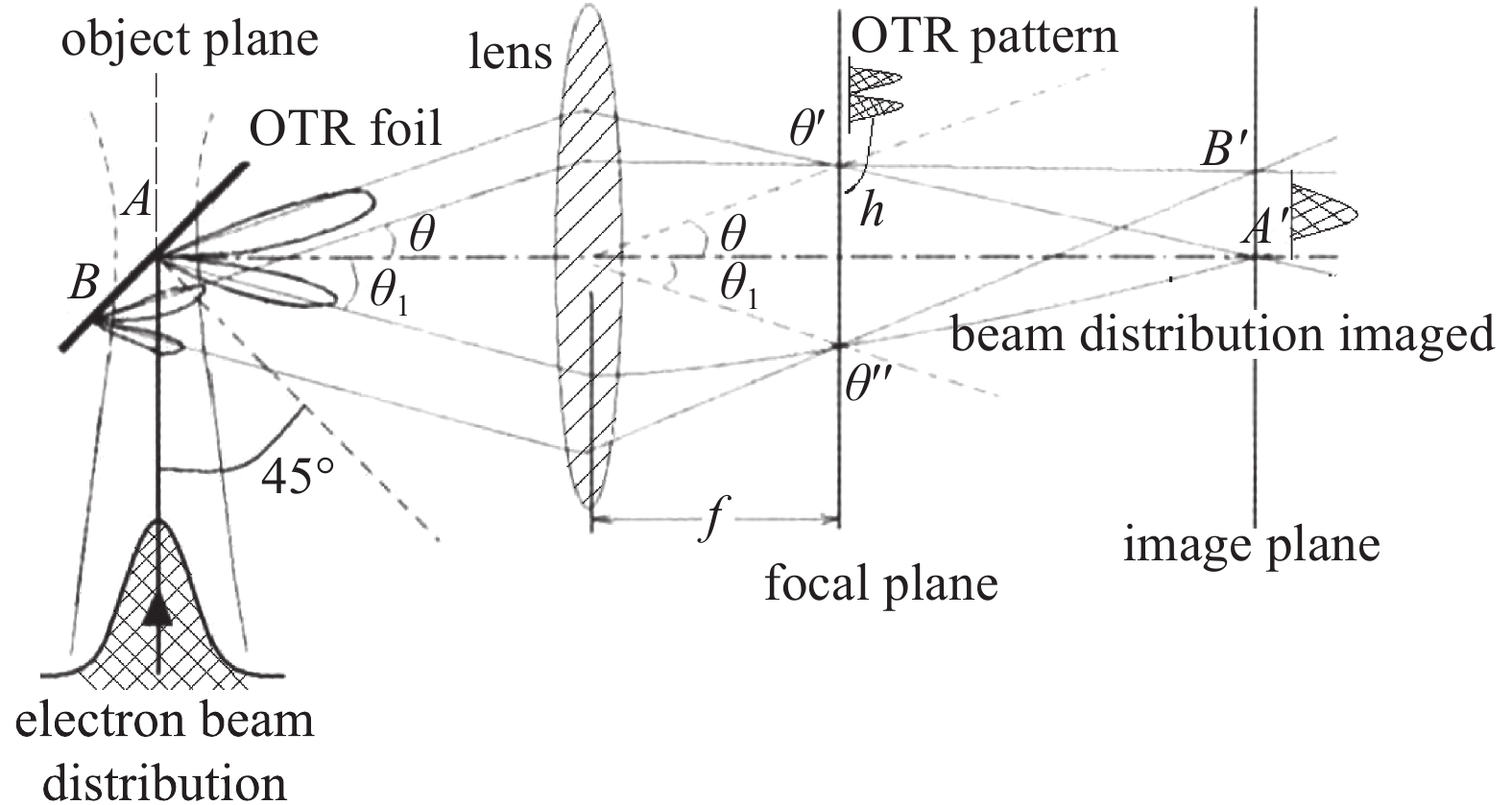
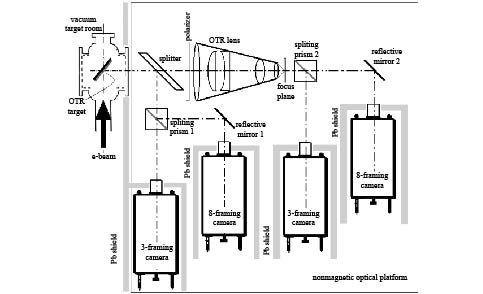
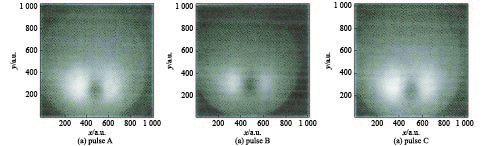
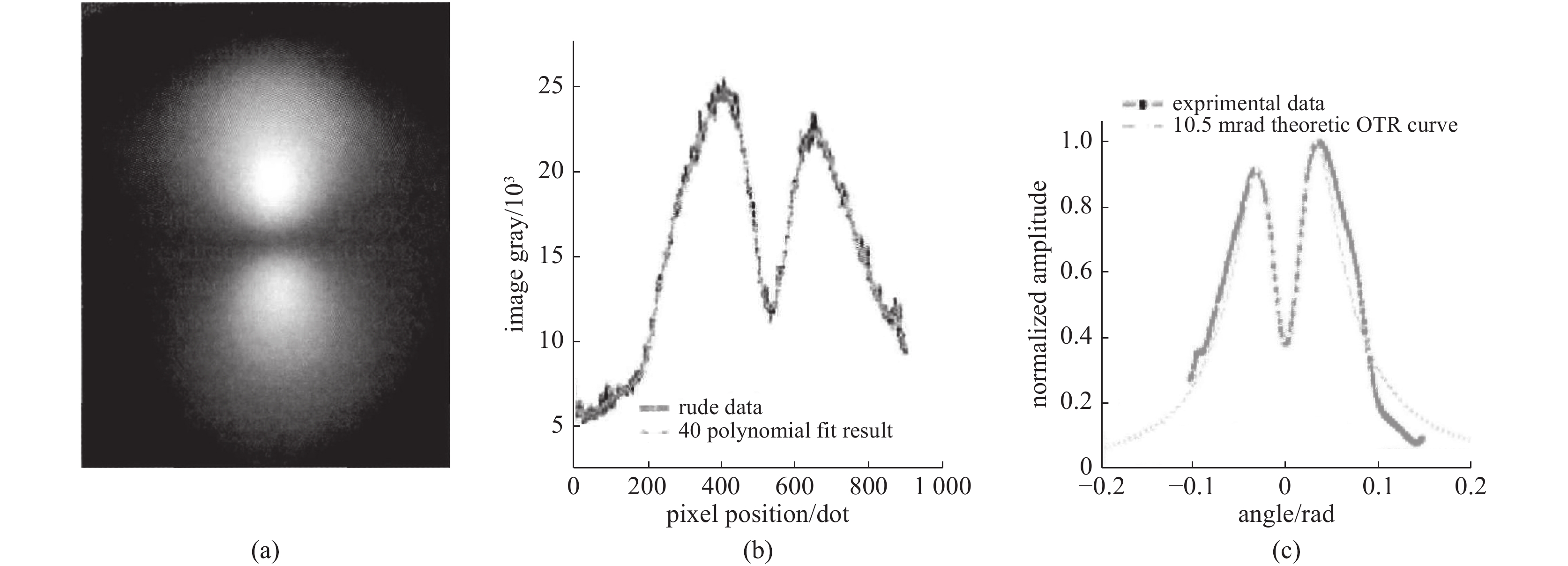
Abstract:It is can be bring optical-transition radiation(OTR) when the charged partical constant speed passed through interface of two dissimilarity intermedium. The radiation showed polarization behavior while the charged partical arrive at incidence plane, it is can be confirm energy of incidence partical corresponding OTR angle distribution patterns. The OTR angle distribution had polarization behavior at secondarily foil’s surface due to interference happened while electron beam entered the double foil system. It is can be measure parameter of pulse electron beam by used these phenomenon, The parameter includes electron beam envelope radius, landscape orientation distribution of electron beam current density, and electron beam energy, electron beam landscape orientation divergence angle distribution. using this theory to measure parameter of pulse electron beam basing on a series of Dragon LIAs and obtains valid time-resolved results. This measurement ability has improved greatly the debugging efficiency of a series of Dragon LIAs.
-
-
[1] Benford J, Swegle J A, Schamiloglu E. High power microwaes[M]. 3rd ed. London: Taylor & Francis Group, 2015. [2] Walter J W, Lynn C F, Dickens J C, et al. Operation of a sealed-tube-vircator high-power-microwave source[J]. IEEE Trans Plasma Science, 2012, 40(6): 1618-1621. doi: 10.1109/TPS.2012.2192454 [3] Mesyats G A. Cathode phenomena in a vacuum discharge: The breakdown, the spark and the Arc[M]. Moscow: Nauka, 2000. [4] Nunally W C. High-power microwave generation using optically activated semiconductor switches[J]. IEEE Trans Electron Devices, 1990, 37(12): 2439-2448. doi: 10.1109/16.64516 [5] Krasik Y E, Yarmolich D, Gleizer J Z, et al. Pulsed plasma electron sources[J]. Physics of Plasmas, 2009, 16(5): 7103. [6] Shiffler D, Haworth M, Cartwright K, et al. Review of cold cathode research at the Air Force Research Laboratory[J]. IEEE Trans Plasma Science, 2008, 36(3): 718-728. doi: 10.1109/TPS.2008.926227 [7] Levine J S, Harteneck B D. Repetitively pulsed relativistic klystron amplifier[J]. Applied Physics Letter, 1994, 65: 2133-2135. doi: 10.1063/1.112813 [8] 米勒R B. 强流带电粒子束物理导论[M]. 北京: 原子能出版社, 1990.Miller R B. Introduction to intense charged-particle beam physics[M]. Beijing: Atomic Energy Press, 1990 [9] Wang Yuan, Jiang Xiaoguo, Yang Guojun, et al. Time-resolved energy spectrum measurement of a linear induction accelerator with the magnetic analyzer[J]. Chinese Physics C, 2015, 39: 017004. doi: 10.1088/1674-1137/39/1/017004 [10] 戴光森, 刘承俊, 丁伯南, 等. 10 MeV LIA加速电压、电子束流测试[J]. 强激光与粒子束, 1996, 8(5):187-192. (Dai Guangsen, Liu Chengjun, Ding Bonan, et al. Voltage pulse and electron beam current measurement on the 10 MeV LIA[J]. High Power Laser and Particle Beams, 1996, 8(5): 187-192 [11] 石金水, 丁伯南, 邓建军, 等. 12 MeV直线感应电子加速器[J]. 强激光与粒子束, 1997, 9(4):599-604. (Shi Jinshui, Ding Bonan, Deng Jianjun, et al. 12 Mev linear induction electron accelerator[J]. High Power Laser and Particle Beams, 1997, 9(4): 599-604 [12] 丁伯南, 邓建军, 王华岑, 等. “神龙一号”直线感应电子加速器[J]. 高能物理与核物理, 2005, 29(6):604-610. (Ding Bonan, Deng Jianjun, Wang Huacen, et al. DragonⅠ linear induction electron accelerator[J]. High Energy Physics and Nuclear Physics, 2005, 29(6): 604-610 doi: 10.3321/j.issn:0254-3052.2005.06.015 [13] 石金水, 邓建军, 章林文, 等. 神龙二号加速器及其关键技术[J]. 强激光与粒子束, 2016, 28:010201. (Shi Jinshui, Deng Jianjun, Zheng Linwen, et al. Dragon-II accelerator and its key technology[J]. High Power Laser and Particle Beams, 2016, 28: 010201 doi: 10.11884/HPLPB201628.010201 [14] 江孝国, 王远, 杨国君, 等. 时间分辨的强流脉冲电子束参数的光学测量诊断系统研制[J]. 强激光与粒子束, 2013, 25(11):2780-2784. (Jiang Xiaoguo, Wang Yuan, Yang Guojun, te al. Development of time-resolved optical measurement and diagnostic system for parameters of high current and pulsed electron beam[J]. High Power Laser and Particle Beams, 2013, 25(11): 2780-2784 doi: 10.3788/HPLPB20132511.2780 [15] Jiang Xiaoguo, Wang Yuan, Zhang Kaizhi, et al. Instantaneous electron beam emittance measurement system based on the optical transition radiation principle[J]. Chinese Physics C, 2014, 38: 017002. doi: 10.1088/1674-1137/38/1/017002 [16] Jiang Xiaoguo, Wang Yuan, Yang Zhiyong, et al. Time-resolved measurement technique for pulsed electron beam envelope basing on framing and streaking principle[J]. Chinese Physics C, 2016, 40: 017003. doi: 10.1088/1674-1137/40/1/017003 -





 下载:
下载: