Simulation study on measurement characteristics of ion energy analyzer
-
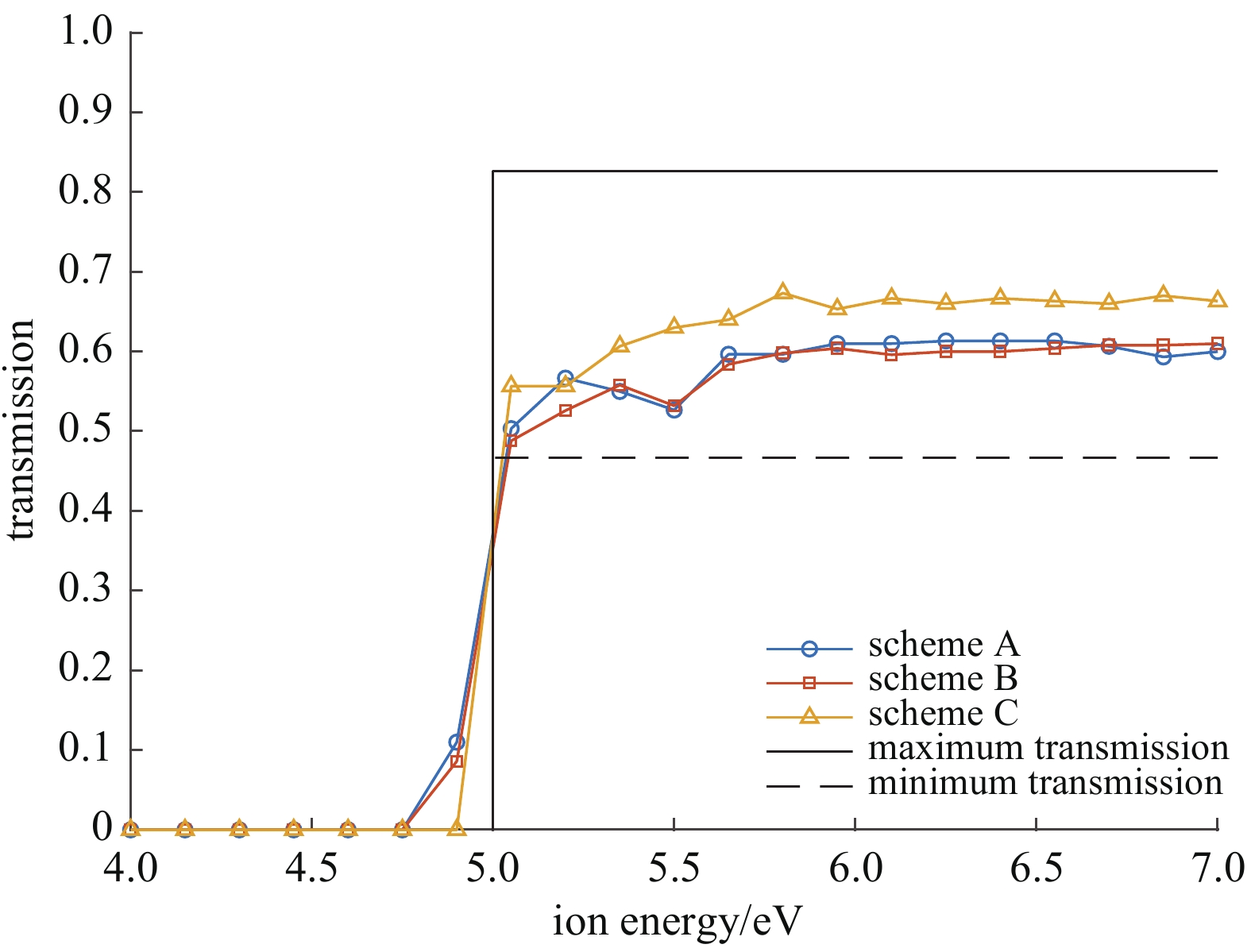
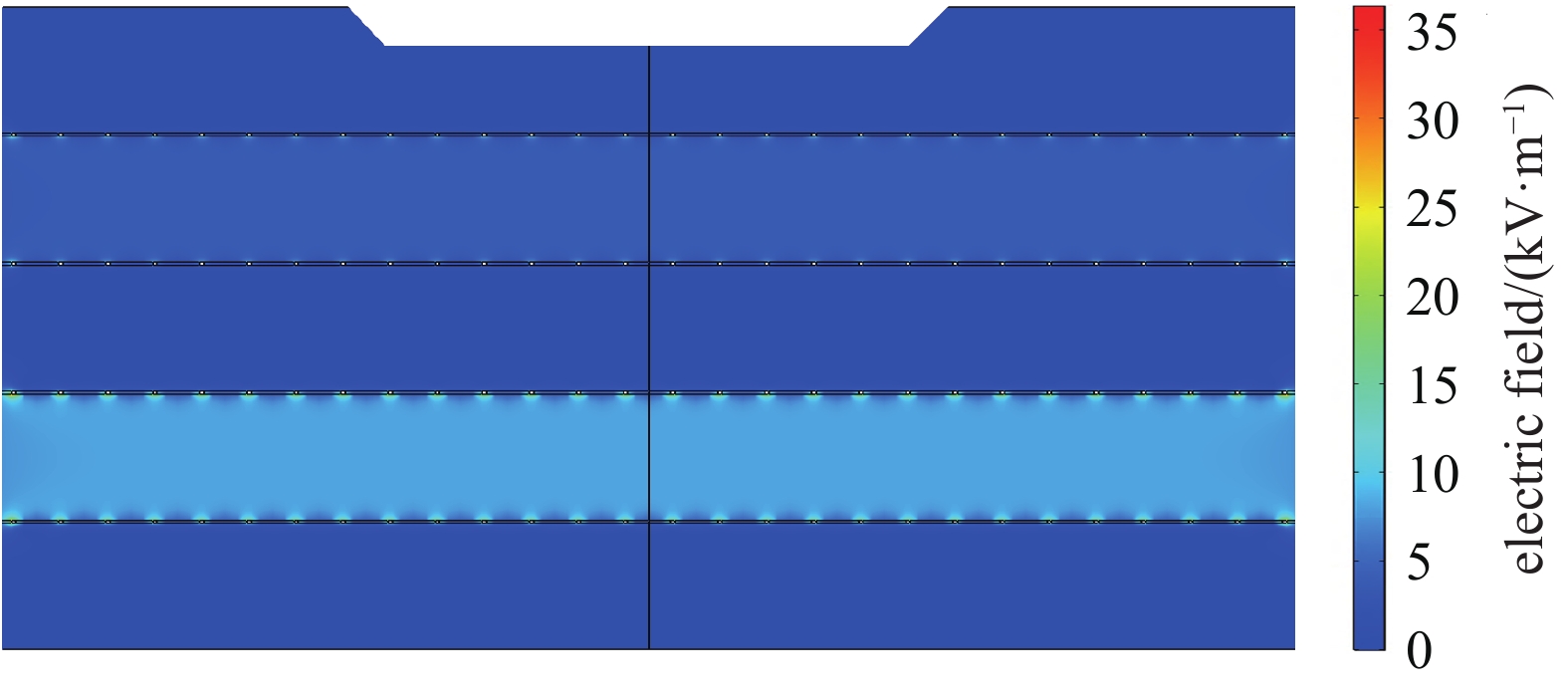
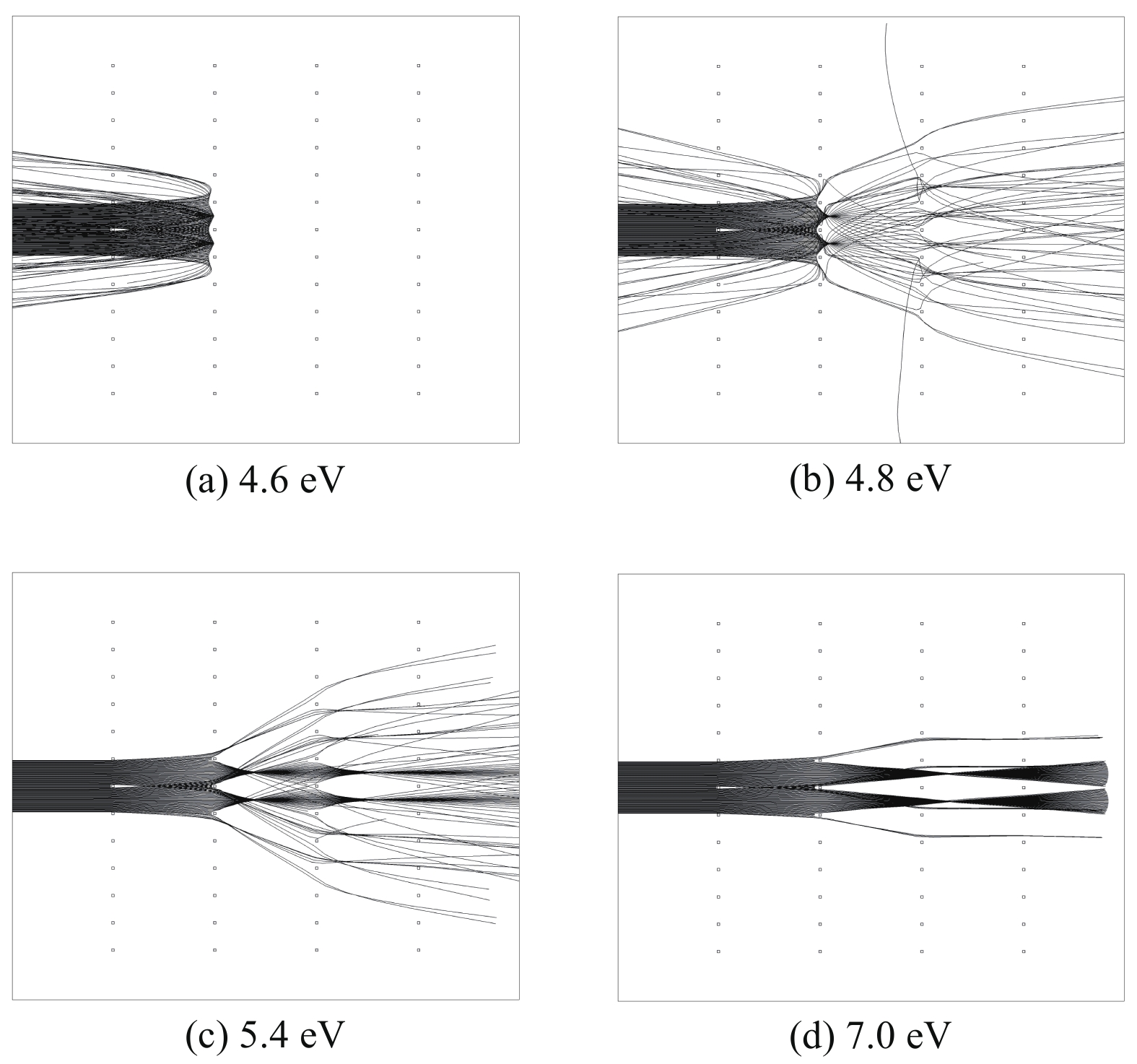
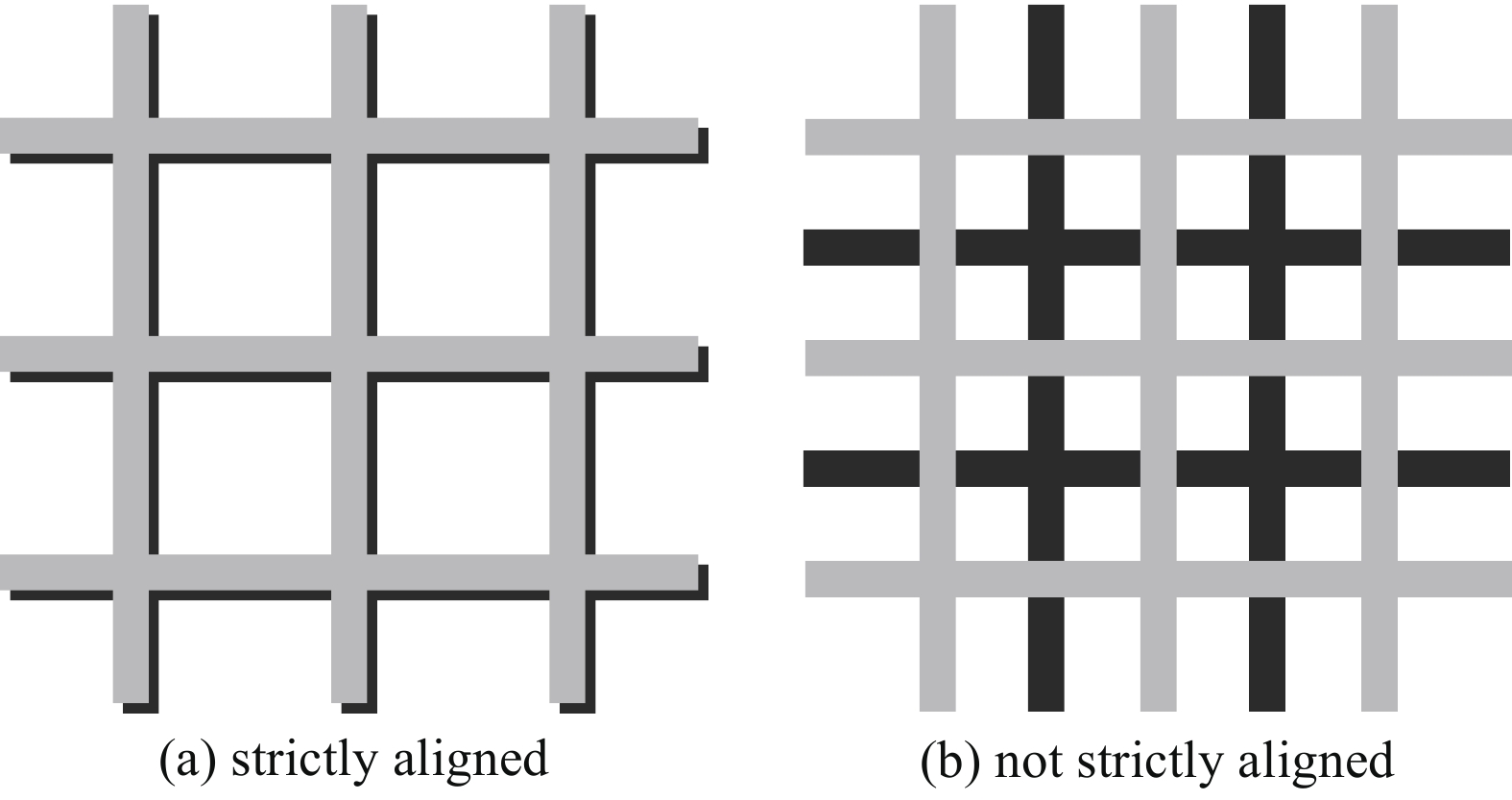
摘要: 针对空间等离子体及其模拟环境、空间原子氧及其模拟环境对离子能谱测量的需要,利用仿真软件COMSOL,对离子能量分析器的低能离子测量特性进行了仿真研究。介绍了离子能量分析器的工作原理,对离子能谱测量过程进行了公式推导。通过对三种待选仪器设计方案进行离子透过率仿真分析,确定了一种较优的仪器设计方案。多种离子温度下的误差分析结果也表明,该设计方案能够较为准确地测量离子能量分布。分析了电场畸变、等离子鞘层、栅网对齐方式和离子温度对测量结果的影响,根据仿真结果对一些仿真实验现象做出了合理的解释。Abstract: The ion energy analyzer (IEA), also known as the retarding potential analyzer (RPA), is widely used as an important tool for measuring plasma energy in situ and is widely used in ionospheric detection satellites. The ion energy of the ionosphere is too low to be stabilized, thus the measurement characteristics of the IEA can’t be effectively studied through experiments. As there is no such problem in simulation, simulation has become a powerful tool for studying IEA. This paper analyzes the low-energy ion measurement characteristics of the IEA through the simulation software COMSOL, introduces the working principle of the IEA, and gives a comprehensive formula derivation for the ion measurement process. Based on simulation and analysis of three candidate design schemes, one of the schemes whose transmission curve is closest to the ideal step function is chosen. In theory, the measurement results of this scheme have the least error. The comprehensive error analysis results at various ion temperatures also show that the gap between the measurement results and the theoretical value of the scheme is narrow. The ion energy distribution can be measured more accurately. Finally, the effects of electric field distortion, plasma sheath, grid alignment and ion temperature are studied. According to these simulations, some experimental phenomena can be reasonably explained.
-
表 1 不同温度下离子速度拟合结果
Table 1. Ion velocity fitting results at different temperatures
temperature/K average velocity/(m·s−1) relative error/% ${\varepsilon _{\rm{RMSE}}}$/eV 500 7593 −0.09 0.05 1000 7626 0.34 0.11 1500 7657 0.75 0.07 2000 7811 2.77 0.73 -
[1] Bourdeau R E, Whipple E C Jr, Donley J L, et al. Experimental evidence for the presence of helium ions based on Explorer VIII satellite data[J]. Journal of Geophysical Research, 1962, 67(2): 467-475. doi: 10.1029/JZ067i002p00467 [2] Sarkar S, Gwal A K, Parrot M. Ionospheric variations observed by the DEMETER satellite in the mid-latitude region during strong earthquakes[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2007, 69(13): 1524-40. doi: 10.1016/j.jastp.2007.06.006 [3] 陳信良. 中華衛星一號電離層電漿電動效應儀 (IPEI) 資料之頻譜分析[D]. 台灣: 國立中央大學, 2009: 4-7.Chen Hsinliang. Spectrum analysis of the data of China Satellite No. 1 Ionospheric Plasma and Electrodynamics Instrument (IPEI)[D]. Taiwan: National Central University, 2009: 4-7 [4] Sgrigna V, Buzzi A, Conti L, et al. The ESPERIA satellite project for detecting seismo-associated effects in the topside ionosphere: First instrumental tests in space[J]. Earth Planets Space, 2008, 60(5): 463-475. doi: 10.1186/BF03352813 [5] Satir M, Sik F, Turkoz E, et al. Design of the retarding potential analyzer to be used with BURFIT-80 ion thruster and validation using PIC-DSMC code[C]/7th International Conference on Recent Advances in Space Technologies. 2015. [6] Goldan P D, Yadlowsky E J, Whipple E C. Errors in ion and electron-temperature measurements due to grid plane potential nonuniformities in retarding potential analyzers[J]. Journal of Geophysical Research, 1973, 78(16): 2907-2916. doi: 10.1029/JA078i016p02907 [7] Troy B E, Maier E J. Effect of grid transparency and finite collector size on determining ion temperature and density by retarding potential analyzer[J]. Journal of Geophysical Research−Space Physics, 1975, 80(16): 2236-2240. doi: 10.1029/JA080i016p02236 [8] Knudsen W C. Finite grid radius and thickness effects on retarding potential analyzer measured suprathermal electron-density and temperature[J]. Journal of Geophysical Research−Space Physics, 1992, 97(A9): 13767-13775. doi: 10.1029/92JA00642 [9] Chao C K, Su S Y. Charged particle motion inside the retarding potential analyzer[J]. Physics of Plasmas, 2000, 7(1): 101-107. doi: 10.1063/1.873817 [10] Chao C K, Su S Y, Yeh H C. Grid effects on the derived ion temperature and ram velocity from the simulated results of the retarding potential analyzer data[J]. Advances in Space Research, 2003, 32(11): 2361-2366. doi: 10.1016/S0273-1177(03)90566-7 [11] Klenzing J H, Earle G D, Heelis R A, et al. A statistical analysis of systematic errors in temperature and ram velocity estimates from satellite-borne retarding potential analyzers[J]. Physics of Plasmas, 2009, 16: 052901. doi: 10.1063/1.3125311 [12] 冯宇波, 王世金, 孔令高. 电离层星载阻滞势分析器的误差仿真分析[J]. 地球物理学报, 2010, 53(11):2535-2543. (FengYubo, Wang Shijin, Kong Linggao. Simulation analysis of errors from ionosphere satellite-borne retarding potential analyzer[J]. Chinese Journal of Geophysics−Chinese Edition, 2010, 53(11): 2535-2543 [13] Fisher L E, Lynch K A, Fernandes P A, et al. Including sheath effects in the interpretation of planar retarding potential analyzer’s low-energy ion data[J]. Review of Scientific Instruments, 2016, 87: 043504. doi: 10.1063/1.4944416 [14] Pfaff F, Borovsky E, Young T. Measurements of thermal ion drift velocity and temperature using planar sensors[J]. Geophysical Monograph, 1998, 102: 61-71. [15] COMSOL Inc. Particle tracing module updates[EB/OL]. https://www.comsol.com/release/5.3/particle-tracing-module. [16] Bilitza D, Altadill D, Reinisch B, et al. The international reference ionosphere: model update 2016[C]//EGU General Assembly Conference Abstracts. 2016: 18. [17] The Community Coordinated Modeling Center. International Reference Ionosphere−IRI (2016) with IGRF-13 coefficients [EB/OL]. https://ccmc.gsfc.nasa.gov/modelweb/models/iri2016_vitmo.php. [18] Marrese C M, Majumdar N, Haas J, et al. Development of a single-orifice retarding potential analyzer for Hall thruster plume characterization[C]//25th International Electric Propulsion Conference. 1997: 397-404. [19] Zheng Xiangzhi, Zhang Aibing, Guan Yibing, et al. Research on retarding potential analyzer aboard China seismo-electromagnetic satellite[J]. Acta PhysicaSinica, 2017, 66: 079401. [20] 熊年禄, 唐存琛, 李行健. 电离层物理概论[M]. 武汉: 武汉大学出版社, 1999: 53-55.Xiong Nianlu, Tang Chunshen, Li Xingjian. Introduction to ionospheric physics[M]. Wuhan: Wuhan University Press, 1999: 53-55 [21] Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing[M]. New Jersey: John Wiley & Sons, 2005. -




 下载:
下载: