Stripping effect of hydrogen atom beam in long-range atmospheric propagation
-
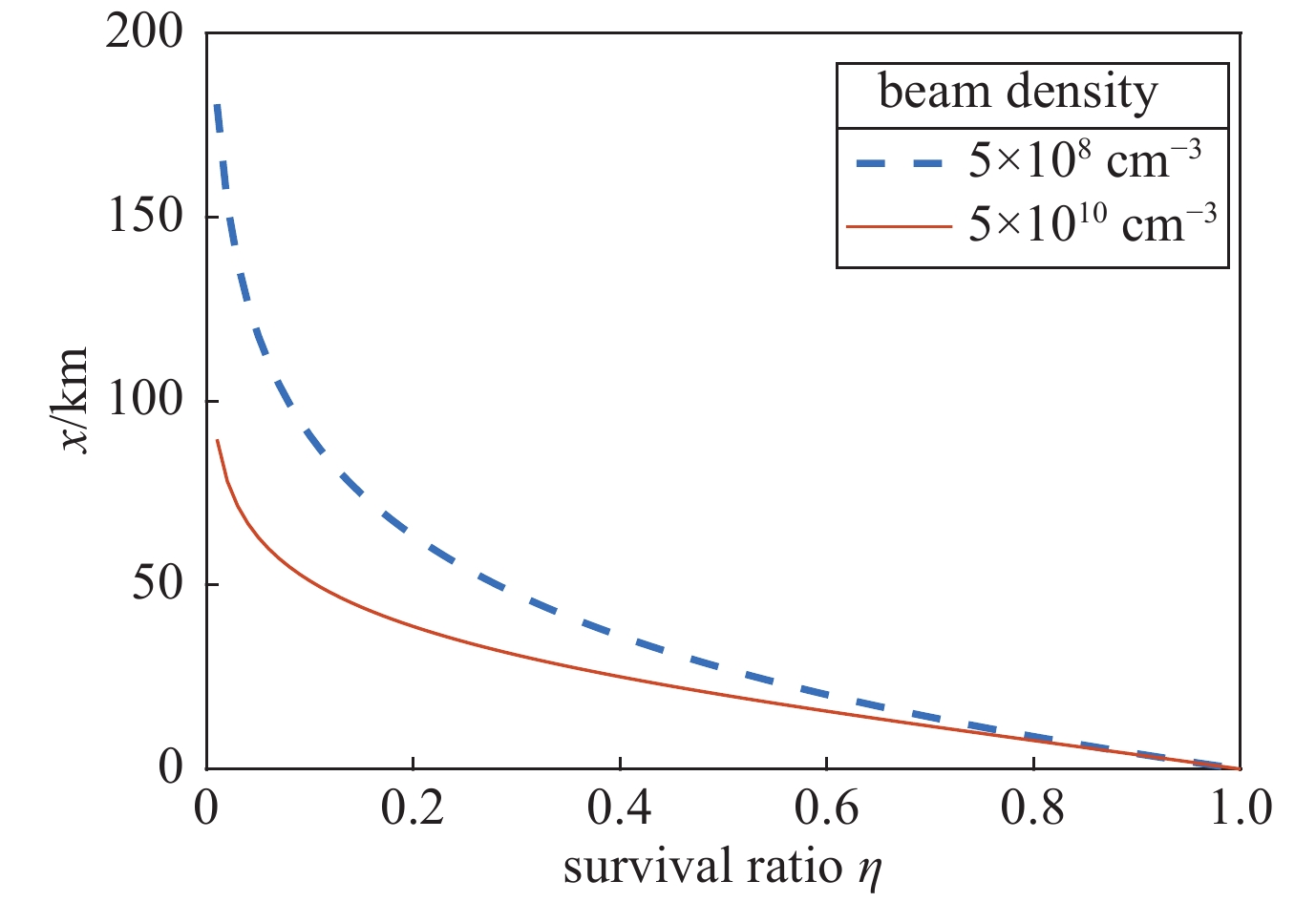
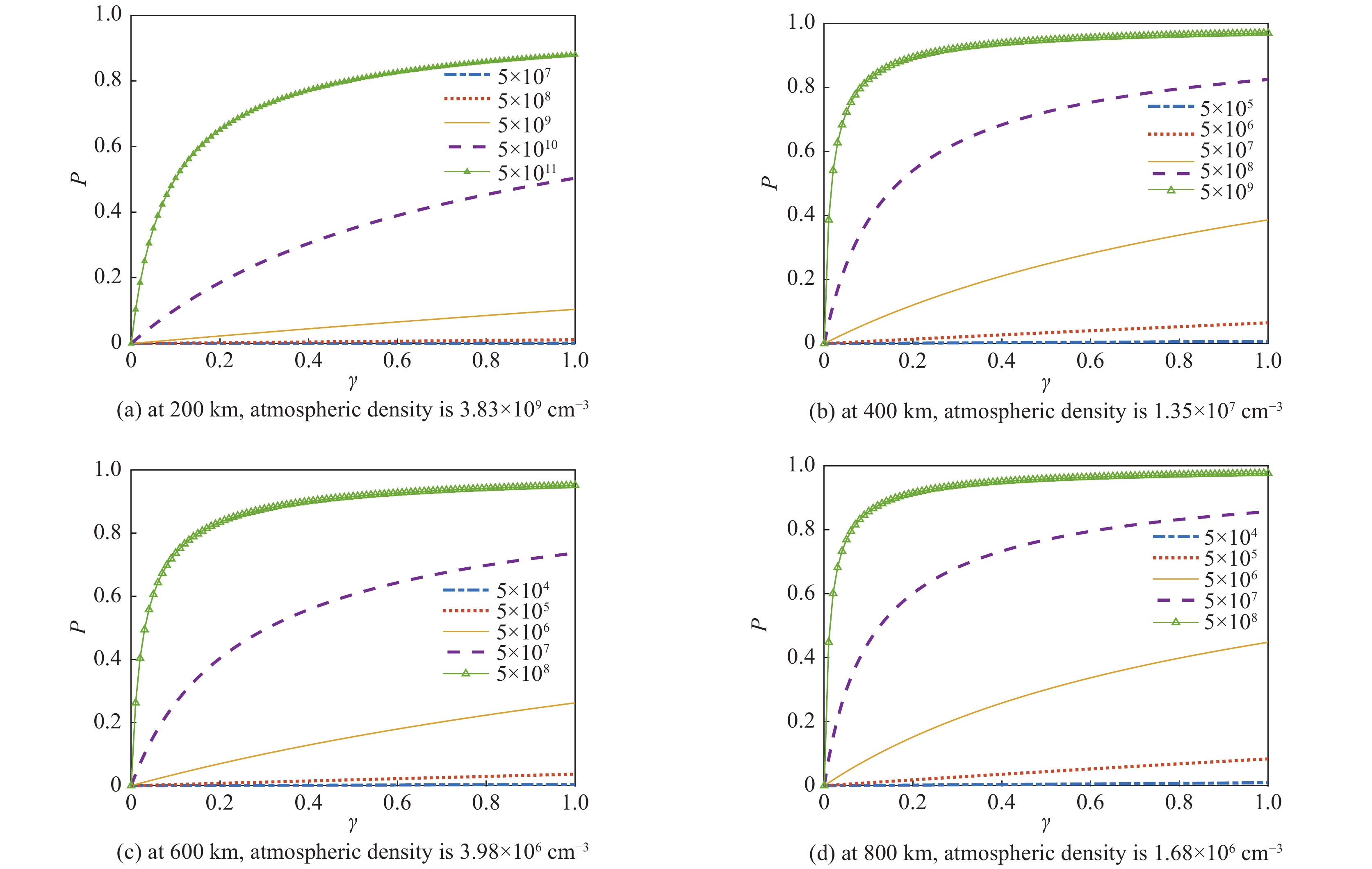
摘要: 考虑到中性粒子束对近地轨道太空垃圾的清理作用以及在太空探索中的潜在应用前景,研究了中性粒子束在亚轨道空间长程传输过程中影响束流能量和密度损失的主要物理机制,重点分析了剥离效应对束流损耗的影响。中性束剥离效应包括束流粒子之间碰撞导致的自剥离效应和其与大气粒子碰撞导致的剥离效应。以束密度随传播距离变化的方程为基础,通过引用几何因子来表征束流的自剥离效应强度,建立了剥离效应机制下束流的传输模型,由此评估了束流自剥离效应在中性束长程传输中对传输距离的影响关系。研究结果表明,在固定的高度,当中性束密度大于空气粒子密度时,自剥离效应的影响将非常突出,随着传输高度的升高,即使束密度和空气密度同时降低维持量级一致,自剥离效应对传输距离的影响在大几何因子的情况下仍会增强。Abstract: Considering the neutral particle beams can help cleaning effect in space debris in low-Earth orbit and their potential application prospects in space exploration, this paper analyzes several major mechanisms that cause beam energy loss and density loss during the long-range transmission of neutral particle beams in sub-orbital space, and focuses on analyzing the effect of stripping effects on beam loss. The neutral beam stripping effects include self-stripping effects caused by collisions of stripped particles with beam particles and stripping effects caused by collisions of beam particles with atmospheric particles. Based on the equation that the beam density changes with the propagation distance, this paper introduces a geometric factor to characterize the intensity of the self-stripping effect of the beam, and derives the functional relationship between the transmission distance and the geometric factor. By normalizing the transmission distance under a certain particle survival ratio, it evaluates the relative importance of the effect of beam self-stripping on the transmission distance in the long-range transmission of neutral beams. The results show that at a fixed height, when the neutral beam density is greater than the density of air particles, the self-stripping effect will be very strong. With the increase of the transmission height, even if the beam density and the air density decrease at the same time with the same order of magnitude, the effect of self stripping on the transmission distance will increase with a large geometric factor.
-
Key words:
- neutral beam /
- long-range transmission /
- stripping-effect /
- sub-orbital
-
表 1 大气粒子主要成分电离截面参数
Table 1. Ionization cross section parameters of main components of atmospheric particles
σi/cm2 i=1 i=2 i=3 i=4 i=5 N2 O2 He Ar charged particle 0.628×10−16 1.084×10−16 0.137×10−16 0.650×10−16 2.000×10−16 表 2 描述自剥离效应的主要参数
Table 2. Main parameters to describe self-stripping effect
j X γj σj/cm2 nj/cm−3 1 e γ 0.9×10−18 N-b 2 H+ γ 0.135×10−16 N-b -
[1] Li Bin, Sang Jizhang. Efficient and accurate error propagation in the semi-analytic orbit dynamics system for space debris[J]. Advances in Space Research, 2020, 65(1): 285-296. doi: 10.1016/j.asr.2019.09.016 [2] Carmen P, Luciano A. Environmental sustainability of large satellite constellations in low earth orbit[J]. Acta Astronautica, 2020, 170: 27-36. doi: 10.1016/j.actaastro.2020.01.016 [3] Cordelli E, Vananti A, Schildknecht T. Analysis of laser ranges and angular measurements data fusion for space debris orbit determination[J]. Advances in Space Research, 2020, 65(1): 419-434. doi: 10.1016/j.asr.2019.11.009 [4] Hossein S H, Acernese M, Cardona T, et al. Sapienza Space debris Observatory Network (SSON): A high coverage infrastructure for space debris monitoring[J]. The Journal of Space Safety Engineering, 2020, 7(1): 30-37. doi: 10.1016/j.jsse.2019.11.001 [5] Lacruz E, Casanova D, Abad A. Estimation of a reliability range for the area-to-mass ratio of orbiters at the geostationary ring[J]. Acta Astronautica, 2020, 166: 104-112. doi: 10.1016/j.actaastro.2019.09.039 [6] Riel T, Sinn A, Schwaer C, et al. Iterative trajectory learning for highly accurate optical satellite tracking systems[J]. Acta Astronautica, 2019, 164: 121-129. doi: 10.1016/j.actaastro.2019.07.012 [7] Zhao Sisi, Michael S, Georg K, et al. Attitude analysis of space debris using SLR and light curve data measured with single-photon detector[J]. Advances in Space Research, 2020, 65(5): 1518-1527. doi: 10.1016/j.asr.2019.12.005 [8] Carini P, Kalman G, Pulsifer P. Neutral beam propagation effects in the upper atmosphere[R]. AFGL-TR-85-0038, 1985: 11-24. [9] Lai ST. Ionization of a high energy neutral beam propagating in the ionosphere[C]//1992 9th International Conference on High-Power Particle Beams. 1992: 1907-1911. [10] Neumann H, Le T Q, Zyl B V. H+Ar collisions. II. Differential scattering calculations[J]. Phys Rev A, 1978, 15(5): 1887-1892. [11] Zyl B V, Neumann H, Le T Q, et al. H+N2 and H+O2 collisions: Experimental charge-production cross sections and differential scattering calculations[J]. Phys Rev A, 1978, 18(2): 506-516. doi: 10.1103/PhysRevA.18.506 -




 下载:
下载: